嫦娥四号着陆器月面定时定点着陆轨道控制策略设计与实施

刘德成 周文艳 高珊 李飞 杨眉

(北京空间飞行器总体设计部，北京 100094)

嫦娥三号探测器的目标着陆区为虹湾地区，整个区域面积广大，地势均较为平坦，因此可以选一个面积较大的预定着陆区域，对于不同的发射日期和转移轨道，即便存在一定的轨道飞行控制误差，总可以找到满足任务要求的着陆点，因此没有定点着陆的需求。嫦娥四号探测器任务目标为着陆月球背面。相对于月球正面，背面地形更加崎岖复杂，大量的撞击盆地密布，难以找到大片的平坦区域，由此提出了定点着陆的要求[1-3]。另一方面，动力下降前的测控弧段也是必须保证的条件，而测控弧段与着陆时刻直接相关，因此又对嫦娥四号着陆器提出了定时着陆的要求。

根据着陆任务的飞行过程，定点着陆常用的变轨策略主要是圈次调整、调相轨道和轨道面调整等[4-6]。文献[7]以月面定点采样返回任务为背景，根据采样返回任务的飞行时序和测控条件约束分析了月球倾斜轨道的定点采样变轨策略，采用一个2对2的机动瞄准目标动力下降起始点高度和着陆点纬度，通过轨道平面调整机动瞄准目标着陆点纬度，但该策略未对着陆点时刻进行约束。本文根据嫦娥四号的任务约束，在考虑测控要求、环月倾角接近90°的条件下，以满足嫦娥四号任务需求为目标，提出了一种基于双层迭代的高精度“定时定点”月面软着陆轨道控制策略，然后针对飞控中各种因素的残差，在近月制动和环月修正增加面外修正速度增量，确保落点位置和时刻的精度满足要求。

1 单层迭代的轨道控制策略

嫦娥三号软着陆任务的着陆区为月球正面的虹湾，由于虹湾地区相对而言较为平坦，可着陆区域较大，任务计划的着陆区域为：月面纬度44.1°N±1.5°N，经度18.2°W～34.6°W。

着陆区域经度方向范围宽达16.3°，月球每天自转13.2°，因此对于倾角为90°的环月轨道，通过调整环月飞行时间即可保证探测器落在指定区域内，对于着陆器并不存在定时定点着陆的要求。

嫦娥三号的飞行过程以及轨道控制策略如图1所示，整个飞行过程由地月转移段、环月飞行段和动力下降段组成。嫦娥四号着陆器的主要飞行过程与嫦娥三号类似[8]。本文不考虑动力下降段误差对着陆点的影响，重点阐述的是通过对地月转移段和环月飞行段的轨道控制策略设计，使得着陆器在动力下降初始点预报的着陆点满足任务要求。

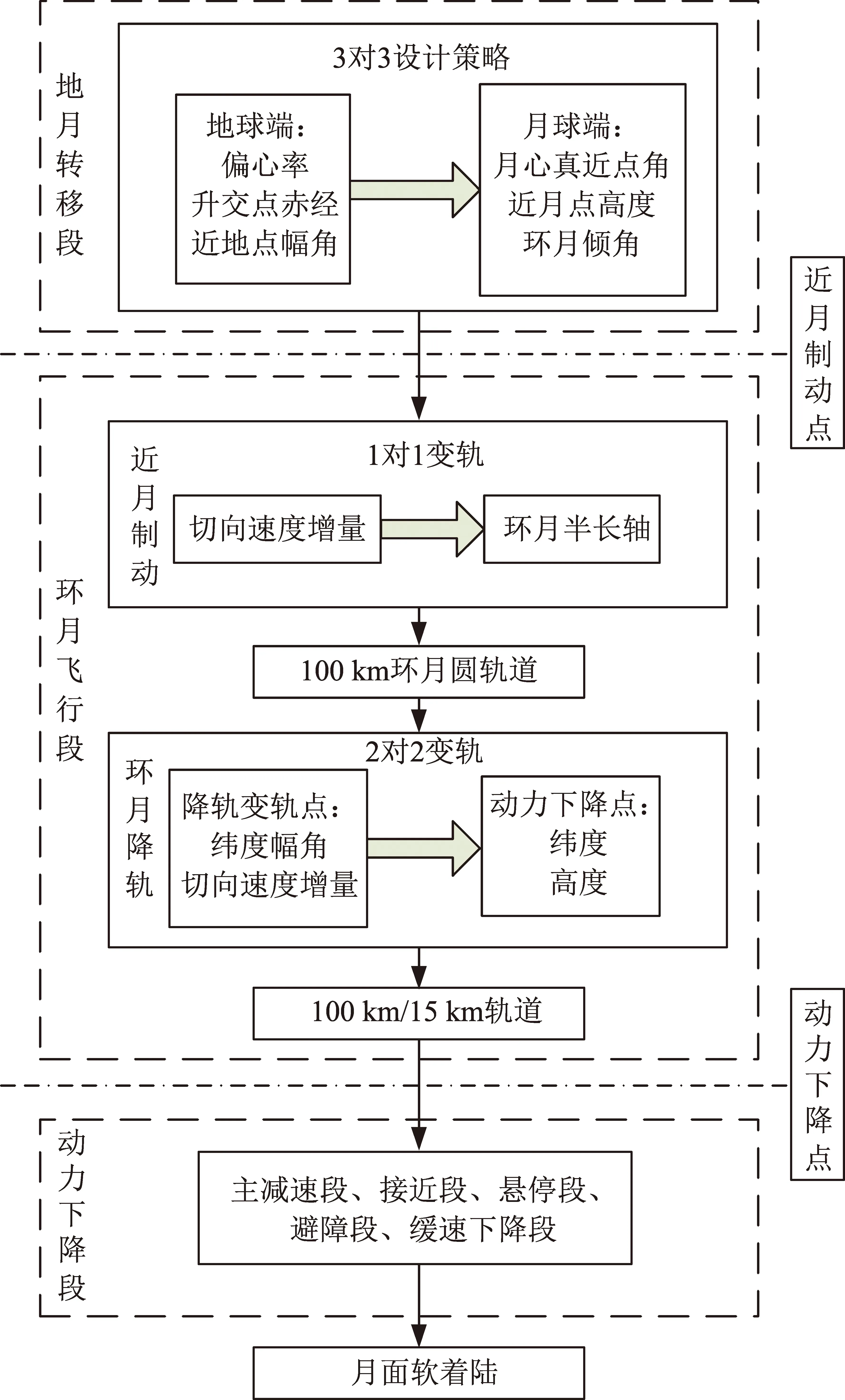
图1 嫦娥三号探测器飞行过程及轨道控制策略

图1中，“3对3设计策略”、“1对1变轨”中前面的数字为设计变量的个数，后面的数字为目标变量的个数，采用微分修正方法迭代设计变量满足目标变量的要求，令q为目标变量，p为设计变量，则目标变量和设计变量之间的关系可以表示为[9]

q=q(p)

(1)

猜测一个初值p0，则q0=q(p0)，得到Δq=qT-q0，其中qT为目标值。

两者之间的误差关系可线性化表示为

(2)

p=p0+Δp

(3)

通过若干次迭代，就可以使得Δq满足允许误差，这是求解微分方程常用的方法。

在地月转移段中

(4)

(5)

式中：v0为近地点速度；Ω为升交点赤经；ω为近地点角距；Hm为近月点高度；k为月心赤道惯性坐标系z轴方向的单位矢量；r1，v1是月心惯性系中近月点的位置与速度。由q2和q3的表达式可知：q2表示探测器在近月点时相对于月球的速度和月心矢径的夹角的余弦，q3表示探测器在近月点时相对于月球赤道面的瞬时轨道倾角。

在近月制动时

(6)

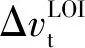
在环月降轨时

(7)

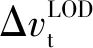
根据图1的轨道方案进行计算，各发射窗口标称轨道参数如表1所示。

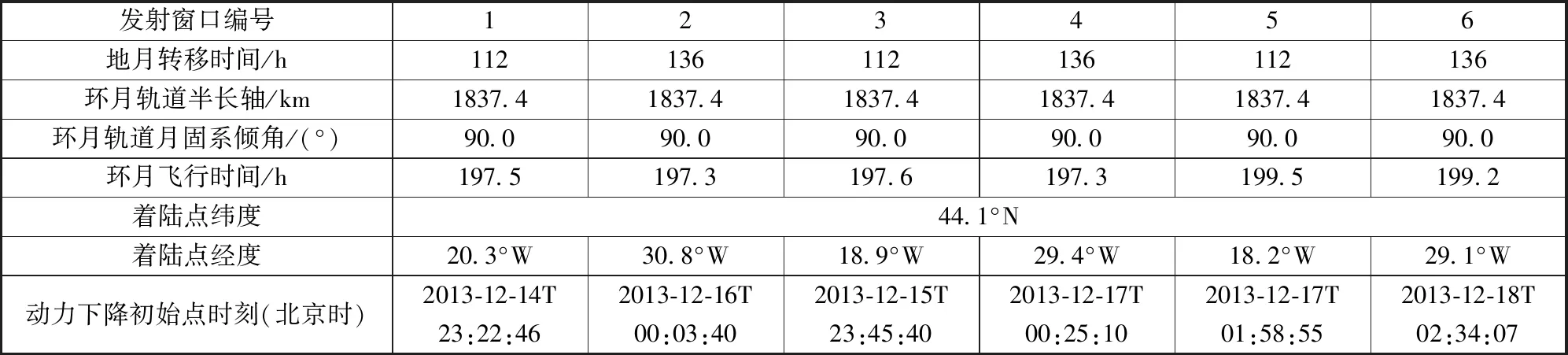
表1 嫦娥三号探测器标称轨道参数

由以上结果可知，每一个发射窗口的标称环月轨道半长轴和倾角相同，但动力下降初始点时刻及对应的标称落点各不相同，112 h转移时间轨道的标称落点集中在20°W附近，136 h转移时间轨道的标称落点集中在30°W附近。

2 双层迭代定时定点着陆轨道控制策略

嫦娥四号预定主着陆区为月面经度177.6°E±1.2°E，月面纬度45.5°S±0.5°S，着陆范围仅有嫦娥三号着陆区范围的5%，图2等比例给出了嫦娥三号与嫦娥四号着陆的目标着陆区。

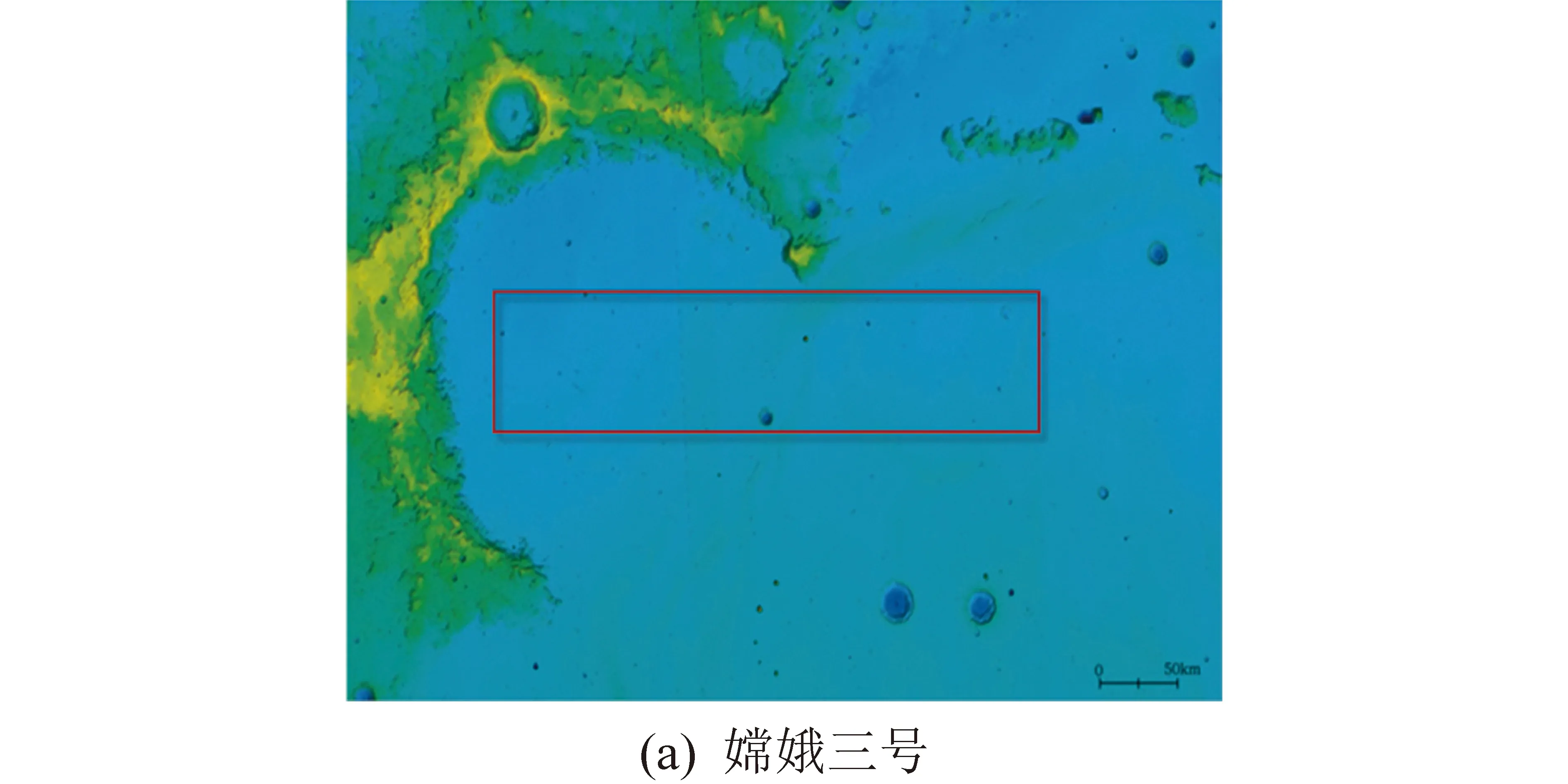
图2 嫦娥三号与嫦娥四号目标着陆区域

受动力下降段GNC系统制导律的约束，着陆器在动力下降段不具备着陆点位置的调整能力，因此动力下降初始点(自由飞行轨道与动力下降段的衔接点)的位置才是决定着陆点位置的重要因素。考虑到着陆器动力下降过程存在着陆点误差，并留取一定余量，因此任务要求轨道控制残差带来的落点经度(落点纬度误差通过微调动力下降点时刻保证)精度要求小于0.1°；地面测控站对着陆器的可见性又限定了着陆时刻，任务中要求着陆时刻误差小于1 min。针对这一问题，设计了一种基于双层迭代的高精度“定时定点”月面软着陆轨道控制策略，通过近月制动和环月修正多次应用该轨道控制策略，逐次缩小轨道控制残差，满足着陆区范围缩小带来的动力下降初始点的位置和时刻精确瞄准的需求。

该轨道控制策略主要包括两层迭代(流程如图3所示)：①外层迭代为“2对2”的轨道控制策略，设计变量为环月变轨(包括近月制动和环月修正)速度增量的切向和法向控制量，目标为动力下降初始点时刻与着陆点经度；②内层迭代包含另一个“2对2”的轨道控制策略，设计变量为环月降轨时刻及变轨速度增量，目标为动力下降点高度和纬度。

在实际飞控实施中，当已完成近月制动和环月修正，需要进行环月降轨策略计算时，增加环月降轨变轨速度增量法向控制量为设计变量来瞄准着陆点经度，形成“3对3”的轨道控制策略，即设计变量为环月降轨时刻、变轨速度增量切向和法向控制量，控制目标为动力下降点高度、纬度和着陆点经度。

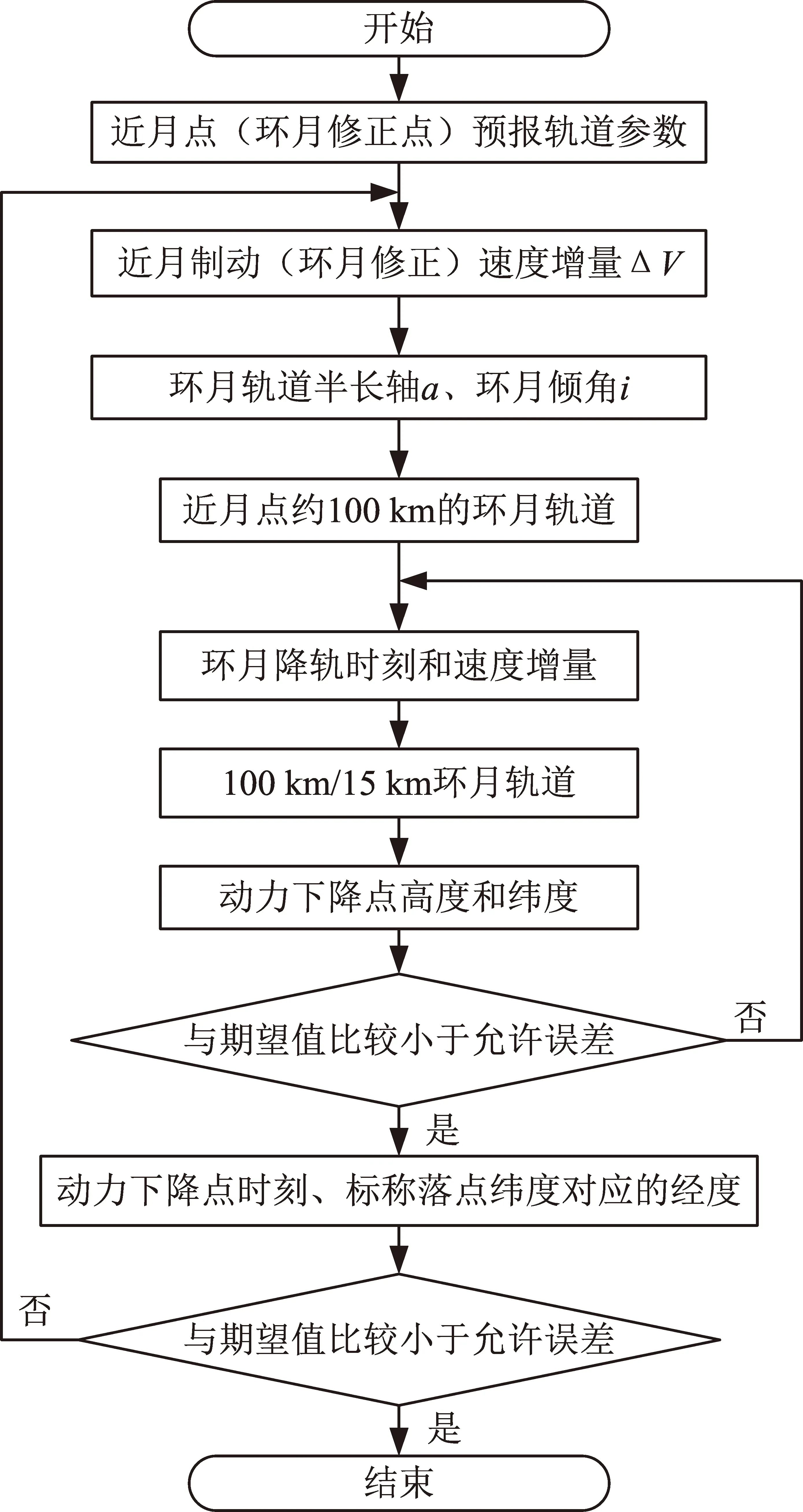
图3 嫦娥四号着陆器双层迭代轨道控制策略

双层迭代的轨道控制策略计算流程如下：

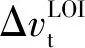
对于近月制动

(8)

(2)得到近月变轨量后，叠加到近月点制动前的轨道状态，预报至环月降轨点，进入第二个内层迭代，目标变量为动力下降初始点(同时也是此时环月轨道的近月点)高度和纬度，设计变量为环月降轨点纬度幅角和切向轨道控制速度分量，当动力下降初始点高度和纬度值与目标值误差满足允许误差，结束计算。

(9)

(3)得到环月降轨变轨量后，叠加到环月降轨前的轨道状态，将轨道预报至动力下降初始点，得到动力下降初始点纬度φd、轨道倾角im、动力下降航程L和动力下降飞行时间Td，计算月面着陆点经纬度(λL、φL)和着陆时刻TL。

由动力下降航程L，动力下降纬度φd和倾角im计算落点纬度φL过程如图4所示。

图4 动力下降段几何示意图

(10)

对应升轨

(11)

对应降轨

(12)

式中：Rm为月球参考半径，一般取1 737.4 km。

则落点纬度φL为

(13)

由落点纬度φL和倾角i计算落点经度λL为

对应升轨

(14)

对应降轨

(15)

式中：ωm为月球自转角速度，一般取2.661 7×10-6rad/s。

(4)计算得到月面着陆点经纬度(λL、φL)和着陆时刻TL后，进入外层迭代，目标变量为着陆点时刻、着陆点经度，设计变量为环月半长轴am和轨道倾角im。

(16)

当月面着陆点经纬度和着陆时刻与目标值误差满足允许误差，结束计算，进入计算步骤(1)。

(5)在近月制动完成后，以近月制动轨道控制后定轨参数替代近月制动前定轨参数，按步骤(1)～(4)计算环月修正轨道控制速度增量大小和方向。

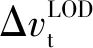
(17)

当目标变量与目标值误差满足允许误差，结束计算。

使用以上策略设计标称轨道，得到的标称轨道参数如表2所示。

由表2可知，嫦娥四号探测器每一个发射窗口的标称环月轨道半长轴和倾角不相同，但对应的标称落点和动力下降点时刻均相同，实现了理论上的定时定点着陆。

3 轨道控制策略实施

使用双层迭代轨道控制策略设计标称轨道，使得不同的发射窗口均可实现的定时定点着陆，但在实际飞控由于定轨、轨道预报和轨道控制执行等均存在误差[10]，需要在近月制动、环月修正和环月降轨时加入法向修正，相应的变轨策略则变由“2对2”变成“3对3”，这样通过双层迭代策略的多次应用，使得动力下降初始点预报的落点经度误差满足任务要求。

在飞控实施的过程中，环月段月球引力场采用100×100的高精度模型，由于环月时间较长，考虑兼顾计算效率和执行精度，将地月转移段和环月段解耦，地月转移段的中途修正瞄准标称的近月点高度和环月轨道倾角，从使近月制动开始，每次变轨同时使用面内面外变轨以确保定时定点的着陆任务要求，飞控过程中从近月制动到环月降轨历次轨道机动执行的轨道控制量的法向修正量如表3所示。

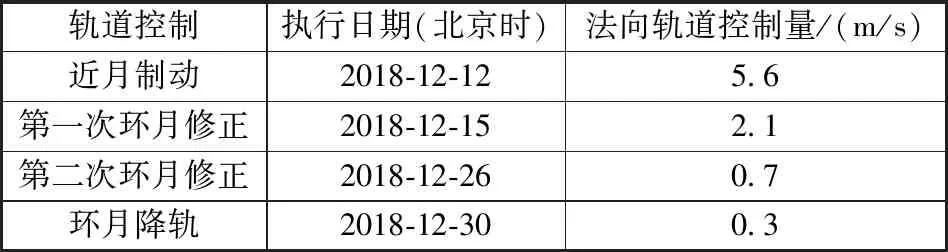
表3 飞控实施轨道控制策略的法向修正量

从飞控中法向轨道控制量的实施结果来看，控制量越来越小，这表明通过多次应用双层迭代的轨道控制策略，逐次减小了轨道控制残差，最终根据动力下降初始点定轨参数预报的落点经度差仅为0.004°，落点时刻预报误差小于25 s，完全满足任务要求。

4 结束语

在嫦娥三号轨道控制策略的基础上，针对嫦娥四号任务目标，在考虑测控条件、环月倾角接近90°的条件约束下，在标称轨道设计时，利用双层迭代的高精度“定时定点”月面软着陆轨道控制策略，使得不同的发射窗口实现理论上的月面定时定点着陆；然后在飞控实施阶段，在近月制动、环月修正和环月降轨等轨道控制同时进行切向和法向轨道控制，多次应用该策略，可减小轨道控制残差，获得的动力下降初始点定轨参数对应理论月面落点经度误差仅为0.004°，落点时刻预报误差小于25 s，为实现月面定时定点着陆提供了良好的初始条件。若在该轨道控制策略的基础上，动力下降段制导律具备一定的针对确定落点的调整能力，则可实现完全的月面定时定点着陆，这在我国将来的建立永久月球基地等月球后续探测任务中具有重要应用价值。