知识追踪模型融入遗忘和数据量因素对预测精度的影响

叶艳伟 李菲茗 刘倩倩 林丽娟

【摘要】 近年来，在线学习的人越来越多，在在线教学过程中教育者需要同时面对更多学习者，不可能了解每一个学习者的知识弱点与问题领域，并据此为学习者提供个性化的学习指导。本研究的目的是及时、准确推断学习者的问题领域，让学习者清楚自身的知识弱点，让教育者更加了解每一个学习者的知识水平，让在线学习系统自动向学习者推荐高效的学习路径和恰当的学习资源。在实验中，分析对比了知识追踪模型及其扩展模型的预测精度，分析了扩展模型使用学习者的所有数据与每个学习者的部分数据的预测准确性差异。结果显示：知识追踪模型可以较好估计学习者知识掌握情况;知识追踪扩展模型的预测精度更好;模型使用学习者部分数据可以获得比使用全部数据更好的预测精度;在学习者学习过程中遗忘时时存在，扩展模型使用部分数据在加快运行进度的同时更有利于精确估计学习者知识水平进而推荐更有效的个性化学习资源与学习路径。

【关键词】  在线学习;知识弱点;问题领域;学习路径;学习资源;知识追踪及其扩展模型;预测精度;預测准确性差异

【中图分类号】  G40-057       【文献标识码】  A       【文章编号】  1009-458x（2019）8-0020-07

一、研究背景

自20世纪60年代初以来，计算机系统一直被用于教育目的。近年来，随着Web计算技术的快速发展在线学习系统在教育中越来越普及，吸引了数百万学习者注册学习多元化的在线课程（Esichaikul， et al. 2011）。从教育研究的角度来看，在线学习系统有几个重要的优势，最显著的是记录学习者详细的学习轨迹，提供了分析不同轨迹下学习者行为效果的条件。然而，与面对面课程相比，传统的在线学习系统中知识是通过各种冗余信息自我寻求，且每个学习者的学习类型不同、具有不同的学习需求，因此在线学习系统对于学习者选择什么样的学习资源和学习路径缺乏个性化的教学指导（Chrysafiadi & Virvou， 2013）。

正因为如此，当前需要研究智能辅导系统。智能辅导系统是一种特殊类型的在线学习系统，其主要目的是在与学习者的交互中模仿人类教师行为来更好地了解学习者，以便自动确定在每种情况下教什么和如何教（Ha， et al. 2018）。目前主要通过学习者建模来实现这一目的。学习者建模是智能辅导系统的主要任务之一（Sison & Shimura， 1998）。知识追踪模型是一种用于建模学习者知识掌握情况的主流方法，旨在通过观察学习者的表现（如学习者在练习中回答问题的正确性）或学习者的行为（如学习者回答每个问题的时间）来估计学习者的潜在隐藏属性（如知识、目标、偏好和激励状态等无法直接确定的属性），并推断每个学习者知道什么，不知道什么（闾汉原， 等， 2011）。本研究的目的是采用知识追踪及其扩展模型更好地预测学习者的知识掌握水平、决定智能辅导系统这位“智能教师”需要为每个学习者提供的个性化学习资源和个性化学习路径，为未来高效地采用知识追踪模型进行研究提供一定的借鉴和参考。

本文介绍了知识追踪及其扩展模型，作为一个案例探究，评估了知识追踪及其扩展模型预测学习者未来表现的正确率，并将模型使用所有学习者的数据与每个学习者的部分数据的预测准确性进行了比较。

二、知识追踪模型

知识追踪模型由阿特金森（Atkinson）于1972年首次提出（Pardos & Heffernan， 2010），是模拟学习者知识掌握情况的一个很典型的模型，由Corbett和Anderson（1994）引入智能教育领域，目前已经发展成为智能辅导系统中对学习者知识掌握情况建模的主流方法，它使用动态贝叶斯网络利用学习者对给定知识问题的正确和不正确回答序列来推断学习者知识掌握情况，重新计算学习者对给定知识的掌握水平。知识追踪模型的目标是根据观察到的学习者在给定知识上的问题表现（t-1）推断学习者在问题t对于特定知识的掌握概率。学习者对知识作答的表现是二元的：要么正确，要么错误。科贝特（Corbett）和安德森（Anderson）提出的知识追踪模型假设遗忘概率[P（F）]为0，也就是说，学习者在知识学习的过程中不存在遗忘现象，因此知识追踪模型赋予每个知识点四个参数来表示每个学习者的知识水平（Hawkins， et al. 2014），分别为两个学习参数、两个表现参数：[P（L0）]和[P（T）]是学习参数，[P（L0）]指的是学习者尚未开始学习时知道特定知识的初始概率;[P（T）]指的是学习效率，即经过一段时间学习之后对于知识点从不会到会的转换概率，主要用来表示学习者的学习情况。[P（G）]和[P（S）]是学习者的表现参数，[P（G）]是猜对的概率，即学习者即使不知道知识点仍然回答正确的概率;[P（S）]是失误的概率，即学习者知道知识点，但是仍然回答错误的概率（王卓， 等， 2015）。具体知识追踪模型如图1所示（Gong， et al. 2010）：

知识追踪模型实际上是一个特殊的具有两状态的隐马尔可夫模型（Martori， et al. 2015），两状态表示学习者对于特定知识掌握或未掌握。模型中的每一个节点都通过条件概率表（Conditional Probability Table，CPT）来量化父节点对自身的影响，知识节点与表现节点的CPT如表1所示，表现节点在知识追踪模型中是已知态，或为正确，或为错误。每次学习者给出答案后，知识追踪模型基于该学习者答题正误的序列，使用贝叶斯公式迭代地更新学习者对知识的掌握程度以及预测该学习者再次遇到该知识点时的未来表现。

根据对以上知识追踪模型的分析，很容易得到答对答错时的概率公式和知识水平更新算法（Yudelson， 2016），这些公式被用来预测学习者做题表现的概率，算法用来更新学习者知识掌握水平。

（1）根据做题数据训练好参数之后，预测学习者做题表现的概率。

当答对题目时，学习者答对题目的概率被解释为在知道知识点的情况下没有犯错，以及在不知道知识点的情况下猜对的概率之和，即

[P（CorrectLk）=P（Lk）P（?S）+P（?Lk）P（G）]

当答错题目时，学习者答错题目的概率被解释为在知道知识点的情况下犯错，以及在不知道知识点的情况下猜错的概率之和，即

[P（IncorrectLk）=P（Lk）P（S）+P（?Lk）P（?G）]

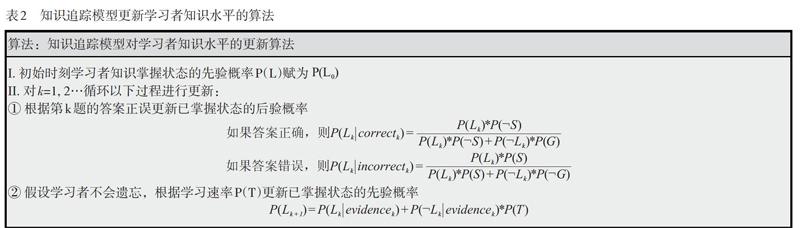
（2）知识追踪模型分为两个阶段：一是上面提到的利用学习者的大量答题序列训练模型参数;二是利用已训练好的模型基于学习者每次答题正误的序列迭代更新其对知识掌握的程度值，知识掌握情况迭代更新的算法思想如表2所示，其中[P（L）]表示所有学习者对知识点掌握的初始情况，[P（Lk）]表示学习者在回答第k道题之前对相应知识已掌握的先验概率，而[PLk|evidencek]表示根据学习者第k道题回答情况更新已掌握知识的后验概率。另外，最后一个等式表示的就是学习者答题后收到系统反馈时的学习转化过程，这个公式在加入学习概率后计算新的先验概率。

知识追踪模型的四个参数代表学习者知识水平[P（L0）]、学习者的学习智力[P（T）]、学习者的学习猜测[P（G）]和学习者的学习失误[P（S）]。对参数的不正确估计会错误评估学习者知识状态，导致教育者给出额外的任务以及在线学习系统提供低效率的学习资源与学习路径。此外，对参数的不正确估计，研究人员解释模型会得出不准确的科学结论。因此，获得正确的参数是至关重要的，将使研究人员真正了解学习者的知识状态。

三、研究目的和研究方法

（一）预测学习者未来表现

在实验第一阶段中采用Murphy使用Matlab中的Bayes Net Toolbox开发的程序来实现知识追踪模型和期望最大化（EM）算法分析学习者特定知识掌握水平，预测学习者未来表现，并限制[P（G）]和[P（S）]的值，因为[P（G）]大于0.5意味着没有掌握知识的学习者更可能做出正確回答，[P（S）]大于0.5意味着掌握知识的学习者更可能做出错误的回答，显然这种情况违反了知识水平和学习者表现之间的关系，即知识追踪模型出现模型退化现象（Pardos & Heffernan， 2010）。

（二）提高学习者未来表现预测精度

Corbett和Anderson（1994）提出的知识追踪模型假定学习者在知识学习过程中不存在遗忘现象，但本研究认为学习中遗忘是无处不在的，如果以前学习的知识一段时间内没有使用，则忘记它的可能性会更高（Nedungadi & Remya， 2015）。为了验证遗忘参数对知识追踪模型的预测能力是否产生影响，在实验第二阶段中使用知识追踪扩展模型（即在最初提出的知识追踪模型四个参数的基础上增加一个遗忘参数并设置不为0，代码实现上不是把遗忘参数当0即不存在对待，而是在赋予学习者初始遗忘的基础上通过学习数据迭代出学习者遗忘概率值）分析学习者特定知识掌握水平，预测学习者未来表现，并对比实验第一阶段中模型预测表现精度，判断知识追踪扩展模型相对于知识追踪模型是否提高了学习者未来表现的预测精度，即学习者学习过程中的遗忘因素是否可以忽略。

（三）学习者部分数据对知识追踪扩展模型未来表现预测精度影响分析

为了验证知识追踪扩展模型采用学习者部分数据对未来预测表现精度的影响，在实验第三阶段中使用知识追踪扩展模型，根据采用每个学习者数据量的多少分组进行对比分析研究（Nooraei， et al. 2011）。另外，如果实验第二阶段在预测学习者未来表现时证实遗忘不可忽略，那么学习者作答时间越靠前的问题对于模型获得相对完美参数的干预就越强，因此对比分析了知识追踪扩展模型使用每个学习者学习数据的后1/3、后1/2、后2/3量的数据与使用完整数据分析学习者知识水平预测未来表现的精度，或者说这是一种使用知识追踪扩展模型探索选择数据集后部分数据度与完整数据集在降低模型运行时间的同时提升模型预测精度的方法。

四、实验设计

（一）实验数据集

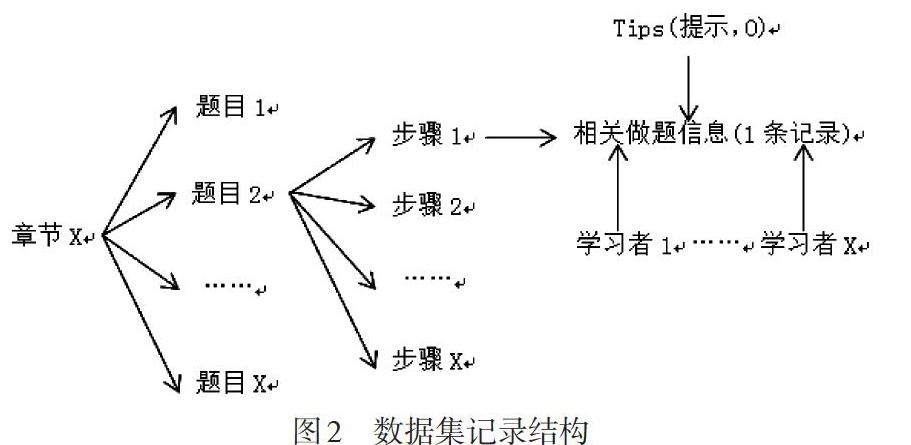
实验数据集来自名为Bridge to Algebra的在线教育系统，该数据集也是2010年KDD（knowledge discover and data mining）Cup比赛数据，由卡内基学习公司提供，可从http：//pslcdatashop.web.cmu.edu/KDDCup下载。卡内基学习公司是一个面向中学和大学学习者学习的智能辅导系统的制作公司，该数据集是关于学习者数学课堂教学学习过程数据，包含6，043名学习者的20，012，498项记录，每项纪录包含学习者ID、知识点所属章节、问题类型、步骤类型、开始及结束时间、回答正确或错误、请求提示次数、知识点类型、做题次数等19条信息，数据集记录的结构（如图2所示）可以表述为每一章节中学习者做的每一道题被分成了许多步骤，系统记录每一个步骤的做题情况，并且在做题过程中学习者可以请求系统中的提示，但是请求提示后该题无论正确与否都标记为错误。KDD Cup 2010是免费提供的最大的学习者学习的数据集合，本研究从KDD Cup 2010数据集中选择了数据集的一个子集，即学习者在概率单元第四小部分的学习过程样本，此样本包括200个学习者，每个学习者包括30个维度问题答案，共6，000个样本数据点作为知识追踪模型的训练和测试数据集。

（二）研究流程

实验分为三个阶段：第一阶段主要是验证知识追踪模型可以得到比较理想的预测未来表现的精度，能较真实地反映学习者的知识水平，为学习者提供相对恰当的学习资源和学习路径;第二阶段主要是采用知识追踪扩展模型（遗忘参数不为0）来对比知识追踪模型的未来表现预测精度，在验证学习者学习过程遗忘参数存在的基础上更准确地反映学习者真实知识水平，提供与学习者真实知识水平更适合的学习资源和学习路径;第三阶段主要是给予知识追踪扩展模型不同的学习者后数据度进行训练，对比模型使用学习者的后部分数据与使用全部数据的预测精度，验证模型使用学习者后部分数据在加快运行速度的同时提高预测精度，且能为学习者提供更恰当和高效的学习资源与学习路径并与学习者真实知识水平贴合度更高、误差更小的猜想。具体实验流程如图3所示：

[参考文献]

闾汉原，申麟，漆美. 2011. 基于“态度”的知识追踪模型及集成技术[J]. 江苏师范大学学报（自然科学版），29（4）：54-57.

王卓，张铭. 2015. 基于贝叶斯知识跟踪模型的慕课学生评价[J]. 中国科技论文，10（2）：241-246.

Chrysafiadi， K.， & Virvou， M. （2013）. Student modeling approaches： A literature review for the last decade. Expert Systems with Applications， 40（11）， 4715-4729.

Corbett， A. T.， & Anderson， J. R. （1994）. Knowledge tracing： modeling the acquisition of procedural knowledge. User Modeling and User- Adapted Interaction， 4（4）， 253-278.

Esichaikul， V.， Lamnoi， S.， & Bechter， C. （2011）. Student modeling in adaptive e-learning systems. Knowledge Management & E-Learning： An International Journal， 3（3）， 342-355.

Gong， Y.， Beck， J. E.， & Heffernan， N. T. （2010， June）. Comparing knowledge tracing and performance factor analysis by using multiple model fitting procedures. In International conference on intelligent tutoring systems （pp. 35-44）. Springer， Berlin， Heidelberg.

Ha， H.， Hong， Y.， Hwang， U.， & Yoon， S. （2018）. Intelligent Knowledge Tracing： More Like a Real Learning Process of a Student. arXiv preprint arXiv：1805.10768.

Hawkins， W. J.， Heffernan， N. T.， & Baker， R. S. （2014， June）. Learning Bayesian knowledge tracing parameters with a knowledge heuristic and empirical probabilities. In International Conference on Intelligent Tutoring Systems （pp. 150-155）. Springer， Cham.

Martori， F.， Cuadros， J.， & González-Sabaté， L. （2015）. Direct Estimation of the Minimum RSS Value for Training Bayesian Knowledge Tracing Parameters. International Educational Data Mining Society.

Nedungadi， P.， & Remya， M. S. （2015， March）. Incorporating forgetting in the personalized， clustered， bayesian knowledge tracing （pc-bkt） model. In 2015 International Conference on cognitive computing and information processing （CCIP） （pp. 1-5）. IEEE.

Nooraei， B. B.， Pardos， Z. A.， Heffernan， N. T.， & de Baker， R. S. J. （2011）. Less is More： Improving the Speed and Prediction Power of Knowledge Tracing by Using Less Data. In EDM （pp. 101-110）.

Pardos， Z.， & Heffernan， N. （2010， June）. Navigating the parameter space of Bayesian Knowledge Tracing models： Visualizations of the convergence of the Expectation Maximization algorithm. In Educational Data Mining 2010.

Pardos， Z. A.， & Heffernan， N. T. （2010， June）. Modeling individualization in a bayesian networks implementation of knowledge tracing. In International Conference on User Modeling， Adaptation， and Personalization （pp. 255-266）. Springer， Berlin， Heidelberg.

Sison， R.， & Shimura， M. （1998）. Student modeling and machine learning. International Journal of Artificial Intelligence in Education （IJAIED）， 9， 128-158.

Yudelson， M. （2016）. Individualizing Bayesian Knowledge Tracing. Are Skill Parameters More Important Than Student Parameters.In EDM （pp. 556–561）.

收稿日期：2018-07-02

定稿日期：2019-02-27

作者简介：叶艳伟，硕士研究生;刘倩倩，硕士研究生;林丽娟，硕士研究生。浙江工业大学教育科学与技术学院（310023）。

李菲茗，博士，教授，碩士生导师，本文通讯作者，浙江师范大学教师教育学院（321004）。

责任编辑 张志祯 刘 莉