积累N次主动变换的传导知识挖掘

王丰，顾佼佼，林瑜

（海军航空大学，山东 烟台 264001）

相关性是可拓学[1-2]中进行主动变换及引起传导变换的基础。复杂的相关关系网中，只有在两个信息元之间存在相关性的前提下，当对其中一个信息元特征的量值实施主动变换时，才会引起另一个信息元发生传导变换。然而，现实情况中，当对一个信息元实施一次主动变换时，并不能引起与之相关的信息元发生传导变换。而只有积累实施N次主动变换后，才能引起与之相关的信息元发生传导变换。N非固定取值，也会随着时间或场景的变化而不同。例如，某酒店在把饭菜价格提高后，其就餐人数并未发生变化，营业额和利润增加了。某段时间后，该酒店再次将饭菜价格进行了提高。本次提价后，酒店的就餐人数、营业额和利润都减少了。目前，关于类似累计的主动变换及传导效应的研究文献还未见。

对信息元某特征的量值而言，如何从累积多次的主动变换中挖掘出有用的传导知识，将会对分析所实施的主动变换有着至关重要的作用。为此，本文在主动变换、相关性、传导变换、传导效应的基础上，结合灵敏度的概念，重点研究某特征的量值累积多次主动变换后, 引起的传导变换的传导知识挖掘理论，丰富了可拓学的传导知识数据挖掘[3-4]理论。为传导知识的数据挖掘提供了一个新方法和新思路，使传导知识数据挖掘理论更加全面。

1 积累多次主动变换的传导特征

为了方便，仅研究两个相关信息元之间的主动变换[5-8]及其传导变换。记信息元

2 积累多次主动变换的传导效应

信息元

3 主动变换关于目标特征的灵敏度

归一化得

4 实例分析

假设某型导弹武器Q的导航系统[14-17]中，部件A和部件B存在相关关系。部件A某个模块的振动值记为，部件B的平衡性能记为，导弹武器系统Q的整体性能记为。在该导弹武器系统[18]研究定型过程中，累计了大量的试验数据。限于篇幅，通过10次试验数据，结合本文方法挖掘部件A的振动值对导弹武器系统Q的整体性能的传导知识。假设10次试验数据的量值如表1所示。

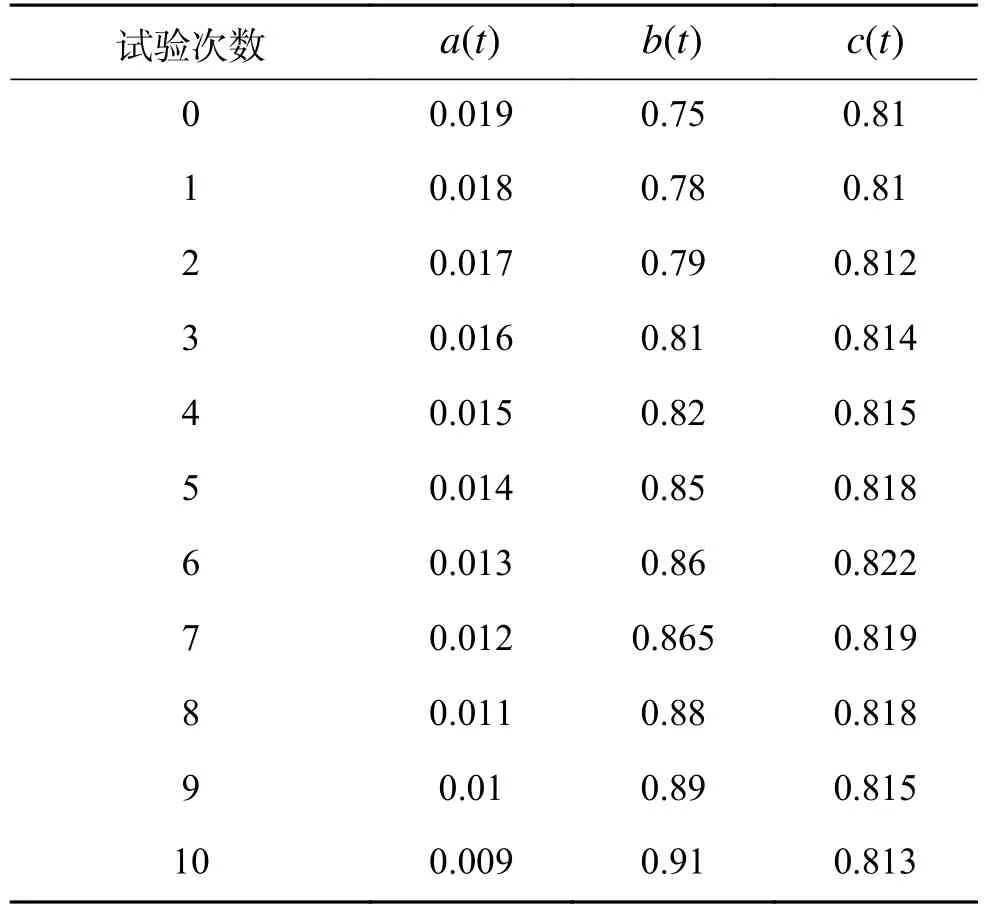
表1 10次试验数据的量值Table 1 Values of 10 test data

将导弹武器系统Q的整体性能、部件A和部件B分别用信息元刻画为

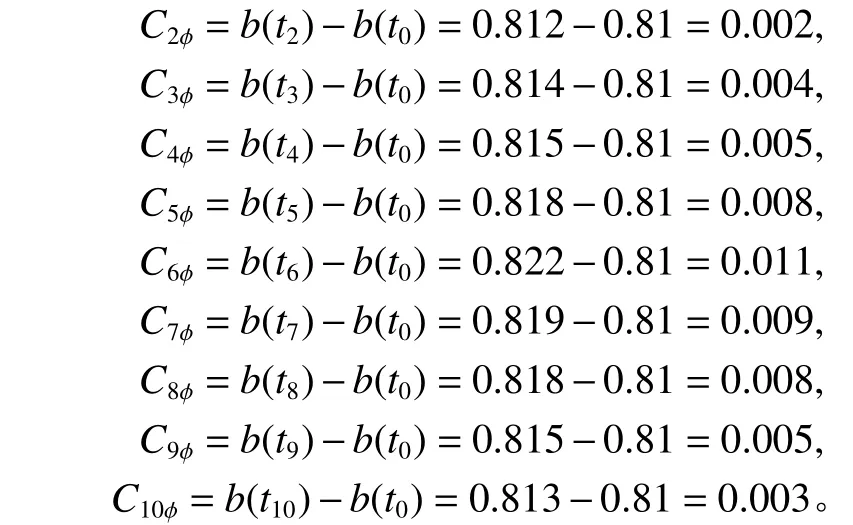
从表1中可见，在第6次试验(对部件A实施第6次主动变换)中，目标特征的量值最大。前6次主动变换关于特征的平均变换量

5 结束语

现实问题中，经常遇到前N次可拓变换未引起与之相关的信息元发生传导变换，而N+1次主动变换才能引起与之相关的信息元发生传导变换的情况。本文为了挖掘N+1次积累主动变换的传导知识理论，将可拓变换、传导效应和灵敏度的概念引入到传导知识的挖掘中,充实和完善了传导知识的挖掘理论。下一步，将结合该型导弹武器系统工厂试验及设计、定型试验过程中产生的大量试验数据，利用计算机编程仿真，深入挖掘各项特征对该型战术导弹武器系统性能特征的灵敏度，为其定型、列装和改进提供理论和实践参考依据。