一种TOA联合同步与定位的CWLS算法

田 强，冯大政，胡豪爽

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

无线目标定位技术广泛应用于雷达、麦克风阵列和传感器网络等领域[1-3]，一直以来都是信号处理方向的研究热点。常见的定位技术分为：基于到达时间(Time Of Arrival, TOA)定位，基于到达时间差(Time Difference Of Arrival, TDOA)定位，基于到达角定位以及基于接收信号强度定位等[4-6]。其中，基于到达时间的定位技术所需的测量设备相对简单，具有定位方程非线性程度低，定位精度高等优点，因而受到越来越多的关注。

到达时间定位的原理是利用传感器获取目标信号到达时的传输时延，并计算出二者之间的距离，然后以此构建定位方程，确定目标的位置。传感器获取信号传输时延需已知目标信号的发射时间，因此，传统的达到时间定位技术一般要求目标与传感器之间是精确同步的。而在实际应用中，二者往往存在时钟偏差，尤其在对非合作目标定位时，更加难以满足与传感器网络时钟同步的要求。考虑到目标信号在空气中近似以光速传播，因此，即便是非常微小的时钟偏差，也会导致较大的距离估计误差，进而严重影响目标定位精度。目前针对以上不同步问题的解决方法主要分为两种：一是将传感器接收的数据相减，消除时钟偏差，转化为时差定位进行求解；二是将时钟偏差也当作未知变量与目标位置一起进行联合估计。文献[7]研究表明，这两种方法理论上都不存在信息损失，具有相同的克拉美罗界(Cramér-Rao Lower Bound，CRLB)。但第一种处理方法进行量测数据相减，不仅会引入有色噪声，而且导致非线性程度变高，增加了实际解算的难度，更容易引起较大的定位误差。相对而言，联合估计处理方法在实际解算中可以获得更高的定位精度。

联合时钟同步与目标定位本质上是一个非线性求解问题，解算方法主要分为迭代类算法、闭式解算法和凸优化方法。常用的迭代类方法包括泰勒级数法(Taylor Series, TS)[8]，牛顿法[9]等。这类方法需要一个接近真实值的迭代初始值来保证全局收敛性；在初始值选取不好的情况下，容易落入局部极小点，难以得到令人满意的解。闭式解算法无需进行迭代运算，具有计算量小的优点。文献[10]利用加权最小二乘(Weighted Least Square, WLS)准则，将原问题转化为对二次方程的求解，得到目标位置和时钟偏差的闭式解。然而，实验表明其定位精度并不能达到克拉美罗界。文献[11]提出了两步加权最小二乘(Two-Step WLS, TSWLS)算法，首先引入辅助变量将原非线性观测方程转化为伪线性方程，并利用加权最小二乘准则获取初值，然后利用变量之间的关系对初值进行校正，最终得到目标参数估计的解析解。该方法在测量误差较小时，定位精度逼近克拉美罗界；但是当测量误差较大时，定位性能将严重下降。凸优化方法是通过利用凸松弛技术，将原非凸的定位问题转化为半正定规划[12]或者二阶锥规划[13]等凸优化问题进行求解。这类方法的优势是迭代优化过程不依赖于初始值的选取，且能够保证全局收敛性[14]。然而，由于对原问题进行了松弛近似，该方法在大部分情况下只能得到次优解。因此，笔者提出了一种新的联合估计算法，该算法利用变量之间的相互关系构造约束条件，将原问题转化为约束加权最小二乘问题进行求解。理论分析了该算法的有效性，实验表明该算法性能优于现有的联合估计算法。

1 定位模型

假设在二维平面内分布了M个时钟相互同步的传感器锚节点，其坐标已知且分别表示为si=[xi,yi]Τ,i=1,2,…M；待估计的目标节点坐标为x=[x,y]Τ。目标x与传感器si之间的距离可表示为

di=‖x-si‖2,i=1,2,…,M。

(1)

假设目标与各传感器节点之间存在的时钟偏差为τ，不考虑非视距传播的影响，则第i个传感器节点接收到目标信号时的本地时间为

(2)

式中，c为信号传播速度，一般近似为光速；Δti表示时间测量误差。将式(2)乘c转化为距离量，有

ri=cti=di+r0+ni,i=1,2,…,M,

(3)

令r=[r1,r2,…,rM]Τ，d=[d1,d2…,dM]Τ，则式(3)可以写成如下的矢量形式：

r=d+r0+n，

(4)

式中，n=[n1,n2,…,nM]Τ，为测量误差矢量，其协方差矩阵表示为Qn=E[nnΤ]。由此易得关于目标位置x和时钟偏差r0的最大似然估计等价于如下最小化问题：

(5)

求解问题(5)可以得到x和r0的估计值。然而，式(5)中的代价函数是非线性、非凸的，难以直接求解。

2 算法描述

2.1 构造约束加权最小二乘估计

在式(5)中，将r0移到方程的左边，然后两边同时取平方，经过整理可得

(6)

Aφ-b=ξ，

(7)

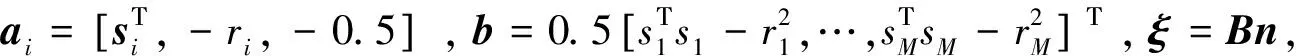
可以看到，式(7)是关于φ的线性方程，根据加权最小二乘理论，可得到关于φ的代价函数为

(8)

qΤφ+φΤpφ=0 ，

(9)

在问题(8)中加入约束条件(9)，原联合估计问题可以转化为如下约束加权最小二乘估计问题：

(10)

2.2 利用拉格朗日乘子法求解

式(10)是一个具有二次等式约束的二次优化问题，根据拉格朗日乘子法，式(10)等价于如下最小化问题：

(11)

式中，λ为拉格朗日乘子。用式(11)的目标函数对φ微分，并让结果等于0，经整理可得φ的估计值为

(12)

然而，在上式中需要进一步求解未知参数λ。将式(12)代入到式(10)的约束条件中，可得

(13)

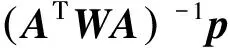
(14)

(15)

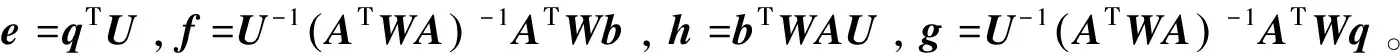
(16)

(17)

式中，aj=0.25γjejgj-0.5ejgjγj，bi=ejfjγj-0.5ejgj-0.5γjhjgj-0.5γjejfj，cj=ejfj+γjhjfj。

式(17)是一个高次多项式方程，利用Matlab中的卷积运算(conv)和多项式求根运算(root)可以很容易求得λ的解，然后进一步得到φ的估计值。具体步骤如下：

步骤1 利用Matlab中的conv和root函数求解式(17)，得到拉格朗日乘子λ的多个解。

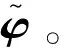
2.3 性能分析

克拉美罗界确定了所有无偏估计误差协方差理论上所能达到的下界，以此为标准可以有效分析文中算法的定位性能。设θ=[xΤ,r0]Τ，由文献[10]和[11]可知，基于到达时间的联合同步与定位问题的克拉美罗界为

(18)

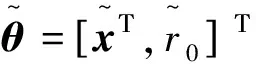
将A按列分解为A=[A12,A3,A4]，其中A12、A3和A4分别表示A的1～2列、第3列和第4列。则代价函数式(10)可以重新写为

f(θ)=gΤWg，

(19)

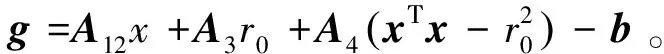
(20)

其中，J=[A12+2A4xΤ,A3-2A4r0]是f(θ)的雅克比矩阵。下面对g进行一阶小误差扰动分析。

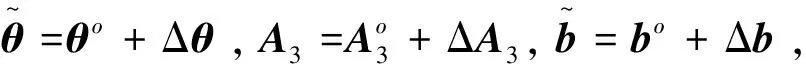
g=Bn+JΔθ。

(21)

(22)

(23)

3 仿真实验

下面将文中算法的估计性能与文献[8]中的泰勒级数法(TS)、文献[10]中的加权最小二乘算法(WLS)、文献[11]中的两步加权最小二乘算法(TSWLS)、文献[12]中的最小-最大算法(MMA)[12]以及式(23)的克拉美罗界(CRLB-TOA)进行对比来评估算法的性能。文中算法还对比了时差定位的CRLB[15](CRLB-TDOA)和时差定位中经典的Chan算法[15](Chan-TDOA)。为了方便比较，采用估计偏差和均方根误差来衡量算法的性能，其定义分别为

(24)

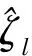
图1描绘了在不同的测量误差下各算法的估计偏差。从图中可以看出，当测量误差较小时，文中算法和其他算法的估计偏差都趋于0，近似为无偏估计；这与2.3节中理论分析结果是一致的。随着测量误差的增大，各算法的估计偏差都有所增大，而文中算法的估计偏差增加的相对缓慢且一直保持最小。

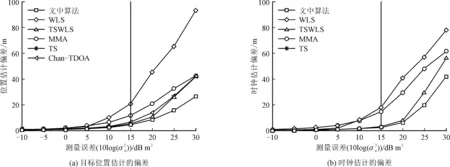
图1 各算法的估计偏差随测量误差变化的统计结果

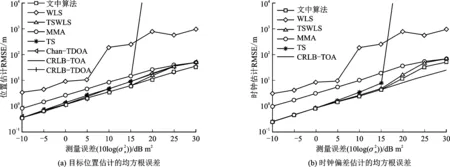
图2 各算法的估计均方根误差随测量误差变化的统计结果

图3 定位误差累积分布函数

值得注意的是，文中算法与TSWLS算法一样都是通过引入辅助变量对原问题进行伪线性化的，而文中算法的性能优于TSWLS算法。其中的主要原因是，TSWLS算法在第一步中忽略了变量之间的耦合关系而直接对伪线性方程进行加权最小二乘求解，人为地引入了额外的误差；而且在第二步中进行误差校正时，所使用加权矩阵又是通过一阶扰动分析近似求解的，当测量误差较大时，定位精度明显降低。文中算法将变量之间的关系当成约束条件与代价函数一起求解，避免了分步运算，最大限度地减少了人为误差的引入，从而提升了目标定位的精度。

4 结束语

目标与传感器之间的时钟偏差的存在会严重影响传统到达时间定位的性能，笔者针对这一问题提出了一种联合同步与定位算法。利用变量之间的耦合关系构造约束条件，将原问题转化为约束加权最小二乘问题，然后利用拉格朗日乘子法进行优化求解。理论上分析了该算法的有效性。实验结果表明，相比较传统的迭代类算法、闭式解算法以及凸优化类算法，文中算法具有较高的估计精度。