订单共享下的多中心逆向物流路径优化
罗浩 李想 吉敏全


摘要:逆向物流的路径优化对降低回收成本具有重要意义,而回收成本直接影响着逆向物流行业的发展。本文针对逆向物流多中心的回收问题,基于共享订单协同回收的回收网络模式,在考虑逆向物流过程中的运输成本以及客户满意度的基础上以油耗和时间惩罚成本最小化为目标建立了车辆回收路径规划模型,并利用量子粒子群算法精度较高和收敛速度较快的优势对模型进行求解。最后通过算例分析证明了模型和算法的可行性和有效性,以期对多回收中心的逆向物流路径规划问题提供理论参考和实践指导。
关键词:订单共享;多回收中心;逆向物流路径优化;量子粒子群算法
中圈分类号:U116.2 文献标识码:A
0引言
随着经济的快速发展和现代城市化进程的加快,在物资消耗巨大的同时产生了大量有剩余价值的回收物品,使得社會对逆向物流服务的需求日渐增加。据统计,物流成本中有大约60%为运输成本,因此逆向物流过程中车辆路径的选择对降低逆向物流活动成本有着十分重要的影响。目前,国内外学者对逆向物流路径优化问题已有诸多研究。李勤以选址成本、收集成本和库存成本最低为目标函数建立了基于逆向物流的第三方物流仓储配送模型,对分区域回收的逆向物流回收模式下的车辆路径规划问题进行了研究;黄蕊唧等人针对逆向物流网络中废旧产品回收数量及再制品需求数量的不确定性,以整个物流网络中的总收益最大为目标,建立了多产品、多周期的再制造逆向物流网络优化模型;石丽红在考虑时间窗和容量约束的基础上对单物流回收中心的医疗废弃物回收网络车辆路径规划问题进行了研究;马祖军、代颖噬于混合整数线性规划方法建立了一种单产品、有能力限制的产品回收逆向物流网络优化设计模型,据此确定物流网络中各种设施的数量和位置,并在由此构成的各条物流路径上合理分配物流量,以使各种设施的投资和运营成本之和最小。孔祥莹针对时间敏感型回收品的特点,在考虑配送优先度和车辆运载空间充分利用的基础上对单回收中心的逆向物流配送路径规划问题进行了研究;宋志兰等人建立了使服务时间满足顾客时间窗约束的逆向物流冷链配送成本模型,对单回收中心的冷链逆向物流车辆路径问题进行了研究;乔佩利和王娜在考虑带退货和时间窗的基础上研究了闭环供应链下取送货一体化的车辆路径规划问题,建立了同时实现客户满意度最高和运营成本最低的路径优化模型。姬淑珍等人讨论了如何对订单合理分配实现货物的低成本及高效回收的问题,通过对逆向物流车辆与货物订单分配问题的分析,利用现代排序论的思想和方法将逆向物流订单和车辆分别看作工件和机器,构建了逆向物流订单分配排序优化模型,设计了模型求解算法。周根贵人构建了一个逆向物流网络中的选址模型,旨在研究从备选地址中选择建立配送中心或回收中心最佳策略,然后应用遗传算法讨论了该模型的具体解法。高更君认为在逆向物流供应链研究中,为了解决市场需求、供应商供货能力、回收产品数量等不确定问题以及逆向物流系统中存在的目标冲突,建立了制造商收益最大化和所选供应商不合格零件数最少化的多目标数学优化模型来确定最佳供应商选择、订单量分配以及提货点选址。Rahmatian Mohammad研究了多目标的逆向物流网络的设计与分析;王杰和卫航在多客户端的前提下研究了逆向物流的回收合作。上述研究为解决路径优化问题提供了较好的研究思路及独到见解,但在研究内容上以单回收中心的车辆路径优化和多回收中心单因素成本居多,在多回收中心逆向物流方面偏重于网络的设计研究,对于多订单多回收中心下逆向物流的路径优化研究较少涉及。本文是在多回收中心同时考虑两种成本因子,即车辆油耗和时间窗惩罚总成本最低的基础上建立了逆向物流车辆回收路径规划模型,并用收敛速度更快、寻优能力更好的量子粒子群算法进行求解,以期取得更好的逆向物流路径优化效果,为业界提供理论参考和实践指导。
1问题描述
逆向物流是指回收中心在接受各个客户的订单信息后派出车辆到各个回收点取货并运输到指定地点的过程。订单共享下的逆向物流回收模式是指先由多个回收中心分别接收客户订单,订单信息包括客户坐标、货物数量以及期望时间段等详细信息,然后将订单信息汇总后在各回收中心协同合作的情况下进行订单分配,由回收中心根据回收客户的需求量以及满足客户需求的服务时间对车辆和回收路线进行分配,从而规划出油耗成本最低以及超时惩罚成本最低的最优路径。订单共享前的分区域回收模式如图1左图所示,订单共享后的多中心逆向物流回收模式如图1右图所示,本文是站在全区域角度下考虑多中心回收的路径规划,将单回收中心局部优化问题转变为多回收中心全局优化问题进行处理。
2订单共事下多回收中心逆向物流的路径优化模型
2.1模型假设
(1)逆向物流回收中心和客户的位置均已知;(2)各回收中心的订单共享,每个客户的订单量已知,服务时间已知;(3)回收中心拥有不同型号的车辆,载重量和最大行驶距离已知,不考虑车辆拥堵问题且在运输过程中保持匀速行驶;(4)车辆每次从回收中心出发并最终返回到回收中心;(5)回收的货物为同质货物;(6)油耗与车辆载重和运输距离成正比关系。
2.2模型建立
根据问题描述,基于模型假设和参数设定,构建数学模型如下:
3算法设计及模型求解
3.1算法选择与设计
物流交通路径优化算法较多,传统算法以遗传算法(GA)、粒子群优化算法(PSO)运用居多。遗传算法(GA)反映了个体的适应度在整个群体的个体适应度总和中所占的比例,个体适应度越大,其被选择的概率就越高。但是遗传算法存在一定的不足之处:遗传算法通常的效率比其他传统优化方法低,且容易过早收敛。粒子群优化算法(PSO)是进化算法的一种,适合在动态多目标优化环境中求解,该算法精度高,收敛速度快,但是后期的收敛速度变慢,以至算法到一定程度后无法达到最优,有其局限性。
本文选择基于PSO算法并结合量子思想优势的量子粒子群(QPSo)算法,使每个量子粒子根据自身的历史经验以及其同伴的经验在N维空间寻求最优解,在寻求最优解的过程中,不断进行学习和调整,从而获取更优秀的解,具有较高精度和收敛速度。
3.2模型求解
4算例模拟
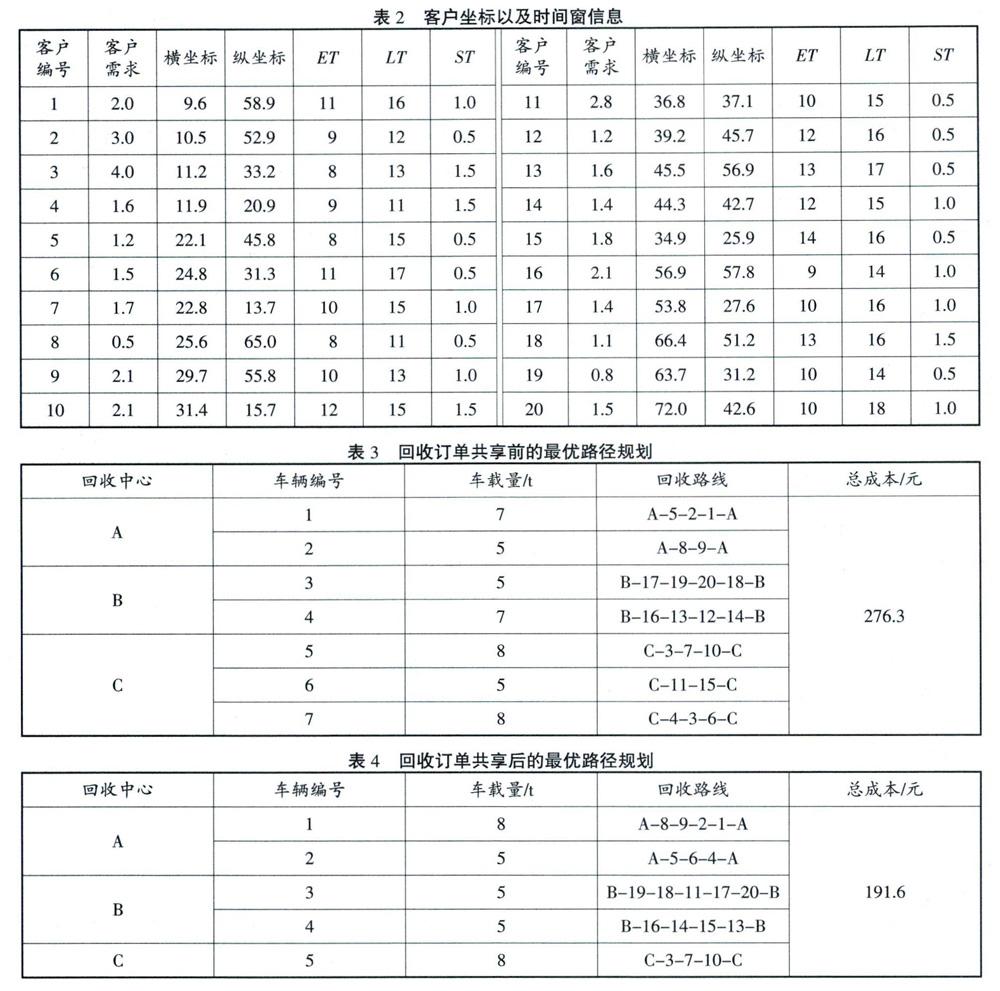
设在逆向物流回收网络中有3个回收中心,20个待回收客户点,订单共享前的回收中心服务范围见表1。车辆空载时的单位距离油耗0.068~0.071L/kin,满载时的单位距离油耗为0.078~0.081L/km,油耗成本为3.5元/L,车辆的最大行驶距离为130km,最大载重量为5t-8t,车辆匀速行驶速度为50km/h。回收过程中,提前到达客户时的单位时间成本为30,迟到惩罚的单位时间成本为50。回收网络中,3个回收中心的坐标分别为A(15,55)、B(55,40)、c(25,20),客户坐标(公里)、需求量(t)、时间窗信息(h)以及服务时间(h)如表2所示。
结果分析:首先用QPSO算法分别对订单共享前和订单共享后的最优路径进行规划,得到的结果见表3和表4,算法收敛图如图2所示。
通过对比可以发现实现订单共享后的逆向物流回收中心需要派出的车辆数目减少,油耗和时间惩罚成本也相应降低,证明了模型和算法的可行性和有效性。
为了验证QPS0算法的优越性,在matlabR2016中进行了仿真实验,分别运用经典的遗传算法、粒子群算法以及改进后的量子粒子群算法独立运行50次,将得到的结果求平均值进行对比,如图3所示,可以看出,量子粒子群算法的收敛速度和寻优能力整体更优。
5结论
本文针对多回收中心的逆向物流回收路径优化问题,在订单共享的条件下考虑了运输成本和客户满意度,即分别通过油耗成本和时间窗惩罚成本来体现对回收车辆的路径优化问题进行了研究,建立了以总成本最低为目标函数的路径规划模型,并利用量子粒子群算法的优势对模型进行求解,最后通过算例证明了模型和算法的可行性和有效性,以期对今后订单共享下的多中心逆向物流的回收路径规划提供理论参考和实践指导。鉴于本文是在比较理想的条件下进行的路径规划,对于不确定因素尚未做深入研究,不确定的逆向物流网络规划将作为后续研究的重点问题。

