考虑流量均衡的多配送中心选址优化方法
张敬涛 陈江行


摘要:在我国物流业飞速发展的背景下,文章主要研究考虑流量均衡的多配送中心选址问题,由此更好地处理物流选址中的实际需求。除去经典选址问题中对于距离因素的考量,纳入了对于配送中心之间物流流量均衡因素的考虑,并建立了相应的数学模型。设计了一种带约束的改进K-means聚类算法来求解该问题,最后采用当地企业的实际数据验证模型和算法的有效性,并对比分析了与经典聚类算法的不同之处。
关键词:配送中心选址;K-means算法;整数规划
中图分类号:F252.14
文献标识码:A
0引言
随着我国物流业务量的逐年增长,配送中心作为物流网络中的基础节点,扮演着越来越重要的角色。关于配送中心的选址问题,除了需要考虑距离的因素外,其他复杂因素例如当地交通情况,经济发展因素,服务范围等也需要纳入考量。本文研究了考虑物流流量均衡的多配送中心选址问题,即为了服务若干客户点,除了考虑与客户点之间的距离,还应保证各个配送中心所服务的客户的物流流量需求差异较小,使得每个配送中心的利用率相对均衡。图l为该问题的一个简单例子:三个配送中心分别覆盖的客户点的物流流量分别为250,230和280,若规定流量差异最大为50,则这种情况可视为各配送中心之间流量均衡。
目前国内外关于多配送中心选址的研究已经较为深入,其中聚类分析的思想是一种常见且重要的思想。其主要思路是将客户群通过聚类分成若干簇(客户群的子集),从而将多配送中心选址问题简化为若干个单配送中心选址问题。秦固、段华薇翻、饶良良以及Liu和Zhang人利用蚁群算法对客户点进行聚类然后分别求解单配送中心选址问题。ESNAF和KUCUKDENIZ、毛海军等、陈磊等则通过模糊聚类的方法,建立指标体系,将备选配送中心划分为若干类,然后在每一类中选择最优的配送中心。叶浔宇和孔继利等对客户点采用聚类分析进行分类后,利用重心法进行配送中心的选址。
除去上述方法,K-means作为一种经典的聚类方法,也在选址问题研究中得到了广泛应用。王信波等采用随机采样K-means方法进行GIS中心的选址。马大奎和陈铭通过K-means算法将全国二级城市进行聚类,并以此进行物流成本分析。Li等计二阶段的K-means算法,将配送中心的承载能力和辖射半径作为约束条件构建社区物流网络。刘威和王云婷等在K-means算法基础上分别利用模糊规则的证据推理法(ERA)和层次分析法对选址方案进行进一步的优化。
本文将提出一种改进的K-means算法,将K-means算法与整数规划方法集成,使得该算法可以高效处理选址问题中的约束,满足选址问题中的一些现实需求。
1问题建模
1.1问题描述
考虑流量均衡的多配送中心选址问题可以描述为:给定n个客户点,设每个客户点i的位置为(xi,yi),月订单量为qi。现需要建造m个相同规模的配送中心,要求决策这m个配送中心的位置,确定每个客户点所属的配送中心,使得客户点与所属配送中心的距离总和最短,并且任意两个配送中心的物流流量差值不超过给定阈值ε。
1.2模型建立
根据上述问题建立该选址问题的数学模型M。。模型中包含了以下基本假设:(1)任意一个坐标位置均能建设配送中心;
(2)客户点每月的物流流量需求恒定。
本问题的决策变量为每个配送中心的位置,即(aj,bj),以及0-1变量Oij,Oij=1表示客户点i由配送中心j服务,否则不由配送中心j服务。模型M构建如下:
上述模型说明如下:式(1)为目标函数,即客户点与所属配送中心的距离之和最小化。式(2)表示每个客户点只能由一个配送中心服务。式(3)表示任意两个配送中心之间的月物流流量差值不得超过阈值ε。
2集成流量均衡约束的K-means聚类算法
2.1算法设计
上述问题的数学模型M目标函数中含有非线性项,为非线性混合整数规划,因此无法直接使用规划求解器进行求解。本文以在选址问题中广泛应用的聚类算法为基础,在K-means算法的基础上集成整数规划方法,提出集成流量均衡约束的K-means聚类算法来获得该问题的较优解。区别于传统的K-means算法直接将客户点分配至最近的配送中心的策略,本算法通过整数规划求解得到满足给定约束的最优客户点分配方案。
本文算法的基本思路为:在K-means算法的框架下,通过上一次迭代得到的簇(每个配送中心所服务的客户集合)计算本次迭代的配送中心的坐标,由此模型M中的决策变量(ai,bi)转化为已知量,数学模型转化为仅有决策变量Oij的0-1整数规划问题,此时模型M可使用规划求解器求解得到符合要求的簇,并进入下一次迭代,如此反复迭代,直至坐标的变化量不再超过给定的阔值θ,即令△a与△b分别为上一代与本代横纵坐标差值,当满足△a≤θ且△b≤θ时,算法终止。算法流程图如图2所示。
3实例分析
本文采用当地一家汽车制造企业的真实数据作为验证及分析算例。该汽车厂在江浙沪地区共有124个客户点,拟建立5个相同规模的配送中心用于服务该区域内的所有客户,并且要求各配送中心之间所处理的客户月物流流量均衡。在此数值实验中,分别采用考虑流量均衡约束的改进K-means算法以及经典的K-means算法进行计算,并對比计算结果。
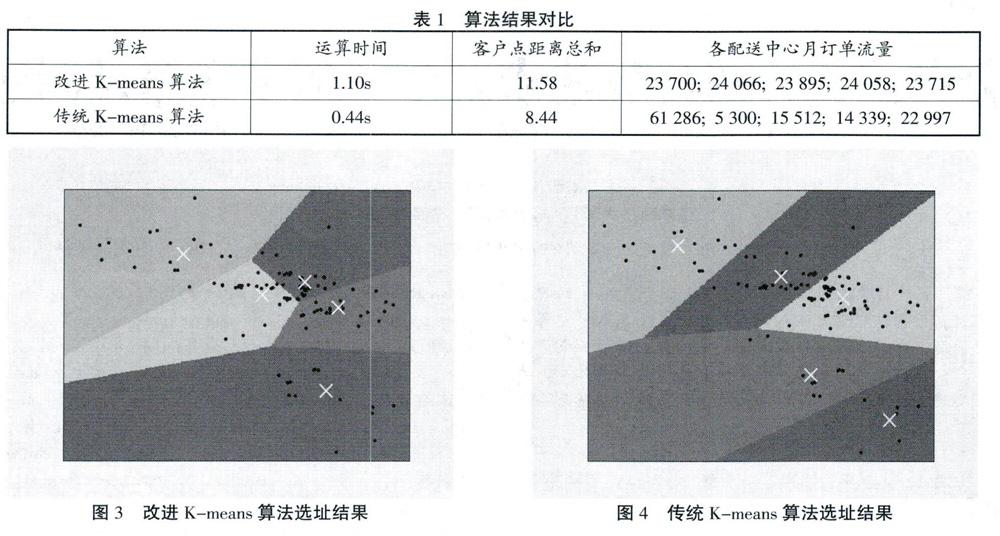
本实验运行于Intel Core i5-7200U(3.1Ghz)和8GB内存的计算机上,并采用CPLEX12.8求解改进K-means算法中的整数规划模型M。实验中坐标变动阈值设为0.005,流量差异阈值设为500。实验结果对比如表1、图3和图4所示(白色标记为配送中心位置):
从实验结果中可以看出,传统K-means算法的客户点距离总和要优于本文的改进K-means算法。其原因在于改进K-means算法需要兼顾流量均衡约束,从而损失了距离上的最优性。从各配送中心月物流流量结果中,可得到两组数据的极差分别为366和55 986。改进K-means算法在控制流量均衡性上要远好于传统K-means算法。在实际物流活动中,若根据传统K-means算法求解得到的结果建造配送中心,则1号配送中心每月需处理订单61286件,而2号配送中心每月只需处理5 300件。由此会造成1号配送中心的物流能力无法匹配其物流流量,而2号配送中心则将处于物流资源闲置的状态。反观改进K-means算法的求解结果,各配送中心的流量较为均衡,避免了上述问题的出现。
4结束语
本文针对多配送中心选址问题,在考虑实际物流活动中流量均衡约束的基础上,构建了该问题的数学模型,并提出一种改进的K-means算法来求解该问题。实验结果表明相较于传统K-means算法,本文算法能够很好地解决流量均衡约束下的多配送中心选址问题。此外,本文的算法框架同样适用于选址问题中的一些其它约束,其拓展性将在今后进行更深入的研究。

