梯形截面斜拉桥竖向涡振分析数值模拟方法比较
张 祥,毛 毳,刘 磊,刘 冲
(天津城建大学土木工程学院,天津300384)
当今桥梁结构逐渐趋向长、细、轻、柔和低阻尼,导致桥对风更加敏感,特别是近地风在低速吹过桥梁时,会发生风的流动分离和周期性的旋涡脱落,使桥面的上下或左右两侧表面出现交替变化的正负压力和力矩,称为涡激力[1].
Pan 等[2]对二维圆柱进行了涡振有限元模拟,得出的涡振模拟结果与风洞试验结果相吻合.刘小兵等[3]通过对分离梯形面双扁平箱梁模型风洞试验的比较,研究了风攻角对其涡振特性的影响.张成龙等[4]对钢桁架桥涡振分析中的三分力系数进行仿真,将模拟三分力系数结果与风洞试验相比较,结果吻合.贾文超等[5]对平板及翼型的涡激振动进行了分析研究,分别比较了二维平板二维翼型及三维梯形翼在单、双向流固耦合下的涡振响应,发现单向求解结果位移响应较大.鲜荣等[6]基于Scanlan 模型,建立涡振模型体系,推导出竖向、扭转涡振的理论近似解并以一实例进行了计算.杨阳等[7]对钢箱梁涡振进行数值模拟分析,发现加大攻角会影响扁平箱梁的扭转涡振,使之更容易发生大范围大振幅扭转涡振.以上学者都对涡振响应进行了数值模拟分析,并得出了对涡振研究有意义的结论.通过对比他们的研究发现,不同的研究对象、不同的数值模拟方法、不同的风攻角均会影响涡振.目前来说,对于桥梁的涡振研究还处在一个基础阶段,还需要进一步探索.
本文使用Ansys 数值模拟平台,以梯形截面大跨度斜拉桥节段模型为研究对象,在低风速下分别通过单、双向流固耦合方法对桥板模型进行涡激振动的有限元分析,计算出从1 m/s 到15 m/s 风速下桥板随时间变化的升力和阻力,比较这两种方法对竖向涡振数值模拟的影响.
1 涡激振动理论
涡激振动是一种限幅振动[8].涡激振动与诸多因素有关:
(1)气动外形.气动外形对涡振影响特别大,当其稍微改变,各自的涡振响应就会大不相同.
(2)湍流特性.描述湍流的参数是湍流强度.通常两者是正相关的,但是某些断面也有例外.
(3)雷诺数.雷诺数的公式如下

式中:v 是流体的运动学黏性系数,是黏性系数与密度的比值.
雷诺数的变化会使流体在尾流区域中产生分离流,称为涡流.在Re 小于5 时,不会发生分离.当Re大于5 之后继续增加时,分离开始发生,分离流变得不稳定并且以特定频率发生涡流脱落[9].
尾流的涡旋脱落频率[10]具有以下关系

式中:D 是横风尺寸;U 是风速;Np是涡旋脱落的频率;S 是斯特劳哈尔数.
在数值模拟中,根据不同风速下的涡脱频率可以反算出S,然后再根据结构的固有频率和S 来估算涡振的起振风速.
从公式(2)可以看出,涡频Np与风速呈线性关系,但发生涡激共振时,涡频会在相当长的风速范围内被结构振动频率所“俘获”,产生一种锁定现象[8].
(4)质量阻尼参数Sc.在涡激振动锁定状态下,结构的振幅和涡振区间受Sc控制,Sc越大,涡振振幅和涡振区间越小.
2 工程背景及有限元模型
2.1 工程背景
离石高架桥是一座矮塔斜拉桥,位于青岛至银川国道的主干线汾阳离石段,是跨越离石市开发区的一座特大斜拉桥,该桥采用的是三跨部分斜拉结构85 m+135 m+85 m,见图1.本文研究该梯形截面斜拉桥主梁节段模型在湍流风场中的竖向涡振响应.主桥横截面尺寸见图2.

图1 主桥立面布置(单位:cm)

图2 主桥截面尺寸(单位:cm)
2.2 节段模型选取依据
风对桥梁结构的作用可以看成是符合片条理论[11]的,这样就可以建立桥梁的节段模型[12]来研究涡振响应.节段模型计算量小,结果准确,省时省力.利用有限元分析软件建成的节段模型,节段模型的高度为3.2 m,桥面宽度为26 m,节段模型长为10 m.流域尺寸为140 m×30 m×10 m,桥板在流域中的位置如图3 所示.空气密度为1.225 kg/m3,混凝土密度为2 300 kg/m3.

图3 桥板模型在流体域的位置(单位:m)
2.3 固体约束与流体边界条件
何新平[13]对该桥成桥模型进行了结构动力特性分析,本文节段模型的实验参数见表1.

表1 节段模型参数
根据结构动力学知识,单自由度振动体系的结构振动圆频率为

故

式中:ω 为结构振动圆频率;k 为弹簧总刚度;m 为等效质量;f 为自振频率.
由式(4)求得竖向弹簧总刚度为3 350.8 kN/m.
在动力自由度关系上,主梁节段模型用三维刚体模拟,结构的竖弯阻尼比设置为0.05,在竖弯自由度上施加4 个弹簧,每个弹簧的刚度为k/4,以获得需要的竖弯自振频率(见图4);在扭转自由度上施加一个扭簧,因为该结构前10 阶模态均未出现扭转模态[13],所以将结构的扭转阻尼比和扭簧刚度设置很大;在侧弯自由度上施加无摩擦约束(frictionless support),限制X 方向的位移,使得侧弯位移始终为0[14].
图4 节段模型弹簧约束示意图
流体域左侧为入口,边界类型为入口边界;右侧为出口,边界类型为开放边界;上下和前后边界均为自由滑移壁面;流固交界面设置为无滑移壁面.
2.4 求解设置
两种方法均采用SST 湍流模型,单向流固耦合采用静网格,双向流固耦合采用动网格,最大循环系数(max.coeff.loops)为100,计算时间为100 s,时间步数为1 000 步.
3 结果和讨论
3.1 升 力
升力为静力三分力之一,其公式如下

式中:Fl为升力;Cl为升力系数;B 为桥宽.
图5 为节段模型在不同风速下升力随时间变化的曲线.

图5 不同风速下升力随时间的变化曲线
对比图5 曲线可以看出,两种方法求得的升力随时间的变化都是迅速减小,随风速增加而增大.不同的是,采用单向流固耦合方法求得的升力在迅速下降之后达到稳定,没有明显的波动;采用双向流固耦合方法求得的升力在风速为1 m/s 时没有出现明显波动,但随风速的增加出现了明显的竖向波动,且风速越大竖向波动越明显,波动的周期越小.
升力的变化会导致桥梁的竖向振动,因此通过前面的分析可以看出,单向流固耦合不利于分析桥梁的竖向振动,即不利于分析桥梁的竖向涡激振动,而双向流固耦合具有较好的分析能力.这意味着在较低的风速下即可较好地显示升力变化,因此在早期阶段可以更好地分析涡激振动.
3.2 阻 力
阻力也是静力三分力之一,其公式如下

式中:Fd为阻力;Cd为阻力系数.
图6 为节段模型在不同风速下阻力随时间变化的曲线.

图6 不同风速下阻力随时间的变化曲线
对比图6 曲线可以看出,两种方法求得的阻力随时间的变化都是迅速减小,随风速增加而增大.不同的是,采用单向流固耦合方法求得的阻力在迅速下降之后呈现周期性波动,随着风速的增加波动一直存在,风速越大波动振幅越大;采用双向流固耦合方法求得的阻力在迅速下降之后变化比较平稳,但随风速的增加会在某一区间范围发生变化,风速越大这种变化的区间越来越多,波动出现的频率越来越高.
对比图5,在5 m/s、10 m/s 和15 m/s 采用双向流固耦合方法得出的阻力值在其升力值下降之后的波谷附近都会发生波动,随着风速的增加,这种变化越来越明显.
3.3 涡脱频率与锁定区间
对升力系数Cl进行傅里叶变换(fft)可以求出各个风速下的涡脱频率Np,根据式(2)可以求出斯特劳哈尔数S.根据涡脱频率随风速变化的关系,可以确定涡振的锁定区间.表2 是不同风速下的涡脱频率与斯特劳哈尔数.
两种方法求得的风速与涡脱频率的锁定现象见图7.
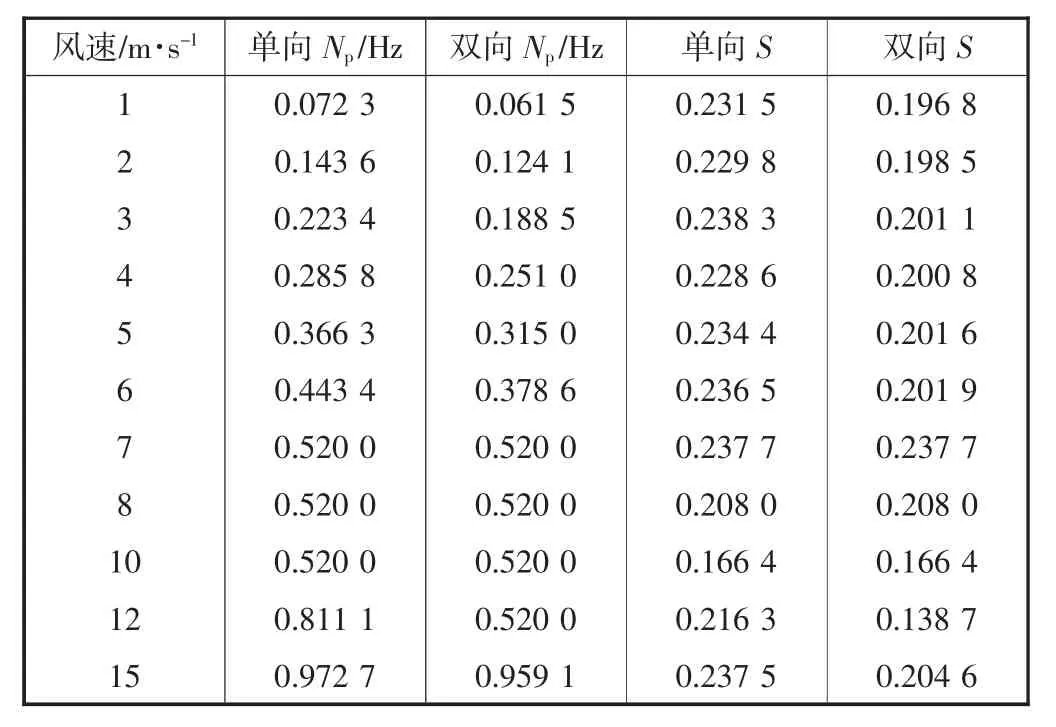
表2 不同风速下的涡脱频率与斯特劳哈尔数

图7 风速与涡脱频率的锁定现象
由风速与涡脱频率的关系可以看出,在风速7 m/s时发生了锁定现象,但是双向方法求得的锁定风速区间较大.推测原因,这是由于双向流固耦合方法中结构的反馈作用,使得结构对风产生反作用,从而抵消了风的一小部分动能,这样一来结构振动“俘获”涡频的风速区间相对变长,与实际相符.
3.4 平板理论验证
Munson 等[15]研究得出平板模型的阻力系数随雷诺数变化关系的理论值,该研究表明流场中物体的阻力系数和雷诺数具有非线性关系.本文为进一步验证两种方法的准确性,分别用两种方法计算了风速从1 m/s 变化到15 m/s 时平板模型的阻力系数以及雷诺数,见表3.
将两种方法得出的结果与Munson 理想平板模型的理论结果相比较,见图8.
对比平板模型理论可以看出,双向流固耦合方法求得的阻力系数在雷诺数Re>8×105时与平板模型理论相近,而单向流固耦合方法求得的阻力系数却与平板理论有着较大的差别.
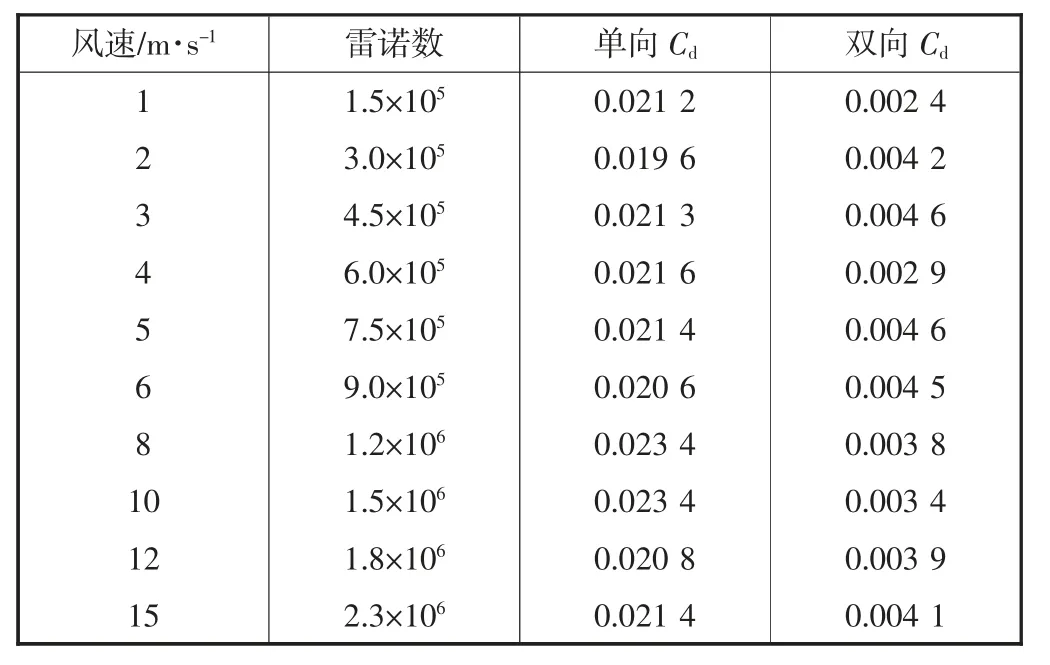
表3 雷诺数与多个风速下的阻力系数Cd

图8 阻力系数随雷诺数变化
4 结 论
(1)采用单向流固耦合方法不利于分析桥梁的竖向涡振,而双向流固耦合方法对升力的变化十分敏感,可以用来分析竖向涡振.
(2)单向流固耦合方法中的升力值大约为相同风速情况下阻力值的3 倍,双向流固耦合方法中,升力值为阻力的2 倍,其原因与动能的耗散有关.
(3)单向流固耦合方法求得的锁定区间为7 m/s 到10 m/s,双向流固耦合方法求得的锁定区间为7 m/s 到12 m/s,双向流固耦合造成的动能耗散是涡振锁定区间变长的重要原因,这是与实际相符的.
(4)通过与平板模型理论比较,可以得出双向流固耦合方法模拟结果更贴近理论值,具有较高的精度.

