ESF算法的截断不可能差分分析*
李明明, 郭建胜, 崔竞一, 徐林宏
信息工程大学, 郑州450001
1 引言
不可能差分分析, 由Knudsen[1]和Biham[2]两人分别独立提出, 是目前常用的密码分析方法之一.其基本思想是排除那些导致概率为0 的区分器的猜测密钥.对于一条概率为0 的差分路径, 当用正确密钥解密密文对时, 不会得到符合该路径的差分; 如果用猜测密钥解密密文对, 得到符合该路径的差分, 则该密钥猜测值是错误的; 那么筛去所有的错误密钥猜测值, 剩下的就是我们需要恢复的正确密钥[3].对一个分组密码算法进行不可能差分分析的先决条件是找到一条概率为0 的差分路径, 即不可能差分区分器.
Kim 等人[4]提出了µ方法, 该方法可以有效找出各种算法结构中所固有的不可能差分形式, 这些固有的不可能差分只与算法的结构有关, 而与算法所采用的S盒无关, 这也就是所谓的截断不可能差分[5].后来 Luo 等[6]在µ方法基础上改进提出了 UID 方法.不同于µ方法, UID 方法利用中间相错的思想将密码算法结构分解成两部分进行处理.此外, 孙兵等[7]基于整环上的矩阵论, 证明了 SPN 结构及嵌套SPN 的Feistel 结构的截断不可能差分区分器的上界取决于线性层的本原指数.
ESF 算法[8]是2013 年刘宣等人基于LBlock 算法[9]改进的的轻量级分组密码算法, 其置换层借鉴PRESENT 算法[10]中P置换的形式, 能够使得在较少的轮数中快速扩散, 从而达到增加密码算法抵抗攻击的安全性.该算法分组长度为 64-bit, 密钥长度为 80-bit, 整体采用变形 Feistel 结构, 由非线性变换S盒、P置换、循环移位、异或四种运算组成.
目前, 对于 ESF 算法有多个安全性分析结果.徐朋[11]给出了 ESF 算法的差分故障攻击, 尹军等人[12]给出了 ESF 算法的 13 轮相关密钥差分分析.而ESF 算法的不可能差分分析结果相对较多, 最初刘宣等人[13]给出了 ESF 算法一条 8 轮不可能差分区分器, 并给出了 11 轮不可能差分分析, 之后陈玉磊等人[14]基于同一条 8 轮不可能差分区分器改进了 ESF 算法的 11 轮不可能差分分析结果; 高红杰等人[15]也基于同一条8 轮不可能差分区分器, 并根据密钥之间的关系, 给出了ESF 算法的12 轮不可能差分分析.
本文首先给出了ESF 算法的一些新的8 轮截断不可能差分区分器.其次, 基于得到的8 轮不可能差分区分器, 并利用密钥编排算法部分子密钥间存在的依赖关系, 给出了对ESF 算法的13 轮不可能差分分析, 恢复了 80 比特主密钥, 时间复杂度为 277.39次 13 轮 ESF 算法加密, 数据复杂度为 261.99个选择明文.
2 ESF 算法介绍
本节主要对文章里出现的符号进行说明及介绍ESF 算法的基本知识.首先给出符号说明如下.
Li第i+1 轮输入的左半分组
Ri第i+1 轮输入的右半分组
∆Li两个输入Li和的差分
∆Ri两个输入Ri和的差分
<<<α循环左移α比特
Ki第i+1 轮子密钥
Ki−jn第n+1 轮子密钥的i到j比特
Li[j]表示Li的第j比特
∆Li[j]表示 ∆Li的第j比特
[i]2轮常数i的二进制表示
∗不确定的比特差分
∥二进制字符连接
ESF 轻量分组密码算法采用变形Feistel 结构, 其分组长度为64-bit, 密钥长度为80-bit, 迭代轮数为32 轮.该算法加密流程如图1 所示, 其中轮函数F由子密钥异或、非线性变换S盒、P置换组成, 为典型 SPN 结构, 具体可表示为F(Ri,Ki)=PS(Ri⊕Ki).
ESF 算法中的非线性变换S盒、P置换及密钥编排算法具体介绍如下.
非线性变换S 盒ESF 算法的非线性变换由8 个对合4 比特S盒组成,即S=(S1,S2,S3,S4,S5,S6,S7,S8), 其中Si:{0,1}4→ {0,1}4,i=1,2,··· ,8.
P 置换P置换将 32 比特的顺序进行重新排列.P: (b1,b2,··· ,b32) → (c1,c2,··· ,c32), 其中当0 ≤i≤ 7 时, 有 (b4i+1,b4i+2,b4i+3,b4i+4) → (ci+1,ci+9,ci+17,ci+25).

图1 ESF 系列算法轮函数Figure 1 Round function of ESF
密钥编排算法ESF 算法主密钥长度为 80 比特, 密钥扩展设计与 LBlock 算法类似.将主密钥K=k79k78···k1k0存入密钥寄存器, 每一轮取寄存器最左端32 比特作为子密钥.对于0 ≤i≤31 , 扩展算法可表述为
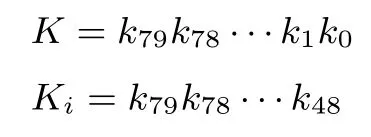
在得到第i轮子密钥Ki−1后, 按如下步骤更新密钥寄存器K
(1)K<<<13;
(2) [k79k78k77k76]←S0[k79k78k77k76], [k75k74k73k72]←S0[k75k74k73k72];
(3) [k47k46k45k44k43]←[k47k46k45k44k43]⊕[i]2;
(4) 取当前密钥寄存器K最左端32 比特作为子密钥Ki.
3 ESF算法的8轮截断不可能差分区分器
本节首先介绍 ESF 算法的相关性质, 其次根据这些性质给出ESF 算法的一些新的 8 轮截断不可能差分区分器.
性质 1S盒的输出差分不为零当且仅当其输入差分不为零.
性质 2对于ESF 算法任意不可能差分区分器, 如果比特矛盾出现在分组的左半部分, 则分组的右半部分也必存在矛盾, 反之亦然.
证明:不妨设加密方向差分路径 (∆Li,∆Ri) → (∆Li+s,∆Ri+s) 以概率 1 成立, 解密方向差分路径 (∆Lj−t,∆Rj−t)←(∆Lj,∆Rj) 也以概率 1 成立, 且则可知 (∆Li,∆Ri) ↛(∆Lj,∆Rj) 是一条s+t轮不可能差分区分器.
由于 ESF 算法是变形 Feistel 结构,有Lk+1=Rk<<<7,故 ∆Li+s= ∆Ri+s−1<<<7,∆Lj−t=∆Rj−t−1<<<7 .从而当且仅当
根据性质1 和性质2, 发现了一些新的8 轮截断不可能差分区分器, 如定理1 所示.
定理 1当初始输入状态差分满足 (∆L1,∆R1) = (a1a2a3a41a5a6a70000 0000 0000 0000 0000 0000, 0000 0000 0000 0000 0000 0000 0000 0000), 其中a1,a2,a3,a4,a5,a6,a7为任意值, 经 8 轮ESF 算法加密后输出状态差分满足 (∆L9,∆R9) = (0000 0000 0000 0000 0000 0000 0000 0000,0000 0000 0000 0000 0000 0000 0000 1000) 是不可能的.具体形式如图2 所示, 其中bi/di/ei/fi/gi/hi,i∈ {1,2,3,···} 皆不全为 0.

图2 ESF 算法的8 轮不可能差分区分器Figure 2 8-round impossible differential distinguisher of ESF
证明:当初始输入状态差分满足 (∆L1,∆R1) = (a1a2a3a41a5a6a70000 0000 0000 0000 0000 0000, 0000 00000000 0000 0000 0000 0000 0000) 时, 初始输入状态 (L1,R1) 经 3 轮 ESF 算法加密后输出差分满足 ∆R4= (d1⊕a70d50d90d130d20d60d100d140d30d70d110d150d4a1d8⊕a2a3d12⊕a41d16⊕a5a6).由于故由性质 1 可知s8(d12⊕a41d16⊕a5a6) = (e29e30e31e32)(0000).(L4,R4) 再经 1 轮 ESF 算法加密后输出差分满足 ∆R5(e1e5⊕b2e9⊕b6e13e17e21e25e29e2e6⊕b3e10⊕b7e14e18e22e26e30e3e7⊕b4e11⊕b8e15e19e23e27e31e4e8⊕b1e12⊕b5e16e20e24e28e32) .
而当初始输出状态差分满足 (∆L9,∆R9) = (0000 0000 0000 0000 0000 0000 0000 0000, 0000 0000 0000 0000 0000 0000 0000 1000), (L9,R9) 经 4 轮 ESF 算法解密后输出差分满足 ∆R5=(f40f80f120f160f10f5⊕10f90f130f20f60f100f140f30f70f110f150).由于 (e29e30e31e32)(0000),故(e1e5e9e13e17e21e25e29e2e6e10e14e18e22e26e30e3e7e11e15e19e23e27e31e4e8e12e16e20e24e28e32)(f40f80f120f160f10f5⊕10f90f130f20f60f100f140f30f70f110f150), 从而产生矛盾, 所以结论成立.
除定理1 中的不可能差分区分器外, 还找到了如下 ESF 算法的 8 轮截断不可能差分区分器, 其中ai(1 ≤i≤15) 为任意值,b1,b2,b3不全为 0,c1,c2,c3,c4也不全 0.

4 ESF算法的13轮不可能差分分析
利用定理1 给出的 8 轮不可能差分区分器, 向上解密 2 轮, 向下加密 3 轮, 得到 ESF 算法的 13 轮不可能差分路径, 如图3 所示, 其中a1,a2,a3,a4,a5,a6,a7为任意值,bi/ci/di/ei/fi,i∈ {1,2,3,···} 皆不全为0.

图3 ESF 算法的13 轮不可能差分路径Figure 3 13-round impossible differential cryptanalysis of ESF
性质 3若已知子密钥K12, 便可推导出主密钥k3,k2,k1,k0,k79,··· ,k54及子密钥的值; 若已知子密钥可推导出主密钥k4.
证明:密钥寄存器更新算法由循环移位、非线性变换S盒、常数异或三种变换组成.由于常数异或变换为线性变换且常数值已知, 其逆运算只需在对应位置异或同一个常数即可, 为叙述简洁, 故不考虑密钥编排算法中使用的常数异或变换.
密钥比特位置的更新由循环移位变换决定.若不考虑S盒, 根据密钥编排算法中的循环移位变换, 可得各轮子密钥与其对应原始主密钥之间关系, 如表1 所示.攻击过程中需要猜测的子密钥与其对应原始主密钥之间关系, 如表2 所示.

表1 各轮子密钥与其对应原始主密钥之间关系Table 1 Relationship between each round key and its corresponding original master key

表2 需要猜测的子密钥与其对应原始主密钥之间关系Table 2 Relationship between guessed subkey and its corresponding original master key
由于密钥编排算法中采用的移位数13 不是4 的倍数, 会打乱半字节块内的顺序.故需进一步分析S盒对子密钥与对应原始主密钥比特之间关系的影响.根据密钥编排算法, 可得如下密钥关系

由上可知, 若已知子密钥K12, 可逆推导出子密钥及主密钥k3,k2,k1,k0,k79, ··· ,k54的值.又因为K0=k79k78···k48, 故进一步得出子密钥同样若已知子密钥可推导出主密钥k4.
利用子密钥之间的依赖关系, 可大大减少攻击过程中需要猜测的总密钥数, 现只需猜测 48 比特子密钥结合早夭技术 (early abort technique)[16], ESF 算法的 13 轮不可能差分攻击过程具体如下.
(1) 选择 2n个明文结构, 其中的明文满足L0[1,3,5,7,9,11,13,19,23,25,27,29,31],R0[4,5,6,7,8,12, 13,14,15,16, 20,21,22,23,24,28,29,30,31,32]取定值, 其余比特取任意值, 故一个明文结构包含231个明文, 可以构造261个明文对.因此攻击的选择明文量为2n+31, 其中包含2n+61个明文对.这些明文对经13 轮ESF 加密可得2n+61个密文对.
(2) 筛选出满足如下差分的密文对 ∆L13= (e130e20e60e100e140e30e70e11⊕10e150e40e80e120e160e10e50e90), ∆R13=(f1⊕d1f5f9f13f17f21f25f29f2⊕d2f6f10f14f18f22f26f30f3⊕d3f7f11f15f19f23f27f31f4⊕d4f8f12f16f20f24f28f32).经这一步筛选后平均剩余 2n+61×2−16=2n+45个数据对.
(3) 猜测第 13 轮子密钥K12.对于剩余的数据对, 筛选出差分满足 ∆L12=(d1000 0000d2000 0000d3000 0000d4000 0000) 的数据对, 其中R12=L13>>> 7,L12=PS(R12⊕K12)⊕R13, 经这一步过滤大约剩余 2n+45×2−28= 2n+17个数据对.这一步骤使用 “早夭技术”, 分步猜测密钥筛选数据对.首先猜测密钥部分解密第 13 轮变换, 判断 ∆L12第 8, 16, 24, 32 比特是否都为 0, 利用此条件筛除不符合要求的数据.对保留下来的数据对再猜测判断 ∆L12第 7, 15, 23, 31 比特是否都等于 0, 筛除不符合要求的数据对.以此类推, 最后猜测不同于前 7 个半字节的密钥猜测的是, 因为 ∆L12第 1, 9, 17, 25 比特为不确定差分, 故无需筛选数据对.从而, 这一步骤总的计算量约为2×(2n+45×24+2n+41×28+2n+37×212+···+2n+21×228+2n+17×232)/8 =2n+50次一轮加密运算.
(4) 已知第 13 轮子密钥K12的取值, 由密钥编排算法可推导出故对于(L12,R12) 向上解密一轮, 只需猜测子密钥即可.对于剩于数据对, 筛选出差分满足∆L11=(0000 0000 0000 0000 0000 0100 0000 0000) 的数据对.这一步骤同样使用 “早夭技术”, 分步猜测密钥筛选数据对.首先根据推导出的判断 ∆L11[6,14,22,30,8,16,24,32]=(00100000) 是否成立, 利用此条件筛除不符合要求的数据对.其次猜测子密钥判断∆L11[2,10,18,26,4,12,20,28]= (00000000) 是否成立, 进一步删选不符合要求的数据对.经这一步过滤大约剩余2n+17×2−16=2n+1个数据对, 其计算量约为2×(2n+17×232+2n+9×232×28)/4=2n+49次一轮加密运算.
(5) 已知第 13 轮子密钥K12的取值, 由密钥编排算法可推导出根据推导出的判断∆L10的第8, 16, 24, 32 比特是否全为0, 利用此条件筛除不符合要求的数据对.经这一步过滤大约剩余 2n+1×2−4=2n−3个数据对, 其计算量约为 2×(2n+1×232×28)/8=2n+39次一轮加密运算.
(6) 已知第 13 轮子密钥K12的取值, 由密钥编排算法可推导出故对于 (L0,R0) 向下加密一轮, 只需猜测子密钥K25−280即可.对于剩余的数据对, 筛选出差分满足∆R1=(0000 000a1a2a3a41a5a6a700000 0000 00000000) 的数据对, 其中R1=PS(R0⊕K0)⊕L0<<< 7, 经这一步过滤大约剩余 2n−3× 2−12= 2n−15个数据对.这一步骤的计算量约为2×2n−3×232×28×24÷2=2n+41次一轮加密运算.
(7) 已知第 13 轮子密钥K12的取值, 由密钥编排算法可推导出故对于 (L1,R1)向下加密一轮, 只需猜测子密钥即可.这一步骤同样使用 “早夭技术”, 分步猜测密钥筛选数据对.首先根据推导出的判断 ∆R2[2,10,18,26,3,11,19,27]= (00000000) 是否成立,利用此条件筛除不符合要求的数据对, 平均剩余 2n−15× 2−8= 2n−23.其次猜测子密钥判断 ∆R2[4,12,20,28]= (0000) 是否成立, 经该半字节解密后以 2−4的概率得到不可能差分区分器的输入, 此时所猜测的密钥是错误密钥.这一步总的计算量约为2×(2n−15×232×28×24÷4+2n−23×232×28×24×24÷8)≈2n+28次一轮加密运算.
定理 2利用8 轮不可能差分区分器对13 轮ESF 算法进行不可能差分分析, 恢复80 比特主密钥, 其时间复杂度为277.39次13 轮ESF 算法加密, 数据复杂度为261.99个选择明文.
证明:上述攻击过程中, 共猜测了 48 比特子密钥, 经第 7 步排除错误密钥后大约剩余ε=248×(1 − 2−4)2n−23个候选密钥.由子密钥可得 31 比特主密钥k4,k3,k2,k1,k0,k79,··· ,k54,故经第 7 步排除错误密钥后, 主密钥k4,k3,k2,k1,k0,k79,··· ,k54剩余ε种可能取值.再穷举恢复k4,k3,k2,k1,k0,k79,··· ,k54这ε种可能取值和剩余 49 比特主密钥, 便可唯一确定主密钥, 其计算量为ε×249.攻击过程中的时间复杂度主要集中在第3 步, 故当n≈30.99 时, 13 轮ESF 算法不可能差分分析总时间复杂度约为 2n+50/13+ε× 249= 2n+50/13+248× (1 −2−4)2n−23×249≈ 277.39次 13 轮ESF 算法加密, 数据复杂度为231+30.99=261.99个选择明文.
5 结论
本文首先给出了ESF 算法的一些新的8 轮截断不可能差分区分器.其次, 基于得到的8 轮不可能差分区分器, 并利用密钥编排算法部分子密钥间存在的依赖关系, 给出了对ESF 算法的13 轮不可能差分分析, 恢复了 80 比特主密钥, 时间复杂度为 277.39次 13 轮 ESF 算法加密, 数据复杂度为 261.99个选择明文.本文给出的ESF 算法不可能差分分析结果与现有结果对比, 如表3 所示, 其中 ID 表示不可能差分分析.
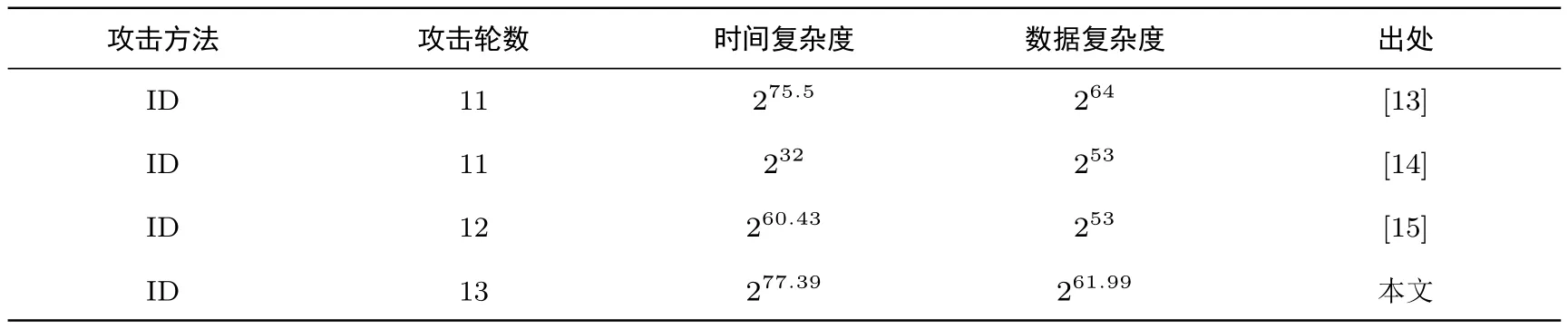
表3 ESF 算法的不可能差分分析结果对比Table 3 Comparison of impossible differential attacks on ESF

