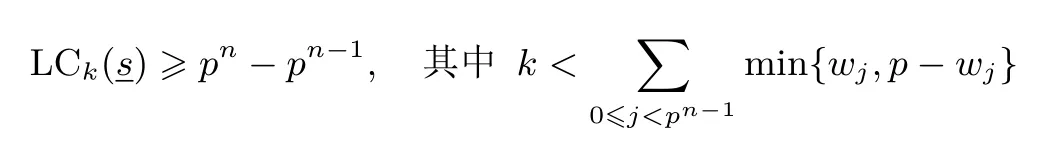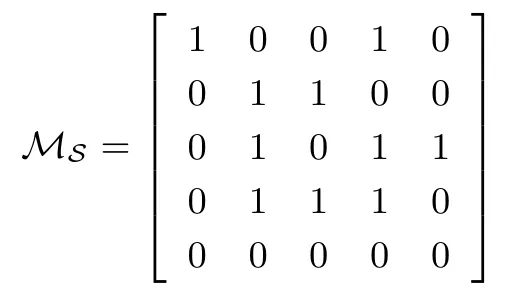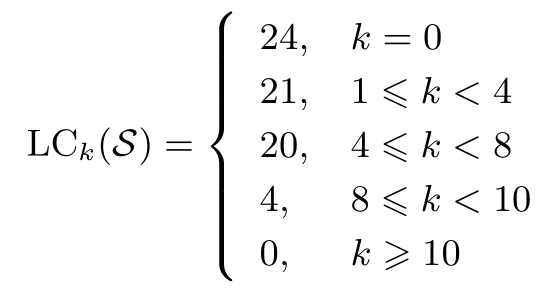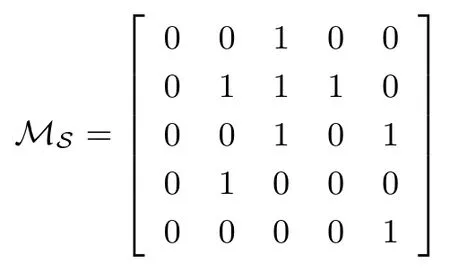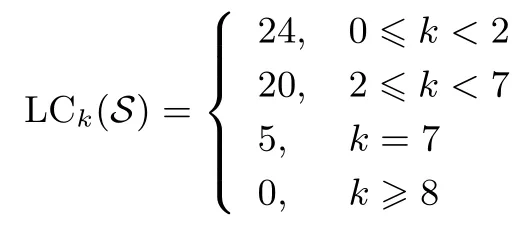周期为素数平方的二元序列的k-错线性复杂度*
陈智雄, 牛志华, 吴晨煌,3
1.莆田学院应用数学福建省高校重点实验室, 莆田351100
2.上海大学计算机工程与科学学院, 上海200444
3.电子科技大学计算机科学与工程学院, 成都611731
1 引言
伪随机序列在通信、密码学等领域具有广泛的应用, 如在序列密码中, 密文序列是由明文序列与密钥序列异或得到, 其安全性完全依赖于密钥序列的随机性.因此密钥序列的设计及其密码学指标是关键的研究方向, 序列的密码学指标主要包括: 平衡性、相关性、线性复杂度及其稳定性, 等等[1–3].首先介绍序列的线性复杂度、k-错线性复杂度的概念.
设F2= {0,1} 为二元有限域, 对于F2上周期为T的二元序列其线性复杂度(记为定义为满足F2上的如下线性递归关系的最小阶L
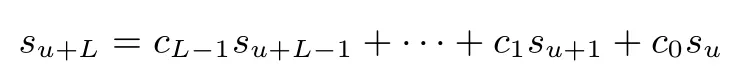

S(X)被称为的生成多项式.那么,在F2上的线性复杂度可通过下式计算
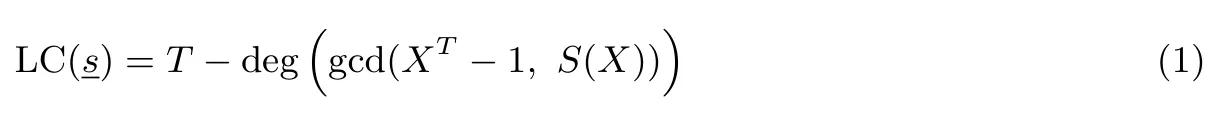
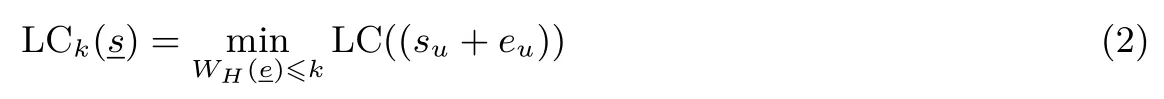
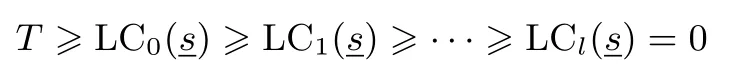
线性复杂度和k-错线性复杂度是序列的重要密码学性质, 它们刻画的是序列的可预测性从而衡量该序列是否适用于密码学领域.从密码学应用角度来说, 一个序列的线性复杂度应尽可能的大, 并且序列在改变若干项后其线性复杂度不应明显降低[1,2].
早在 1969 年, Massey 设计了一个算法用于计算序列的线性复杂度[5], 往后的文献中称之为 BM 算法.1983 年, Games 和Chan[6]给出了周期为2n的二元序列的线性复杂度的快速算法, 算法的时间复杂度远低于通用的 BM 算法.1993 年, Stamp 和 Martin[4]对 Games-Chan 算法进行了扩展, 引入一维代价数组, 提出了周期为2n的二元序列的k-错线性复杂度的快速算法.
本文我们主要讨论周期为奇素数幂pn的二元序列的线性复杂度与k-错线性复杂度问题.为了综述的方便, 我们设是 F2上周期为pn的二元序列, 并将s的一个周期表示为矩阵的形式

1999 年, 魏仕民等[7]将Games-Chan 算法进行了扩展, 提出了周期为pn的二元序列的线性复杂度的快速计算算法, 其基本思想是一个迭代计算算法, 首先将上述矩阵中的每一行相加得到一个周期为pn−1新序列那么的线性复杂度可写成

其中, 如果上述矩阵的每一行都相同, 则δ=0, 否则δ=1.接着按照这个思想考虑序列的线性复杂度.
2001 年, 王磊等[8]基于从 Games-Chan 算法到 Stamp-Martin 算法的思想, 扩展了文献 [7]中的算法, 提出了周期为pn的二元序列的k-错线性复杂度的快速算法, 在计算中也是考虑序列所对应的矩阵形式的行结构.需要说明的是, 魏仕民等[7]与王磊等[8]的算法中, 都要求 2 是模p2的一个本原根, 即2 模p2的乘法阶为(p−1)p.
我们将从另一个角度来讨论序列的线性复杂度与k-错线性复杂度, 也就是我们考虑上述矩阵形式(3)的列结构, 通过每一列的重量(即每一列所含1 的个数) 分布情况来确定序列的线性复杂度与k-错线性复杂度的取值.为了理解上的方便, 我们只考虑周期为p2的二元序列, 记为S=(s0,s1,··· ,sp2−1), 其一个周期的矩阵形式为

我们将通过考察MS的结构, 更准确地说, 我们应用MS的列重量即可确定二元序列S的线性复杂度及k-错线性复杂度.第2 节给出一般性结果, 第3 节讨论两类特殊的序列, 第4 节总结并提出进一步研究的问题.
2 k-错线性复杂度: 一般性结论
我们先定义几个参数.设wj=wt(Mj) 表示上节式 (4) 矩阵MS的列Mj的重量 (即向量Mj中 1的个数).记二元序列S=(s0,s1,··· ,sp2−1) 的生成多项式为S(X) 及
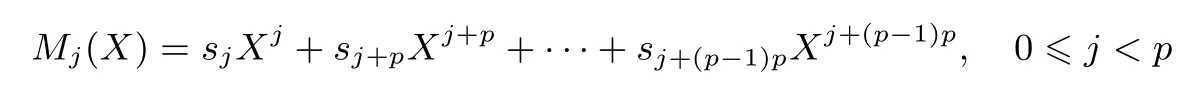
引理 1设S= (s0,s1,··· ,sp2−1) 是 F2上周期为p2的二元序列, 其矩阵表示形式为MS=[M0,M1,··· ,Mp−1],S(X) 为S的生成多项式, 则有
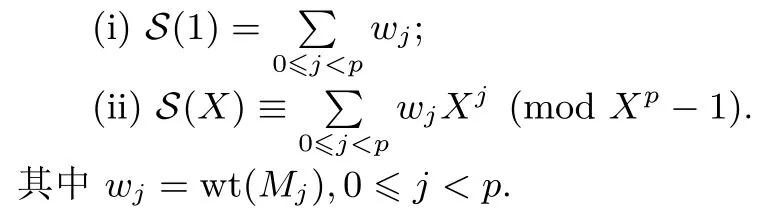
证明:(i) 显然; (ii) 从Mj(X)≡wjXj(modXp− 1) 即得.
我们需要事先做一个说明, 如果序列S的矩阵形式MS= [M0,M1,··· ,Mp−1]中, 所有列或为全 0列 (0,0,··· ,0)T或为全 1 列 (1,1,··· ,1)T, 那么 (1+Xp+X2p+ ···+X(p−1)p)|S(X), 从而S的线性复杂度LC(S)p.因此下文中我们总假设MS至少有一列不是全0 列或全1 列.
定理 1设S= (s0,s1,··· ,sp2−1) 是 F2上周期为p2的二元序列, 其矩阵表示形式为MS=[M0,M1,··· ,Mp−1],S(X) 为S的生成多项式.对于wj= wt(Mj),0j 如果 2 模p2为本原元, 那么当S(1)≡0 (mod 2) 时, 我们有 而当k⩾κ3时, LCk(S)p. 证明:由于2 模p2为本原元, 我们得到 是既约分解, 令 Φ1(X)=1+X+X2+ ···+Xp−1, Φ2(X)=1+Xp+X2p+ ···+X(p−1)p. 其中Ek是周期为p2的二元错误序列且在一个周期内仅含有k个 1.设新序列Sk与错误序列Ek的生成多项式分别记为Sk(X) 与Ek(X), 那么Sk(X)=S(X)+Ek(X).下面我们讨论使得Φ1(X)|Sk(X) 或Φ2(X)|Sk(X) 成立的最小k. 首先考察当k满足什么条件时可以保证Φ1(X)|Sk(X).由引理1 知 其次考察当k满足什么条件时可以保证 Φ2(X)|Sk(X).如果存在h(X) =h0+h1X+ ··· +hp−1Xp−1(次数 那么我们得到 从上面讨论, 并注意到κ1κ3, 那么当κ0+κ2<κ1时, 当k<κ0+κ2时, 对任何的Ek(X) 都不能保证 Φ1(X)|Sk(X); 当k<κ1时, 对任何的Ek(X) 都不能保证 (Xp− 1)|Sk(X); 当k<κ3时, 对任何的Ek(X) 都不能保证Φ2(X)|Sk(X), 故我们证明了第一个结论. 而当κ0+κ2>κ1时, 情况更为简单.当k<κ1时, 对任何的Ek(X) 都不能保证 (Xp−1)|Sk(X);当k<κ3时, 对任何的Ek(X) 都不能保证Φ2(X)|Sk(X), 我们就证明了第二个结论. 而当kκ3时, 我们能找到合适的Ek(X) 使得 Φ2(X)|Sk(X), 从而 LCk(S)p. 在定理1 的条件下, 如果S(1)≡1 (mod 2), 情况可以类似讨论, 结果如下. 定理 2设S= (s0,s1,··· ,sp2−1) 是 F2上周期为p2的二元序列, 其矩阵表示形式为MS=[M0,M1,··· ,Mp−1],S(X) 为S的生成多项式.对于存在某个j0使得0 如果 2 模p2为本原元, 那么当S(1)≡1 (mod 2) 时, 我们有 (i) 若κ0+κ2=0 (也即κ1=p), 则有 我们在附录中, 列举了2 个例子, 并借助文献[8]中的算法通过计算机程序运行, 验证结果与上述定理一致. 下一节讨论文献中研究较多的两类序列: 广义割圆序列与交织序列.在一些特殊条件下, 它们的k-错线性复杂度取值更为直观. Kim 与 Song[9]利用模pn剩余类环构造广义割圆序列, 根据我们的需要, 这里限定n= 2.设e=(p−1)/2 及g模p2为本原元.定义广义割圆类 其中j=0,1.注意到模p2剩余类环 Zp2满足 即可定义周期为p2的二元平衡的广义割圆序列C=(c0,c1,··· ,cp2−1) 如下: 引理 2设v∈ {1,2,··· ,p− 1}. (i) 有 (p− 1)/2 个v使得另外 (p− 1)/2 个v使得 (ii) 对于j=0,1, 如果则对任意的 0i 证明:(i) 从即得.(ii) 设v+ip≡g2m+jmodp2,那么v≡v+ip≡g2m+jmodp, 故结论成立. 将序列C写成矩阵的形式MC, 从引理2 可以看出, 该矩阵的第 1 列含有 (p+1)/2 个 1, 第 2 列至第p列中有 (p−1)/2 列是全 0 的列, 剩下的 (p−1)/2 列是全 1 的列.于是我们得到下面的结论. 定理 3设C=(c0,c1,··· ,cp2−1) 是如式 (5) 所定义的周期为p2的二元广义割圆序列, 如果 2 模p2为本原元, 我们有 从定理3看, 只需改变(p−1)/2 项, 其线性复杂度就会引起急剧降低, 而且从该序列的矩阵形式看, 有p−1 列是全0 列或全1 列, 这种分布也是很糟糕的, 因此该序列不是好的伪随机序列.事实上, 从MC的结构即可看出, 对任何的素数p(2 模p2未必是本原元), 恒有 LC(p−1)/2(C)p.但最近几年研究的另一类序列, 它的构造与费马商有关, 具有很好的密码学性质, 见文献[10–13]. 先介绍交织序列的构造.周期为p的二元序列对于整数i, 左移操作Li定义为并记如果第 1 节中式 (4) 所列的序列S的矩阵MS, 其每一列Mj都可以写成如下形式: 其中对每一个j:0,1,··· ,p− 2,ej∈ {0,1,··· ,p− 1} 且ep−1= ∞.于是就称序列S为一个周期为p2的交织序列 (interleaved sequence), 而序列是构造S的基序列 (base sequence).如果选取另一个周期为p的二元序列在S的基础上, 可以构造交织序列簇如下,它总共含有p+1 个序列 MU(r)的列形如 对于交织序列的一般构造, 有兴趣的读者可参见文献[2,14,18].文献[15,16]研究了均为Legendre序列时的交织序列的平衡性、相关性等问题. 为简便起见, 我们仅讨论序列U(p)的k-错线性复杂度问题, 而其它序列U(0),U(1),··· ,U(p−1)的k-错线性复杂度问题在讨论方法上是类似的. 定理 4设是 F2上周期为p2的二元交织序列, 其矩阵表示形式为其中是周期为p的二元序列且在一个周期内含有 1的个数记为w, 对 0jp− 2,ej∈ {0,1,··· ,p− 1}.不妨假设 1w(p− 1)/2, 那么在 2 模p2为本原元时, 我们有 证明:记U(p)的生成多项式为U(p)(X), 我们发现 那么当w为偶数时, 有(Xp−1)|U(p)(X), 所以LC0(U(p))=p2−p.另一方面, 我们考虑U(p)在一个周期内改变k比特后, 使得 (1+Xp+X2p+···+X(p−1)p)|(U(p)(X)+Ek(X)), 其中Ek(X) 是一个含有k项且次数小于p2的多项式.为此, 只有把U(p)的矩阵形式的每一列都变为全 0 列或全 1 列, 才能实现.注意到w(p−1)/2, 易知最小的k= (p−1)w, 且此时可以把U(p)变为一个全 0 序列, 故有 LC(p−1)w(U(p))=0. 当w为奇数时,U(p)(1)=0 但 (1+X+ ···+Xp−2+Xp−1) ∤U(p)(X) 且 (1+Xp+X2p+ ···+X(p−1)p) ∤U(p)(X), 故 LC0(U(p)) =p2− 1.从式 (8) 知, 只需增加一项Xp−1, 即可保证 (1+X+···+Xp−2+Xp−1)|(U(p)(X)+Ek(X)), 那么只需在MU(p)的最后一列增加k= 1 比特即可实现, 故LC1(U(p)) =p2−p+1.再根据式 (8), 在MU(p)的前p−1 列每列增加或减少 1 个比特即可即可保证(Xp−1)|(U(p)(X)+Ek(X)), 这时k=p−1, 故 LCp−1(U(p))=p2−p.其它情况与上面的讨论类似. 从应用的角度, 当然选择w= (p−1)/2, 可以保证序列的 0,1 分布基本达到均衡.如取p= 11, 当是周期为 11 的 Legendre 序列 (01011100010) 时, 我们随机选取移位值e0,e1,··· ,ep−2得到周期为 121的交织序列U(11), 于是我们可以得到并运用算法验证下面结果: 与定理4 结论一致. 我们分析了周期为素数平方p2的二元序列的线性复杂度与k-错线性复杂度, 通过序列的矩阵表示的列重量即可得出相关的结论, 无需通过设计算法进行计算.本文的方法可以推广到周期为pn(n> 2)的二元序列事实上只需按照文献 [7,8]中算法的思想, 将序列的矩阵 (3) 的每一行相加得到周期为pn−1的新序列, 考虑新序列的k-错线性复杂度问题, 由此进行迭代计算.简言之, 记序列的矩阵(3) 的第j(0j 本文的结果也是在 2 模p2是本原根的条件下成立, 但对于 2 模p2不是本原根时, 也是值得研究的问题. 附录 例 1.设p=5, 如果取周期为 25 的二元序列S的矩阵形式为 那么定理1 中的参数κ0=0,κ1=4,κ2=1,κ3=8, 满足κ0+κ2<κ1, 应用算法 [7]通过运行程序得到 如果取周期为25 的二元序列S的矩阵形式为 那么参数κ0=1,κ1=2,κ2=2,κ3=7, 满足κ0+κ2>κ1, 应用算法 [7]通过运行程序得到 验证结果符合定理1.我们也进一步选择不同的p对定理1 与定理2 所有可能的情况加以验证, 结论都是一致的. 例 2.设p=3, 取周期为27 的二元序列S的矩阵形式为 从MS的列可以看出, 第 0, 3, 8 列的 0 改为 1, 第 1, 4, 5, 6 列的 1 改为 0, 共需改变 7 个比特, 可得 LC7(S)9(=p2), 而 LC6(S) ⩾ 18(=p3−p2).当矩阵的第 1, 4, 5, 6, 7 列各改变一个比特(即共改变 5 个比特) 使得每一列的重量为偶数时, 改变后的序列的生成多项式≡0 (modXp2−1), 故LC5(S)=18=LC6(S).
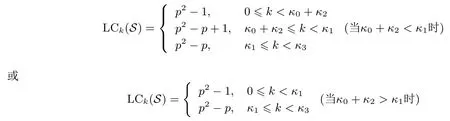
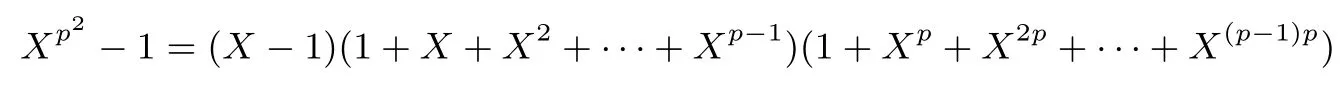


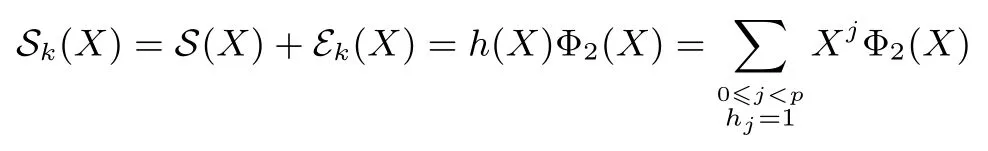
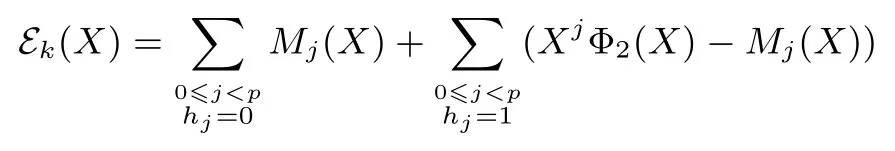
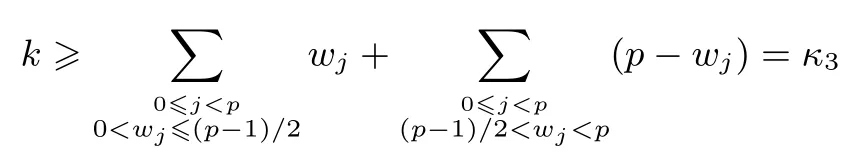



3 k-错线性复杂度: 两类特殊序列
3.1 周期为p2的广义割圆序列

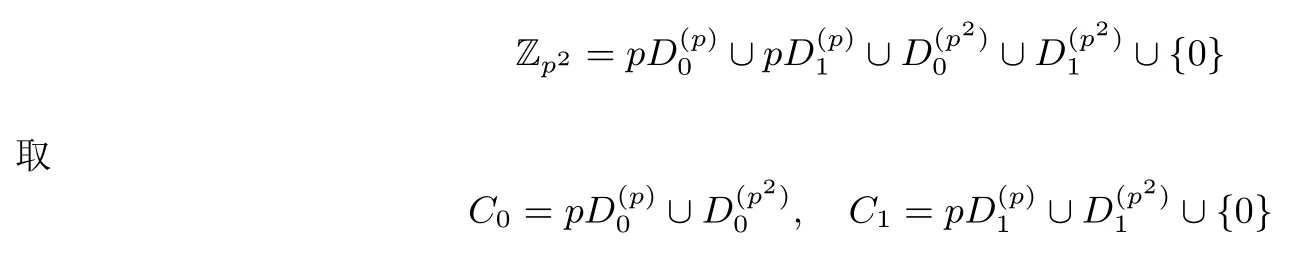


3.2 周期为p2的交织序列
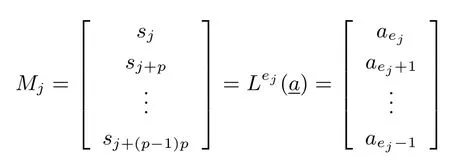

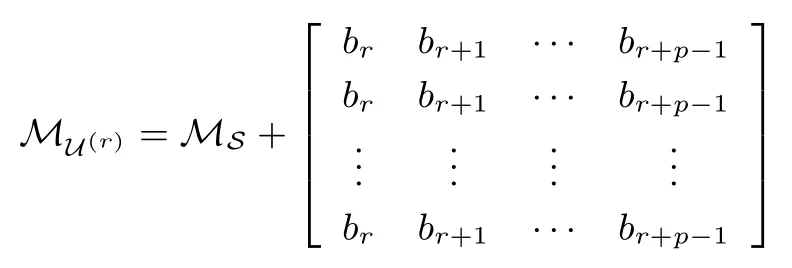
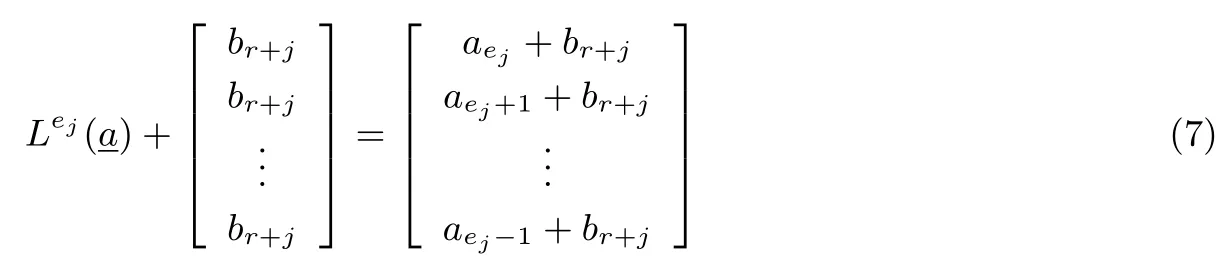
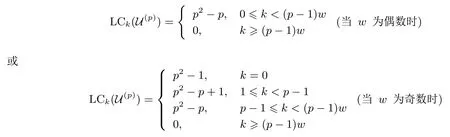

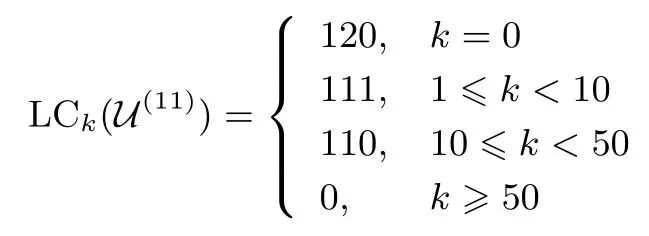
4 结束语