关于驻波的瞬态能量传输问题的探讨

张荣利

(黄石市第十六中学 湖北 黄石 435002)

刘红日

(湖北师范大学物理与电子科学学院 湖北 黄石 435002)

驻波是一类特殊的干涉现象.当两列频率相同、振动方向相同、振幅相等,相差恒定的波在同一直线上沿相反方向传播时就会在叠加区域产生驻波.驻波在力学、电磁学、光学等领域有重要的应用.根据维度不同，驻波可以分为一维驻波、二维驻波和三维驻波[1]，根据振动的物理量不同可以分为机械驻波和电磁驻波等.驻波的主要特点是波形位置固定，相邻波节之间分段振动而总能量不变.虽然各段之间没有能量传播，但是各段内部存在瞬态能量传递.虽然关于驻波的能量问题已经有很多研究[2,3]，但是关于驻波内部瞬态能量传播的讨论较少[4].以机械驻波为例，瞬态能量传播与波线上质元的位移以及能量变化直接相关.只有从质元的位移和形变出发对驻波能流密度进行分析才能弄清驻波瞬态能量转化和转移的机理.本文以一维机械横波形成的驻波为例，通过驻波中质元的位移、能量和能流密度的图像，再结合形变与弹性势能的关系，对驻波内部瞬态能量传播给出了直观分析，并分析了能流产生的机理，得到的结果有助于形象直观理解驻波内部能量传播.

1 驻波的波形 能量和能流密度

以横波为例，设角频率为ω，波幅为A的两列相干波，振动方向均沿y轴，沿x轴向相反方向传播，其方程为[1]

(1)

则驻波方程为

y=y1+y2=2Acosωtcoskx

(2)

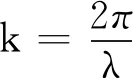
(3)

dEk=2ρA2ω2dVsin2ωtcos2kx

(4)

而质元的势能为[1]

(5)

其中G为弹性介质的切变模量(横波).由式(2)对x求偏微分得到

代入式(5)得到

dEp=2GdVk2A2sin2kxcos2ωt

(6)

弹性横波的波速

(7)

代入式(6)得到

dEp=2ρA2ω2dVcos2ωtsin2kx

(8)

由式(4)与式(8)得到质元的总能量

dE=dEk+dEp=

2ρA2ω2dV(sin2ωtcos2kx+cos2ωtsin2kx)

(9)

在水平向右的x轴上，由式(1)可得，右行波在dV质元中的能量[2]

dE1=ρdVA2ω2sin2(ωt-kx)

能量密度

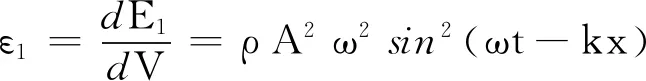
能流密度

I1=ε1v=ρvA2ω2sin2(ωt-kx)

(10)

左行波在dV质元中的能量

dE2=ρdVA2ω2sin2(ωt+kx)

能量密度

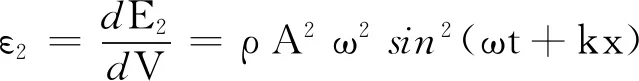
能流密度

I2=-ε2v=-ρvA2ω2sin2(ωt+kx)

(11)

上式中负号代表左行波能量传播方向沿x轴负向.则驻波的总能流密度

I=I1+I2=ρvA2ω2sin2(ωt-kx)-

ρvA2ω2sin2(ωt+kx)

得到

I=ρvA2ω2[sin2(ωt-kx)-sin2(ωt+kx)]=

-ρvA2ω2sin 2kxsin 2ωt

(12)

因为波动沿x轴传播，能量也只能沿x轴正向或者负向传播，如果根据式(12)计算出的I为正值，则代表波线上某处能量沿x轴正向传播，反之，如果I为负值，则代表该处能量沿x轴负向传播.

2 驻波的位移 能量和能流密度瞬态分布

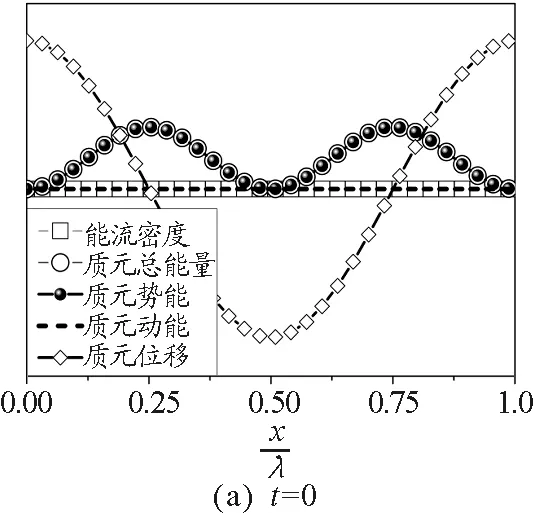
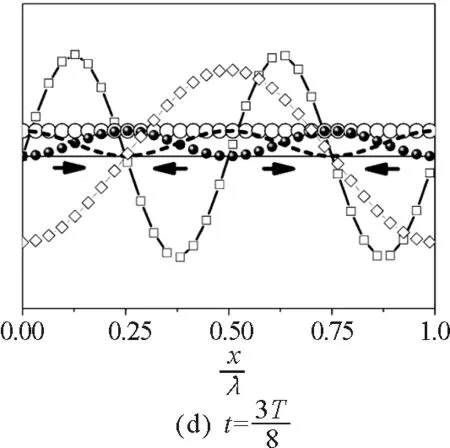
图时间内驻波的瞬态能流图

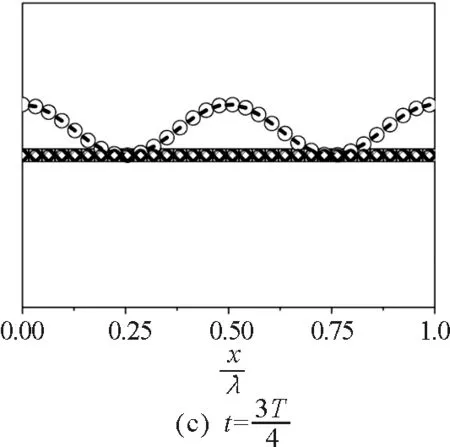
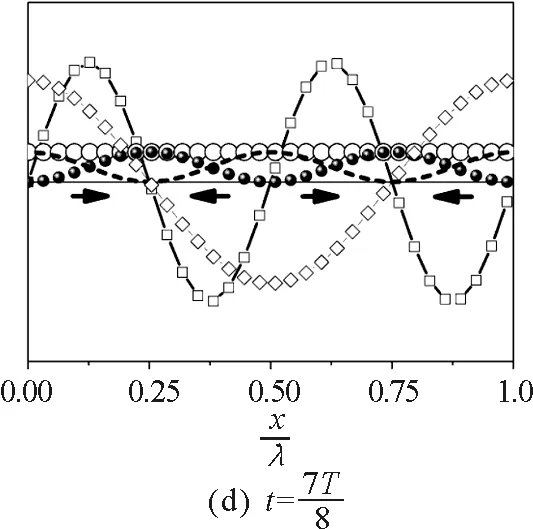
图时间内驻波的瞬态能流图

由图1(a)可见，在t=0时，驻波的波形为一余弦函数图形，波线上除了波节之外的所有质元均处于最大位置，运动速度为零，此时质元的所有能量全部为弹性势能.由图可见，波节处质元形变最大，而波腹处形变为零，因此波节处能量最大，而波腹处能量为零.同时可见此时波线上能流密度处处为零，因此t=0时波线上无能量传播.

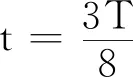
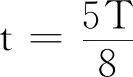
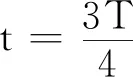
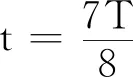
3 讨论

由图1和图2可见，在驻波振动过程中的任何时刻，波节处能流密度始终为零， 说明虽然驻波在振动过程中各段内部有能量传播，但从总体上看是分段独立振动的，各分段之间没有能量传播.

以弹性横波为例，在不考虑重力的情况下，除了所有质元均处于平衡位置的状态之外，如图1(c)和2(c)所示的状态，质元越靠近波腹形变越小，越靠近波节形变越大.当质元由最大位置向平衡位置振动时，某一质元受到相邻的离波节较近的一侧质元的切应力大于相邻的离波节较远的另一侧质元的切应力，切应力的合力指向平衡位置，做正功，将弹性势能转化为动能.而质元由平衡位置向最大位置运动时，受到的切应力的合力仍然指向平衡位置，做负功，将动能转化为弹性势能.因此弹性横波形成的驻波，能量的转化和转移要通过切应力做功来实现.

虽然驻波是分段振动的，每一段在振动过程中能量守恒，与独立谐振子有相似之处，但其中任意弹性质元的运动与独立谐振子有着本质区别.以波腹处质元为例，当其位移最大时，能量为零，处在平衡位置时能量最大，在振动过程中能量并不守恒.其他位置的质元也一样，在振动过程中部分时段吸收能量，总能量增加，部分时段释放能量，总能量减小.而独立的弹性谐振子，振动过程中总能量始终守恒.

对于波节处的质元，在振动过程中始终“不动”，其实只是质心不动.在振动过程中，波节处的质元要不断改变剪切形变大小来实现弹性势能的吸收和释放.

4 结论

(1) 一维弹性驻波，在相邻的两个波节之间存在着瞬态能量传播，能量部分时段从波腹传到波节，部分时段从波节到波腹.在传输过程中，相邻两波节之间总能量不变.

(3)当所有质元均处于平衡位置时，质元的能量全部为动能，此时波腹能量最大，波线上能流密度处处为零，局部没有能量定向传播.

(4)当所有质元均具有最大位移时，质元能量全部为弹性势能，此时波节处质元能量最大，波线上能流密度处处为零，局部亦无能量传播.