高超声速风洞来流扰动测量及数据后处理技术研究
余 涛, 王俊鹏, 刘向宏, 赵家权, 吴 杰,2,*
(1. 华中科技大学 航空航天学院, 武汉 430074; 2. 不伦瑞克工业大学 流体力学所, 德国 不伦瑞克 38108)
0 引 言
风洞实验是研究高超声速空气动力学的重要手段之一,因此高超声速风洞是研究高超声速空气动力学不可或缺的地面实验平台。常规高超声速风洞建成后,必须对流场的静态和动态品质进行鉴定。其中,动态流场品质,即自由来流扰动的模态特征,是衡量风洞设计成功与否的重要指标。对于常规低速风洞,衡量其动态品质的参数是湍流度,即速度偏差的均方根[1]。相对而言,高超声速风洞的流场结构复杂,其流场的动态品质定义更加困难。此外,诸多高超声速风洞实验发现:流场的动态品质对风洞实验测量结果有严重影响,如层/湍流边界层转捩[2-5]、激波/边界层干扰模式[6]、阻力系数测量[7]等,但是其中的作用机理仍不确定,有待于探索。尤其是高超声速流动下的边界层转捩问题,不同类型来流扰动子模态直接决定了转捩点位置及转捩波的类型,如涡波模态通常引起第一模态(Tollmien-Schlichting wave)转捩,而声波模态则导致第二模态(Mack wave)转捩[2, 8-10]。随着我国高超声速飞行器设计技术的迅速发展,研究人员对高超声速风洞实验的精度要求愈趋严格。因此,准确测量高超声速风洞中自由来流扰动子模态对基于高超声速风洞开展的相关基础科学问题的研究至关重要。
国外对高超声速风洞流场扰动的研究起步较早。1953年,Kovasznay使用热线仪对超声速来流扰动进行测量并建立了超声速流动的扰动模态理论[11-12]。其主要思想是将一阶小扰动引入到粘性、可压缩、带热传递效应的Navier-Stokes方程,将方程线性化后对应的解定义为超声速流动的扰动子模态,即涡波、熵波和声波模态。其中,涡波是速度场中的旋转分量的扰动;熵波则是在恒压下熵、密度和温度的变化;声波模态主要描述在熵守恒情况下压力、密度和温度的扰动量。在这3种模态中,涡波和熵波满足流线方程,因此可以通过流线追踪到扰动的产生源;相比之下,声波的产生机理更加复杂,且其可以跨越流线发展。此后,Morkovin对超声速自由来流中的扰动来源展开了更为深入的研究[13-14]。在Kovasznay对来流扰动分类的基础上,Morkovin进一步将声波模态细化为涡流马赫波和颤振马赫波(Eddy Mach wave and Shivering Mach wave)。前者主要由超声速湍流边界层所产生的以偶极子和四极子为主的声波辐射组成;后者则是由喷管上超声速湍流边界层的压力间断所引起的反射和衍射现象。此外,Morkovin和Laufer分别通过实验研究发现,在超声速风洞的自由来流中声波模态是主要扰动源[14-15]。普渡大学Schneider教授提供的一张图片形象地描述了高超声速风洞中自由来流的扰动模态类型及演化特征,见图1[16]。
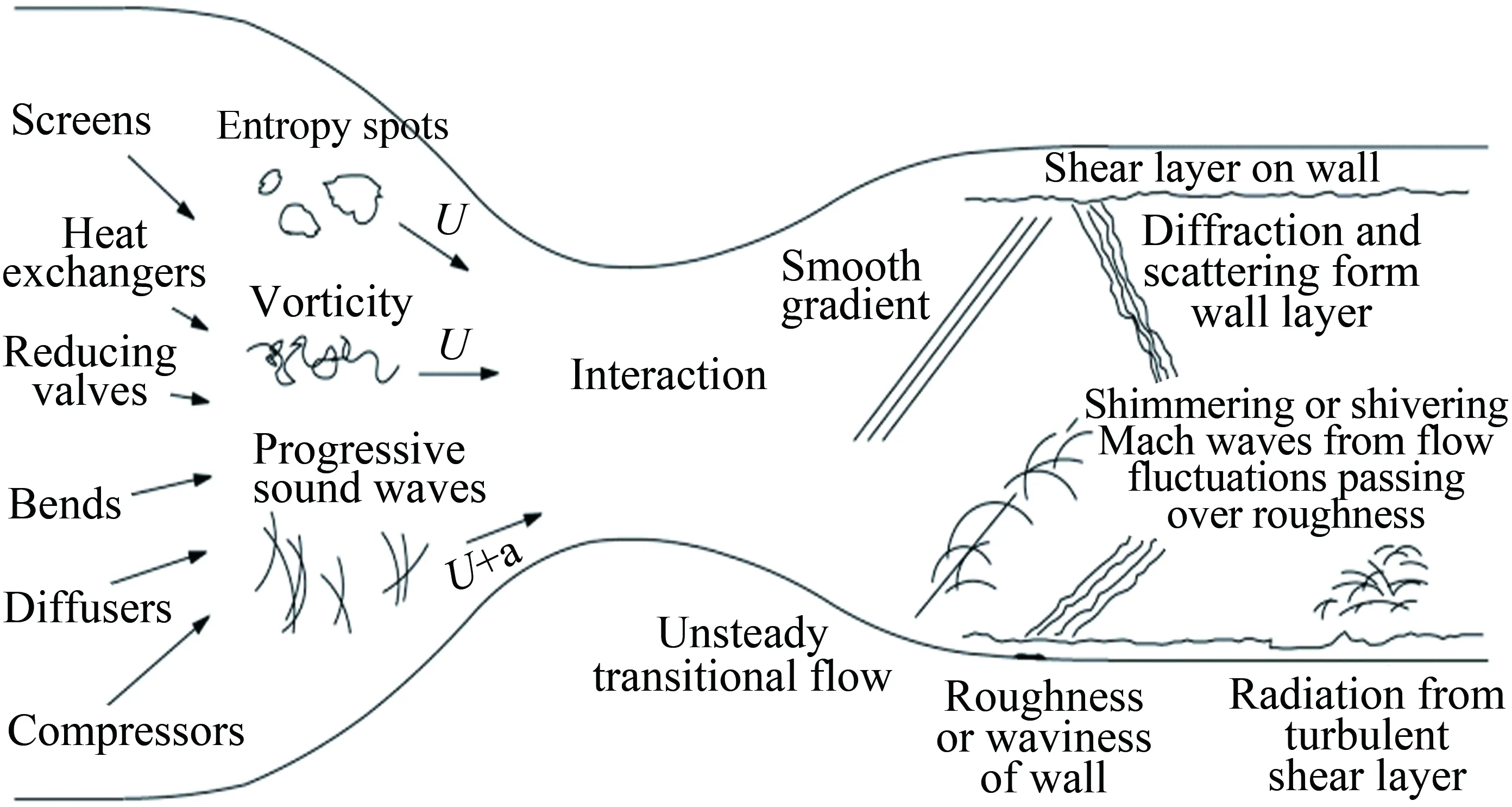
图1 高超声速风洞自由来流的扰动[16]
早期超声速及高超声速风洞的来流扰动测量以热线风速仪为主。由于热丝的直径小(本文所使用Dantec 55P11热丝直径为5 μm),在超声速及高超声速流场测量中通常可以近似认为热丝测量的流场脉动可以真实反映自由来流的脉动[17]。基于该假设,热线风速仪在超声速及高超声速流场测量中得到了广泛应用,如Smits使用热线风速仪对马赫数2.9的超声速流进行测量[18]、Wu等人对马赫数3的超声速边界层的均值和脉动剖面进行测量并与线化理论吻合[19]、Weiss等人对马赫数2.5的自由来流进行流场扰动校核[20]等。通过热线仪测量可得到流场的流量和总温脉动,以及两者的相关系数[11,18]。但是,流量和总温脉动并不是典型的非定常流动特征量,也不足以推导Kovasznay所定义的3种扰动子模态[21]。Laufer通过实验观察发现,在超声速风洞中喷管的湍流边界层所产生的声波模态通常为占优模态,并且通过热线测量发现流量和总温的扰动之间高度互相关[15, 20]。因此,Laufer假设来流扰动为单一噪声场,各流场参数之间满足等熵条件,进而可以推导其他流场参数的扰动特征。但是,Kovasznay认为在高超声速风洞自由来流中等熵假设不具备普适性,建议采用3种扰动子模态互不相关假设[11]。随着静风洞的出现[16,22],风洞来流扰动主要来源于上游的涡波与熵波,Laufer提倡的声波模态占优假设重新得到应用[23-25]。但是对于常规高超声速噪声风洞,分解来流扰动模态则需另辟蹊径。Logan等提出了一种新型的扰动模态分解法[26, 27],假设流场参数的脉动量(速度、温度和密度脉动)仅有两个不同的来源:声波模态
和其他模态,并认为声波模态与其他扰动模态不相关。该方法整体低估了声波模态对扰动模态的贡献。Masutti对冯卡门研究所的H3马赫数6风洞进行来流扰动模态标定,采用了双热线探头与Pitot管联合测量方法。在基于流场参数互不相关的假设下,发现声波模态并非主要扰动,尤其在高雷诺数下熵波甚至高于声波扰动模态的幅值[28]。Wu等人则通过单热线探头与Pitot管联合测量法,对德国不伦瑞克工业大学的马赫数3超声速风洞进行扰动模态测量,发现声波模态为来流的主要扰动模态,但是涡波与熵波模态也不可忽略[29-30]。之后,Schilden等人采用锥体探头-DNS联合法对德国不伦瑞克工业大学的马赫数6高超声速风洞进行了来流扰动模态的测量[31],在忽略涡波模态的前提下,结合实验测量与直接数值模拟方法,获得了来流中熵波与声波模态的幅值。与Wu[29]之前所使用的测量法得到的结果进行对比,发现声波模态在低频范围内吻合较好。Chaudhry 和 Candler采用DNS研究了自由来流扰动中声波扰动经过皮托探头产生的脱体激波后的传递函数[32],结果显示自由来流中的压力脉动经过脱体激波后脉动幅值反而增加,与Harvey以及Stainback[33]分别基于定常与非定常过程分析的结果有较大差距。
国内传统的高超声速风洞流场校测是将气流的速度场(马赫数分布的均匀度、梯度)和方向场(平均气流偏角)作为标准,而忽略了流场的动态特征,如压力、温度和密度脉动等,相关方面的理论研究较为缺乏。直到近年来,国内学者开展高超声速边界层转捩以及不稳定性研究,意识到来流扰动问题对边界层转捩波的重要性,方才重视风洞的来流扰动问题,如北京大学静风洞使用Kulite压力传感器测量皮托脉动压力[34]。虽然以上实验结果具有重大意义,但是仍未提供自由来流的扰动模态信息,如涡波和熵波扰动。
整体而言,目前高超声速风洞来流扰动的模态测量与后处理问题仍存在较大难度,国内外对于高超声速风洞来流扰动的标定尚无定论。在实际情况中,不同的风洞由于设计、加工方案的不同,流场的扰动子模态所扮演的角色也不同,加上部分测量仪器本身的激波干扰问题,更进一步将扰动模态分析问题复杂化。本文基于Kovasznay的扰动模态分解理论,讨论了不同类型高超声速风洞的来流扰动子模态分析方法,并以德国不伦瑞克工业大学马赫数6 Ludwieg式高超声速风洞的实验数据为例,展示了一种适用于常规高超声速风洞的来流扰动子模态分解技术。
1 实验设备、仪器及测量方法
1.1 马赫数6 Ludwieg管风洞
本文所研究的高超声速来流扰动模态测量与分析基于德国不伦瑞克工业大学串列式马赫数6高超声速风洞完成(实验部分由本文通信作者在德国不伦瑞克工业大学完成)。该高超声速风洞是一座Ludwieg式风洞,其实验段口径为500 mm,风洞的有效运行时间为80 ms。图2为马赫数6 Ludwieg式风洞示意图[35]。风洞的高压储气段与Laval喷管通过快速控制阀分开。在风洞启动前,储气段内储存着高温高压空气,而控制阀下游的部分则通过真空泵抽成真空。在开启快速控制阀门的瞬间,会产生一系列的非定常膨胀波,该膨胀波以声速向储气段的上游行进;与此同时,该膨胀波驱动管内的气体,达到对应的储气段启动马赫数(该马赫数取决于储气段与Laval喉道部分的面积比)。当膨胀波到达储气段底端后,再次被反射回来。反射膨胀波到达快速控制阀附近时,快速控制阀关闭,风洞的运行也同时结束。在快速控制阀的下游,受膨胀波驱动的高压气体会沿着Laval喷管膨胀加速,气流在到达实验段时加速到设计马赫数。更多关于该风洞的信息可参考文献[35-41]。
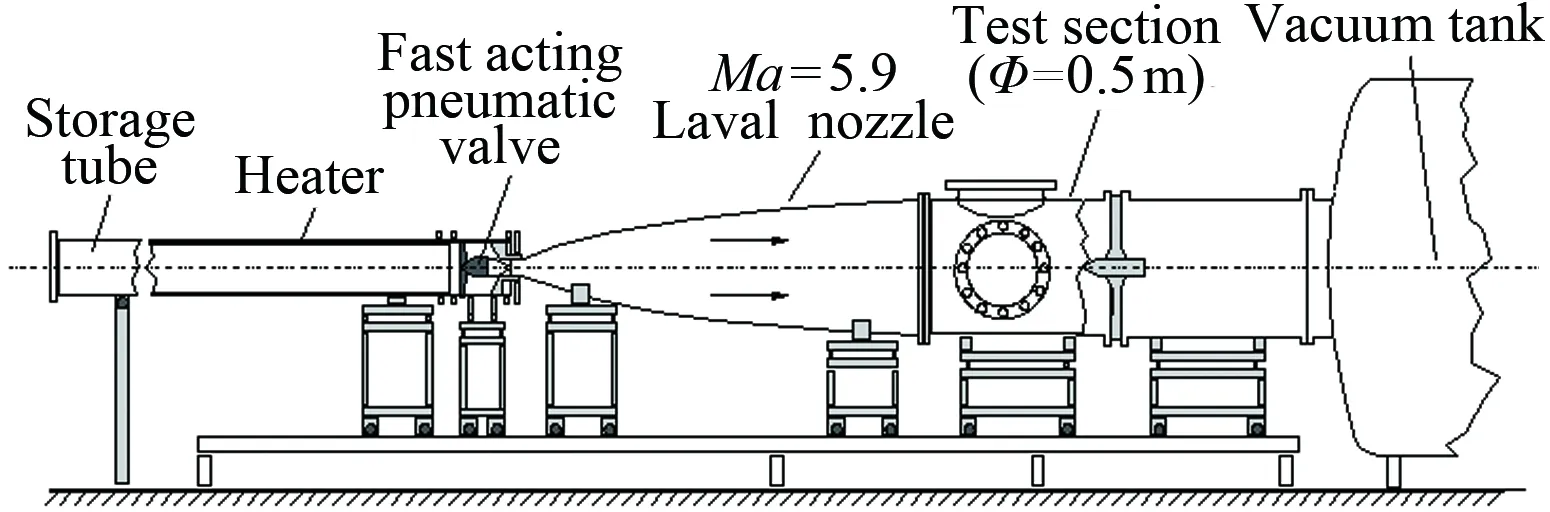
图2 德国不伦瑞克工业大学马赫数6 Ludwieg式高超声速风洞[35]
Fig.2Mach6LudwiegwindtunnelatTechnicalUniversityofBraunschweiginGermany[35]
1.2 实验测量仪器及数据处理方法
在高超声速风洞中,来流扰动脉动频率高、流动环境复杂,对来流扰动测量技术有较高要求。目前,广泛应用于高超声速风洞自由来流扰动测量的仪器主要是热线风速仪、皮托探头以及聚焦激光差分干涉仪。其中,热线风速仪可以获取来流的总温和流量脉动,其动态响应频率可达百千赫兹以上;压力皮托管测量的是激波后总压脉动,虽然动态响应频率更高,但是其所测得的信号并非自由来流中的真实压力脉动;聚焦激光差分干涉仪采用的是非介入式测量方式,可以测量自由来流中的密度脉动。本文使用了恒温热线风速仪(Constant Temperature Anemometer, CTA)和皮托管,见图3和4,结合两种不同仪器的测量数据,通过扰动模态分析,获取不同扰动子模态的特征。
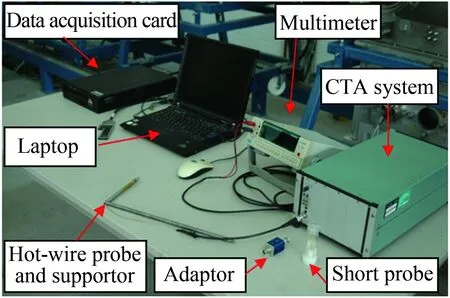
图3 热线风速仪系统

图4 皮托压力探头
热线仪的测量原理是热丝产生的热量与周围气流对流换热平衡。对于超声速及高超声速流动,目前广泛采用以下经验公式描述该过程:

(1)
其中,Nu为Nusselt数,I为通过热丝的电流,R为热丝的电阻,k为热丝周围流体热传递系数,L为热丝长度,T为温度,η是总温恢复系数。下角标w表示热丝的状态,0则表示驻点流动状态。对于热丝而言,X和Y通常为常数,其主要取决于热丝本身的特性。f(τ)和g(τ)分别是过热比τ的函数;n为雷诺数指数,通常在0.40~0.55之间。根据经验,当来流马赫数大于1.3时,Nu与马赫数无关;此外,当热丝雷诺数大于20时,总温恢复系数η为常数(0.94±0.001)[42]。由于热线仪的电压输出是流量ρu和总温T0的函数,可表达为:
E=E(ρu,T0)
(2)
对式(2)进行如下转换:
E′=km(ρu)′+kT0(T0)′
(3)
其中,
(4)
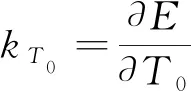
(5)
km为流量敏感系数,kT0为总温敏感系数,这两个重要的参数都是热丝过热比的函数,需要通过校核进行标定。在实际数据的分析过程中,需要对式(3)进行变换,通常的做法是将式(3)进行平方后整理为均方根值的形式:

(6)
在使用热线仪进行测量前,通常需要对热线仪进行校核,确定热线的敏感系数。在低速流动中,通常将流动视为不可压缩流动,且对环境温度的考虑不多。对于超声速及高超声速自由来流而言,可压缩性与温度的影响不可忽略。为了校核方便,通常将式(1)表达为以下形式:
E2=F+M(ρu)n
(7)
其中,F和M是过热比和总温的函数。对式(2)进行变化得到:

(8)
其中,Ra是热丝在环境温度下的电阻。对于式(7)和(8),可以将过热比函数F和M与热线仪参数以及周围流场参数联系起来:
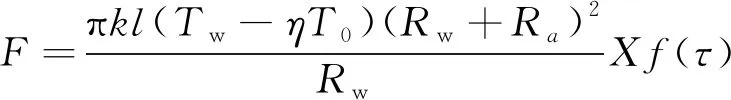
(9)

(10)
在式(9)和(10)中,D为热丝的直径,μ为流体的动力粘性系数。进一步可以将热线仪的流量敏感系数和总温敏感系数进行如下表达:

(11)
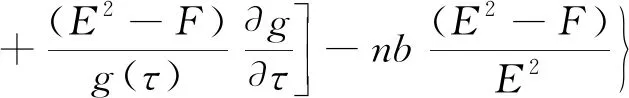
(12)
其中,a、b为常数,n为式(1)中的雷诺指数。认为热丝周围的流体热传递系数以及动力粘性系数满足如下关系式:
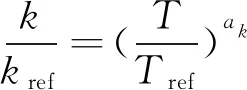
(13)
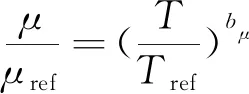
(14)
其中,下角标ref表示参考值,对于理想气体,ak=bμ=0.768[11]。为了获取热线仪的流量和总温敏感系数,通常的做法是在某一特定总温下,改变来流的雷诺数,对流量的敏感系数进行校核;对于温度的敏感系数,则需要在特定流量下通过改变来流的总温来获取。对于常规超声速及高超声速风洞,改变来流的总温后,往往涉及到流量的变化。因此,本文选择了Smits发展的方法[18],即保持风洞的总温不变,在不同的过热比状态下改变风洞自由来流的单位雷诺数,建立起热线风速仪输出电压与流场自由来流流量的关系式,如图5所示。基于图5中的校核曲线,可以同时获取f(τ)和g(τ)的函数分布。在确定了f(τ)和g(τ)的函数分布后,根据式(11)和(12)可最终获取流量和总温敏感系数的分布,如图6所示。由图6可知,在低过热比条件下,热线仪对总温变化更为敏感;随着过热比的增加,热线仪对流量变化更为敏感。

图5 热线仪校核曲线
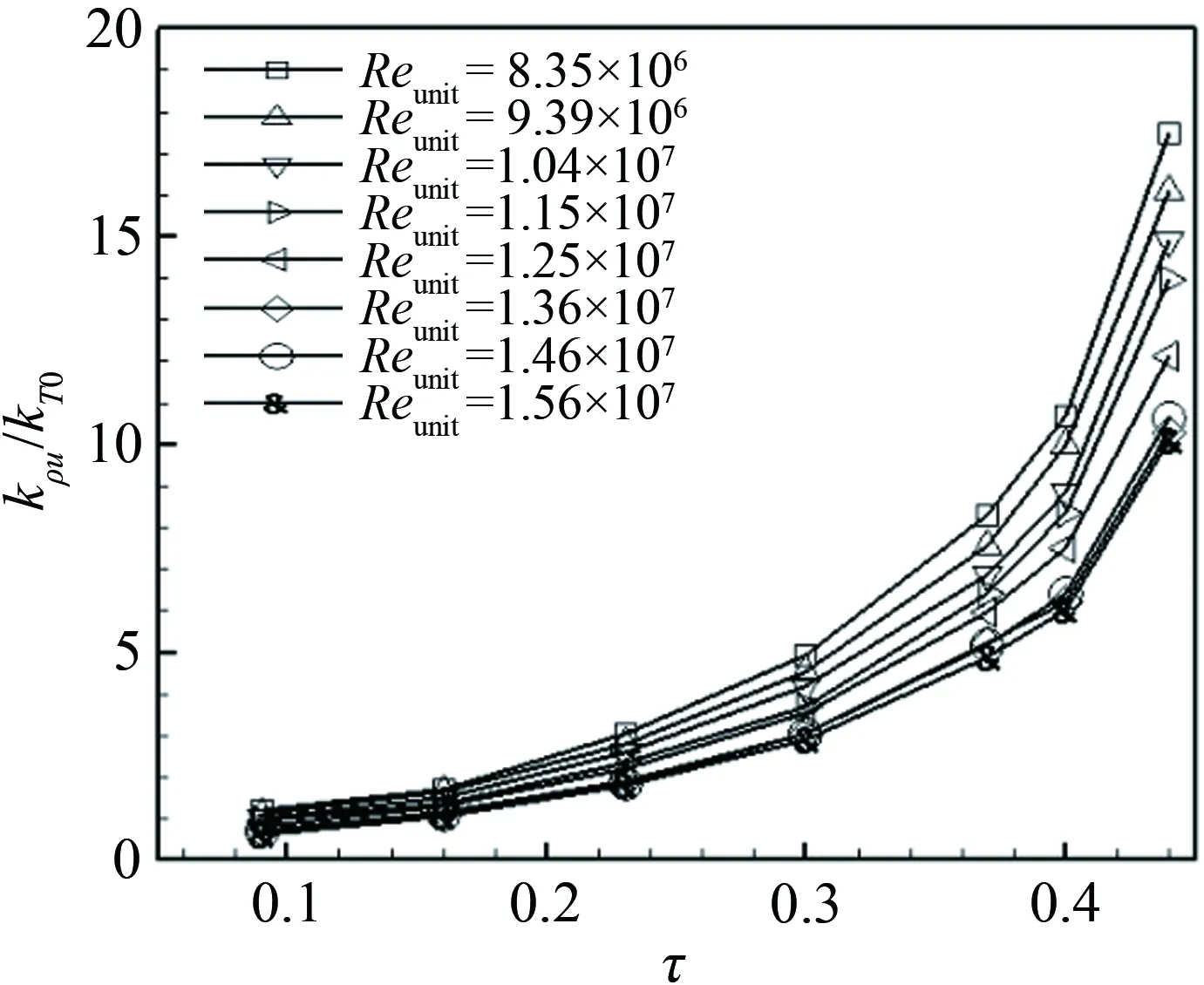
图6 热线仪流量与总温敏感系数比较
皮托探头测量激波后的总压脉动,为了与热线测量的数据进行耦合,需要将总压脉动转化为自由来流的静压脉动。由于不同的扰动子模态经过激波后均产生新的声波脉动,即使通过直接数值模拟,也只能对极为简化的情况进行分析。在本实验中,采用Chaudhry等人最近直接数值模拟所获得的传递函数[32]。
2 高超声速来流扰动模态及其分解方法
通过热线风速仪与皮托探头测量,可获取流量、总温以及压力脉动的信息,但是以上信息并未与扰动子模态进行关联。为了定量标定扰动子模态,需要进行扰动模态离解分析。
Kovasznay在1950年首先发展了使用热线仪测量超声速来流中扰动子模态的技术,并且基于小扰动理论发展了扰动模态理论,对超声速流动中的小扰动进行定性与定量的描述[11-12]。根据不同流场参数的特征,Kovasznay认为超声速流场中的扰动是3种扰动子模态的叠加,即涡波ω、熵波θ和声波σ扰动,各子模态扰动的定义如下所示:
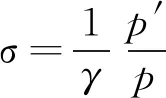
(15)

(16)

(17)
上角标′表示流场参数的脉动,γ为比热比,Ma为来流马赫数,u、T、p分别为速度、温度和压力,nx为声波的方向余弦。通过以上定义可见,来流扰动模态通常由多个流场参数以及它们之间的相关系数决定。首先,根据本实验测量仪器所能获取的流场参数的定义,可得:
m=ρu
(18)

(19)
p=ρRT
(20)
T为静温,cp为定压比热容。由于已经假设自由来流方向与热线放置方向垂直,可认为除了流向以外,其他方向的速度脉动为零。对式(18)~(20)进行变化可得:
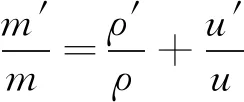
(21)

(22)

(23)
其中,

(24)
β=α(γ-1)Ma2
(25)
将式(21)~(23)左右变量进行更换后,代入到式(15)~(17),即可得到扰动子模态与实验测量参数之间的关系式:

(26)
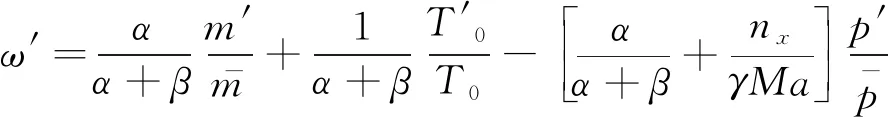
(27)
(28)
根据式(26)~(28)可知,在小扰动假设条件下,联合热线风速仪和皮托探头测量,可最终获得自由来流的扰动子模态幅值。
3 实验数据与分析
3.1 皮托管测量
本文皮托压力测量过程中采用的是Kulite XCQ 系列压力传感器,其有效频率最高达40 kHz。实验中最低来流单位雷诺数Reunit为8.35×106/m,最大为15.6×106/m。图7为马赫数6自由来流中不同单位雷诺数下的皮托压力脉动分布,实验结果显示在低雷诺数下皮托压力ppitot脉动幅值约为1.8%。整体而言,该风洞的流场质量较冯卡门研究所马赫数6风洞和普渡大学马赫数6风洞的噪声状态低[28,35]。此外,随着单位雷诺数的增加,皮托压力脉动幅值下降,说明该高超声速风洞属于典型噪声风洞[43],其噪声主要来源为Laval喷管表面湍流边界层所产生的噪声辐射。
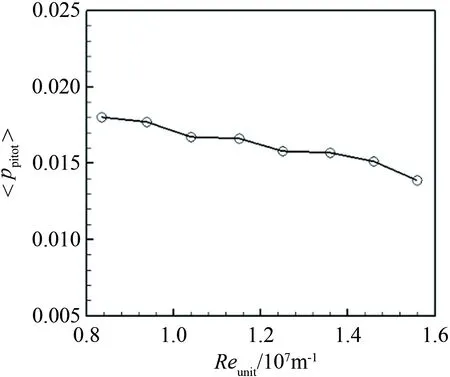
图7 自由来流中皮托管压力脉动
但是,皮托管测量的是激波后的总压脉动,不能直接视为自由来流的压力脉动,我们这里使用Chaudhry等直接数值模拟所获得的传递函数[32]。 Chaudhry等使用直接数值模拟对具有迎角的声波扰动穿越激波过程进行分析,探明了自由来流中压力脉动穿越激波的变化特征,并建立了来流扰动与激波后总压脉动之间的关系(图8),可见皮托探头所产生的激波前后压力脉动比值同时也是频率的函数。 由于本文使用的压力传感器的动态响应仅达到40 kHz,图8显示在40 kHz以下,激波前后压力脉动的比值约为0.38~0.4(之后所使用的热线仪数据也仅仅使用45 kHz以下信号)。根据以上关系,可以估算皮托总压脉动与自由来流静压脉动的均方根比值为0.632。
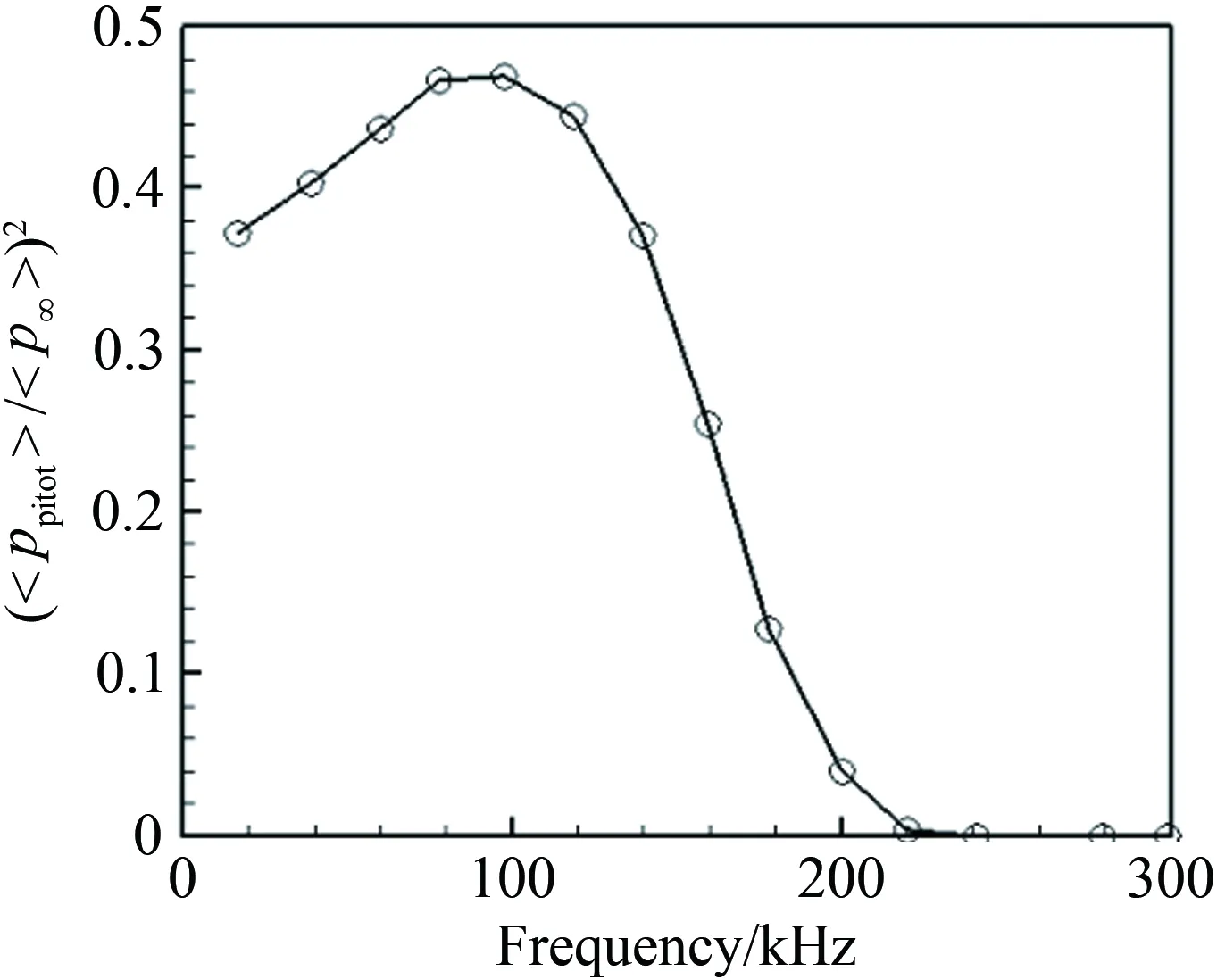
图8 皮托总压与马赫数6自由来流压力脉动传递函数(声波迎角为120°)[44]
Fig.8TransferfunctionbetweenpitottotalpressureandMach6freestreampressuredisturbance(sonicattackangleis120°)[44]
3.2 热线测量
为了确保实验数据具有统计意义,热线仪的测量过程中热丝探头的位置与皮托探头的位置保持一致,风洞运行的雷诺数也保持相同。受限于热丝的最大温度,实验过程中使用的最大过热比仅达到0.55。通过热丝校核,得到流量和总温脉动的均方根值,如图9所示。流量的脉动随着来流雷诺数的增加而逐渐降低,与皮托总压脉动的趋势相似;但是,总温的脉动在低雷诺数下跳跃较大,且随着雷诺数增加,其幅值也增加。
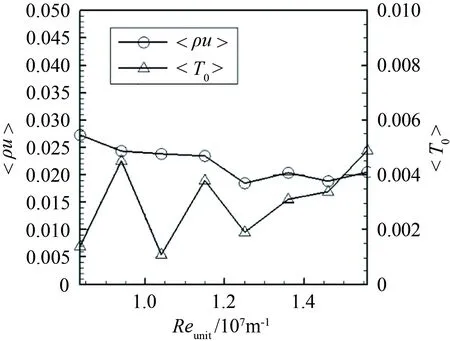
图9 马赫数6自由来流流量和总温脉动
根据第2节扰动模态分解的方法,进行各扰动子模态的计算,获得图10所示结果。声波扰动模态远高于涡波和熵波扰动,占据了总扰动的60%以上;相比之下,熵波和涡波扰动较低,约各占总体扰动量的15%。由于该Ludwieg式管风洞流场结构极为简单,没有复杂的阀门机构,涡波扰动基本可以忽略;至于熵波扰动,本次实验过程中仅仅加热至430 K,且严格控制风洞运行间歇的稳流时间,故其幅值预期也较低。
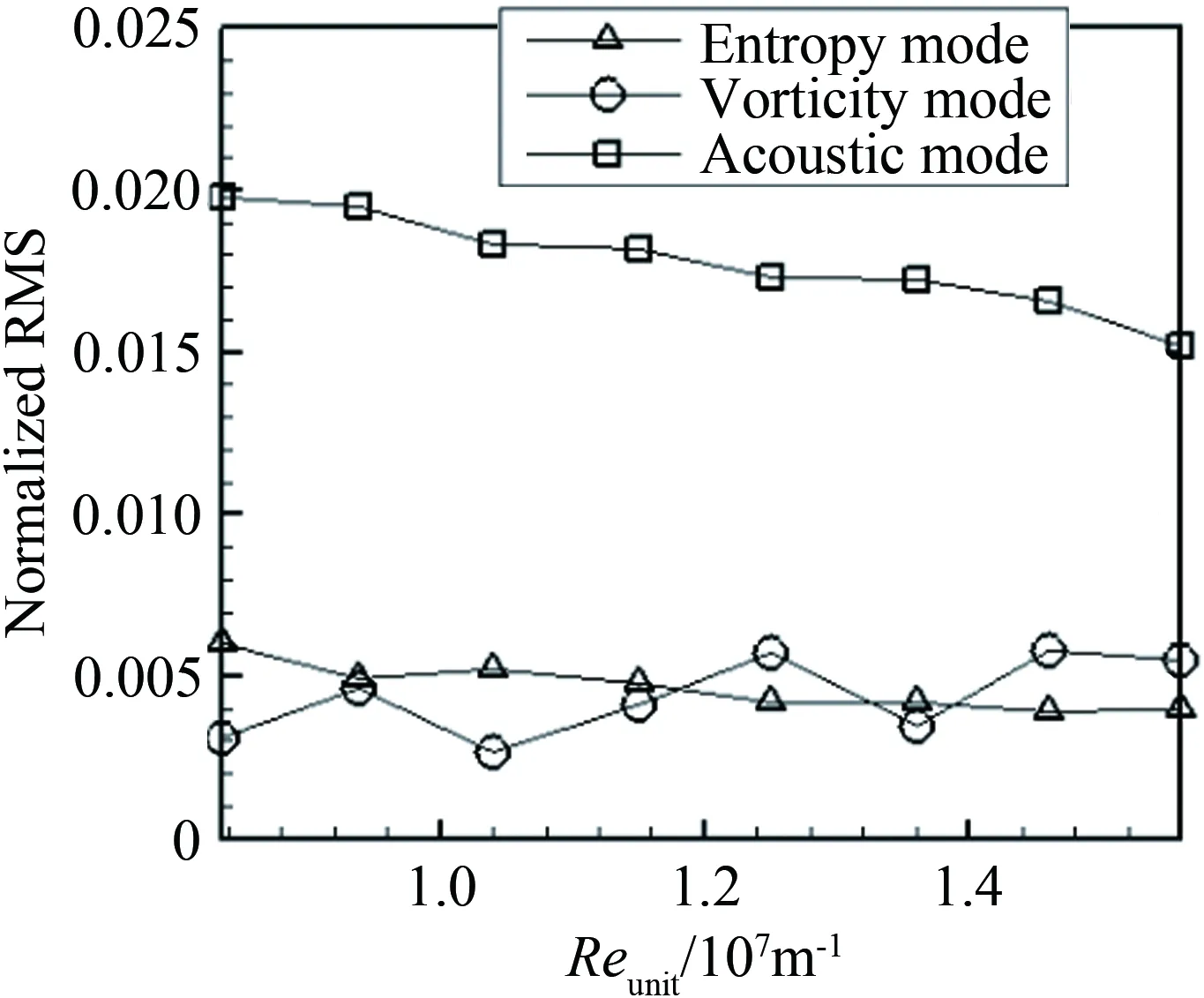
图10 自由来流扰动子模态分析
此外,为了进一步证实该风洞属于噪声为主要扰动的风洞,对热线输出电压信号与敏感系数之间的关系进行了线性拟合,如图11所示。拟合结果显示,获得的热线电压输出与热丝敏感系数存在良好的线性吻合,且随着来流雷诺数的增加,拟合直线的斜率减小,与Laufer判定声波占优脉动风洞的特征一致[15]。由于声波占优假设不是本文的重点,这里不再阐述,更多细节可参考文献[15]。
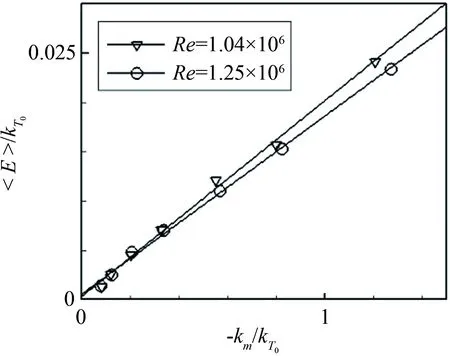
图11 热线仪输出电压与敏感系数线性拟合
Fig.11Linearfittingofoutputvoltageandsensitivitycoefficientofhot-wire
4 总结与讨论
本文基于德国不伦瑞克工业大学马赫数6 Ludwieg式高超声速风洞的自由来流试验数据,介绍了高超声速风洞中自由来流扰动模态的测量与分析问题,通过联合使用热线风速仪和皮托压力探头测量技术,并结合直接数值模拟结果,进行来流扰动模态的离解分析,最终获取了高超声速流动下不同扰动子模态的幅值。实验结果显示,该风洞为典型的噪声风洞,其声波模态高达扰动总模态的69%,熵波和涡波模态各约占15%。该实验技术为国内诸多高超声速风洞的流场扰动测量提供了思路,为基于高超声速风洞开展的实验提供了借鉴与参考。
但是,本文在后处理方法上假设流场脉动量之间互不相关,在小扰动假设前提下成立,有一定的局限性。此外,该实验数据后处理方法与Ali[45]及Wu等[29,39]所使用的方法不同,且在子模态扰动幅值上呈现较大差距,其原因还需要进一步探究与验证。本实验研究还明确了自由来流压力脉动在扰动模态计算过程中的重要性。
传统的通过皮托探头数据推导来流静压的方法,如Harvey及Stainback[33]分别基于定常与非定常过程的转换,均与目前直接数值模拟的结果呈现极大差距,甚至是相反的趋势,直接影响了扰动子模态的幅值。因此建议未来采用非介入式的光学测量方法对该问题进行深究。
最后,由于本文所使用测量方法与常规单一测量方法(如PIV或者热丝测量)不同,使用两种不同的测量技术在不同车次的风洞中测量所引入的误差也更大,如何定量确定本方法的误差范围也将是接下来的研究重点。

