基于最短路径算法的农产品配送路径优化研究
杨君子 张利民


[摘 要]最短路径算法不仅具有重要的理论意义,而且具有重要的实用价值,它应用于交通运输、设备更新、线路设计等各方面。本文介绍了Dijkstra算法,并针对衡水市某区域蔬菜农产品配送到小区超市要求路线最短问题,建立数学模型给出最佳方案。
[关键词]最短路径;Dijkstra算法;农产品
[中图分类号]F326.6 [文献标识码]A
最短路问题是图论中非常重要的最优化问题之一,它是一个在现实生活中经常被用到的基本工具,它可以解决现实生活中的许多实际问题,如城市中的管道铺设、交通运输、电子导航、线路安排、工厂布局、设备更新等。另外,它还可以解决最快路径问题、最低费用问题、邮政选址问题等其他最优化问题。最短路问题,一般来说就是从给定的网络图中找出任意两点之间距离最短的一条路,就是从图G中某对顶点vi和vj(i≠j)之间的所有路径中权值之和最短的一条路径作为顶点vi到頂点vj的最短路径。
1 Dijkstra算法
Dijkstra算法是在一个赋权有向图中能够寻找出最短路问题的最好方法,它是由荷兰计算机科学家E.W.Dijkstra在1959年提出来的,它适用于所有弧的权值为非负的情况(即wij≥0)。Dijkstra算法在图论中是一种典型的单源最短路径算法,可以用来计算从一个给定的节点vs到其他所有点中任意一个点vj的最短路。Dijkstra算法的基本思想:从指定的点vs出发,逐渐一层一层向外扩充去寻找最短路。
2 农产品配送最短路径问题
由于农产品中生鲜、鲜奶等时效性强,利用最短路径算法解决配送的路线问题,以衡水市在某一个区域的农产品运输路线为研究背景,我们将对运输流程做进一步的研究,首先将实际生活中复杂的地理线路简单化,然后将利用最短路径的逐次逼近法来优化出最佳配送路线,使送货员到达每个小区超市的路径最短。
路线的选择是衡水市桃城区的一个区域,在将现实问题平面化、虚拟化的过程中还应注意一些具体相关细节问题,考虑到现实与模型的差别和计算的方便以及一些其它因素,在此对现实情况的模型化做了如下的调整:①每条街道都想象成为直线,忽略现实两个地点之间的道路是曲折的这一客观因素;②一些胡同和小的路段忽略不计,只是标记出醒目的街道和路;③不考虑路线的车流量以及拥堵问题,通过每条路的各个条件都相同;④在运输的过程中不考虑经过某个具体路段的时间要求,单纯地考虑怎么样规划路程,使得送货员在最后送到每个小区超市,所走的路线最短。
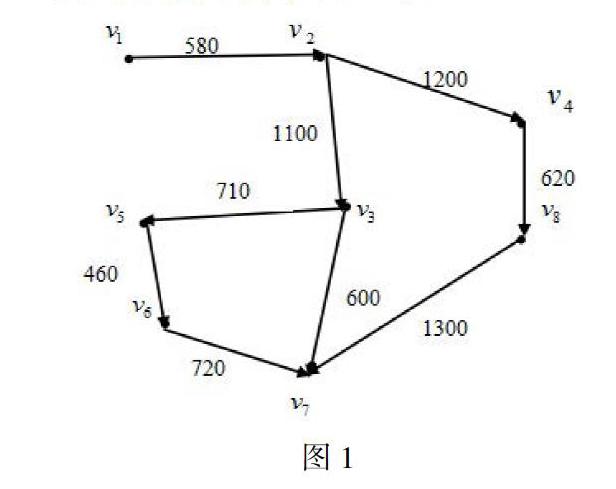
将现实道路虚拟化、模型化的过程:我们将日常生活中的实际问题转化到我们的理论实践当中,从图论的角度考虑,为了使送货员到达每个小区超市路程最短,将实际图转化为网络图,如下图(两个区域之间的距离单位为:m):
v1代表鑫城嘉苑,v2代表恒丰理想城,v3代表桃城苑,v4代表华世鑫城,v5代表万和苑,v6代表中央名邸,v7代表广厦上城,v8代表中和盛景
在图1的网络图中,各个节点代表各个小区的名称,每条边上的权值可以体现出能够直接连通区域之间的距离。求出图1所示的赋权有向图D中从v1到各点的最短距离。设从任意一点vi到任意一点vj都有一条弧,如果没有,则添加一条弧(vi, vj),并令wi=+∞,记Pj = P(vi, vj)为从v1到点vj的最短路长。
初始状态:
第一次迭代:
同理可得:
第二次迭代:
(下转页)
(上接页)
第三次迭代:
第四次迭代:
算法终止。由上面的推导过程可以得到送货员到达每个小区超市的最短路径为:。
在日常生活中,不管是路程最短还是时间最短、费用最短以及各种情况的选址问题等都可以应用最短路径算法来解决。新的最短路径算法的不断出现与经典的图论、发展更加完善的计算机数据结构以及算法的有效结合都是密不可分的。最短路径问题仍是计算机科学、运筹学、交通工程学、地理信息学等学科的一个研究热点。
[参考文献]
[1] 胡运权.运筹学教程[M].清华大学出版社,2012.
[2] 周维,杨鹏飞.运筹学[M].科学出版社,2008.
[3] 杨丽娟,刘渤海.基于Dijkstra拓展算法路线优化[J].长春工业大学学报,2015(01).
[4] 胡运权.运筹学基础及应用[M].高等教育出版社,2004(04).

