Optimal estimation of the amplitude of signal with known frequency in the presence of thermal noise*

Jie Luo(罗杰),Jun Ke(柯俊),Yi-Chuan Liu(柳一川),Xiang-Li Zhang(张祥莉),Wei-Ming Yin(殷蔚明),and Cheng-Gang Shao(邵成刚)

1School of Mechanical Engineering and Electronic Information,China University of Geosciences,Wuhan 430074,China

2MOE Key Laboratory of Fundamental Physical Quantities Measurement,School of Physics,Huazhong University of Science and Technology(HUST),Wuhan 430074,China

Keywords:optimal amplitude estimation,thermal noise,torsion pendulum,measurement time

1.Introduction

The torsion pendulum is an extremely sensitive physical measurement device of detecting weak forces,which has been used in many gravitational experiments,[1]such as tests of Newtonian gravitational inverse square law,[2,3]tests of weak equivalence principal,[4]tests of Lorentz invariance,[5]etc.The most significant character in these experiments is that the frequency of the signal to be detected is known accurately.[6]Therefore,the accurate estimation of the amplitude of signal with known frequency is a crucial step in obtaining the final experimental result.

The variance of estimating the amplitude can be contributed by a variety of noise sources,such as thermal noise,local gravitational gradients disturbances,microseismic noise,and so on,[7]among which the thermal noise sets the most fundamental limit to the estimation of the amplitude of the signal with the highest precision.[8]Thermal noise originates from the Brownian motion,[9,10]where the limit of it with torsion pendulum has been long known and extensively studied.[7,11,12]Braginsky and Manukin discussed the situation when the period of the applied torque is equal to the natural period of the pendulum.[12]Chen and Cook discussed the situation when the applied torque is constant in time.[7]According to fluctuation–dissipation theorem or Nyquist theorem,[13–15]the least detectable torque in the presence of the thermal noise can be written as

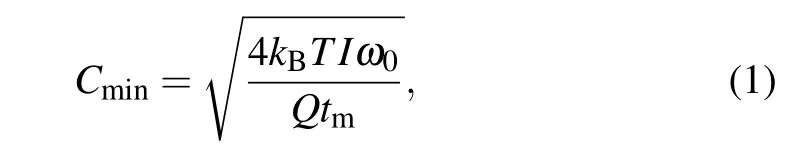
where kBis Boltzmann’s constant,T is the absolute temperature,I is the moment of inertia of the pendulum,ω0is the free resonance frequency,Q is the quality factor,and tmis the measurement time.The formula can be regarded as the minimum variance of estimating the amplitude of a periodic torque due to thermal noise.However,the result is only theoretical and we have to linke the thermal noise limit with the data processing method on amplitude estimation.[14]There are many methods to estimate the amplitude of signal with known frequency,such as the fast Fourier transform method,the nonlinear leastsquare fitting method,and the correlation method.[16–18]

Different methods can estimate the amplitude with different accuracies.[14]We have proved that the correlation method and the nonlinear least-square fitting method are better than others,which have been widely used in subtle signal analysis.[6,14]It has to be mentioned that the correlation method is equivalent to the nonlinear least-square fitting method for amplitude estimation.[2,3,14]By using the correlation method,we found that the variance can meet the limit of Eq.(1)only when the measurement time is much longer than the relaxation time of the torsion pendulum. However it is difficult to achieve for a high-Q torsion pendulum and the system would not be stable over the long times of observation.[7]In pursuit of higher precision and the convenience of experimental observation,the variance of estimation method must be improved when the measurement time is limited.

In this paper,an optimal estimation method to determine the amplitude of the signal with known frequency in the presence of thermal noise is proposed.Considering that the thermal driving torque is white noise,we first derived the optimal estimation formula for white noise by using the maximum likelihood estimation. To obtain the optimal formula for thermal noise,we use the equation-of-motion filter operator to transform the observable to the torque basis.Then,a transformation back into the displacement representation can give the result.[19]In the gravitational experiments conducted by Huazhong University of Science and Technology(HUST)group,the measurements are often made at levels near or below the thermal noise floor of instruments.[20–22]We finally apply the optimal estimation method to process a typical experimental data set of obtaining the amplitude of the gravitational calibration signal of testing the Newtonian gravitational inverse square law(ISL).The results are in agreement with of our model and prove that the new method is superior even for a real physical system,which is instructive and significant to the experimental design with torsion pendulum.

2.The least detectable torque

Considering the case where a mass with moment of inertia I is suspended in the Earth’s gravitational field by a fiber.The angular fluctuations,subject to the velocity damping.[14]Furthermore,there is a sinusoidal torque acting on the pendulum.Then the equation of motion of the pendulum can be expressed as

where b is the damping coefficient,k is the torsional constant of the fiber,Tth(t)is the thermal fluctuation torque,and Ts(t)is the applied torque on the torsion pendulum. According to fluctuation–dissipation theorem,[15]the thermal fluctuation torque has zero expectationand the autocovariance operator is[14]

where the mean value denoted byis an ensemble mean.The mean-square spectral density of the fluctuation is,therefore,[14]

According to the Wiener–Khinchin theorem and contour integration methods,the autocorrelation function Rθ(τ)will be[23]

where ω1is the resonance frequency,which is defined by=and τ=t1−t2represents the lag time.The applied torque is assumed to be Ts(t)=Ccos(ωst+ϕs).In actual experiment,ϕscan be zero by selecting the suitable initial phase.The applied torque can be rewritten as Ts(t)=Ccosωst.In experiment,two timescales are particularly discussed:and.The first represents the situation when the system reaches the equilibrium.The second represents the commonest situation for the pendulum.[7]

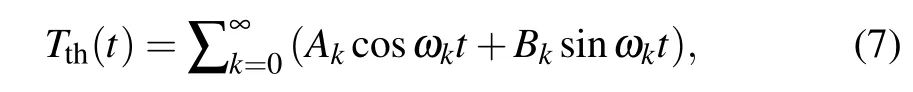
where ωk=2πk/tm,Ak,Bkcan be determined by

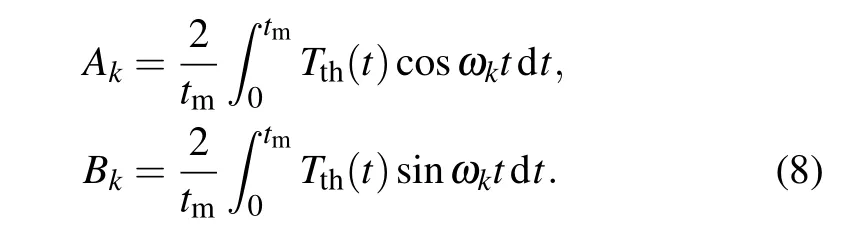
We adopt the same criterion used by Braginsky for a signal to be detectable in any observation at time t:[12]Substituting Eq.(3)into Eq.(8),we can obtain

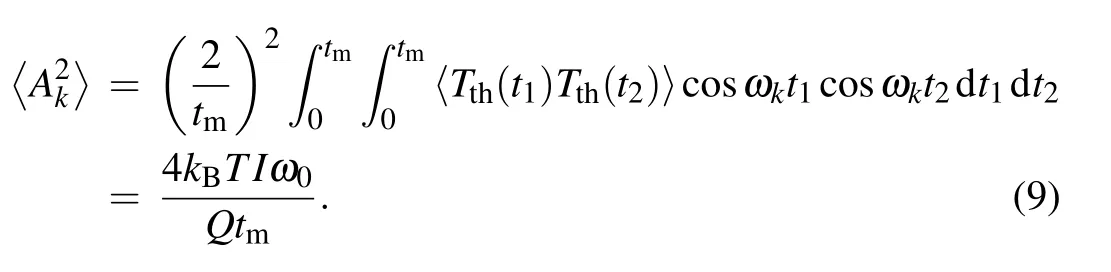
Comparing Eq.(9)with Ts(t)at the same frequency and same phase,the least detectable torque can be determined as

It can be seen that the difference between the free resonance frequency of the torsion pendulum and the frequency of the applied torque is an important factor for determining the least detectable torque.By satisfying the following equation:the first term in Eq.(11)can be distinguish from the second term in the frequency domain.So equation(10)also can be used in this situation.The result proves that equation(10)is valid in any circumstances for placing the signal frequency different from ω1.According to Eqs.(6)and(11),the least detectable amplitude of the displacement of the pendulum to the applied torque can be obtained as

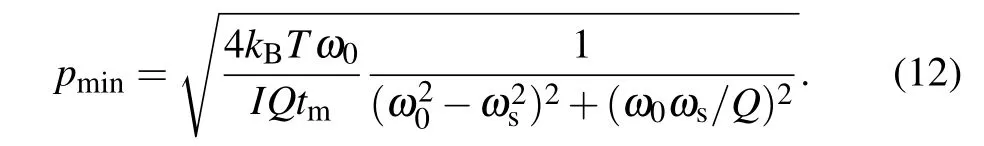
The formula also can be regarded as the minimum variance of estimating the amplitude of a periodic displacement due to thermal noise.

3.The correlation method

Here,we will calculate the variance of amplitude estimation due to thermal noise with the correlation method.However,there are something we must consider firstly. For the experimental data,the free torsional oscillation is an important component of the pendulum’s twist. The free torsional oscillation can be written as:

which has the same resonance frequency as the second term in Eq.(11).Because the target of the experiment is to obtain the amplitude of the sinusoidal signal with known frequency ωs,we applied a digital filter to remove the sinusoidal signal of the resonance frequency before proceeding with the analysis.The selection of the digital filter will be discussed in Section 5.In this case,the filtered data sequence becomes

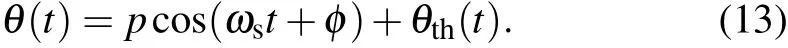
Now,we can extract the amplitude p by correlation method.Put bs=pcosφ,as=psinφ,tm=mTs,the estimation can be expressed as

Based on thermal noise model,we can obtain the variance according the following equations

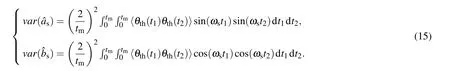
Substituting Eq.(3)into Eq.(15),we have

where

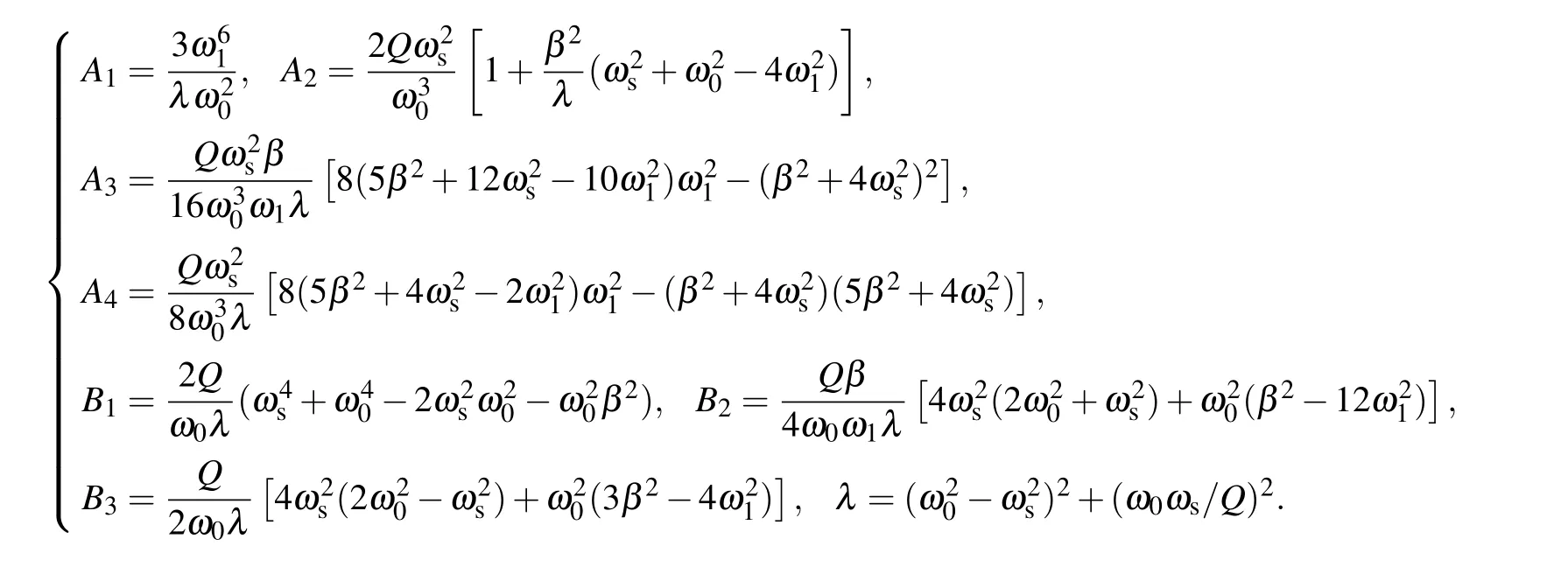
For telling the difference between the square of Eq.(16)and Eq.(12),we select the typical experimental parameter of HUST.In this case,Tsis set to 400 s,I ≈6.97×10−5kg·m2,T0≈586 s,the quality factor Q is about 2268,kBis 1.38×10−23J/K,and the absolute temperature T is 300 K.The relaxation time of the torsion pendulum can be calculated τ*=2/β=4×105s.Figure 1 shows the variance of the correlation method as a function of the measurement time.We state the measurement time in unit of signal periods,Note that this variance does not decrease monotonically with increasing measurement time tm.It is apparent that the correlation method is not the optimal method because the line(cycle)is not completely consistent with the line(square),especially when the number of signal periods m<104(tm=4×106s).The gap between the correlation method and thermal limit is caused by the difference in statistical characters of thermal noise and white noise for the torsion pendulum.This is what we expect to fill with by using an optimal method with a short time interval.

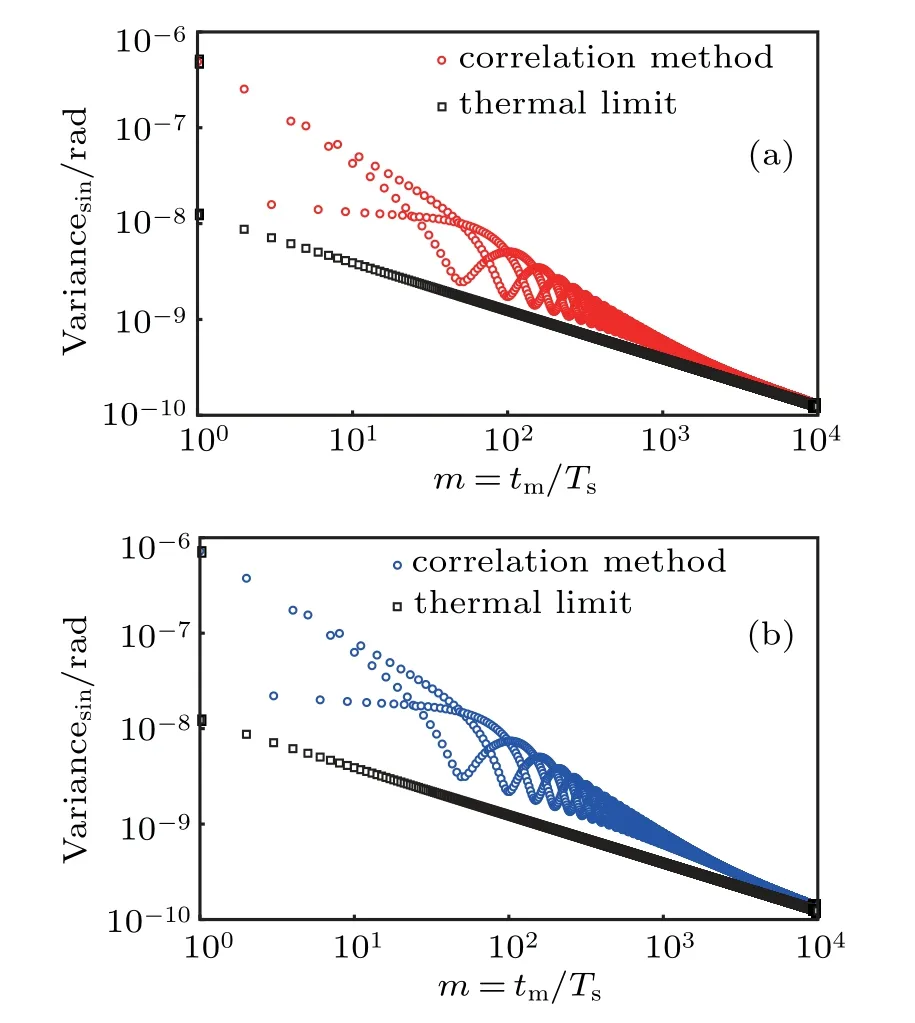
Fig.1.The variance of amplitude estimation with the correlation method as a function of m:(a)the variance of estimating the cosine component,(b)the variance of estimating the sine component.The line(circle)is fitting to the square of Eq.(16),the line(square)is to Eq.(12).

4.The optimal amplitude estimation

On the one hand,the estimation of p in Eq.(13)can be regarded as a single-parameter estimation problem since the phase φ is known.Therefore,the maximum likelihood estimation method can be applied to solve this problem.On the other hand,the thermal fluctuation torque is a white noise process and the autocovariance operator Eq.(3)is diagonal.Considering the above two points,we apply the equation-of-motion filter operator Ω to obtain the optimal estimation for thermal noise.Firstly,we must derive the optimal estimation formula for white noise.

4.1.The optimal amplitude estimation for white noise

Substituting θth(t)by θwhite(t),note that θwhite(t)has the same statistical characters as the thermal fluctuation torque:

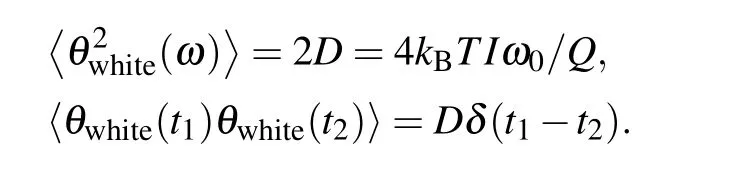
Equation(13)can be rewritten as

where θs(t,p)=pcos(ωst+φ)and t ∈[0,tm].The likelihood function of θn(t)is

By making the first derivative function of the logarithm of Eq.(18),the maximum likelihood estimation of p can be obtained by

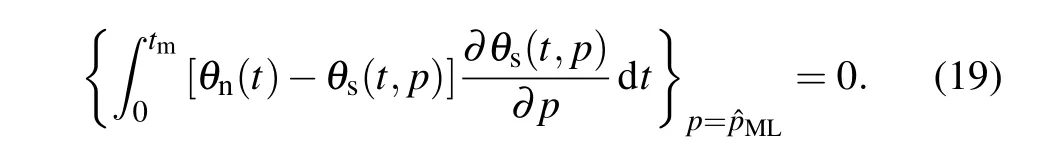
Generally,we often use the Cramér–Rao lower bound(CRLB)as the minimum variance of the unbiased estimator.[18]To obtain the CRLB of the maximum likelihood estimator in the presence of white noise,we make the second derivation of Eq.(18)and calculate the expectation of it. The CRLB of this method can be written in the form

Substituting θs(t,p)=pcos(ωst+φ)into Eq.(19),we have

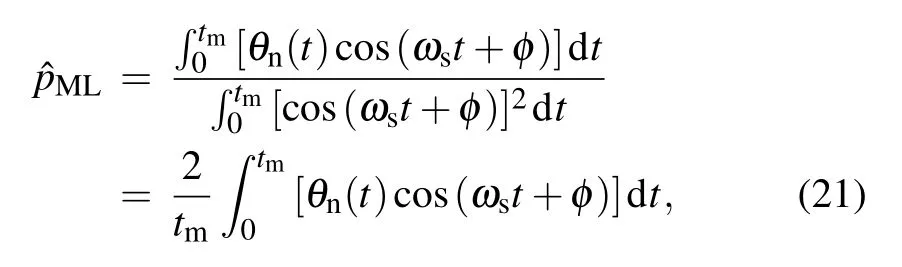
which has the same derivation as the correlation method.The expectation and variance ofcan be calculated asandrespectively.In addition,we found that the variance ofis in agreement with the result of Eq.(20).It means that maximum likelihood estimation method and the correlation method are unbiased amplitude estimator with the minimum variance for white noise.For the convenience of further calculation,we give the maximum likelihood estimating function

where Θ(t;0,tm)=u(t)−u(t −tm)and u(t)is the step function.

4.2.The optimal amplitude estimation for thermal noise

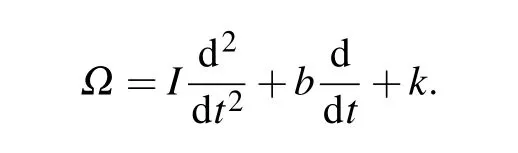
Therefore,equation(21)can be rewritten when working in the torque basis

It has to be mentioned that the transformation to the torque basis removes the information about the boundary conditions.[19]This will be considered later. Definingand taking the integration by parts,we have

where

The maximum likelihood estimating function in the torque basis can be calculated as

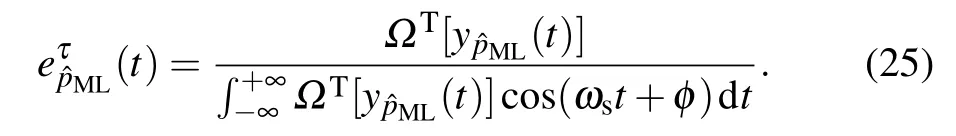
where u(t)is the step function,δ(t)is the impulse function and δ′(t)is the first derivative of the impulse function.Inserting the result into Eq.(25)leads to

Therefore,we can obtain the final form of Eq.(24)

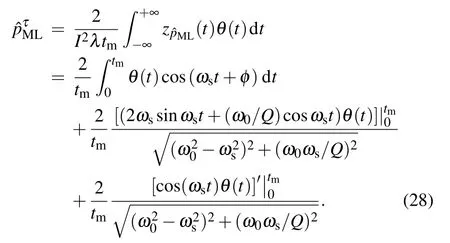
The relative variance also can be calculated in the torque basis.Equation(28)can be rewritten as

where

with the variance

Now we discuss the boundary conditions as mentioned before. Because the thermal fluctuation torque that acts on a torsion pendulum is uncorrelated for two different times,the initial position,initial velocity,and the acting forces completely determine the twist of the pendulum.But the amplitude is different from the displacement in Ref.[19]the initial position and initial velocity contain no information about it.So the maximum likelihood estimator and the relative variance are Eq.(28)and Eq.(31),respectively.Note that the variance of the estimator has come to the CRLB,which means that the estimator is optimal. Furthermore,equation(31)equals Eq.(12),which is an important check for the formula of the least detectable torque.

However,equation(28)cannot be used for experimental data directly. By cutting the measurement time into m periods and further calculation,we can extract the magnitudes of the coefficients ajand bj(j=1,2,...,m)at the j-th period according to the following equations:

where

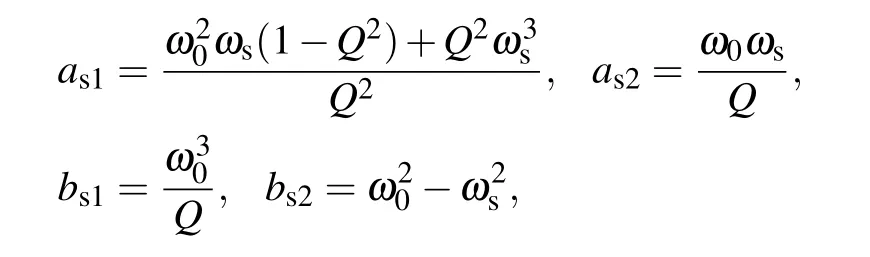
with the uncertainties of ajand bj

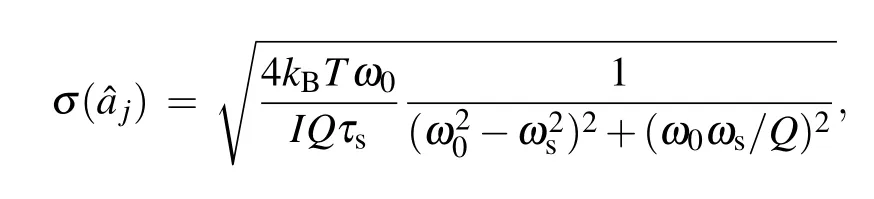
Then the final uncertainties of p can be obtained by

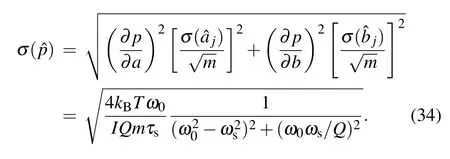
It can be seen that the variance also come to limit by the above procedure.Different from the correlation method,the maximum likelihood estimator can meet the minimum variance without limitation of the measurement time. To be stressed,the thermal noise must be the leading noise.To validate the expression derived,we first performed the numerical simulation.The numerical results is in good agreement with our theoretical result.Then,we apply the method to process an experimental data set on the basis of the numerical simulation.

5.Application

We will apply our method to process the experimental data in determining the amplitude of the gravitational calibration signal of tesings the ISL by HUST.In the experiment,the level of noise is greatly reduced with a good experimental platform.The measurements are made at levels near the thermal noise floor of instruments.The parameters are the same as mentioned in Section 3.Figure 2(a)shows the time-domain figure of the raw signal with the sample interval of ∆t=1 s.The length of the raw data is about 23 h. The corresponding power spectrum density(PSD)of the raw data is shown in Fig.2(b),we can see that the low frequency noise is close to the thermal noise limit of the pendulum.The most significant features are that the raw data have a monotonic drift and the free torsional oscillation.

Fig.2.(a)The raw data of determining the amplitude of the gravitational calibration signal.(b)The solid curve is the corresponding PSD of the raw data,and the dashed line is using the mean-square spectral density of the thermal fluctuation Eq.(4). The data are collected continuously from 17 November 2014 to 18 November 2014.

Firstly,we suppressed the monotonic drift by using a quadratic function fitting,which can be realized with a mathematical algorithm.Then,we applied a digital filter to remove the free torsional oscillation.The“notch”filter is adding the data to itself at one half oscillation period,which was proposed by the Eöt–Wash group.[24]It can be written as

where θ(ti)is the series of the sample data and T0is the torsional period.Figure 3(a)shows the filtered data.The corresponding PSD of the filtered data is shown in Fig.3(b),we can see that the torsional period of the pendulum and the monotonic drift have been suppressed greatly.Following the above steps,the data can be written as Eq.(13),so our method can be applied for the filtered data.By separating the filtered data into m signal periods,we can extract the magnitudes of the coefficients a j and bj(j=1,2,...,m)at the j-th period with the correlation method Eq.(14)and the optimal estimator Eq.(32).The statistical errors of the sequences{aj}and{bj},respectively,expressed by whereandare the mean value of the sequences{aj}and{bj},respectively.The amplitude of the calibration signal p and its uncertainty can be expressed as follows:

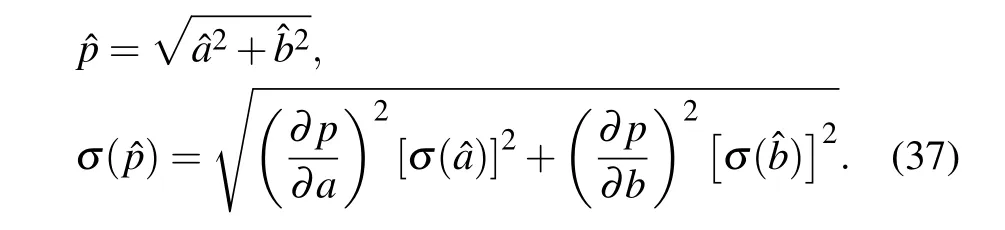
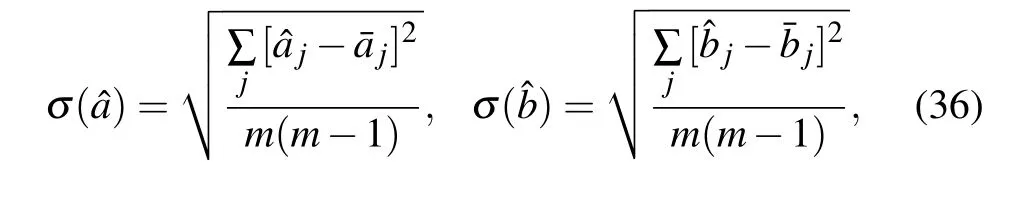
Fig.3.(a)The data of suppressing the free torsion oscillation.(b)The solid curve is the corresponding PSD of the filtered data,and the dashed line is fitting to Eq.(4).

After the above steps,we can obtain the uncertainty of different estimators as a function of the sample time.Figure 4 shows the comparison of the uncertainty of the optimal estimator with that of the correlation estimator and the thermal limit,obtained by performing Eqs.(12)and(37).The thermal limit can be regarded as the criterion of selecting the best estimator. From Fig.4,we can see that the uncertainty in the optimal estimator has been improved than the correlation estimator and the uncertainty in the optimal estimator changes more smoothly as the sample time is decreasing.The corresponding measurement time and uncertainty are listed in Table 1. As expected,the measurement time with the optimal method has been reduced half than before for the same uncertainty.These results prove that our method is better than the correlation method in determining the amplitudes,especially when the observed time in the experiment is limited.Hence,the results of processing experimental data are in agreement with the expectation of our model and the difference in statistical characters of thermal noise and white noise for the torsion pendulum is worth considering in pursuit of higher precision.

Fig.4.A plot of the uncertainty of the thermal limit(circle),the correlation method(diamond),and the optimal method(square)as a function of sample time in processing the filtered data.The optimal estimator changes smoothly as the sample time is decreasing.The gap between the optimal estimator and thermal limit is almost the same for different sample time.

Table 1.The comparison of the uncertainty with two different methods in our experiment and the thermal limit.It also shows the corresponding measurement time and the number of the signal periods.

6.Summary

In the gravitational experiments with torsion pendulum,by using the correlation method based on the Fourier transform,we found that this variance does not decrease monotonically with increasing measurement time tm.Furthermore,there exists the gap which is caused by the difference in statistical characters of thermal noise and white noise for the torsion pendulum.In pursuit of higher precision and a shorter measurement time,we must fill with the gap between the method and the thermal noise limit.In this paper,we proposed an optimal method based on the maximum likelihood estimation and the equation-of-motion filter operator. We have shown that,for thermal noise,the variance of the optimal method can reach the thermal limit of the torsion pendulum without limitation of the measurement time.In Section 5,the results of processing experimental data show that the optimal method can improve the precision of determining the amplitude of signal. Especially,if the observed time in the experiment is limited,the advantage of the new method will be more prominent comparatively. Namely,the measurement time with our method can be reduced about half than before for the same uncertainty,which means that there is no direct benefit from a longer measurement for thermal-noise-limited experiments where the measurements meet the design requirements.[19]This result has implications for the experimental design and for the reduction of measurement time.However,it must be point out that the optimal estimator is not completely consistent with the thermal limit in dealing with the data sequence.Because the noise background of a physical system is generally a superposition of several noise processes,[19]such as the twist angle readout noise,the rotation noise,and so on. The statistical characteristics of the noise have not been fully understood so far. In addition,there are several systematic effects that we have not considered,like fiber inelasticity or nonlinearity and linear fiber drift.These will be fully discussed in a subsequent article.