Robust two-gap strong coupling superconductivity associated with low-lying phonon modes in pressurized Nb5Ir3O superconductors∗

Bosen Wang(王铂森),Yaoqing Zhang(张尧卿),Shuxiang Xu(徐淑香),Kento Ishigaki,Kazuyuki Matsubayashi,Jin-Guang Cheng(程金光),4,Hideo Hosono,and Yoshiya Uwatoko

1Beijing National Laboratory for Condensed Matter Physics and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2Institute for Solid State Physics,University of Tokyo,Kashiwanoha 5-1-5,Kashiwa,Chiba 277-8581,Japan

3Materials Research Center for Element Strategy,Tokyo Institute of Technology,Yokohama 226-8503,Japan

4Songshan Lake Materials Laboratory,Dongguan 523808,China

Keywords:new superconductor,high-pressure effect,strongly coupled superconductor

Low energy anharmonic lattice vibration significantly affects electron–phonon coupling(λe−p)and plays an important role in exploring superconductors(SC)and revealing superconducting mechanism.[1,2]Among them,phonon softening associated with structural instabilities usually results in Fermi surface nesting and the enhancement of the electron–phonon coupling,which is believed to be much important for superconducting pairings.[3–7]Various cage-like materials have been reported and attracted much more attention.[3,6,7]The commonalities are composed of hollow covalently bonded atomic clusters and various inserted elements,offering playgrounds to explore diverse structures,exotic physics,and multifunctionalities,e.g.,multi-band SCs,[3,8–10]metal–insulator transition,[10]thermoelectricity,[11]and electrides.[12,13]But some regularity is not universal concerning the superconducting pairing mechanisms,which is also challenging to study these scientific issues.

Hexagonal structure Mn5Si3-type derivatives are such examples.[14,15]One of the top priorities is the explorations of new SCs and superconducting mechanisms.[15–19]At present, the difficulty in synthesizing single-phase hexagonal and tetragonal materials lies in their close formation energies.[16,17,19]One common way is elementary intercalation into interstitial positions of Mn5Si3Mx(M=carbon,nitrogen,oxide,and transition metal elements,etc).[14–19]Hexagonal phase can be stabilized and the relevant studies are performed to reveal the relationships between lattice instabilities and superconductivity. For example,hexagonal Nb5Ir3is stabilized upon the insertion of the interstitial oxygen and Tcis increased as a result.It is sure that the interstitial oxygen brings great changes in electronic structures.[16]It still remains unclear whether the enhanced Tcis dominantly associated to the volume change,band fillings,structural instability,and/or disorders.[16]Another issue to be addressed is the relationship of electride and superconductivity. Theoretical calculations predicated that the electride nature of Nb5Ir3vanishes in Nb5Ir3O.As we know,eletride materials have electronic bands of anionic electron near Fermi level(EF)in many cases including C12A7: e-1 electride,Ca2N,and Y5Si3,which is the important reason why electride materials exhibit interesting properties.For SCs,Tcis enhanced along with the suppression of the electride nature and the coexistence of superconductivity and electride is firstly reported with Tc∼0.16–2.4 K.[12,13]For C12A7:e-1 electride SC,Tcis increased to 2.4 K by pressure and this enhancement is attributed to the changes in electronic nature of anionic electride band crossing Fermi levels switching from s-to sd-hybridized state.[13]However,the interstitial oxygen suppresses superconducting state in other cases,hexagonal Zr5Sb3is superconductive at ∼2.3 K,but Zr5Sb3O is not superconducting above 1.8 K,it is thought that larger density of states(DOS)at EFassociated with the Zr-d electrons and the larger value of λe−pis critical.[15]Analogously,in Zr5Sb(3−x)Rux,its hexagonal structure transforms into W5Si3-type one for 0.4 ≤x ≤0.6.Tcincreases from 2.3 K to 5 K in Zr5Sb2.4Ru0.6,which originates from the EFclose to the DOS peak.[17]Except for these above scientific issues,the present studies on the intercalated Mn5Si3-type materials focus on macro-correlations of crystal structure and superconductivity,and some conclusions are inadequate. In this work,Nb5Ir3O is selected to study the issues further. Another concern is to reveal superconductivity by comparative analysis of doping and high pressure,and to judge whether unconventional or not with magnetism of localized and/or itinerant iridium.[20,21]

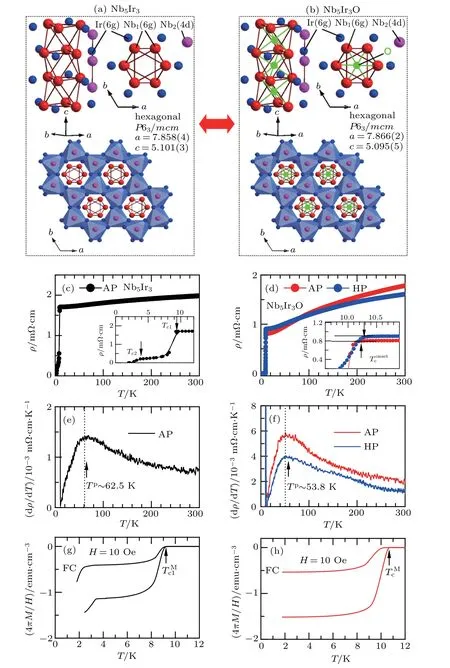
Fig.1.Crystal structures for(a)Nb5Ir3 and(b)Nb5Ir3O.ρ(T)for(c)Nb5Ir3 and(d)Nb5Ir3O.The enlargement of low-T data is shown in the inset.The derivative dρ/dT for(e)Nb5Ir3 and(f)Nb5Ir3O.The broad peaks are marked by T p.M(T)curves at 10 Oe under the ZFC and FC processes for(g)Nb5Ir3 and(h)Nb5Ir3O.

High pressure is an effective and clean way to study structural chemistry and electronic phase transitions of materials by shortening bonds and reconstructing electronic bands.For SCs,high-pressure effect is valuable because the underlying mechanism can be identified by analogizing with the known SCs. In this work,Nb5Ir3O is found to be a strongly coupled SC with two s-wave gaps and phonon softening associated with interstitial oxygen is critical.

At ambient pressure(AP),electrical transport and specific heat of Nb5Ir3and Nb5Ir3O were measured on commercial physical properties measurement system(PPMS,1.8 K≤T ≤300 K,−9 T ≤H ≤9 T).High-pressure susceptibility was measured in a piston-cylinder cell with glycerol as the pressure transmitting medium(PTM)and a small piece lead as the pressure monitor.The background contributions mainly originate from Meissner signal of Pb reference.High-pressure electrical transport was performed by the four-probe method in a cubic anvil pressure cell which generated the hydrostatic environment.[22]MgO cubes were used as the gasket and glycerol as PTM.All the measurements were carried out in4He refrigerated chambers(1.9 K ≤T ≤300 K).

Structures of Nb5Ir3and Nb5Ir3O(1−δ)are shown in Figs.1(a)and 1(b).They have similar hexgonal symmetry except for the interstitial oxygen inserted.Nb5Ir3contains two groups of weakly connected octahedra along the c axis:one is hollow(Nb1)6octahedron connected by Nb1–Nb1 bonds,the other is side-sharing Ir(Nb2)6octahedron.Moreover,it is regarded as the network of twisted trigonal Nb1-prisms connected by the planes along the c axis,which allows the insertion of oxide ion in the“Nb1 cages”.It does not change the crystal structure,but forms covalent bonds Nb1–O.Upon changing from Nb5Ir3to Nb5Ir3O,lattice parameter c contracts by ∼0.11%while a and b expand by ∼0.087%. In Figs.1(c)and 1(d),ρ(T)of Nb5Ir3and Nb5Ir3O shows the metallic behavior. Two independent drops appear in the inset of Fig.1(c),which represent superconducting transitions of hexagonal and tetragonal Nb5Ir3,respectively.[20,21]andare marked where ρ(T)deviates linearly and is zero.At AP,is ∼9.4 K for hexagonal Nb5Ir3and ∼4.0 K for tetragonalis ∼10.15 K and∼is 10 K for Nb5Ir3O.In Fig.1(d),ρ(T)is shown and similar in temperature dependence for both as-grown Nb5Ir3O and annealed one(4 GPa,600◦C).A clear difference is that high pressure broadens the transition anddecreases from ∼10 K to ∼9.6 K.A broad peak appears in dρ/dT at a critical temperature Tp,which decreases from ∼62.5 K to ∼53.8 K upon the increase of the interstitial oxygen. Usually,this peak reflects the information of the phonon spectrum and is closely related with Debye temperature θD.[23]

Fig.2.The transverse resistivity ρxy vs.H at various temperatures:(a)S1#and(b)S2#.(c)Temperature dependence of Hall coefficient RH(T).

Figure 2 displays the field-dependence of transverse resistivity ρxyat various temperatures up to 5 T.ρxyshows a linear H-dependence for each temperature. Hall coefficient RHis defined by dρxy/dH. RHis positive and almost temperature independent below 200 K,and negative above 250 K,which suggests the balance of electron-to hole-types carriers with different effective masses and velocities.Its strong temperature dependence elucidates that Nb5Ir3O has a complex multi-band electronic structure with both electron-and hole-Fermi pockets.[24,25]According to the successive changes in mangetism and electrical resistivity,we can exclude the possible structural and magnetic phase transitions.Besides,the longitudinal resistivity ρxxis measured,the magnetoresistance MR=∆ρxx/ρxx(0)=(ρxx(5 T)−ρxx(0))/ρxx(0)<2%. As we know,for a multi-band structure material,it is difficult to calculate the carrier concentration by a single-band model.It is necessary to consider the mobility of two carriers and the specific Fermi surface structures and more theoretical calculations and in-depth experimental analysis are needed.Meanwhile,the carrier density by the simple estimate of the singleband model is only a lower limit of the total carrier number(electrons plus holes),such as n ∼1.6×1028m−3for Nb5Ir3O at 300 K.Considering the change of sign of RH,the compensation effect at 300 K(where the one-band carrier density was calculated)is expected to still be significant.Further understandings need De-Haas–van Alphen and angle-resolved photoemission spectroscopy.

Temperature dependence of specific heat Cp(T)is shown in Fig.3(a). On warming,Cp(T)increases and approximates 3NR above 300 K.Tc(∼9.94 K)is marked by the jump in Cp/T.The inset shows Cp(T)/T and its polynomial fittingsin the temperature range of Tc≤T ≤14 K,where γnT andare electron and phonon contributions,respectively. It gives γn=34.255 mJ/mol·K2,β1=0.4489 mJ/mol·K4,β2=1.07×10−3mJ/mol·K6. Electronic contribution Ce(T)was investigated by the deduction offrom Cp(T)as in Fig.3(c). The ∆C/γnTcat Tcis ∼1.91,larger than 1.43 for a Bardeen–Cooper–Schrieffer(BCS)SC.[26]λe−pis 0.85 by using McMillan formula Tc=(θD/1.45)exp{−1.04(1+λe−p)/[λe−p−0.15(1+0.62λe−p)]}, which implies strong electron–phonon coupling.[26]

Fig.3.(a)Temperature dependent Cp(T)for Nb5Ir3O,the inset shows low-T Cp(T)/T.(b)Theis the sum of Debye model CD and Einstein oscillators CE.(c)Electronic specific heat Ce(T)=Cp(T)−(β1T 3+β2T 5)is analyzed by using a single-gap model as Ce(T)/T=β1T 3+β2T 5+Bexp(−∆/kBT).(d)and(e)H-dependence of Cp(T).(f)The upper critical field Hc2 is given by Hc2(T)=Hc2(0)[1−(T/Tc)2]/[1+(T/Tc)2]and Hc2(0)=−0.693Tc dHc2/dT,respectively.Inset shows H-dependent γ(H)and its comparison to H1/2-behavior for d-wave SCs.

To get more information on gap symmetry,Ce(T)was analyzed by a single-gap model C(T)=β1T3+β2T5+Bexp(−∆/kBT)at first,which gives 2∆/kBTc=4.25. But clear deviations between experimental and mathematical fitting exist for T<5 K,which implies that isotropic s-wave is too simple. Meanwhile,an anisotropic s-wave gap is similar but not applicable to the present case. Then,two anisotropic s-waves with gaps ∆1and ∆2are required. The data are well duplicated with 2∆L(0)/kBTc∼6.56(90%)and 2∆S(0)/kBTc∼2.36(10%). Furthermore,H-dependence of Ce(T,H)is measured. At H=0,the linear extrapolation of Ce/T vs.gives a“residual”Sommerfeld coefficient γ0≈0 mJ·mol−1·K−2.For each H,γ(H)at T=0 K is determined by linear fitting to Ce/T vs.T2.The H-dependence of γ(H)is plotted in Fig.3(f). γ(H)increases linearly as a function of H,implying the appearance of nodeless gap.γ(H)is smaller than the H1/2dependence for d-wave SCs with line nodes.[27]Generally,in fully-gapped SCs,the excited state is seen as normal-state quasiparticles in vortex core states,which generates the γn(H)≈H at zero temperature. Thus,Nb5Ir3O is a fully-gapped s-waves SC.Moreover,using the Hdependence ofCp(T)data in Figs.3(d)and 3(e),the upper critical field Hc2(0)is 10.5(5)T and 9.5(8)T by Ginzburg–Landau equation Hc2(T)=Hc2(0)[1 −(T/Tc)2]/[1+(T/Tc)2]and Werthamer–Helfand–Hohenberg(WHH)formula Hc2(0)=−0.693TcdHc2/dT,respectively.[28]

To extract phonon contributions,thevs.T is plotted.It shows a broad peak at ∼23 K,which manifests the existence of low-energy Einstein vibration associated with anomalies in the phonon spectrum.[29]Cp(T)is the sum of Debye mode and Einstein oscillators

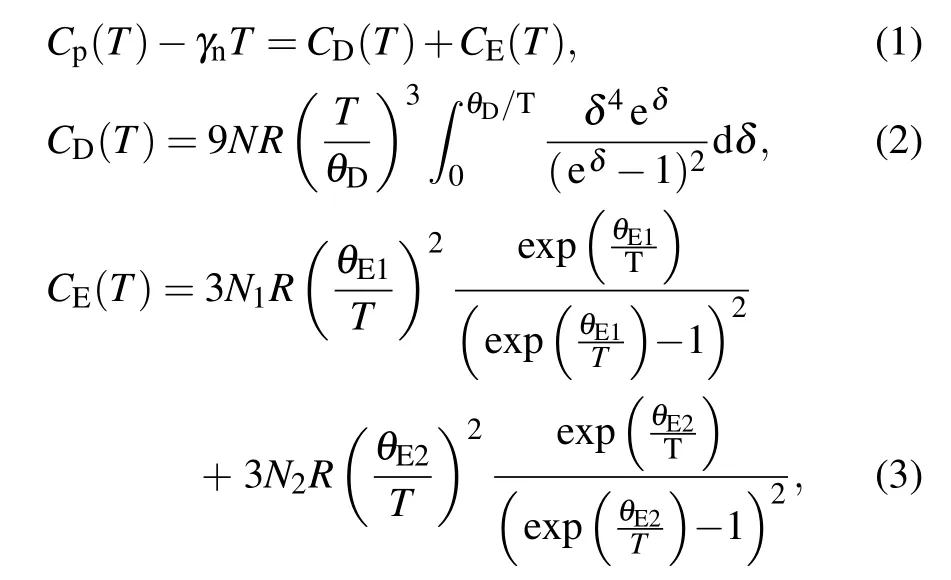
where CD(T)and CE(T)are the contributions of continuous phonon mode and localized oscillators,respectively,N,N1,and N2are the numbers of oscillators per formula,R is the gas constant,θDand θE1,θE2are Debye and Einstein temperatures,respectively.It gives θD=315.8(4)K,θE1=87.9(2)K,θE2=69.7(5)K,which are insensitive to the temperature ranges selected.As above,the Nb1O octahedron is connected with side-sharing Ir(Nb2)6one,which reminds us that Tcdepends on λe−pin materials with low-lying phonon modes.It suggests the existence of phonon softening associated with interstitial oxygen.

Figure 4 shows ρ(T)of Nb5Ir3O under various pressures.With increasing pressure,room-temperature ρ decreases and its value at 13 GPa is nearly three times smaller than that at AP.ρ(T)has similar temperature dependence for each pressure:metallic behavior and entering into superconducting state.As shown in Fig.4(b),with increasing pressure,anddecrease and transition widthincreases,implying that the superconducting transition is broadened by pressure.As shown in Fig.4(c),susceptibility is measured in a piston pressure cell.is determined by the intersections of two straight lines. Large field shielding effect belowconfirms bulk superconductivity.The fraction is nearly 1 by subtracting the background contributions of Pb signal which is about 5%–10%of total magnetization.decreases from∼9.91 K at 0.10 GPa to ∼9.70 K at 1.21 GPa.The stress effect and the enhanced anisotropy by pressure are the main reasons.Besides,the broad peak at T p ∼53.8 K atAP enhances to 69.4 K at 13 GPa,which is negatively correlated with Tc.

Fig.4.(a)The ρ(T)under various pressures.(b)Low-T ρ(T)is enlarged and dρ/T in the inset.(c)M(T)under ZFC process at 10 Oe.(d)∆ρ(T)under various pressures and the characteristic temperatures T ∗,T ε,and T#are defined as the crossing points from T 2-to T 3-dependence,the deviation from T 3-dependence,the intersection of T 3-dependence and linear fitting,respectively.The parameters are summarized with pressures:(e),(h)ρ300 K,ρ0,(i)the A value.

Normal-state ρ(T)is analyzed bywith residual resistivity ρ0,temperature coefficient A,and exponent n.It is found that n is ∼2.±0.1 for T ≤T∗,then increases up to ∼3.±0.1 for T∗≤T ≤Tε,and then tends to saturation for T ≥T#,where T∗,Tε,and T#are defined as the crossing points of T2-to T3-dependence,the deviation from T3-dependence,the intersection of T3-dependence and linear fitting above 250 K,respectively.All the parameters are shown in Figs.4(f)and 4(g).Considering the small pressure difference and distribution(<0.5 GPa)in the cubic anvil cell cooling from 300 K to 2 K,the present analyses of temperature dependence of resistivity are reliable.increases as the pressure increases while T∗reaches the maximum at 8 GPa.T2-fittings for Tc≤T ≤T∗give ρ,A and their pressure dependence in Figs.4(h)and 4(i).Both ρ and ρ300Kreduce with increasing pressure.The decrease of ρ is attributed to the weakened grain boundary scatterings under pressure.The A has a positive correlation with Tc:it decreases quickly below 4 GPa,and then trends to a constant.

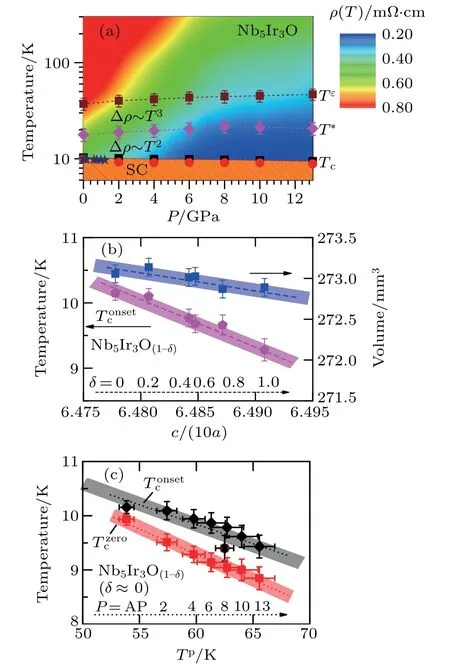
Fig.5.(a)Pressure phase diagram,the color represents the changing trends of resistivity. (b)The the unit-cell volume V,and the lattice parameter ratio c/(10a)are related with the increasing nominaloxide content(1−δ)of 0,0.20,0.40,0.60,0.80,1.0 for (c)We scaled the relationship of and for The thick lines indicate the tendency.

In Fig.5(a),we outline the high-pressure phase diagram.The color represents the changing trend of resistivity. Generally,T2-dependence for Tc≤T ≤T∗shows that electron–electron scattering is the main source and T3-dependence forindicates important electron–phonon scattering.Above Tε,ρ(T)is saturated,indicating that electron–phonon scattering is comparable to the atomic lattice spacing.Thus,the increases of characteristic temperatures reflect the change of phonon contributions.[23,26,30]For,theunit-cell volume,and lattice parameters c/(10a)ratio are summarized in Fig.5(b). With increasing(1 −δ),increases from ∼9.4 K to ∼10.15 K in Nb5Ir3O,the volume expands from ∼272.89 mm3to ∼273.05 mm3,and c/(10a)decreases from ∼0.649 to ∼0.647.More interestingly,and the volume have similar linear dependence on c/(10a).In Fig.5(c),the relationship ofandis also scaled.Bothanddecrease linearly with Tp.It is argued thatis proportional to the parameters closely correlated with θD,which implies that phonon contributions are different with pressures,[23,26]e.g.,the weakness of phonon scattering and the reduced value of λe−p.[5,15,17]

Finally,we discuss the evolution of superconditing transition temperature with the interstitial oxygen and pressures.As mentioned above,with increasing concentration of the interstitial oxygen,the volume expands and Tcenhances,which seems to contradict with pressure.[16]Under pressure,Tccorrelates with the A value directly. As we know,A is proportional to the square of Sommerfeld coefficient,as an important measure of DOS at EF.Therefore,the decrease of Tcmainly originates from the reduce of N(EF),which is consistent with the phonon-mediated behavior in Nb5Ir3O.Previous studies revealed that Tcwill be higher if with larger N(EF).[15,17–19]It suggests that band filling effect is the main result of superconductivity.Or to say,high pressure and interstitial oxygen change the electronic structure and phonon spectrum in different ways.Several possible scenarios are proposed:the first case is that pressure broadens energy bands and results in the decrease of N(EF).[26]It is consistent with the fact that Nb5Ir3O is phonon-medicated SC.For Nb5Ir3O(1−δ),the monotonic increase of N(EF)may account for higher Tcwith increasing concentration of the interstitial oxygen.The second scenario is the weakness of λe−punder pressure,which can reduce Tc.[1,2]This is basically consistent with strong correlation characteristics of these SCs.[3,7,8,10]For Nb5Ir3O(1−δ),considering the strong electronegativity of oxygen,the insertion of interstitial oxygen introduces Nb1–O ionic bonds,which may enhance the electron correlations and λe−p.The third scenario is that Nb5Ir3O has an inter-band coupling considering its multi-band electronic structure,which usually appears in other multi-band SCs.[31,32]For Nb5Ir3O(1−δ),the insertion of interstitial oxygen enhances this coupling and results in an enhancement of Tc,which is in good agreement with theoretical calculations.To understand the details,further studies on band structures and phonon spectrum are also required.

In summary,we have investigated robust superconductivity and gap symmetry of Nb5Ir3O.Nb5Ir3O is found to be strongly coupled phonon-medicated SC with double s-waves.Phonon softening and low-lying phonon modes associated with the interstitial oxygen are critical to understand the evolution of Tc.

Acknowledgment

We thank S.Nagasaki and Dr.Gouchi for the technical assistance.