负径向电场对带电粒子俘获率影响的数值模拟

钟翊君，龚学余,*，黄千红，谭清懿，龚 蕾，杜 丹

(1.南华大学，湖南 衡阳 421001；2.福清核电站，福建 福清 350300)

高温等离子体的约束和辅助加热是实现受控热核反应的基本问题。自从ASDEX[1]首次在托卡马克上发现改善约束性能的H模后，大量实验和理论研究表明，由负径向电场引起的等离子体极向旋转速度的急剧增加是诱发L-H模转化和改善约束性能的重要原因[2-6]。在托卡马克磁场位形下，相同能量的电子和离子，由于离子在磁场分布不均匀引起的梯度漂移和曲率漂移作用下产生的跨越磁面的运动比电子的大，从而形成电子和离子相对分离，有些边界离子还会损失出等离子体区域，在边缘出现净电子，净电子的空间分布会在边缘产生一个负的径向电场。与此同时，由于负径向电场的产生，带电粒子运动过程中增加了一个较大的电漂移，反过来影响电子和离子的运动轨迹和约束性能。因此，关于负径向电场存在时，粒子运动情况的研究是磁约束聚变等离子体研究领域的重要问题。另一方面，电子俘获率在电子回旋波电流驱动和功率沉积的研究中有着重要意义，俘获电子会吸收更多的波功率，使波功率的沉积更加集中，并使电流驱动效率明显降低[7-9]。同时，在中性束注入下快离子产生的自举电流[10-11]及低杂波电流驱动和功率沉积等的研究中，也需先知快离子的俘获率。然而，对于负径向电场存在时俘获率的计算尚未见相关报道。

本文采用有限元法和高斯迭代法[12-13]，结合实验测得的中心边缘密度、温度，等离子体总电流及中心电流密度，数值求解平衡方程[14]，得到等离子体磁场，从而模拟氘离子在负径向电场存在时的运动轨迹，然后采用蒙特卡罗方法抽取满足麦克斯韦速度分布的氘离子速度样本，统计氘离子的俘获率，研究负径向电场对氘离子俘获率的影响。

1 物理模型

1.1 平衡位形的求解

结合EAST装置实验平衡数据，采用有限元法和高斯迭代法求解Grad-Shafranov方程[14]，计算轴对称等离子体平衡位形下的磁通分布：

(1)

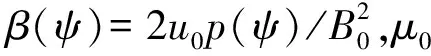
p(ψ)和g(ψ)2均可表示为关于角向磁通的多项式形式：

(2)

(3)

其中：n为电子离子密度；ti、te分别为离子、电子温度；nc与ne分别为电子和离子的中心密度与边缘密度；ψc为中心角向磁通；tec、tic分别为电子和离子的中心温度；tee、tie分别为电子和离子的边缘处温度；b1和b2为常数。

为了解式(1)，式(2)、(3)中的参数必须被确定。先假定一个中心角向磁通ψc，然后假定b1和b2的初值，最后用有限元法进行网格剖分，用程序求出的总电流、中心电流密度和实验可间接测得的总电流Ip、中心电流密度j0相等以及程序求出的中心角向磁通和假定的中心角向磁通相等做迭代条件，反演出与实验相符合的b1、b2和ψc。

由上述方法可得到各网格点的环向电流密度和极向磁通等物理量，间接求出平衡位形下各点的磁场：

(4)

其中，B为磁场。

1.2 带电粒子运动轨迹的求解

粒子在托卡马克位形中运动，满足洛伦兹力方程：

(5)

其中：m为质量；v为速度；t为时间；q为带电量；E为电场；B为磁场，通过式(4)得到，直角坐标系中，磁场采用(Bx,By,Bz)表示，具体对应关系示于图1。

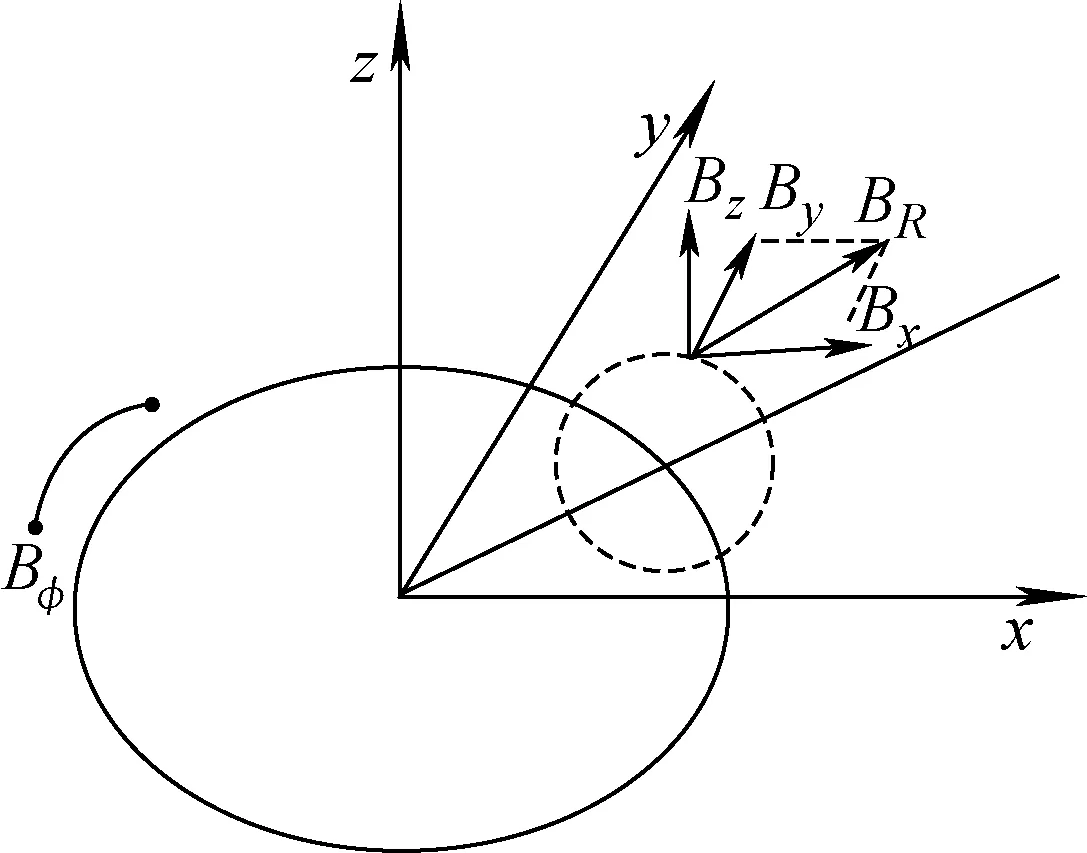
图1 磁场分布Fig.1 Magnetic field distribution

托卡马克中粒子运动方程可表示为：

(6)

负径向电场Er表示为：

其中：E0为常数；r为径向位置。用四阶龙格库塔方法求解式(6)，计算平衡位形下各点的带电粒子运动轨迹。

2 数值模拟结果与分析

2.1 氘离子在平衡位形中的运动轨迹

根据上述理论，首先采用EAST装置(炮号33068)的放电数据(R=1.8 m，a=0.45 m，Ip=0.5 MA，j0=1.5 MA·m-2，中心处的环向磁场Bt=2.0 T，nc=3×1019m-3，ne=1×1018m-3，tec=3 keV，tic=2 keV，tie=tee=0.1 keV)求解式(1)，得到平衡位形。然后根据式(4)计算截面各网格点的磁场，最后采用龙格库塔方法求解式(6)，模拟氘离子在托卡马克电磁场中的运动轨迹。带电粒子在托卡马克电磁场中的运动是以速度vm沿螺旋磁力线的移动加上由磁场不均匀性引起的曲率漂移和梯度漂移合成速度vDB以及电场引起的电漂移速度vE所带来的运动。其中vDB在该平衡位形中离子的漂移方向是向上的，vE在该平衡位形中离子的漂移方向是沿极向磁场反方向的。图2示出不同负径向电场下氘离子的运动轨迹在小环方向上的投影，氘离子初始位置(x0，y0，z0)=(2.227 5 m，0，0)，初始速度(vx，vy，vz)=(0，1.65×105m/s，0)。图2a中轨迹1为通行粒子扩张轨迹，轨迹2为外翻香蕉粒子轨迹，轨迹3为内翻香蕉粒子轨迹，轨迹4为通行粒子扩张轨迹。由图2a可看出，随负径向电场的增大，氘离子轨迹由扩张通行轨迹向外翻香蕉轨迹再向内翻香蕉轨迹，最后向压缩通行轨迹演变。图2b中速度vmE表示离子沿磁力线方向的运动速度vm与电场引起的电漂移速度vE的合成速度，与图2a所示轨迹相互对应。轨迹1、2所代表的氘离子由于洛伦兹力从初始点开始往赤道面以上运动，加上向上的vDB，离子的运动轨迹在初始磁面外出现扩张轨迹。轨迹3和4所代表的粒子从初始点开始往赤道面以下运动，加上向上的vDB，离子的运动轨迹在初始磁面内出现压缩轨迹。轨迹2的合成速度小于轨迹1的，于是氘离子轨迹由通行轨迹向香蕉轨迹演变。

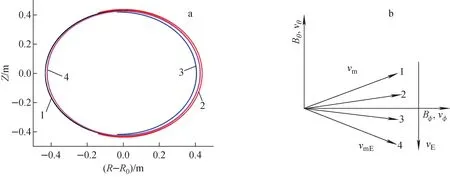
1——E0=0 V/m；2——E0=15 000 V/m；3——E0=30 000 V/m；4——E0=80 000 V/m图2 初始速度(vx，vy，vz)=(0，1.65×105 m/s，0)时氘离子运动轨迹在小环方向上的投影(a)及速度合成(b)Fig.2 Projection of poloidal cross-section of deuterium ion orbit (a) and velocity compose (b) under initial velocity (vx, vy, vz)=(0, 1.65×105 m/s, 0)

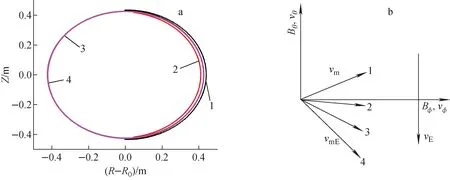
1——E0=0 V/m；2——E0=15 000 V/m；3——E0=30 000 V/m；4——E0=80 000 V/m图3 初始速度(vx，vy，vz)=(1.34×105 m/s，6.7×104 m/s，6.7×104 m/s)时氘离子运动轨迹在小环方向上的投影(a)及速度合成(b)Fig.3 Projection of poloidal cross-section of deuterium ion orbit (a) and velocity compose (b) under initial velocity (vx, vy, vz)=(1.34×105 m/s, 6.7×104 m/s, 6.7×104 m/s)

图4示出初始位置(x0，y0，z0)=(2.227 5 m，0，0)、初始速度(vx，vy，vz)=(-1.34×105m/s，-6.7×104m/s，-6.7×104m/s)的氘离子在不同负径向电场下氘离子的运动轨迹在小环方向上的投影及速度合成。图4中轨迹1为无负径向电场下的氘离子轨迹，初始入射角大，从初始位置开始沿磁力线负方向做回旋运动，受向上的漂移速度vDB的影响，形成内翻香蕉粒子轨迹。负径向电场为15 000 V/m时，粒子运动速度增加，形成压缩的通行轨迹。当负径向电场进一步增加时，依然为压缩的通行轨迹。

图5示出初始位置(x0，y0，z0)=(2.227 5 m，0，0)，初始速度(vx，vy，vz)=(0，-1.65×105m/s，0)的氘离子在不同负径向电场下氘离子的运动轨迹在小环方向上的投影及速度合成。图5中轨迹1为无负径向电场下的氘离子轨迹，初始入射角小，为压缩的通行粒子轨迹。加入负径向电场时，依然为压缩的通行轨迹。

2.2 氘离子俘获率计算

托卡马克中，带电粒子运动速度整体上满足麦克斯韦分布，其分布函数形式为：

1——E0=0 V/m；2——E0=15 000 V/m；3——E0=30 000 V/m图4 初始速度(vx，vy，vz)=(-1.34×105 m/s，-6.7×104 m/s，-6.7×104 m/s)时氘离子运动轨迹在小环方向上的投影(a)及速度合成(b)Fig.4 Projection of poloidal cross-section of deuterium ion orbit (a) and velocity compose (b) under initial velocity (vx, vy, vz)=(-1.34×105 m/s, -6.7×104 m/s, -6.7×104 m/s)

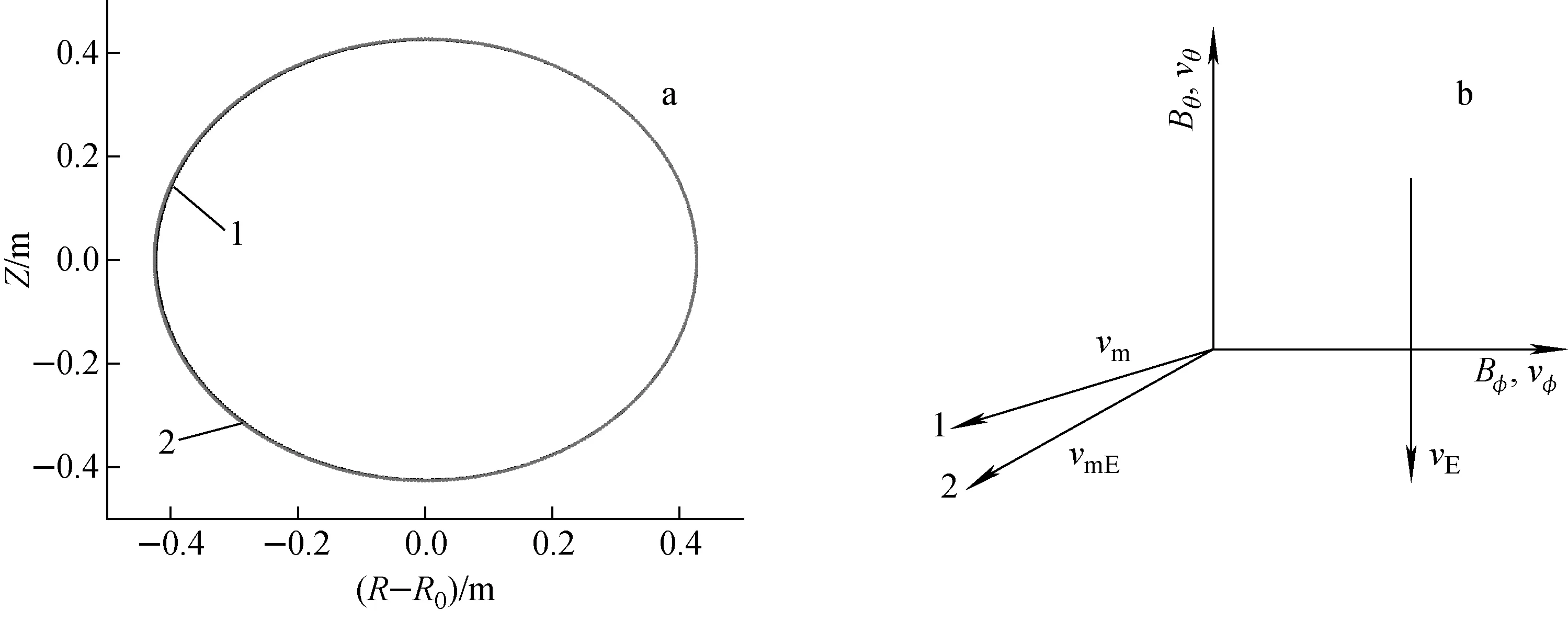
1——E0=0 V/m；2——E0=15 000 V/m图5 初始速度(vx，vy，vz)=(0，-1.65×105 m/s，0)时氘离子运动轨迹在小环方向上的投影(a)及速度合成(b)Fig.5 Projection of poloidal cross-section of deuterium ion orbit (a) and velocity compose (b) under initial velocity (vx, vy, vz)=(0, -1.65×105 m/s, 0)

(10)

其中：f(v)为单位速率区间内粒子出现的概率；k为玻耳兹曼常数；T为氘离子对应位置处平均等离子体的温度。

用蒙特卡罗方法对粒子速度进行抽样，获得整体上满足麦克斯韦分布的100 000个粒子速度样本，然后跟踪每个粒子的运动轨迹，统计俘获粒子的个数，得到粒子俘获率。

图6示出不同初始速度及不同负径向电场下的氘离子俘获率。图6中初始位置(x0，y0，z0)=(2.227 5 m，0，0)。对比相同初始速度、不同负径向电场下的氘离子俘获率可看出：随负径向电场的增大，离子的俘获率逐渐降低，当负径向电场很大时，俘获率很低，基本都是通行轨迹。对比不同初始速度下负径向电场引起的氘离子俘获率可看出：初始速度小时，负径向电场增加引起的氘离子俘获率的变化大。这是因为初始速度小时，沿磁力线方向的速度vm小，在负径向电场不变的情况下，电漂移速度不变，合成速度的相对变化大，所以俘获率变化大。另外，对比负径向电场为0处的俘获率可看出，平均温度为0.46 keV的氘离子的俘获率略低于0.3 keV的氘离子。这是因为能量越高，粒子在边界损失率越高。另一方面，损失粒子占的份额小，所以在图6中显示出略低的趋势。

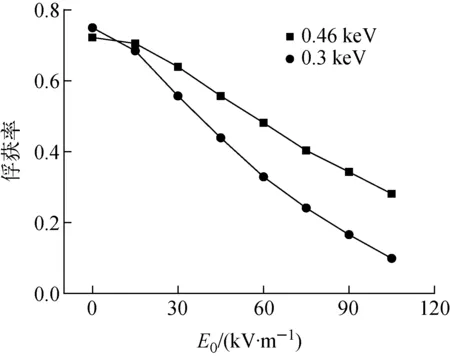
图6 不同初始速度、不同负径向电场下的氘离子俘获率Fig.6 Capture rate of deuterium ion in different initial velocities and different negative radial electric fields

3 结论

根据给定的总电流、中心电流密度、中心密度温度和边缘密度温度等实验参数求解Grad-Shafranov方程，得到了EAST典型放电实验(炮号33068)的平衡位形。结合粒子运动方程得到了考虑负径向电场情况下氘离子在该平衡位形中的运动轨迹，统计了不同初始速度、不同负径向电场的俘获率。模拟结果表明：随负径向电场的增大，氘离子轨迹由扩张轨迹向外翻香蕉轨迹再向内翻香蕉轨迹，最后向压缩轨迹演变；氘离子俘获率随负径向电场的增大而减小，氘离子初始速度越小，其变化越大。