AVMD-KELM方法在水闸结构振动趋势预测中的应用*
张建伟, 华薇薇, 侯 鸽, 赵 瑜, 郭西方
(1.华北水利水电大学水利学院 郑州,450046) (2.水资源高效利用与保障工程河南省协同创新中心 郑州,450046) (3.河南省水工结构安全工程技术研究中心 郑州,450046) (4.河南中原黄河工程有限公司 新乡,453000)
引 言
作为一种低水头的泄流结构,水闸起着至关重要的作用,如水资源利用及蓄水灌溉等方面[1-2]。水闸的流激振动系统是由结构与水体组成的流固耦合系统,其振动形式和机理比较复杂,实际工程中水流形态多变,建筑物形状多样,导致耦合系统的研究更加繁杂,无统一适用标准[3]。许多水闸由于自身特性的原因,长时间处于动静悬殊以及泄流与不泄流交替的特殊环境中,容易发生破坏[4]。为降低失事危险,提高水闸结构的运行效益,采用有效的方法利用有限的数据全面掌握水闸结构振动趋势值得重点关注[5]。
VMD是由Dragomiretskiy等[6]提出的适用于多分量信号自适应分解的一种新方法。该方法的关键是求取最优解,经过迭代循环得到多个IMFs。VMD的分解过程能有效抑制模态混叠,收敛速度快,具有较高的鲁棒性[7]。VMD对实测信号分解时,K值的选取对结果的精确性有极大影响,若K值大于信号分解得到有用成分的个数,则会产生信息叠加的情况;若K值小于信号分解得到有用成分的个数,会导致部分有限带宽的固态模量不能被分解出来。因此,模态总数K的选取至关重要。笔者利用互信息准则确定分解模态数K,减少人为因素的影响。KELM是一种新型的单隐含层前馈神经网络学习算法[8],其隐藏层不需要人为设定并利用最小二乘法进行计算输出权值。该算法不需要人工调节隐含层参数,优于传统的神经网络,收敛速度快,极大减少样本训练时间且误差较小[9]。
基于上述分析,笔者提出一种自适应的变分模态分解算法,并将其与KELM方法结合,建立AVMD-KELM模型对水闸的振动趋势进行预测,以便准确掌握水闸的运行状况,避免不安全的隐患,及时采取防范措施,提高水闸振动的安全水平。
1 基本原理
1.1 变分模态分解
VMD的核心包括变分约束问题与迭代求最优解两部分。本质上,VMD采用变分约束将信号f(t)分解,得到K个模态函数mk(t),使各个IMF分量的带宽最小,且K个IMF分量相加结果为原信号f(t)。变分约束模型[10]表示为
(1)
其中:{mk}={m1,m2,…,mk}表示分解后K个IMF分量。
为得到最优解,引用拓展的Lagrange表达式
L(mk,wk,λ)=
(2)
其中:λ(t)为拉格朗日乘子;〈·〉表示内积运算。
采用对偶分解和交替方向乘子算法[11]解决上述变分问题,不断迭代更新mk,wk与λ(t),求取式(2)的鞍点,即为式(1)的最优解。模态分量函数mk和中心频率wk如式(3)和式(4)所示
1.2 自适应的变分模态分解
采用VMD分解f(t)之前,需要预设分解模态数K,其预设值对分解结果有直接的影响[12]。不同结构的振动特性不同,使得K值难以确定。因此,采用互信息法自适应地选择K值,确保信号分解过程的合理性。
互信息(mutual information, 简称MI)能定量反映两个随机变量间的彼此关联性,更好地衡量两变量的相关水平[13]。互信息表示如下
I(X,Y)=H(Y)-H(Y|X)
(5)
其中:H(Y)为Y的熵;H(Y|X)为条件熵。
当I(X,Y)=0时,X与Y相互独立。Y表示原始信号,X表示分解后的IMF。利用式(6)归一化计算,进而判断原信号是否完全被分解
(6)
当σi低于σ=0.02时[13],表示IMF分量和原信号几乎不相关,认为原信号中的有效成分全部被分解,此时结束运算。
1.3 核极限学习机
Huang等[14]说明了原始的ELM算法,与传统的神经网络算法相比,ELM计算过程简单快速且泛化能力强。因为初始化设定ELM的隐含层参数及权值输入的随机性,使预测结果不稳定。为此,Huang等[15]用核函数代替随机选取的映射,在ELM算法中融入核学习原理,从而提出了新的学习机算法即核极限学习机,该方法的收敛性强,计算速度优于SVM算法。KELM问题表述如下:任意设置隐藏层节点数L,隐藏层的输出函数为
h(x)=[h1(x),h2(x),…,hL(x)]
(7)
输出的权值为

(8)
输入的训练样本为
N={(xi,ti)|xi∈Rd,ti∈Rm,i=1,2,…,N}
(9)
由标准化理论可得KELM的训练函数为
(10)

由库恩-塔克(Karush-Kuhn-Tucher, 简称KKT)原理将式(10)等价为拉格朗日求解最值的问题
(11)
极限学习机的输出函数为
(12)
其中:A为输出矩阵。
在此引入核函数,利用核函数点乘来求解,避免了样本数据在低维空间无法映射到高维度求解的问题。
ΩELM=HHT:ΩELMi,j=h(xi)h(xj)=K(xi,xj)
(13)
(14)
(15)
输出方程为
(16)
选取高斯径向基核函数作为KELM中的核函数
K(x,z)=exp(-γ‖x-z‖2)
(17)
此时,KELM的关键在于对参数C和γ的寻优问题,采用粒子群优化(particle swarm optimization, 简称PSO)算法[16]对参数进行寻优,避免人工选取参数的缺点,使预测结果更加精确。PSO算法的重点是分别运用速度公式vid(t+1)=wvid(t)+c1r1(pid-xid(t))+c2r2(pgd-xid(t))、位置公式xid(t+1)=xid(t)+vid(t+1)得到粒子新的速度及位置。其中:w为权重参数,一般从0.9到0.4递减;c1,c2为学习因子,一般c1=c2=2。
通过PSO对KELM中的C和γ参数进行寻优,利用式(18)求出最佳的一组参数,并将最优参数代入式(16)和式(17),即为最终的模型公式
(18)

2 AVMD-KELM预测模型
为得到水闸结构振动信号更精确的预测结果,采用AVMD将原始信号分解,建立AVMD-KELM预测模型,关键步骤如下:
1) 根据原始观测数据,利用AVMD方法处理原始信号,依据互信息准则确定分解模态数K,并将信号f(t)分解为K个IMF分量;
2) 构建各IMF对应的KELM模型,选取各IMF数据作为模型的训练集和预测集,对各IMF分量进行训练预测;
3) 将水闸中各测点对应的IMFs预测值相加重构,即为最终水闸各测点振动的预测结果。
3 工程实例
于曹闸工程是河南省安阳市区的一座景观节制闸。考虑闸型选择与周边环境协调,加之运行管理方面的安全性能,选取闸孔为7孔且单孔宽为10 m的双扉门闸。蓄水过程中,一扉闸门用来调节最低水位,另一扉闸门控制蓄水高度,在闸门顶部可溢流,泄洪时两扉闸门全部开启。
3.1 拾振器的布置及振动数据的选取
选取节制闸4#孔的闸墩及工作桥为分析对象,在闸墩两侧的水平向各布置4个测点,右侧闸墩顶部处为4号测点,1,2和3号点均匀布置于右侧闸墩上部,相距约3 m;8号点布置在左侧闸墩顶部,5,6和7号点均匀布置于左侧闸墩上部,相距约3 m,且两闸墩的测点相互对称。竖直向共有3个测点布置于工作桥面,3个传感器测点均匀布置于工作桥面,9,10和11号测点相距约1 m,具体位置如图1所示。原型观测对象工况为4#孔右侧的3#闸孔始终处于关闭不过流状态, 左侧5#闸孔始终处于开启过流状态, 采样时间为10 min, 采样频率为100 Hz。信号监测中11个测点同时采样, 完整记录闸门从开始到关闭的全过程。

图1 传感器布置示意图Fig.1 Schematic diagram of sensor layout
闸门原型观测采用DASP振动测试系统采集数据,该系统如图2所示。原型观测试验传感器是中国地震工程力学研究所研制的INV9822型加速度传感器,频响范围为0.5~4 000 Hz,灵敏度为200 mV/g。现场部分测点采集系统如图3所示。

图2 DASP振动响应测试框图Fig.2 Block diagram of DASP vibration response test

图3 闸墩部分传感器布置Fig.3 Partial sensor layout of pier
闸门的左右闸墩为对称结构,且测点均匀对称分布,本次预测选取测点2,5,7,9为分析对象。振动监测数据共4组,为使预测结果更加全面准确,每100个数据点选取50个,每组各取4 096个数据点,前3 000个为训练样本数据,余下1 096个为预测数据。以5号测点为例,监测数据的振动情况如图4所示(为了更加直观地观察结构振动趋势,振幅图每隔25个时间间隔取点画图,取前160组数据)。
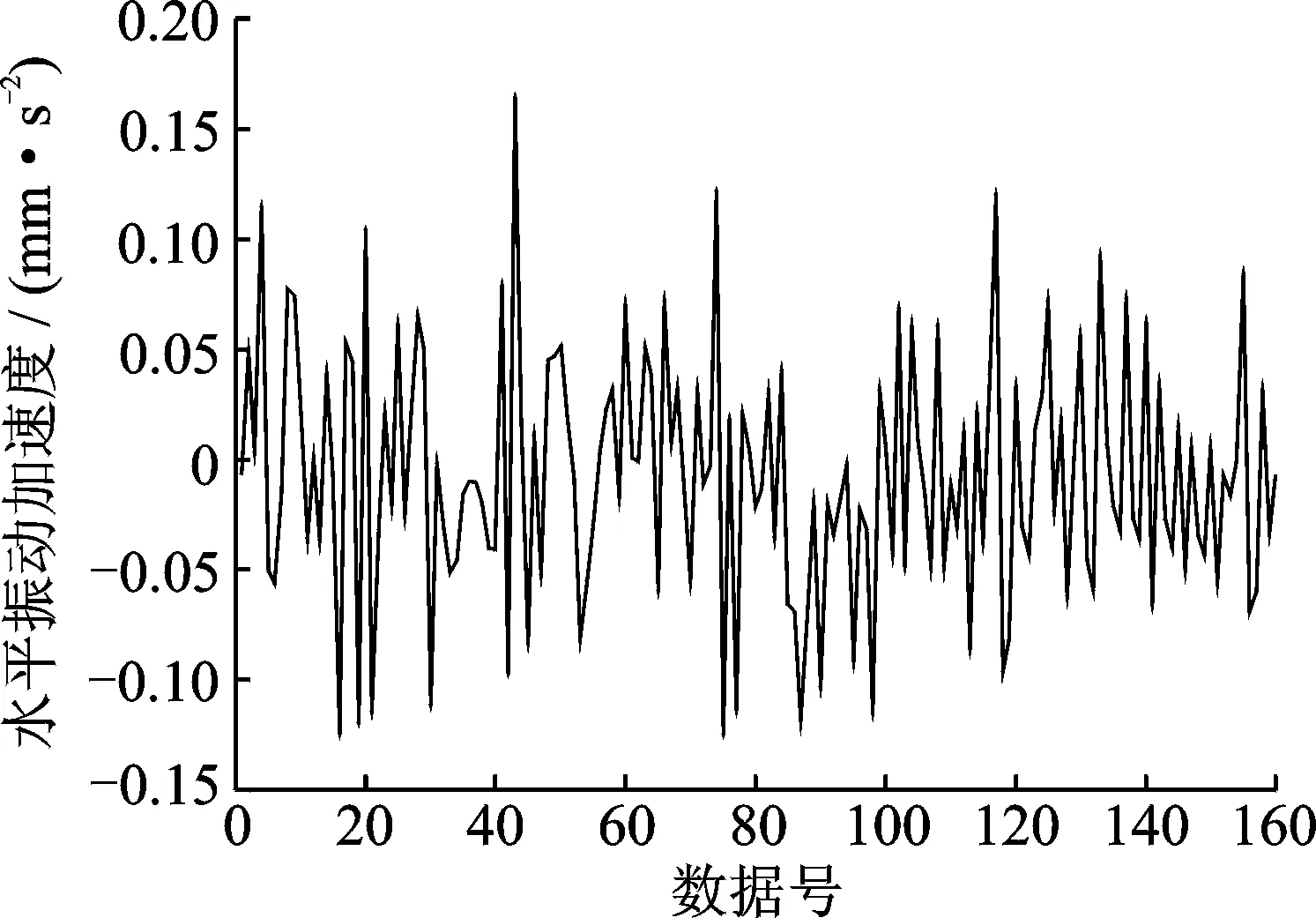
图4 5号测点振动监测数据Fig.4 Vibration monitoring data at point 5
3.2 AVMD分解结果

图5 5号测点振动数据AVMD分解结果Fig.5 AVMD decomposition result of vibration data of point 5
以5号测点为例,对其进行AVMD分解,利用互信息法确定出分解的模态数K=4,分解得到的4个IMF分量如图5所示。由图5可以看出,AVMD将原始序列分解为波动速率不同的4个分量,其中m4波动速率最快,m3次之,m1波动速率最慢。各个IMF分量与原给定振动序列的归一化互信息值见表1,由表1可知,测点的4个分量归一化值均大于阈值σ=0.02时,满足分解要求。
表1 5号测点IMF归一化互信息值
Tab.1 The IMF normalized the mutual information value of 5 point

IMF1IMF2IMF3IMF41.000 00.042 30.047 10.627 0
3.3 AVMD-KELM模型预测结果及对比
采用KELM模型对AVMD分解得到的各IMF分量进行预测分析,并将各测点对应的预测值相加重构,获得各测点预测结果。为验证AVMD-KELM模型的有效性,将其分析结果与KELM模型、SVM模型相比并进行分析,其中KELM模型和SVM模型直接对水闸的原始振动序列进行预测。为了保证对比结果的准确性和有效性,3种预测模型中的核函数均为高斯径向基核函数,模型中的参数均采用PSO优化,其预测值与实测值比较结果如图6所示。
由图6可知,3种模型的振动预测结果与实测信号的吻合程度均在可接受范围内,且在预测过程中,KELM模型预测速度比SVM模型更快。为了更加科学客观地对预测结果进行分析,如表2所示,笔者引用均方根误差 (root mean squared error, 简称RMSE)和平均相对误差(mean relative error,简称MRE)两种评价指标对模型预测结果进行定量分析[16]。

图6 各实验测点实测数据和预测结果对比图Fig.6 Comparison between the measured data and the predicted results of each test point
表2 3种模型预测结果的RMSE与MRE指标值对比
Tab.2 Comparison of RMSE and MRE index values of three model prediction results

测点RMSEMRE/%AVMD-KELMKELMSVMAVMD-KELMKELMSVM20.1050.3130.2987.112.111.950.1750.2590.3047.811.512.070.2720.6350.6818.319.220.390.3180.6610.7139.620.321.6
RMSE与MRE值越小,表明预测效果越好。从表2的对比结果可以看出,AVMD-KELM模型预测的RMSE与MRE结果均小于KELM和SVM预测模型,AVMD-KELM预测结果的MRE均控制在10%以内,整体预测数据和实际数据误差在接受范围之内。这表明本研究方法适用于水闸结构振动预测,且工程实用性更强。
4 结 论
1) 基于AVMD-KELM模型得到各测点的预测值与实测值较为吻合,RMSE最大为0.318,MRE最大为9.6%。与KELM和SVM预测模型对比分析,AVMD-KELM模型对水闸振动趋势的预测较为理想。
2) 利用互信息法定量来确定K值大小,并采用AVMD算法将水闸结构振动信号较好地分离成K个IMF分量。KELM利用最小二乘法可直接求出输出层所需要的权值,节省大量的训练样本时间,具有强大的泛化性能。在预测过程中,KELM模型比SVM模型的预测速度快。与单一的KELM模型相比,AVMD-KELM预测模型大幅度降低了振动信号复杂因素的干扰,各IMF分量能更好地反映水闸结构的振动情况,提高了水闸结构运行的安全水平。

