不同类型复杂网络中个体合作行为互动的演化博弈模拟

章 平，黄傲霜，罗宏维

(深圳大学中国经济特区研究中心，广东 深圳 518060)

0 引言

人类社会和生物界中普遍存在着合作行为，合作被视为人类社会的基本问题之一。“合作行为是如何演化的”是美国《科学》杂志提出的125个重大科学前沿问题之一。这一问题，也始终是经济学及相关学科关注的根本问题之一。

第二，社会偏好与自利偏好同时存在。经典博弈论假设参与者严格按照利益最大化原则进行决策，而行为博弈论的发展表明人们并非会严格的计算利益得失，而是普遍存在着互惠、利他、公平等社会偏好。在看到人的自利、机会主义的搭便车行为的同时，大量的实验室实验和田野调查表明，人们并非完全自利者，关注他人、追求公平的社会偏好普遍存在。在Guth开始的最后通牒博弈实验中，提议者会平均分配给响应者30%到50%之间的初始禀赋，当分配额小于20%时，大约一半的响应者会拒绝[6]。Forsythe等首先主持的独裁者博弈实验[7]、Gerald Marwell等开创的公共品博弈实验都说明人们对利他、互惠和公平的关注[8]。

第三，如何从内在动机激发合作行为。在承认人的自利和利他两种偏好共存的前提下，研究开始更全面地考虑如何才能促进合作行为的发生[9]。人的行为不仅仅受到物质激励的驱动，还会受到决策环境因素、伦理道德规范、实验设计、个体异质性(如职业、性别、年龄等)、初始禀赋等因素的影响。这使得人们对实验室结果产生了质疑，并进而推动了田野实验的发展——利用更接近现实状态的决策环境研究如何激发合作行为[10]。

首先，开展基于行为设计的田野实验研究如何激发合作。Akerlof和Yellen所研究的“礼物馈赠行为”体现了人们互惠的行为模型[11]。Fehr在此基础上设计了礼物交换实验并得到了同样的结论[12]。同样运用礼物交换实验框架，研究者在中国南方的一家工厂设计并进行了一项田野实验，实验结果再次印证了“礼物交换”中互惠的社会偏好[13]。相反，当人们感受到不公平时，会表现出不合作的情况：美国新泽西州的警官们的待遇在20年内没有得到应有的增加时，劳动仲裁结束后，犯罪报告增加、而逮捕率降低了[14]。

本文思路取材于Nowak的空间博弈理论。Nowak率先将演化博弈理论与规则网格网络结构结合，研究了空间中的群体演化博弈行为[22]，使得空间博弈得到了广泛的关注。Nowak提出了合作的五大机制：亲缘选择、直接互惠、间接互惠、空间博弈和群体选择[23]。

人类生存的社会是个巨型社会网络，由于社会网络的复杂性、人群的异质性、交互规则的多样性，研究合作行为的传统方法面临着巨大的考验。而基于场景和人群分析的基于行动主体的建模(ABM,Agent Based Model)方法突破了传统研究方法在此方面的窠臼，通过科学的建模技术以及严谨的检验，为研究合作的产生提供新的研究思路。

充分考虑到上述研究进展和改善空间，在本文余下部分，将在NetLogo仿真平台上采用ABM方法设计仿真实验，研究规则格子网络、无标度网络和小世界网络3种典型社会网络拓扑结构下合作的演化，比较何种网络更有利于合作的发生，并探讨如何设计有效的激励机制以维持和促进合作。

1 演化博弈模型与互动规则

1.1 基础模型构建

研究不同网络结构中的合作演化，假设每个个体在每个时钟周期都和其邻居进行一轮公共品博弈，这里的邻居就是个体博弈的对象，与搭载博弈群体的社会网络结构相关。模型中搭载博弈群体的拓扑结构有3种：规则格子网络、BA无标度网络以及WS小世界网络。

每轮博弈中，都没有一个中央领导者控制，个体都有两个选择：合作或背叛。个体具体会选择哪种策略，和一系列因素相关，这也是实验会考察的方面。而其策略都会对邻近的主体产生影响，采取合作策略会产生正外部性，其他主体会因此获益。外部性体现了主体与相邻主体互动的社会能力。

我们希望通过实验，寻找合作发生的机理——具体和哪些因素相关，多轮博弈后最终能否得到稳定的演化结果？实验中还会因地制宜地引入激励机制，以推动原本的演化结果由背叛转向合作。模型中的每个主体都由4个要素描述：1)本轮的策略是合作还是背叛；2)上一轮的策略是合作还是背叛；3)本轮得分；4)为了便于在仿真过程中观察结果，主体还被赋予不同的颜色以作区分。在邻居的选取方面，在小世界网络和无标度网络中，选择其邻居节点为其博弈对象；对规则格子网络，采用了冯·诺依曼型(4个邻居)及摩尔型(8个邻居)两种邻居选择方式。

表1 颜色及其代表的含义Tab.1 Colors and representative meanings

1.2 交互与策略转换规则

演化博弈中最重要的部分是个体之间的交互(interact)和下一轮策略的选取(strategy select)阶段。假设所有的个体都是同质的，有相同的策略集。

当个体采取合作策略时，其获得的净收益为合作收益R减去合作成本C，为了研究问题的方便，令收益R为其所有邻居节点的总数加上1(也就是它自身)，合作成本为1，也就是每个节点的净收益就是total-num-of-cooperation-neighbors，即其邻居节点的总数。

当节点选择背叛策略时，背叛者会得到一定的收益，同时由于邻居节点的合作，背叛者会搭便车，享受到邻居节点的正外部收益，所以其收益是背叛激励乘以其邻居节点中合作者的总数，即defection-award * total-num-of-cooperation-neighbors。

因此，对于每个个体，都去统计其邻居节点中合作者的数量，而如果个体是合作者，其分数就是其邻居节点中合作者的总数；如果个体是背叛者，其分数是背叛收益与合作者邻居总数之积。本文中，我们主要采取选择邻居节点中得分最高者的策略作为自身下一轮的策略，刻画演化博弈中向强者学习的特征。

激励政策在此被细化为奖励(或补贴)r(reward)和惩罚p(punishment)。激励政策将对合作者给予奖励为唯一策略，或将对背叛者给予惩罚为唯一策略。主体会对外界的刺激作出反应，即会考量中央给予的奖励或处罚再做决策。模型会比较无政策、奖励政策、惩罚政策3种情况下，哪种会取得最优的结果(最优结果由合作者的个数来决定)，以确定最优方案。当模型中引入奖励机制时，对应于现实中对合作者的奖励，此时引入了奖励reward，合作者的效用函数中会增加奖励，即total-num-of-cooperation-neighbors+reward，采取背叛策略的主体的效用函数不变。当模型中引入惩罚机制时，对应于现实中对背叛者的惩罚此时引入了惩罚punishment，背叛者的效用函数中会减少一个值p，即defection-award * total-num-of-cooperation-neighbors-punishment，采取合作策略的主体效用函数不变。

预期结果与初始合作者的个数、群体规模，背叛收益大小、网络拓扑结构相关。然后有针对性地改进参数设置，施加激励、预期奖励的大小、惩罚的大小也会影响最终演化结果。

1.3 网络规模、初始合作概率、背叛收益和激励机制参数设置

模型中的参数有4个。1)num-nodes：表示网络中节点总数，也就是博弈群体的规模，取值范围根据不同的网络略有不同；2)initial-cooperation：表示初始合作概率，取值范围在0～100%之间；3)defection-award：表示背叛收益，取值范围为0～10之间；4)施加激励机制的模型中还会有reward和punishment参数。表2展示了实验的参数和其取值范围。

表2 实验参数及取值范围Tab.2 Experimental parameters and value ranges

1.4 仿真模拟分析

依据上一部分模型的构建进行仿真模拟。模型采用模块化设计，包含两个模块：网络结构构建模块和演化博弈模块。原理如下：首先，建立特定拓扑结构的网络；然后进行初始化，即按照初始合作概率initial-cooperation令群体中一部分行为主体(在网络中用节点表示)初始化为合作策略，用蓝色标记；另一部分行为主体采取背叛策略，用红色标记。需要注意的是，我们的初始化过程采用生成随机数的方式，random-float 1.0<(initial-cooperation/100)，即随机产生一个小于1的正浮点数，如果该浮点数小于初始合作概率，就令个体采用合作策略，所以并不是绝对意义上的initial-cooperation比率的合作者。基本上是服从正态分布的，所以并不影响我们的实验结果。接下来的演化中，根据行为主体选择的策略改变其颜色。

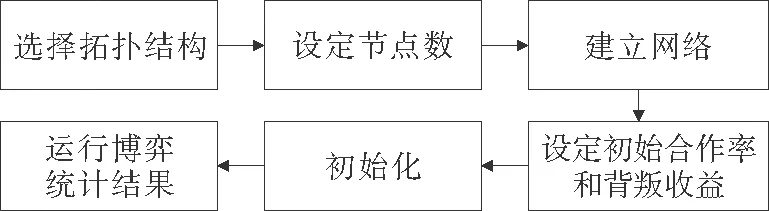
图1 实验流程示意Fig.1 Experimental flow diagram

当所有的主体都变成背叛者或者合作者时，或者所有主体的策略都不再变化时，停止演化程序的进行。当实验设定原始节点都是合作或者都是背叛的时候，显然，只需0步就达到演化稳定状态，因为个体无法学习新策略，其邻居节点是相同的。图1是实验流程示意图。

2 规则网络下的合作行为演化

2.1 背叛收益对演化结果的影响

实验使用了NetLogo自带的行为空间，参数为：网络规模大小25^2=625个节点，背叛收益从0.1增加到0.9，增加量0.1，初始合作概率从1增加到100，每轮增加1。每个实验都进行5次，仿真时间为500个时钟停止。实验进行了4 500次，结果是无一例外的个体全部演化为合作。

图2 仿真状态的初始化、中间状态和结果状态

实验发现，不管如何去改变初始合作概率，哪怕其值非常小，合作仍可入侵这个群体，因为背叛的收益小于合作收益，所以这个群体最终会演化为合作群体。

当增加背叛收益值：令其取值为1.1、1.2、1.3三个数时，演化会出现有2个点为背叛的情况。进行1 485轮，得到的结果有两种：全部合作或有少量背叛点的稳定状态。

出现这种演化结果要从设定的效用函数出发。每一轮节点都从表现最好的邻居状态中选择自己下一轮的策略，而每个个体的得分来自于周围邻居节点的合作者的个数。图2中红色节点的得分为3*(1.1，1.2，1.3)=(3.3，3.6，3.9)，与其相邻的蓝色节点的得分均为3，但是不与红色节点连接的点的得分为4，所以无论是红色节点还是蓝色节点都没有动力去改变现状。由于实验中背叛收益参数的设置按照0.1递增，可以推测如果设置为按照0.01递增，则只要defection-award取值在(1，4/3)之间，都会有这种情况出现，总之这是效用函数的设置引发的结果。继续增加背叛收益值，令其取值为[1.4,2.9]时，会出现演化无法达到均衡的情况(超过40万轮)。图3分别是演化的初始状况和不同的阶段。而当背叛收益大于等于3时，不管其他参数的设置，背叛策略都有绝对的优势。

表3中，[1 1 99]的表达方法沿袭了NetLogo中行为空间的表示方法，左右分别表示初值和终值，中间的1是递增量，也就是取值从1每次递增1到99为止，即取值范围是1,2,3,…98,99。

图3 背叛收益取值在初始状况及演化的不同阶段

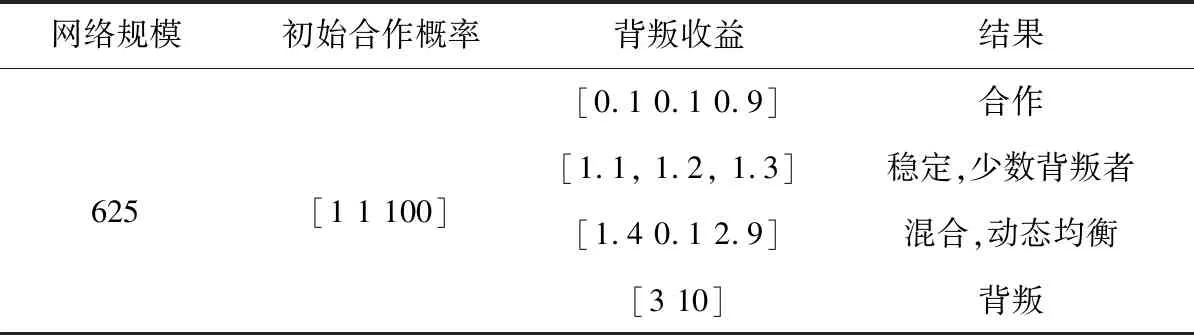
表3 不同背叛收益下的演化结果

2.2 初始合作概率对演化结果的影响

接下来的实验，我们在不同的背叛收益下不断改变初始合作概率，观察结果。当背叛收益较高的情况下(defection-award≥3)，无论初始合作概率多高，最终的结果都是背叛。初始合作概率从1递增至99，背叛收益从3递增至10，每个实验进行5次，共进行3 960次实验，都得到背叛的结果。

当把背叛收益设置在(1.3,3)之间时，无论如何去改变合作率，都很难达到演化均衡状态，双方的博弈势均力敌，任何一方没有谁会绝对占据优势。实验中令初始合作概率从1递增至99，背叛收益从1.4递增至2.9，实验进行7 920次。两者都势均力敌，但是谁最终都难占据绝对优势。

当固定背叛收益为1.9时，令初始合作概率从1递增至99，随着初始合作概率的增加，最终群体中合作者的比率并没有明显变化。所以我们认为，在当前效用函数设置下，初始合作概率的大小并不会影响演化结果及演化速度。

2.3 扩大邻居数量对演化结果的影响

本轮实验为每个个体扩展了邻居的个数，从冯·诺伊曼型邻居扩展到摩尔型邻居，此时增加了博弈邻居的个数。

表4 参数设置及结果

背叛收益取值1.1或1.2时，演化结果可能是合作、背叛、少数背叛者的稳定状态，都有可能发生。当背叛收益为1.3时，合作、背叛或者少量背叛者的稳定以及混合状态都会出现，初始合作概率较大时，容易演化为以合作者为主的群体；初始合作概率较小时，容易演化为以背叛者为主的群体。这几种情形下，演化结果都与初始合作率相关。

当背叛收益在[1.4,1.6]范围时，若初始合作概率小于25%，容易出现演化稳定的结果，不容易出现势均力敌的混合状态。

实验发现，当扩大了博弈的邻居范围时，更容易演化为背叛，此时只需要较小的背叛收益，就可能演化为背叛群体。这是因为行为主体博弈得分和邻居节点的个数相关。

2.4 改变策略对演化结果的影响

最后在实验中改变演化策略，把自身的策略加入与邻居策略对比，发现这种情况下演化的速度大大提升，很快就会达到均衡，而且很容易导致背叛的结果，在背叛收益为2时，所有个体都演化为了背叛。因为这种策略选择方法是更有效率的方法。不光模仿邻居，也将邻居的策略与自身比较，如果自身的策略好，就保持自身策略不变。

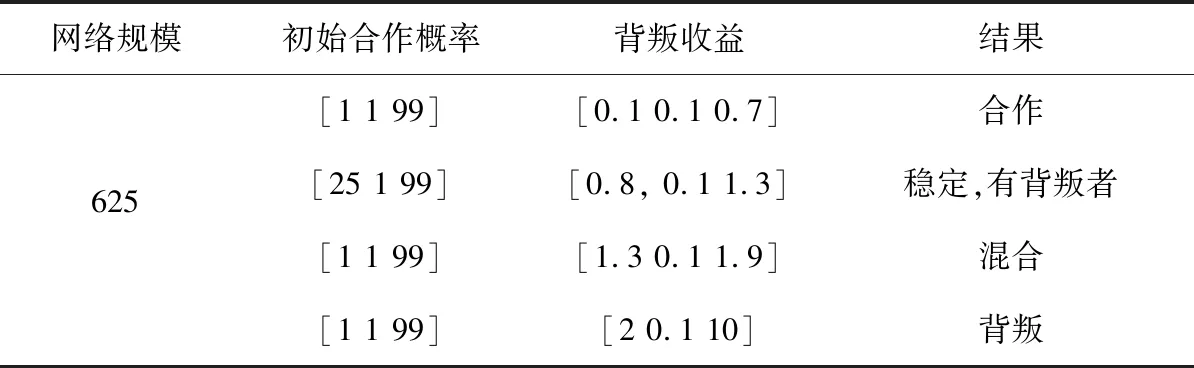
表5 参数设置及结果

另外，当背叛收益取值在0.8和1.3之间时，实验中还出现了如图4所示的稳定状态，背叛和合作共存且都无改变自身状态的动力，在实验三中已经分析了其缘由。图4从左到右依次反映了随着背叛收益的增加，稳定状态中背叛者的比率也不断升高。

图4 稳定状态

2.5 规则网络仿真模拟结果

1)当背叛收益小于合作收益时，不管如何去改变初始合作概率，哪怕初始合作概率非常小，合作仍可入侵，所以这个群体最终会演化为一个合作的群体。当背叛收益较高的情况下(defection-award≥3)，无论初始合作概率多高，最终的结果都是背叛。在当前效用函数设置下，初始合作概率的大小既不会影响演化结果也没有影响演化速度。背叛收益在1.4至2.9之间时，会出现势均力敌的情形，两种策略都无法达到演化均衡状态；背叛收益取值在[1.1,1.3]时，会出现有少量背叛点的稳定状态。

2)当前设置下，初始合作概率不会影响演化结果。

3)当扩大博弈的邻居范围时，更容易演化为背叛，此时只需要较小的背叛收益，就可能演化为背叛群体。背叛收益取值1.7以上便会演化为背叛，当背叛收益取值1.1、1.2、1.3时，各种演化结果都可能出现，这是与冯·诺伊曼型邻居的不同点。

4)改变演化策略，把自身的策略加入与邻居对比的情况下，演化的速度大大提升，很快就会达到均衡，而且很容易导致背叛的结果，也降低了背叛收益会演化为背叛的值，在其取值为2时就会演化为背叛群体。

表6 参数设置

3 无标度网络中的合作行为演化

3.1 背叛收益对演化结果的影响

当固定网络规模、初始合作概率，改变背叛收益时，发现随着背叛收益的提高，群体会更容易演化为背叛群体。我们的参数设置和结果如表6所示。然后设定较小的初始合作概率为2%，背叛收益设置较高为10，初始节点数为200，进行20次实验，结果如表7。

结果显示，即使背叛收益很大(10倍)，初始合作概率较小(2%)，BA无标度网络结构下，合作还是可能入侵，并最终使得所有个体都演化为合作，只是需要较长的时间，演化为合作状态需要的平均轮数为31.375轮。而演化为背叛状态需要的平均轮数为5.417轮。因此，相对于规则格子网络，BA无标度网络有利于合作的进化。

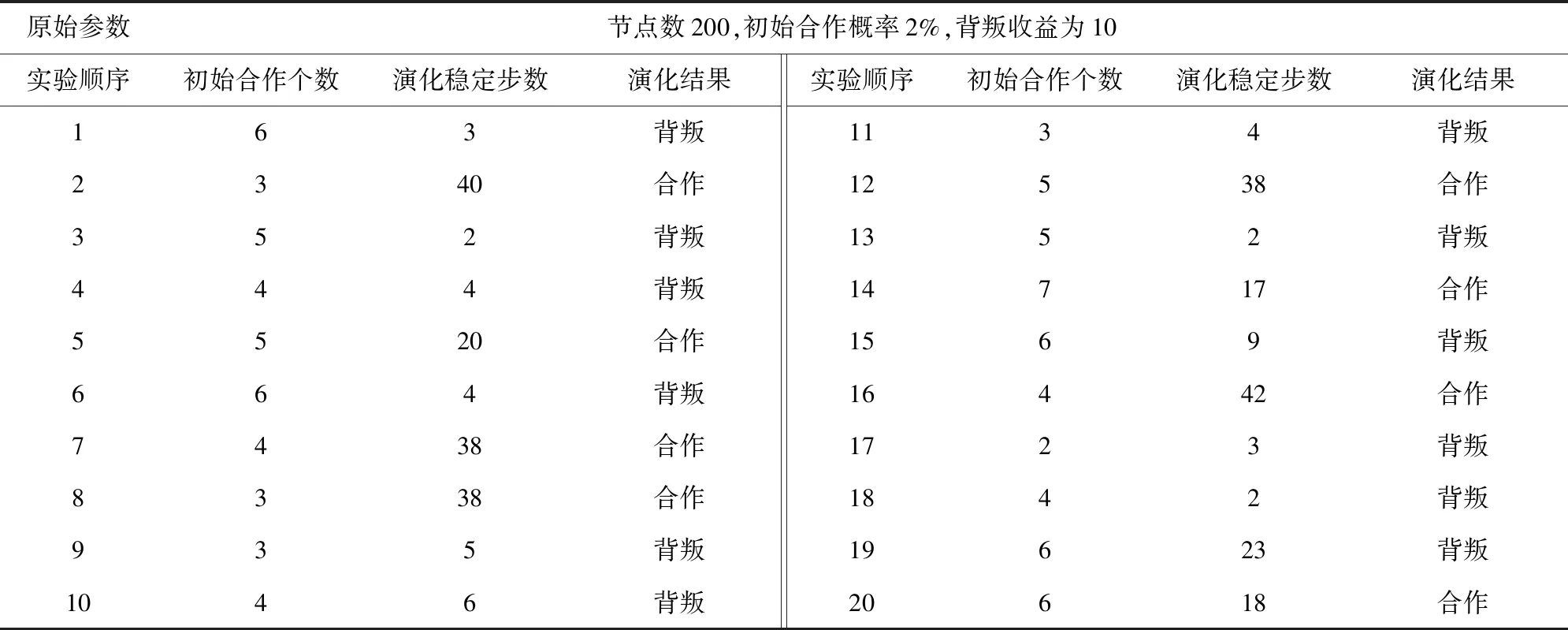
表7 原始数据

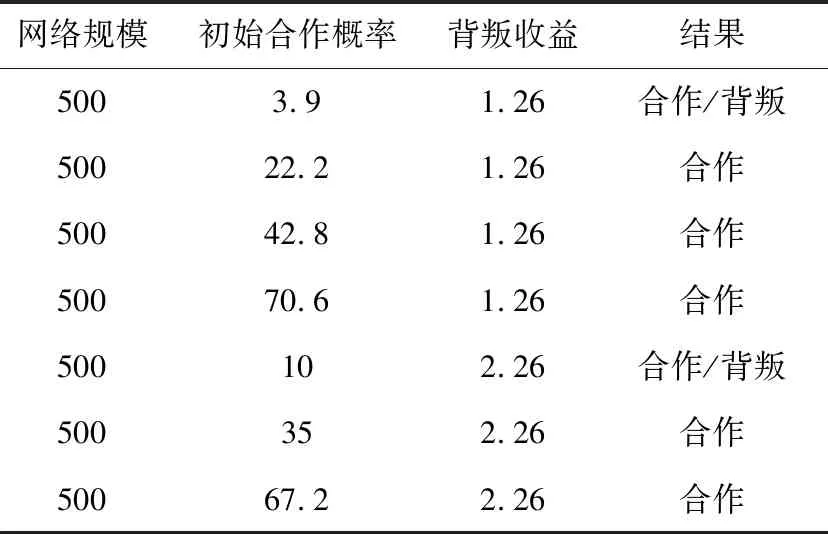
表8 参数设置

3.2 初始合作概率对演化结果的影响

初始合作概率会影响演化结果。如表8所示的参数和结果，当背叛收益较小时，初始合作概率要较大才能保证群体全部演化为合作群体；随着背叛收益的增大，初始合作概率同时也要增大，群体才会全部演化为合作群体。

3.3 个体空间分布对演化结果的影响

无标度网络的一个突出特点是“强者愈强，弱者愈弱”。少数节点的度很大，多数节点的度很小。改变最初随机分配合作点和背叛点，而是指定节点为合作，观察其现象。比较了随机选中19个点以及给定的度数大于5的19个点，发现演化的结果并无较大差异。

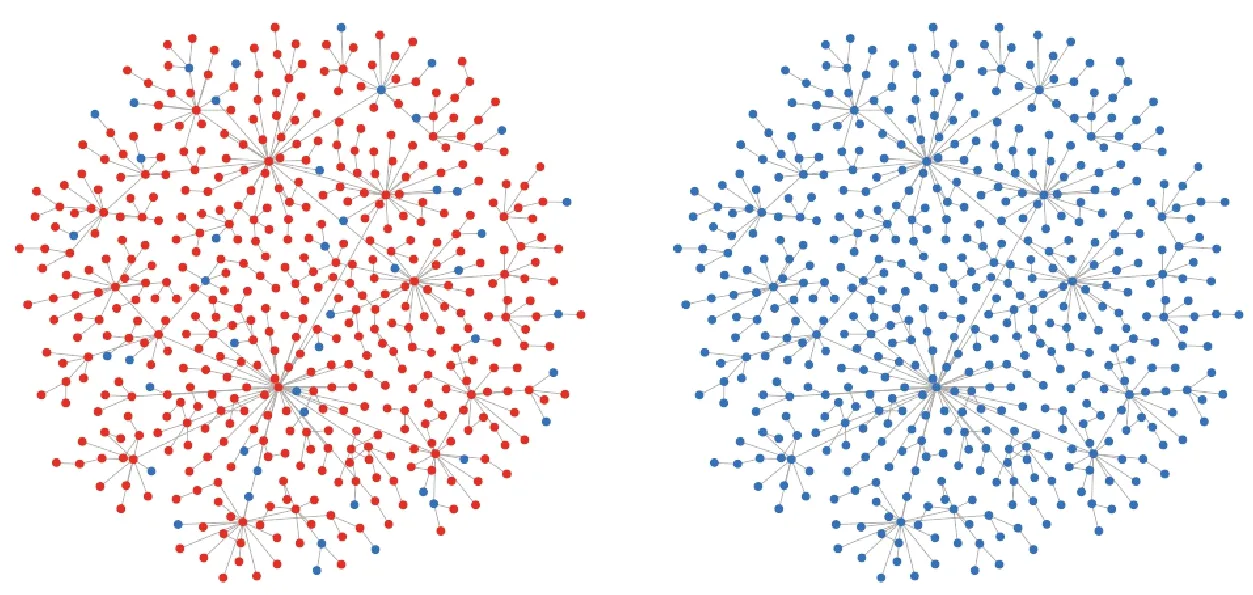
图5 500个节点、10%合作率的博弈结果

当设定总节点数为300时，分别考察指定度数大于3的节点、大于10的节点、大于5的节点为合作者，与随机分配相同数目的节点为合作者，发现在现有的效用函数设定下，指定节点与随机分配几乎不影响最终的演化结果。

3.4 改变策略对演化结果的影响

在本轮实验中，我们设计为：个体不再选择邻近节点中收益最高的策略作为自己下一轮的策略选择，而是将邻近节点的策略收益与自己的策略收益作比较，采用第二种方案与第一种方案进行对比。若自己策略收益高于所有邻近节点，则采取自己的策略；反之，则选择邻近节点中收益最高的策略作为自己下一轮的策略。这一点是和规则网格不同的，规则网格里邻近节点数只有2、3、4三种(或摩尔型的3、5、8)，而BA无标度网络中节点的度数差异很大。当背叛收益小于1时，每轮演化都会到达合作状态。当背叛收益大于1时，最终的演化结果却大不一样。

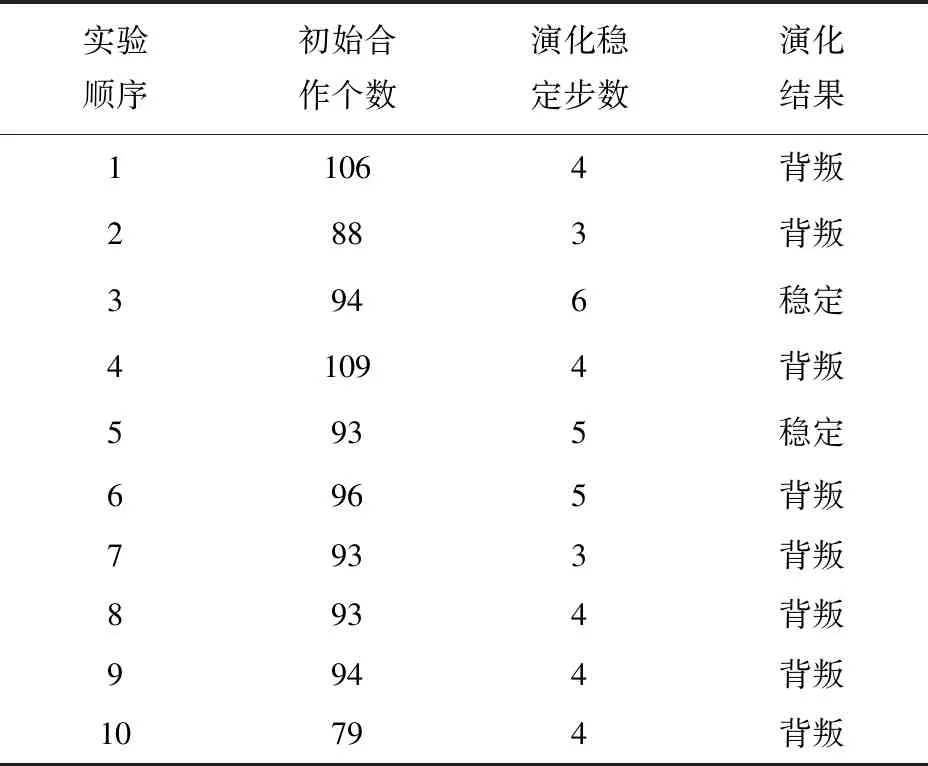
表9 原始数据

注：原始参数：节点数500，初始合作概率20%，背叛收益为2.77

实验进行20次，除了会快速演化为背叛状态——平均5轮博弈，还会出现图6所示的一些稳定状态。达到均衡状态速度的加快是由于每个个体会跟自己现有的状态比较，两种策略的权衡会加快演化速度，最终很快都会到达全部背叛的状态。

而有时由于初始节点状态分布，会导致合作者和背叛者都不再去改变自己的状态，此时自己当前的分数高于所有邻居节点的分数，因此所有的节点都没有动力改变现状，此时合作者会形成一个簇，而如何打破这种稳定状态是个有意思的研究点。

3.5 无标度网络中的合作行为演化模拟结果

与规则格子不同，背叛收益和初始合作概率都会影响演化结果。

1)随着背叛收益的提高，群体会更容易演化为背叛群体。但是即使背叛收益很大(10倍)，初始合作人数较少(2%)，BA无标度网络结构下，合作还是可能入侵，并最终使得所有个体都演化为合作，只是需要较长的时间。

图6 稳定状态

2)同等背叛收益下，当初始合作概率较高时，群体更容易演化为合作群体。

3)在背叛收益较小(如不超过3)的情况下，指定度数较高的节点为合作初始节点，与随机分配相同合作节点进行比较，进行多次实验，指定节点与随机分配并无区别。

4)当改变演化策略时，会出现一些合作者与背叛者共存的稳定状态，此时合作者会形成簇，所有个体都无动力改变现状。

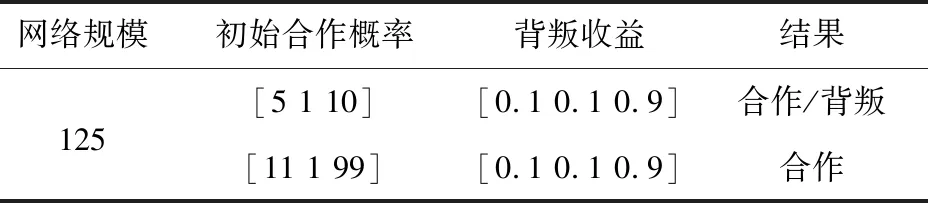
表10 参数设置

4 小世界网络中的合作行为演化

4.1 背叛收益对演化结果的影响

为了便于观察，实验设置节点数为125个。当背叛收益小于1时，只要合作者在一定比率以上，如10%，实验的结果只有一个——全部演化为合作，原因是背叛收益还不如合作收益高，个体自然会选择合作。使用行为空间工具，将初始合作概率从5递增至99，背叛收益从0.1递增至0.9，每个实验进行5次，运行4 275次，有20余次背叛，其余都是合作，且背叛多分布在初始合作概率较小的区间。

由于实验设置节点数较少，当初始合作概率较小时，只有少数的点是合作节点，如只有三五个，群体很可能会演化为背叛群体。因为演化策略的选择仅从邻居节点中的最高得分者中选取，而当合作者太少，合作者无法从合作中获益，不利于群体中其他个体的学习。当初始合作概率取值大于10后，排除偶然因素，全部会演化为合作。图7描绘了演化的三个状态，初始、全背叛、全合作。

图7 演化的3种状态

为了剔除不合理的数据，实验中把初始合作概率从10依次递增至90，改变背叛收益后的结果如表11所示。此时实验设置的参数如下，节点数125，小世界网络随机重连接的概率为0.36。当背叛收益超过2.5时，无论初始合作概率如何增加，都不会影响背叛的结果。

表11 参数设置

实验发现，背叛收益为2左右时，博弈两方相持不下，会进行数万代仿真才能达到背叛的演化均衡(多数结果是背叛)，有时候还未必达到均衡。可以与规则网格中演化无法达到稳定的状态进行比较。双方出现了势均力敌的现象，每一方都很难占据绝对优势。图8展示了博弈模拟进行10 000轮时的状态。

图8 博弈模拟进行10 000轮呈现的状态

当固定节点数为125、初始合作概率为10%时，将背叛收益从4提升至8时，在不断增加背叛收益的过程中，演化稳定所需步数呈现出逐步下降的趋势。

4.2 初始合作概率对演化结果的影响

实验发现，当背叛收益为4时，稳步提升初始合作概率并不能改变结果总是背叛的状态，当继续增加初始合作概率至98%，背叛仍旧可以入侵这个团体。因此，小世界网络和规则格子网络是比较类似的，只要背叛收益高于一定的值，群体就不可能演化为合作群体。

经过不断的实验，得到临界的背叛收益是2.5，即当节点数为125，背叛收益取值大于等于2.5，随机重连接的概率为0.36。此时只能演化为背叛。

表12 参数设置

表12通过对比发现，当背叛收益较小时，提高初始合作概率可以使得结果向着合作方向演化。

4.3 改变平均路径长度对演化结果的影响

小世界网络的一个特征是平均路径长度较短，本次实验通过改变随机重连接的概率以改变平均路径长度。

实验在初始合作概率为50，背叛收益为3，节点数为125，随机重连接概率从0.2递增至0.6的情形下，进行60次实验。虽然最终演化结果没有变化，然而随着随机重连接概率的增加，演化稳定所需要的步数却不断增加。

表13 改变平均路径

表13比较了其他参数一致，平均路径长度不一致的演化稳定步数。

4.4 改变演化策略对演化结果的影响

本次实验个体会将自己的分数与邻居节点进行比较，若高于所有邻居节点就采取自己的方案，否则，就选择邻居节点中得分最高的策略作为自己下一轮的策略。

把自身的策略加入与邻居策略对比，这种情况下演化的速度大大提升，很快就会达到均衡，而且很容易导致背叛的结果，在背叛收益为2时，所有个体都演化为了背叛。

4.5 小世界网络中的合作行为演化模拟结果

1)当背叛收益小于合作收益时，即使很少的合作者也可能入侵背叛群体，并占据绝对优势；背叛收益的提高，会使得演化速度加快，更快到达均衡点。有时会出现合作和背叛势均力敌的情况，会演化上万步都不能达到均衡；背叛收益超过一定值时，结果只能是背叛。

2)在背叛收益相对较小的情况下，提升初始合作概率，会使得群体朝合作演化。但是当背叛收益超过一定的数值，提升初始合作概率并不会改变演化为背叛的结果。

3)当改变平均路径长度时，演化稳定所需要的步数不断增加。

4)和规则网格结构一致，将自身策略加入对比，会加快演化的速度，较小的背叛收益都会导致背叛。

5 结语

论文主要研究复杂网络上的演化博弈，分析了3种典型的网络结构(规则网络、无标度网络、小世界网络)中的群体博弈，选取群体间博弈经典模型——公共品博弈，通过仿真研究网络规模、初始合作概率、背叛收益以及邻居节点选择方式对博弈结果的影响，探讨如何设计有效的激励机制以维持和促进合作。

根据实验结果可以判断：规则格子网络和小世界网络的共性更多，而无标度网络更有利于合作的进化。在规则网络中，初始合作概率不会影响演化结果。与规则网格相比，BA无标度网络更加有利于合作演化，初始合作概率和背叛收益都会影响最终的演化结果。与BA无标度网络对比，小世界网络更不利于合作的演化，即便初始合作概率较高，背叛收益不高的情况下，也很容易出现为全部背叛的状况。这对于我们在设计有效的激励机制以维持和促进合作中具有启发性，即激励和惩罚对个体在博弈中收益大小产生影响，以此促进合作行为的涌现。

此外，论文中尚存有待改善的探索，比如博弈群体规模偏小，博弈轮数也较少，在较少的博弈次数下达成的策略均衡是否具有稳定性等一系列问题都是今后工作需要解决的难点。特别是在未来研究中我们将考虑纳入随机冲击的影响，“随机冲击”在理论和现实中对社会经济系统演化的历史路径和未来预测具有重要影响，尤其是在模型设计和冲击的特征刻画上，我们将在已有文献的基础上进行拓展细化。