新型桥梁泄水管非饱和渗流场分析

邱傢煊 亓路宽

(北京工业大学建筑工程学院，北京 100124)

随着我国桥梁设计建设技术的日渐成熟，桥梁的耐久性越来越受到人们的重视，其中桥梁水害是严重影响桥梁耐久性以及安全的一个重要病害。当混凝土含水量增高时会加快有害离子在混凝土中的扩散导致混凝土容易产生碳化、碱骨料反应等有害现象，而且加重冻融循环对混凝土的破坏。桥梁排水系统在解决桥梁的水害问题中起到关键作用。

传统桥面排水系统[1]主要由桥面横纵坡、过水断面、泄水孔装置和管道系统四部分组成。目前桥面排水系统一般采用的排水方式为通过纵横坡将桥面水流汇流至泄水孔，最终通过排水管排入到地面排水设施或者河流中。但万剑平、金玉泉等[2,3]发现由于施工质量等原因泄水管与混凝土结合面不密实、排水管接头漏水、管道破坏破损、泄水管体脱落、泄水管内被堵塞等现象，水就会经由空隙渗入对桥梁耐久性带来不良影响。

为了解决该种桥梁病害本文提出了一种新型的泄水管用于降低当施工原因导致的泄水管缺陷以及泄水管失去排水作用时出现的渗水漏水现象对桥体带来的不良影响。

1 新型泄水管介绍

本文提出的泄水管在现有常用竖向泄水管基础上进行改进，在保有竖向泄水管的排水作用情况下在排水管外嵌套一个套管。套管分成两部分，其中上半部分为一个倒圆锥桶状结构，下半部分则是圆柱桶状结构。上半部分套管作用为当出现因施工误差或泄水管失去排水作用导致流体下渗时降低下渗的流体对周围混凝土耐久性产生的不良影响，其具体形式如图1所示。

2 混凝土渗流理论

将多孔介质理论应用到混凝土上就可以对微观上的混凝土渗流过程以宏观的渗流力学理论来予以描述。多孔隙介质在饱和或非饱和渗流过程遵从Forchheimer定律或者Darcy定律[4]，Forchheimer定律适用于渗流速度较大，属于非线性关系；Darcy定律适用于渗流速度较慢，属于线性关系。Forchheimer定律表达式可表示为：

(1)

其中,s为材料饱和度;n为材料孔隙率;vw为渗流速率;β为材料与速度相关的函数;ks为饱和度与渗透系数有关的函数;k为饱和时渗透系数矩阵；φ为测压水头。当Forchheimer定律中材料关于速度的函数β=0时，就会转化为Darcy定律。

研究表明[5]，达西定律可以推广到非饱和混凝土的水分传输中。Darcy定律虽为线性定律，但因为混凝土含水率的变化，水在混凝土中的传输速率也有一定的变化。张庆章等[6]以Xi等人研究为基础建立吸湿、排湿过程中毛细压力与饱和度之间的关系方程。其中排湿过程中的毛细压力与饱和度方程为：

(2)

(3)

其中,ρ1为水的密度；R为气体常数；M为水的摩尔质量；Ce为能量参数；kt为常数；Vm为单位水泥砂浆质量吸附水分子单程质量；W20为含水质量分数；S为饱和度；Pc为毛细压力。将式(2)代入式(3)即可得出饱和度与毛细压力之间的方程。Nguyen[7]发现在层流过程中，非饱和材料的渗透系数与饱和度的三次方线性相关，混凝土渗透系数与饱和度的关系式为：

ks=S3

(4)

3 数值分析

以现有的非饱和渗流理论为基础，然后对分析的问题加上一定的假设以及限制能够得出模型的数值解。Neuman[8]模型就是一种经典饱和—非饱和渗流的数值解模型，模型中饱和区中孔隙水压力为正压，非饱和区中毛细压力为负压，体现出非饱和区和饱和区间渗流运动的相关性。ABAQUS的非饱和渗流模块能够基于多孔介质非饱和理论较好地模拟。

3.1 数值模型

取泄水管周边1 m范围混凝土建立模型，上层为100 mm厚沥青混凝土铺装层，下层为220 mm厚梁体混凝土，两者间设有防水层，泄水管布置于模型的中心，套管嵌套在外，防水层采用不透水材料，在防水层与泄水管接合处设置3 mm缝隙模拟水入渗至梁体，见图2。

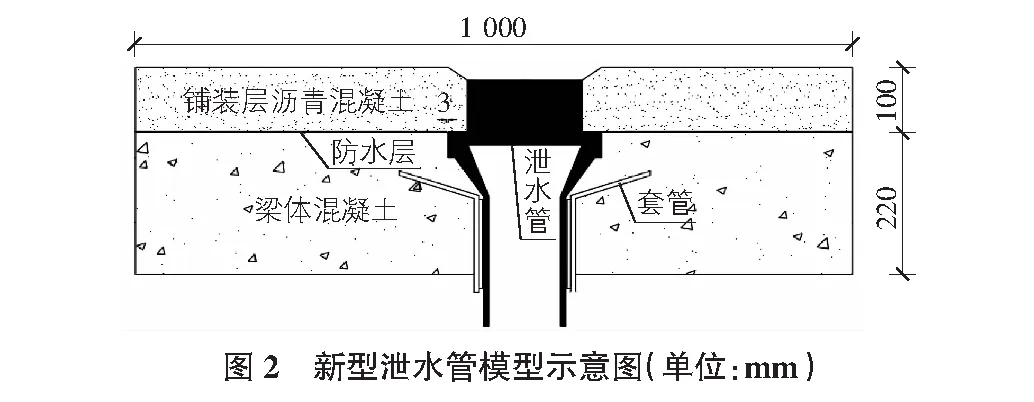
3.2 材料参数

材料饱和渗透系数的大小、孔隙率以及饱和度—渗透系数关系式等决定了在相同的边界条件下水在介质中的渗透速率。材料参数通过查阅文献、参考实验[9,10]数据得出，在模型中桥梁铺装层采用AC-13沥青混凝土，梁体混凝土采用C40混凝土，泄水管套管采用PVC材料，具体参数见表1。

表1 材料参数

为研究混凝土的非饱和渗流场，除定义基本的渗透系数、空隙率等参数，还需给定其孔隙压力—饱和度曲线，可通过式(2)及式(3)计算得出。

3.3 边界条件及初始条件

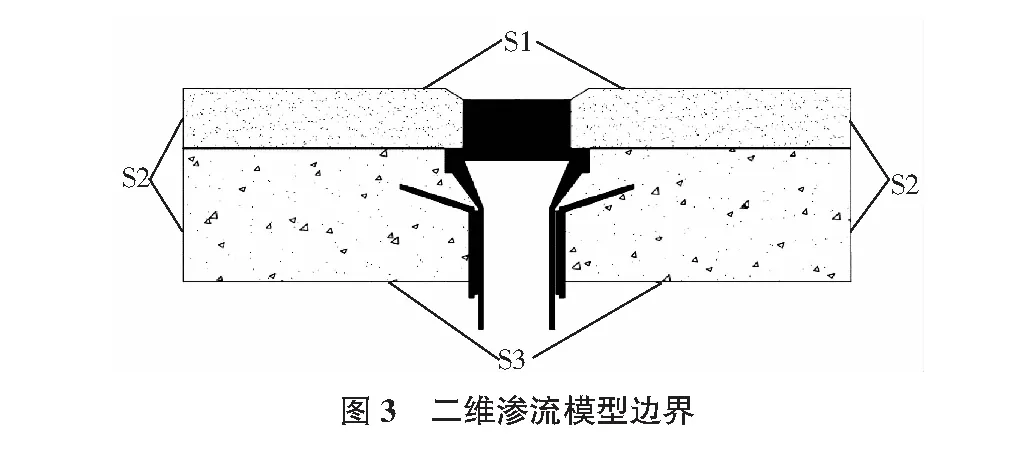
ABAQUS非饱和渗流模块中可以设定已知流量、已知水头边界、自由渗出段边界以及不透水边界。模型所设定边界条件见图3。

为了控制模型中的水渗入量，假定已知水头边界S1作为流体边界并将边界上孔隙压力设置为1 kPa,将两端S2设置为不透水边界，将下部悬空面S3设置为自由渗出段边界。初始条件定义模型中的初始孔隙压力以及饱和度，由于混凝土与空气中的水分存在交换，所以饱和度并不为0，参考混凝土的空气湿度—饱和度曲线将混凝土以及沥青混凝土饱和度定义为0.2，混凝土的初始毛细压力通过饱和度—毛细压力方程计算得出为19 MPa。

3.4 数值模拟结果

将上述边界条件以及材料参数输入模型后经过120 h分析后得出在分析时间内模型的饱和度结果。饱和度能够直观的反映水在模型内分布以及运动情况。

图4可以看出水在混凝土中的非饱和渗流并非线性过程，随着其饱和度的增大，其渗流速度也开始变快，饱和度随着距离的增加而减少。从图5可以看出新型泄水管中水集中分布于套管上部混凝土内而套管下方混凝土饱和度较小，并且套管上方混凝土饱和度分布较为均匀。

为得出不同时间点的数据以及饱和度分布的具体数值在模型中在竖向从1 cm开始每4 cm各选取4个点作为分析点得出结果。

表2 新型、普通泄水管竖向点集120 h时饱和度

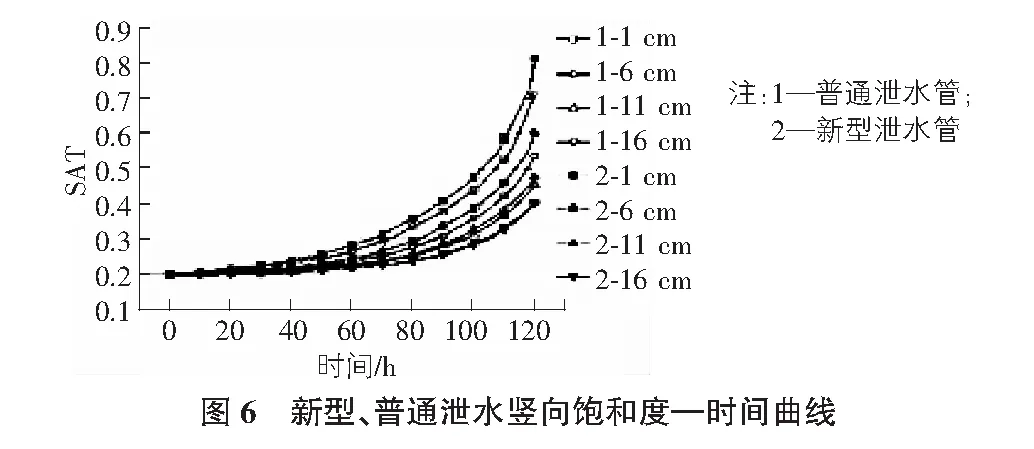
由表2以及图6可以看出，分析120 h内1 cm以及5 cm点处的饱和度数值均比普通泄水管的饱和度数值大，而9 cm及13 cm处的饱和度均比普通泄水管的小。这是因为所选取竖向点中1 cm以及 5 cm位于套管上方而9 cm以及13 cm点位于套管下方，由此可得套管对竖向入渗起到了阻挡作用，所以套管上方混凝土饱和度相较于普通混凝土较高，套管下方混凝土饱和度数值相较于普通泄水管较低。

4 结语

通过对提出的新型泄水管的数值模拟分析，主要结论如下：

1)水中泄水管周围的非饱和渗流过程并不是线性过程，渗流速度随着饱和度的增长而变快；

2)新型泄水管相对于普通泄水管在相同渗流量的情况下，新型泄水管通过其套管对水的阻挡作用能够有效防止水的竖向下渗，但由于水积聚在套管上部混凝土其饱和度会比普通泄水管情况下高。