精心设计,优化整合
——以一元一次不等式(组)复习为例
☉浙江省桐庐县实验初级中学 王良弟
在八年级数学复习阶段,为了让学生将知识系统化、明朗化,在期末考试中旗开得胜,笔者做了几个复习专题课.一方面,笔者整理了常考的知识点,另一方面,笔者认真分析了2018年一些地市的中考试题,从中分析了中考的考向和一些解题策略,编写进专题导学案中让学生再认知、再探究、再运用.
一、锁定目标,为学生明确复习方向
笔者深知复习过程不是简单的知识重复,而应该是知识的梳理、整合与应用.于是再次翻开课程标准,同时从网上查阅了近年来一些地市的中考试题,开卷有益.
在课程标准中,不等式内容的主要思想是进行数学建模,通过生活中的实际问题去培养学生学会质疑、解疑的能力,从而让学生认识到不等关系在生活中是一种重要的数量关系,其性质和解不等式(组)是数学的基本运算技能,也为今后进一步学习函数、方程和不等式打下坚实的基础.因此,在一元一次不等式(组)的复习专题中,必须把精准构建一元一次不等式(组)的解法和应用所学知识解决一些实际问题作为知识目标;将帮助学生认识建模思想和化归思想,在合作交流中内化分析能力、推理能力和解决问题能力,在解题探究中形成创新意识作为能力目标;将在积极参与、各抒己见中养成严谨的学习态度,提升探究问题的意识,提升思维的敏捷性,从而激发数学学习的欲望,增强在期末考试中对数学学科的信心作为情感目标.
二、梳理知识,为学生做好解疑铺垫
梳理知识时可以将课本上一元一次不等式(组)的知识点进行归类,让学生明确每个知识点的应用范围及它们之间的内在联系;能帮助学生准确把握一元一次不等式(组)内容的重点、难点,加深对各个知识点的理解和应用;特别是在做完相应知识点的训练后让学生学会归纳这个题所应用的知识点,便于在期终考试中遇到类似题时,能够沉着冷静,快速判断出解决这个问题应该应用的知识点.
在导学案编写时,笔者是这样梳理知识的.
知识点1:一元一次不等式(组)的概念.
用相关的数学语言,如“>”“<”“≠”“≤”等符号连接的式子称为不等式,含两个以上不等式的称为不等式组.在应用中还用到一些关键词,如“超过(不超过)”“多于(不多于)”“低于(不低于)”“至少(至多)”等.
对点练习1:让学生用不等式表示下列叙述的文字.
(1)x的4倍减去10大于2,x的2倍加上10小于2;
(3)a是不超过100的非负数.
创设目的:首先让学生理解不等式的基本概念,然后进行针对概念的练习,这些一元一次不等式(组)是建立在不等式的基础上的,尤其是第(3)小题,看似简单,却蕴含大世界,学生误认为“不超过”是“<”而忽视“=”,将“非负数”错误解读成“>0”,没有理解“0”也是非负数.让简单易错的练习为学生今后的解题敲响警钟,这是设计练习的关键所在.
知识点2:关于不等式的基本性质.
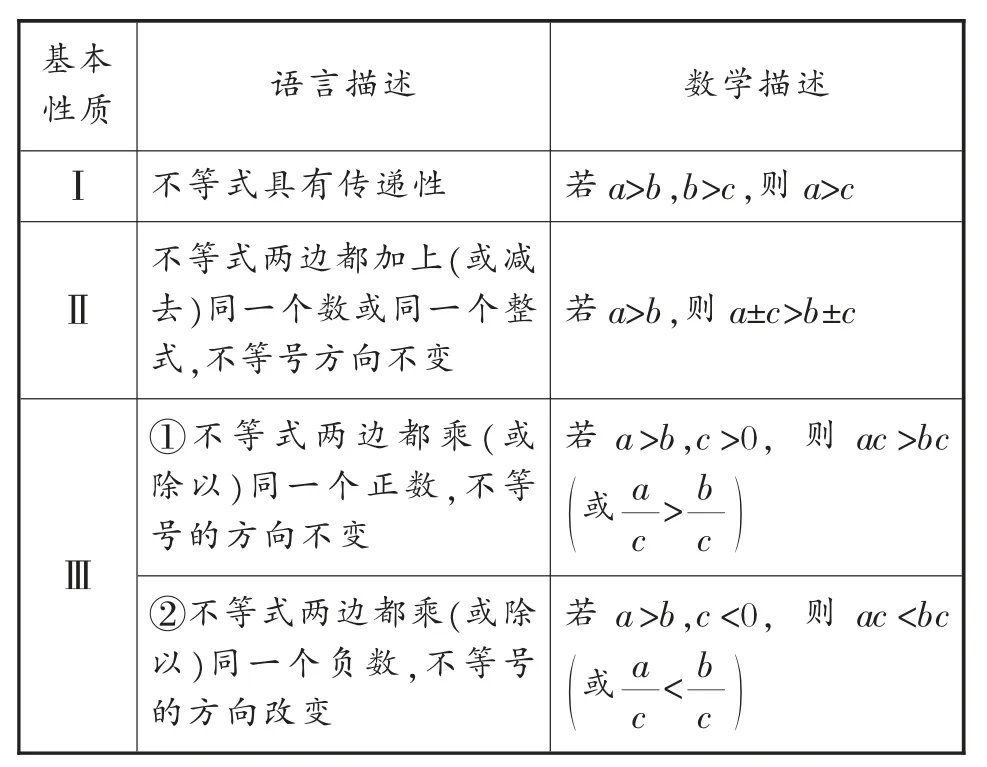
表1
对点练习2:用不等号填空:
(1)若ax≤by,则-ax+10______-by+10;
(3)若q<r,则qx_______rx.
创设目的:在学生对不等式的基本性质的再次认知后进行针对不等式性质的练习,有利于学生对不等式的性质的理解与巩固.第(1)小题的设置,检测学生对不等式性质Ⅱ和Ⅲ②的认知;第(2)小题的设置,检测学生对不等式性质Ⅰ和Ⅲ②熟练掌握的程度,某些学生仅仅会将不等式两边乘以之后,得出m<-6,而后“卡壳”;第(3)小题的设置,检测学生对不等式性质Ⅲ①和Ⅲ②的理解,学生仅仅作出x>0和x<0的讨论,而忽略x=0,让答案不完整.因此,在复习备考时,一方面,要注意基础,另一方面,还要考虑不等式性质的综合应用.
知识点3:关于不等式的解法.
(1)不等式的解集.
描述什么是不等式的解的集合(即不等式的解集).
(2)什么是解不等式?不等式的解集有哪些表示方法?
在课堂上强调不等式的解集的两种表示方法,即用不等式表示,或用数轴表示:大于开口向右,小于开口向左,有等号的画实心圆点,无等号的画空心圆圈(应用于一元一次不等式组更为方便).
(3)常见的解一元一次不等式的步骤.
去分母(同解一元一次方程)→去括号(不等式的基本性质Ⅲ)→移项(不等式的基本性质Ⅱ)→合并同类项→系数化成1(不等式基本性质Ⅲ).
对点练习3:求下列不等式的解,并在数轴上将解表示出来:
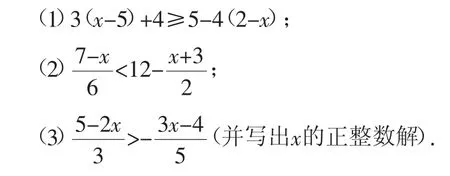
创设目的:在理解不等式的基本性质的基础上进行练习,有利于学生对不等式的解法的理解与巩固.给出的三个练习步步递进,第(3)小题要求写出x的正整数解,也是为不等式在生活中的应用奠定基础.
知识点4:一元一次不等式组的应用.
一元一次不等式组的应用这部分知识与解不等式是不可分割的,学会求解一元一次不等式也就轻松解决一元一次不等式组的求解了.但其应用则有着更深的内涵,需要学生在生活背景的练习中去体会.
对点练习4:(1)若是关于x、y的二元一次方程组,其中x-y<2,求实数m的取值范围.
(2)图1是关于x的不等式m-2x≥1的解集,那么,m的取值是_________.

图1
(3)随着生活质量的提高,越来越多的居民选购家用电饼铛.某小电器商场抓住机遇,从厂家购进了1-01、1-02、1-03三种型号电饼铛共x台,1-01型号电饼铛进价是120元/台,1-02型号电饼铛进价是160元/台,1-03型号电饼铛进价是280元/台.
①若x=200,购进两种型号的电饼铛共用去18000元,求1-01、1-02、1-03三种型号电饼铛各购进了多少台.
②为使每台1-02型号电饼铛的毛利润是1-01型号的2倍,每台1-03型号电饼铛的毛利润与1-01型号相等,且保证售完这200台电饼铛的毛利润不低于10000元,求每台1-01型号电饼铛的售价至少是多少元(注:毛利润=售价-进价).
③若商家购买的总费用为50000元,求x的最大值.
创设目的:小题(1)和(2)仍然采用数学的基本形式作为载体,旨在对数学问题的逐步深化,是让学生回归旧知、内化吸收的过程,而小题(3)则是生活中一种应用性的练习,有利于学生在练习中获取生活经验,同时让学生感悟到一元一次不等式组在生活中的应用比比皆是.因此,学好这部分数学知识是学生对生活热爱的追求,也是利用数学建模来提升学科素养的良好载体.
总而言之,八年级学习过程是一个关键阶段,期末考试备考复习可以有效提升学科成绩.此时数学知识的难度明显加大,学生往往顾此失彼,加强学法指导和增强备考意识是不容忽视的环节.所以,唯有锁定目标,为学生明确复习方向;梳理知识,为学生做好解疑铺垫,才能让学生在期末考试中胸有成竹.

