2020—2025年我国农科人才需求预测——基于灰色GM(1,1)模型的分析

刘志民，赵杏娜

(南京农业大学，江苏 南京210095)

引言

新世纪以来的中央第15个一号文件强调指出，当前农业发展仍是现代化建设的短板，农村建设仍是全面建成小康社会的短板。加快农业与农村发展，需要大批农业科技专业人才投身农业现代化建设，需要激发各类人才到农业农村创新创业的热情，也对农科人才提出了更高要求。那么未来我国农科人才的需求情况到底如何？据此，本文以2013—2017年农科毕业生有效供给数作为原始序列，拟通过灰色预测模型对2020—2025年我国农科人才的需求总量及结构层次情况进行分析。

在灰色预测方面，国内学者已有不少探索。罗党等(2003)指出灰色模型GM(1,1)应用广泛，可以根据模型的发展系数，调整模型的预测范围。通过构建不同的GM(1,1)模型背景值，输出模型时间响应函数和模型精确度检验表，对比了相互之间的特点，得出灰色模型的高精确度和强适用性，完善了模型的应用价值[1]。刘志民等(2010)对我国农科人才需求预测影响因素进行分析，采用灰色系统模型对我国农科人才需求总量及不同区域增长情况进行预测分析，研究结论为优化我国农科人才发展指明了方向[2]；江瑜和周志英(2009)首先论证了经济时代金融行业人才的紧缺和重要性，基于金融行业人才需求所呈现出的特征，选用灰色预测模型对未来几年的人才需求总量进行预测，并使用残差检验和后验差检验论证了模型的有效性，为有关部门实施人才管理提供科学的参考依据[3]。模型建立方面：张立(2011)构建企业人力资源模型以及灰色GM(1,1)预测模型，借助数学软件Matlab进行编程计算，将拟合值与实际值进行比较，发现灰色模型符合二级精度检验，说明灰色预测模型具备良好的预测实用性[4]；李少鹏等(2008)针对高校毕业生的供需情况构建了灰色GM(1,1)预测模型，运用定量与定性相结合的方法分析了毕业生的供需特点，为制定解决大学生就业矛盾的相关政策措施提供了参考依据[5]。徐荣，曹安照(2006)强调了社会进步与科技人才密不可分的关系，在研究科技人才的供给特征上，论证了灰色模型的适用性，因此构建灰色GM(1,1)模型，并做相关性检验，预测结果验证了模型的可靠性[6]。卞永峰，李恩平(2013)对山西省经济发展转型期所面临的人才短缺情况进行了分析，依据以往10年的科技人才数量构建了灰色系统模型，结合趋势外推法预测了未来年份人才需求量，研究结果为建设创新人才培养队伍指明了方向[7]。陶永坤等(2019)通过对科技人力资源增长趋势的判断，依据灰色系统理论预测模型对湖南长沙县科技人才增量进行分析，并将结果与实际值进行测评比对，结果证明了该模型的高精准度和可靠性[8]。冯长敏(2018)运用GM(1,1)模型对近几年北京春运铁路客运量数据进行预测分析，预测结果证明了灰色模型的良好精度，对现实中处理春运分流提供了很大帮助[9]。宋晨晓等(2018)在以往12年的数据基础上，将灰色预测模型与Matlab编程相结合，预测中医医院卫生人力资源需求情况，预测结果显示灰色预测精确度高，拟合效果良好[10]。王韦霞(2018)以安徽省某高校人员职称结构为案例，利用马尔科夫链和灰色预测模型对该校2019年教师总人数进行预测，通过预测结果总结该校师资队伍发展规律，为实现师资队伍的合理配置提供了参考价值[11]。以上研究既为本研究留存了探索的空间，又为本研究的开展提供了有益线索。

一、概念与模型选择

(一)农科人才

农科人才是指具有大专及以上学历，专门从事农业科研、技术、推广工作，具有较高创造力、能够为经济发展做出贡献的人。本文将农科人才在结构上分为四个层次：农科博士、农科硕士、农科本科及农科专科。在研究生教育层次，包含作物学、园艺学、农业资源利用、植物保护、畜牧学、兽医学、林学、水产八个一级学科[12]；在本科及专科教育层次，主要指农业院校设立的“目录内专业”，包含植物生产类、草业科学类、森林资源类、环境生态类、动物生产类、轻工纺织食品类、农业工程类、林业工程类、农林经济管理类[13]。

(二)人才需求预测

人才需求预测，就是指对未来一定时期内各种专门人才需求量的预测。应用预测技术可以预测出人才的需求量，同时可对未来人才的学历层次、数量等分别进行预测，在此基础上，结合各种外界因素，促进人力资源的合理利用和开发。本研究将对农科人才未来年份的人才数量规模及学历层次(农科博士、农科硕士、农科本科、农科专科)分别进行预测。本文对农科人才需求的界定为：人才需求=毕业生规模×就业率。

(三)预测模型选择

灰色预测模型称为GM模型，GM(1,1)表示一阶、单变量的线性动态灰(grey)模型(model)，用于时间序列预测的是其离散形式的微分方程型预测模型。GM(1,1)预测模型的实质是对原始数据序列作一次累加生成，使生成序列成一定规律，并用典型曲线拟合，建立其数学模型。灰色预测方法可以避免由于个人经验、知识、偏好等造成的人为主观臆断[14]。灰色预测模型能够对社会经济的行为特征和发展趋势进行整理和描述，总结系统发展内在规律，为系统预测研究提供参考意义。人才系统中既包含已知信息也包含未知信息，它与政治经济、社会发展之间的关系错综复杂，我们认为它是一个半明半暗的灰色系统，所以文章将采用灰色GM模型对农科人才需求量及各层次需求人数进行预测。灰色系统理论在研究数据序列较短、统计数据年份较少时能够呈现明显的变化趋势，预测建模时不需要了解原始数据的先验分布具体情况，也能反映出研究问题的真实趋势，具有较高的预测精度。灰色预测模型的这些优势，为其在人才预测方面打下广泛的基础。

(四)灰色预测模型建模与检验

1.灰色预测模型的建模方法及步骤如下[15]：

2.GM(1,1)的精度检验与预测[16]:

(1)事前检验

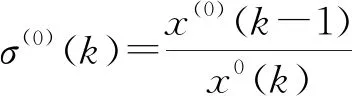
(2)事中检验

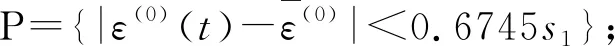
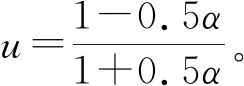
(3)事后检验

事后检验一般采用滚动检验。令X(0)为原始序列，Xi(0)为建模序列的4维新陈代谢子列。如：Xi(0)={X(0)(1),X(0)(2),X(0)(3),X(0)(4),}；X5(0)={X(0)(2),X(0)(3),X(0)(4),X(0)(5)}…对Xi(0)作GM(1，1)建模。滚动残差：

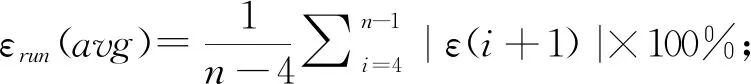
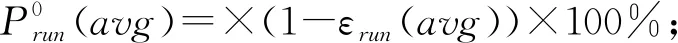
预测精度等级对照表，见表1：

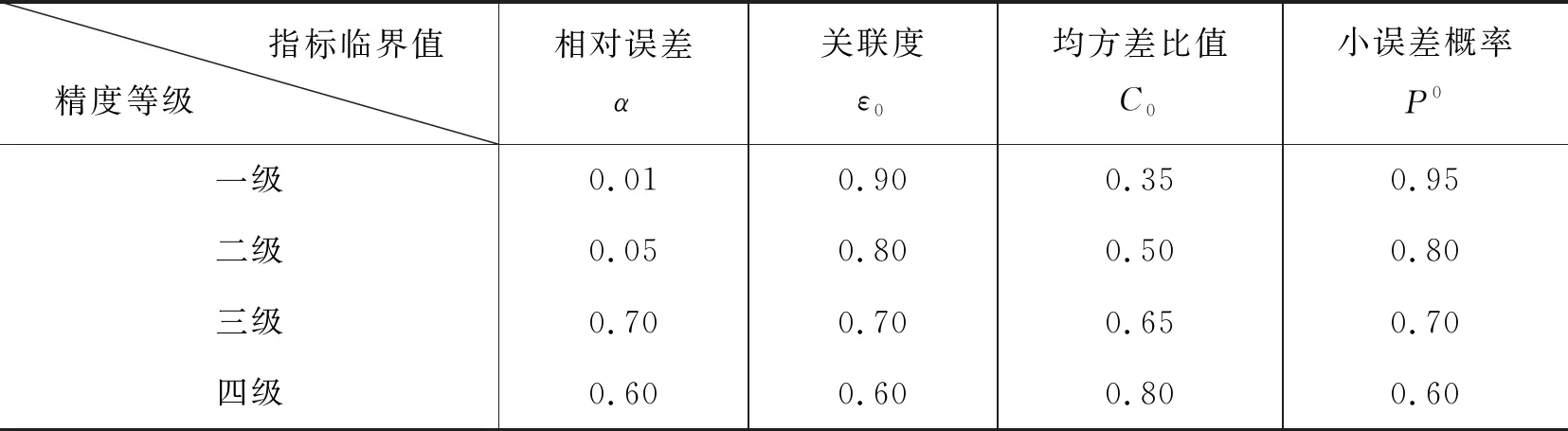
表1 精度检验等级参照表

二、基于灰色GM(1,1)模型2020—2025年农科人才需求总量预测

(一)灰色GM(1,1)模型建立

一般的，我们认为我国农科在校生数能够大体衡量农科人才的培养规模，但不能基于此来预测未来年份农科人才需求量。在对文献进行研读后，本文选择农科毕业生的有效供给数作为农科人才需求量的原始数列进行灰色GM(1,1)模型预测，即农科人才需求量等于农科毕业生数乘以当年平均就业率。2013—2017年农科毕业生有效供给数见表2：

表2 2013—2017年农科毕业生有效供给数(单位：人)

资料来源：由本课题组中国工程院子课题组统计数据整理计算得出。

对于农科人才总量的需求预测，首先对原始数据X(0)做一次累加生成，得到新的数据序列X(1)，给定原始时间2013—2017年资料序列见表3：

表3 2013—2017年建模数据序列 (单位：人)

构造矩阵B和向量Yn：

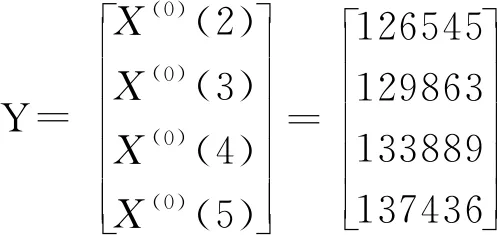
代入GM(1,1)微分方程，得：

其时间响应函数为：X(k+1)=9570139.205064e0.013692x-9439762.205064

(二)灰色GM(1,1)模型检验

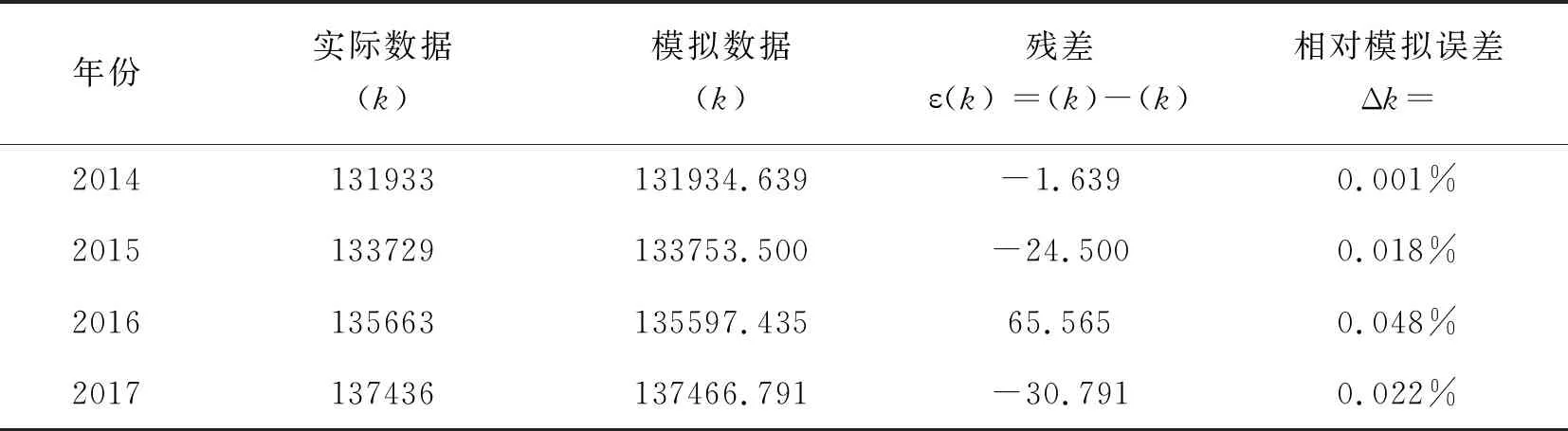
表4 GM(1,1)模型误差检验表

由表4可知，我们建立的灰色GM(1,1)模型，计算后的平均模拟相对误差为：0.023%，Δk<0.05，精度为二级。平均预测精度为：99.977%。灰色模型发展系数为-0.013692，a<0.1，表明模型可以进行中长期预测。从表5可以看出，预测模型通过高精度模型检验，说明建立的灰色预测模型非常成功，能达到较高的预测精度。

表5 模型精度检1验

注：A为每年农科人才规模模型检验值；B为较高精度检验参照值；C为高精度检验参照值。级比﹡用于检验建模序列是否是光滑序列，若序列光滑，则表明可以建立灰色模型。⨁灰发展系数-α用于检验模型预测范围的可行性。当-α≤0.3时，GM(1,1)模型可用于中长期预测；当0.3<α≤0.5时，模型可用于短期预测，中长期预测慎用；当0.8<α≤1时，应采用残差修正模型；当-α>1时，不宜采用GM模型。

(三)灰色GM(1,1)模型预测

2020—2025年每年农科人才需求总量预测结果见表6和图1。

表6 2020—2025年农科人才需求GM(1,1)模型预测值 (单位：人)

图1 2020—2025年农科人才需求预测结果(单位：人)

三、基于灰色GM(1,1)模型2020—2025年农科各层次人才需求预测

(一)灰色GM(1,1)模型建立

对各层次农科人才需求的预测，本文将重点分析各层次人才数量及在农科人才总量中所占比重的变化情况，具体分为农科专科、农科本科、农科硕士以及农科博士四个层次。以下建模数据是在各层次农科毕业生有效供给数基础上进行一阶弱化后所建立的灰色GM(1,1)预测模型，一阶弱化算子作用较为保守，用来消除数据不规则变动对预测结果的影响。原始数据为各层次农科毕业生的有效供给数，可以较为直观地反映不同层次结构人才需求量及所占比重的变化。灰色GM(1,1)模型的建模数列见表7：

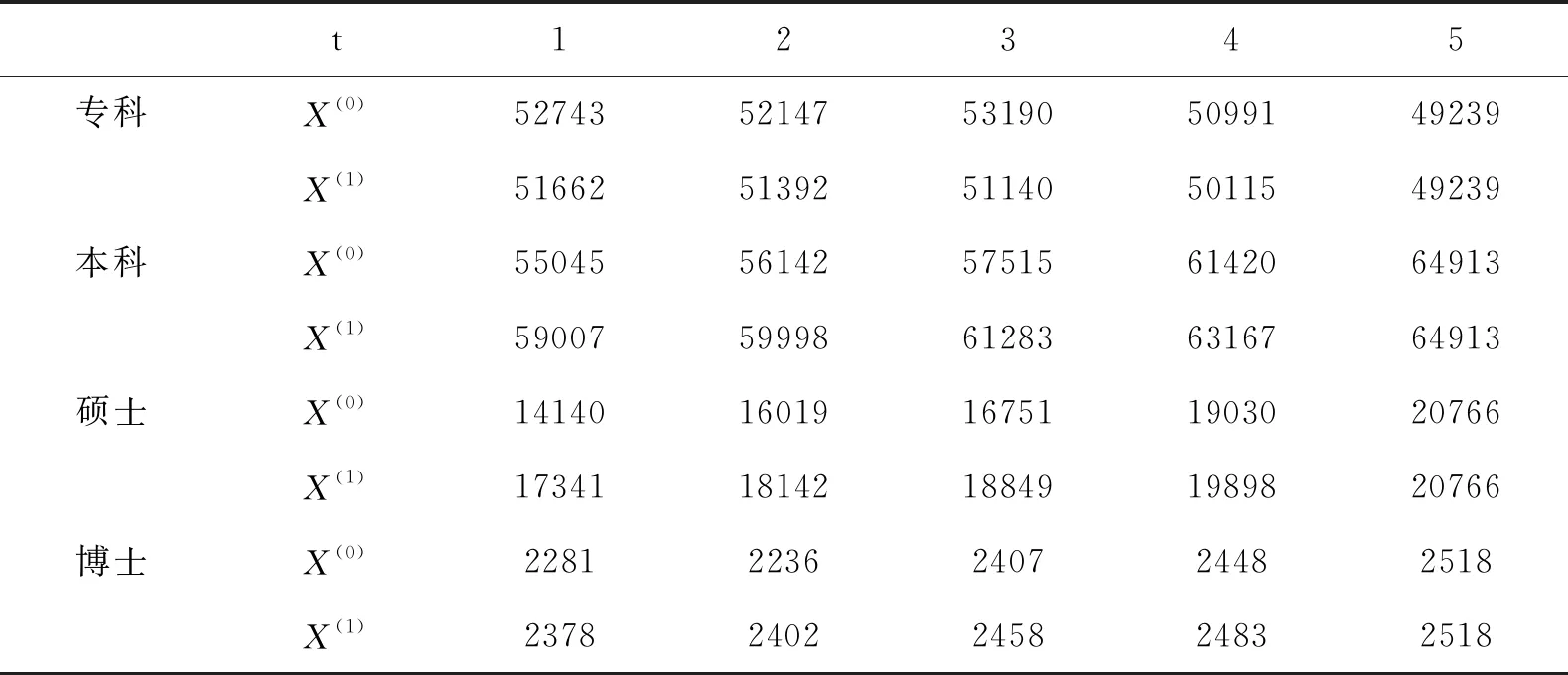
表7 2013—2017年各层次建模数据序列 (单位：人)

对原始数列X(0)进行一次累加，得到新数列X(1),作为建模数列。灰色GM(1,1)模型的参数估计值、白化方程及时间响应函数见表8：

表8GM(1,1)模型估计值及参数

(二)灰色GM(1,1)模型检验

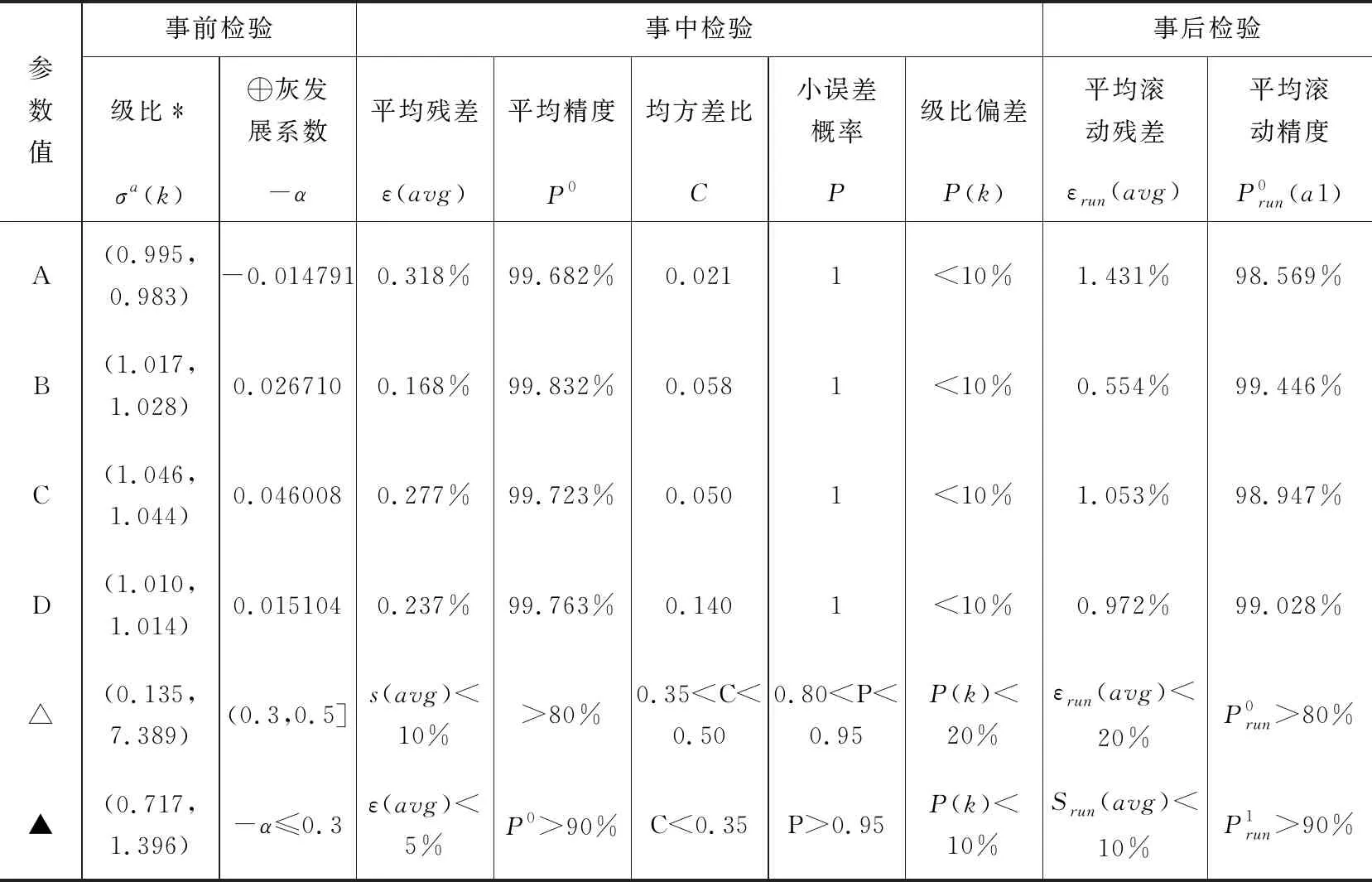
表9 GM(1,1)灰色模型检验精度检验

注：A为每年农科专科人才规模模型检验值；B为每年农科本科人才规模模型检验值；C为每年农科硕士人才规模模型检验值；D为每年农科博士人才规模模型检验值；△为较高精度检验参照值；▲为高精度检验参照值。级比﹡用于检验建模序列是否是光滑序列，若序列光滑，则表明可以建立灰色模型。⨁灰发展系数-α用于检验模型预测范围的可行性。当-α≤0.3时，GM(1,1)模型可用于中长期预测；当0.3<α≤0.5时，模型可用于短期预测，中长期预测慎用；当0.8<α≤1时，应采用残差修正模型；当-α>1时，不宜采用GM模型。

表9是灰色预测模型精度检验表，从检验的结果可以看出，无论是事前检验、事中检验还是事后检验，各指标均通过了高精度参数检验，各层次灰色预测模型的灰发展系数均小于0.3，表明GM(1,1)模型可用于中长期农科人才预测。模型的平均精度为99.75%，从上述的指标中可以看出，建立的灰色预测模型非常成功。

(三)灰色GM(1,1)模型预测

2020—2025年每年各层次农科人才需求预测结果见表10和图2。由此可知，2020—2025年博士需求量年均增长率为1.5%，到2025年我国农科博士需求量约为2845人；2020—2025年之间我国农科硕士需求量年均增长率为4.71%，到2025年，我国农科硕士需求量预测为30010人；对于本科层次的农科人才而言，2020—2025年之间我国本科需求量年均增长率为2.71%，到2025年，农科本科需求量预测为80306人，较2020年增加约一万人次；2020—2025年之间我国农科专科需求量年均增长率为-1.47%，农科专科生需求量呈逐年缓慢下降趋势。从侧面反映了在新常态背景下，对于农科人才的需求，更加注重培养结构的优化，聚焦于高层次、复合型人才。从各层次农科人才年均增长率来看，由快到慢的增长的分别是农科硕士、农科本科、农科博士以及农科专科人才。图2为各层次农科人才需求量情况，由图可知，除农科专科生外，农科本科、硕士、博士的人数是在逐年稳步增加的，说明社会对于高层次农科人才的需求不断增多。随着经济进入新常态，农业技术的转型升级，会对低层次农科人才产生一定的替代作用，对复合型农科人才的需求更加迫切。

表10 2020—2025年农科人才(层次)需求GM(1,1)模型预测值(单位：人)

图2 2020—2025年各层次农科人才需求预测结果(单位：人)

图3是各层次农科人才占农科总人才比例情况，我们可以看到，农科专科人才所占总人才的比例是下降的，由2020年的32.96%下降至2025年的28.59%；农科本科人才所占的比例将逐年上升，由2020年的46.06%上升至2025年的52.38%，约占农科总人才的一半；农科硕士所占总人才的比例也呈逐年上升趋势，由2020年的16.65%上升至约19.57%；农科博士占总人才的比例变化不大，各年份基本保持在1.85%左右，但总体呈缓慢上升趋势，也较为直观地反映出我国博士生的培养除规模和数量外，注重品质的提高，博士生的培养注重内涵式发展。全面建设小康社会，促进农业现代化发展，要牢牢把握“十三五”发展契机，加快新时代农业经济的发展，农科人才是关键。从以上预测的结果可以看出，在未来六年内，我国农业发展对农科人才的需求呈现平稳的增长趋势，从2020年的143231人到2025年的153380人，平均每年需要补充1692人。可以从以下两方面进行解释：一方面是基于新常态的时代背景，全国不同产业都进入转型发展新时期，农业产业也由原来的粗放式发展逐步转向集约式发展，农业经济增长更加平稳。对农科人才的需求不再盲目，而是更加注重层次结构的划分和人才的创新能力，以复合型农科人才需求为主。另一方面，在未来几年的人才培养过程中，除了保障农科人才总量的适量培养，农业经济的发展还要求适度增加农科博士生、硕士生、本科生的培养，减少农科专科生的培养，并且以培养高层次综合型农科人才为发展目标，不断满足农业经济发展的需求。

图3 2020—2025年各层次农科人才所占比例

四、结论

本文列出了经典GM(1,1)模型用于数列预测的步骤，对未来农科人才需求进行了总量和不同层次的预测，主要结论如下：第一，利用GM(1,1)预测模型对原始数据进行一阶弱化后建模，结果显示，模型的平均精度为99%以上，以一阶弱化后的结果为预测值具有较高的可信度；第二，从农科人才结构预测结果来看，未来六年我国农科人才的总需求量呈稳步上升趋势，2020—2025年我国农科人才需求预测数分别为：143231人、145206人、147207人、149237人、151294人、153380人。其中对专科生的需求量呈逐年下降趋势；对本科和硕士生的需求呈稳步上升趋势，且所占的比重在不断增加；对于农科博士而言，未来六年所占农科总人才的比重基本保持不变；第三，从各层次农科人才所占比例上看，高层次人才所占的比重在加大，也说明未来对复合型人才的需求将不断增多。