单箱双室曲线箱梁剪力滞效应分析
卢海林,郝 静,薛凯仪,蔡 恒
武汉工程大学土木工程与建筑学院,湖北 武汉 430074
箱梁是目前大跨度桥梁常见的主梁截面形式。箱梁在竖向弯曲时,由于翼板在其平面内的剪切变形引起翼板纵向应力沿横向分布不均匀的现象,称之为剪力滞效应[1]。多室箱梁由于多个腹板的支撑可实现更宽的桥面宽度,在大交通流量的公路和铁路桥梁中应用较为普遍,而曲线箱梁由于其更好的灵活性,可以在建设时避开地基沉降明显区域、建筑物不方便拆除的区域,在城市中心地带可以起到引导交通的作用,现在已经得到了普遍使用,故对多箱室曲线箱梁在弯曲变形时的剪力滞效应研究很有意义[2]。宁立等[3]针对髙速公路多室连续箱梁,通过空间实体有限元模型对一标准梁段进行了分析,揭示了边腹板部位的剪力滞效应大于其余腹板的现象。蔺鹏臻等[2]针对单箱双室箱梁,结合薄壁箱梁基本理论,解析了多室箱梁的剪力滞效应模式,揭示了不同剪力滞模式下的剪力滞分布规律。罗旗帜[4]提出了用有限段法分析剪力滞效应,该方法建立剪力滞微分方程的齐次解为位移模式,建立了平面单元有限段模型,将三维空间问题简化为一维空间。
有限元常用于分析混凝土箱梁剪力滞。孙学先等[5]对三跨连续刚构桥采用ANSYS板壳单元建立空间分析模型,研究了自重、预应力和活载下剪力滞的规律;牛斌等[6]针对预应力混凝土箱梁,建立了空间块体单元和模型试验,进行了剪力滞效应的研究。蔡恒等[7]直接从壳体结构特点出发,由8节点曲边四边形膜单元和基于Reinssner中厚板理论的弯曲单元推导考虑剪切闭锁效应的薄壁箱梁空间壳单元刚度矩阵及相应的刚度方程,并在MATLAB上编制相应的计算程序。通过数值算例,将理论计算值与ANSYS有限元结果,验证了理论公式推导的正确性与可靠性。朱松波等[8]建立了曲线箱梁剪力滞效应分析ANSYS模型,分析其在地震作用下的剪力滞效应,同时进行地震模拟振动台试验,研究了试验模型在地震作用下的剪力滞效应,验证了数值模拟的可行性;满自亭等[9]使用空间板壳有限元法分析了在对称集中荷载及均布荷载作用下曲率半径、宽跨比等结构参数对连续宽体曲线箱梁桥剪滞效应的影响。杜清等[10]运用有限元分析的方法,通过能量变分原理导出了薄壁箱梁的控制微分方程组,利用MATLAB依此推导出2个集中力、3个集中力作用下的解析解,并归纳出多个集中力作用情况下的解析解,建立了简支箱梁算例。蔺鹏臻等[11]基于横截面的荷载等效原理与荷载分解,分析了单箱双室箱梁对称弯曲时的局部扭转效应。并基于截面的剪力流平衡和箱室受力分解,得到了局部扭转的等效荷载及应力计算式。这些研究成果表明了有限元法对于剪力滞效应研究的科学性,分析结果可以用于宏观掌握结构的受力规律。
能量变分法是近年来研究剪力滞效应比较普遍的一种理论方法,甘亚南等[12]以能量变分原理通过控制微分方程和边界条件,据此获得几种常用边界条件方程,提出一种能对工程中常用矩形薄壁箱梁自振特性进行分析的方法;蔺鹏臻等[13]利用势能变分原理,建立了单室混凝土箱梁的剪滞效应分析方法,并改变翼板厚度研究了混凝土箱梁翼板厚度变化对剪力滞效应的影响规律。
由于直线箱梁研究未考虑弯扭耦合,产生的破坏特征不是很明显,而曲线箱梁不仅会产生强烈的弯、扭、剪力滞耦合变形,截面还会发生畸变、翘曲。基于此,本文采用有限元法,使用ANSYS有限元软件[14]建立了单箱双室曲线箱梁有限元模型,将单箱单室箱梁作为对照组,分别研究其在各工况下的剪力滞效应变化规律。
1 剪力滞效应机理
1.1 剪力滞效应机理
在箱梁分析理论中,箱梁的空间力学行为总体上包括对称纵向弯曲(产生剪力滞效应)、扭转、畸变和横向弯曲等4种效应[15]。剪力滞效应是箱梁在纵向对称弯曲变形时的主要力学行为,对箱梁强度和刚度的影响最为突出,因此很有必要对其进行研究。
当使用经典一维初等梁理论[15]进行分析时,其任意截面处的弯曲正应力表达式为:
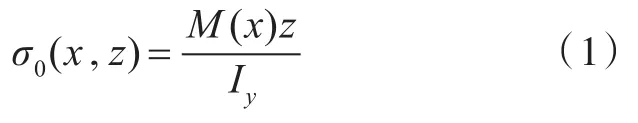
式(1)中:M(x)为x截面上荷载p作用下的竖向弯矩;Iy为截面绕y轴的惯性矩;z为计算点(x,y,z)距离中性轴的距离。
由式(1)可以看出,对于截面高度z处,沿横向任一点y处的纵向应力大小相等,未考虑由应力集中导致的应力分布不均匀现象,这也从理论上说明初等梁理论无法考虑箱梁的剪力滞效应。
1.2 剪力滞系数
在箱梁剪力滞效应的经典理论中,通常引入剪力滞系数λ来反应截面剪力滞效应,表达式为:

式(2)中:λ为剪力滞系数;σ为实际翼缘板应力;σ0为初等梁理论算出的翼缘板应力。通过剪力滞系数的变化情况可以得到剪力滞的分布规律。
根据剪力滞效应的基本机理,单箱单室曲线箱梁在受力弯曲时,竖向剪力由左右两侧腹板分别承担,由于曲线箱梁的内外侧剪力分布不均,故存在剪力滞后不等的问题,会造成内外侧的剪力滞系数不同。
而对单箱双室箱梁而言,受截面弯曲变形时剪力流分布规律的影响,一般情况下中、边腹板分担的竖向剪力一般均不相等,因此中、边腹板剪力滞效应也必然不相等。因此,对曲线箱梁剪力滞的分析很有意义。
2 剪力滞效应数值分析
2.1 模型概况
箱梁的材料和截面尺寸参考文献[16],为有机玻璃加工成的曲线箱梁模型,截面尺寸如图1所示。
材料参数:弹性模量E=3000MPa,密度ρ=1180kg/m3,泊松比为v=0.385。
几何参数:如图1标注,翼板宽度b1=100 mm,顶板宽度=底板宽度=2b2=200mm,上下翼板t1=t2=8mm,腹板厚度tw=8 mm,箱梁高度h=100mm,曲率半径r=2000mm,曲率角θ=30°,桥梁纵向长度为l=1309mm。
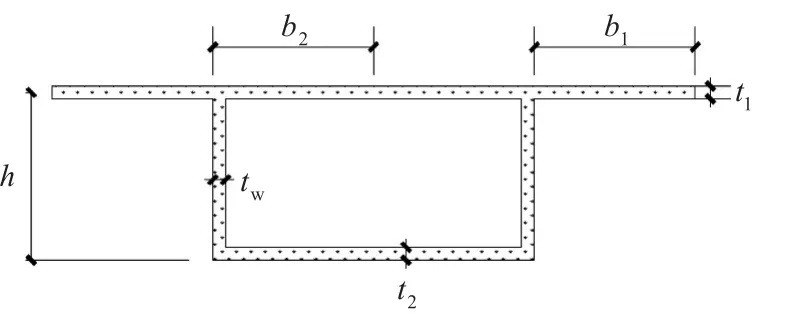
图1 单箱单室箱梁截面Fig.1 Cross section of single-box single-cell box girder
将受力按照箱梁空间力学分解,如表1所示,荷载分配模式有以下3种:
1)只有翼缘中部承担集中力,两边腹板为0,中腹板为p,如工况一所示;
2)2个腹板均匀分担集中力,即两边腹板均为p/2,如工况二所示;
3)3个腹板部位均匀分担几种荷载p,即各腹板均为p/3,如工况三所示。
单箱单室箱梁做为对照组,与单箱双室箱梁的施加荷载方式相同。
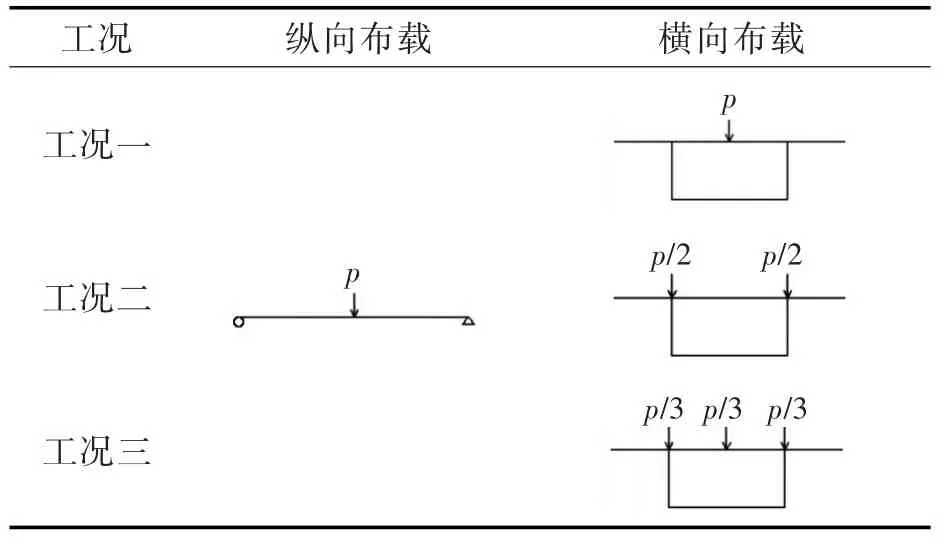
表1 箱梁不同加载模式Tab.1 Load models of box girder
荷载类型为集中力,取p=500 N,集中力的大小对有限元中剪力滞大小没有影响,建立好模型后对其进行静力求解。
2.2 有限元模型
采用ANSYS中的SHELL63单元建立曲线箱梁简支有限元模型,采用三维四面体单元划分网格,命令流为mshape,1,3D;划分网格的方式为映射网格,命令流为mshkey,0。
模型沿边界线每20 mm划分一个单元,因此横向单箱单室箱梁一共划分2128个单元,单箱双室由于有多余的中腹板划分了2296个单元,由于只考虑集中力影响,因此不用考虑非线性变化。
在箱梁底部四个边界角节点处施加支撑,约束节点的平动自由度,使其简支,建立好模型后根据不同工况施加荷载,并采用静力分析模块进行计算分析。
曲线箱梁有限元模型如图2所示。
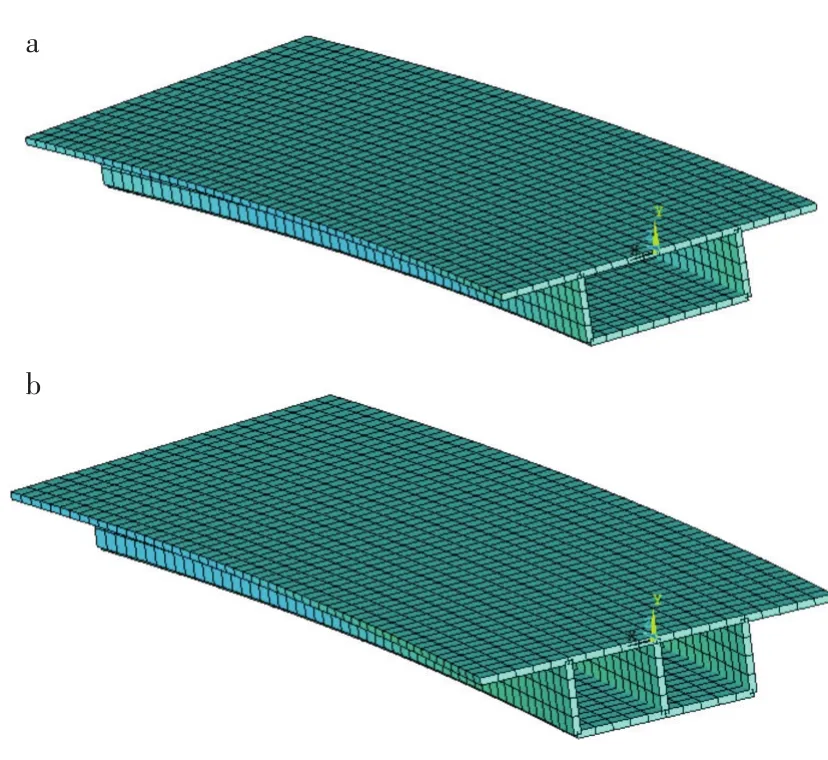
图2 有限元模型:(a)单箱单室曲线箱梁,(b)单箱双室曲线箱梁Fig.2 Finite element models:(a)single-box single-cell curved box girder,(b)single-box double-cell curved box girder
2.3 不同工况下箱梁的剪力滞效应
简支梁在不同工况作用下,单箱单室梁和单箱双室梁跨中截面顶板剪力滞系数分布情况如图3(a)和图3(b)所示,选择跨中截面的原因是此位置直接承受荷载,剪力滞效应明显,有很好的研究意义。
由图3(a)可以看出:
2)箱梁内侧腹板与顶板交界处剪力滞系数要略大于外侧腹板与顶板交界处,这是与基本梁理论不同的地方之一。
3)不同工况剪力滞系数对比可以发现,集中力单独作用于中腹板(工况一)时,剪力滞系数极值是其中最小的,约为1.5左右;集中力平均分配于两侧腹板(工况二)时,剪力滞系数极值是其中最大的,可以达到1.9;集中力平均分配于3个腹板(工况三)时,剪力滞系数极值为1.8,与工况二相差不大。
综上所述,在工况二作用下剪力滞系数的波动幅度也最大,剪力滞效应最明显;而集中力单独作用时的剪力滞系数波动幅度最小,剪力滞效应最不明显。
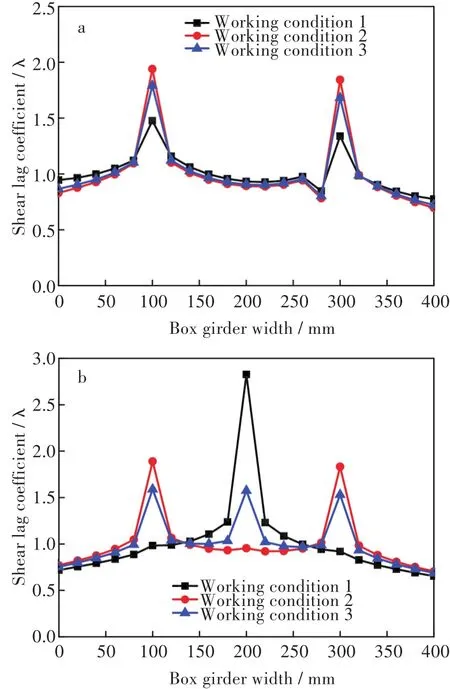
图3 不同工况下箱梁剪力滞系数:(a)单箱单室曲线箱梁,(b)单箱双室曲线箱梁Fig.3 Coefficient of shear lag effect of box girder under different working conditions:(a)single-box single-cell curved box girder,(b)single-box double-cell curved box girder
由图3(b)可以看出:
1)单箱双室梁腹板与顶板交接处同样表现出明显的剪力滞现象,不同的是当集中荷载施加于中腹板(工况一)时在中腹板处剪力滞系数出现了激增,最大值达2.8左右,原因是中腹板单独承担所有集中荷载,故产生了明显的剪力滞效应。
2)当每个腹板均匀分布3个力(工况二)时,3处腹板与顶板交接处剪力滞均匀分布,此时产生的剪力滞分布最均匀,剪力滞系数极值之间的差距最小。
综上所述,当单箱单室梁施加3个集中荷载(工况三)时,剪力滞系数极值差距最小,剪力滞分配均匀;而当单箱双室箱梁施加单集中荷载(工况一)时,中腹板处剪力滞系数出现激增,远大于边腹板处的剪力滞系数。
由于单箱单室与单箱双室在施加相同荷载情况下差别很大,所以需对相同工况下不同箱室梁的剪力滞效应进行分析。
2.4 相同工况下不同箱室梁的剪力滞效应
由图4(a)可知,单箱单室剪力滞内外侧腹板与顶板相接处节点剪力滞效应明显,符合理论判断,说明模型正确;单箱双室两边腹板与顶板相接处剪力滞不明显,而中腹板处有很大的剪力滞效应,剪力滞比单箱单室增加了近1倍。
由图4(b)可知,集中荷载平均分布在两边腹板时,两种箱梁的剪力滞差别不大,这表明剪力滞主要由腹板承受,中腹板由于几乎不承受应力,剪力滞系数为1。
由图4(c)可知,当集中力平均分布在3个腹板时,单箱双室在3个腹板处出现了明显的剪力滞,且边腹板处小于同样工况下单箱单室梁的剪力滞系数。这说明单箱双室梁板可以有效减小剪力滞效应。
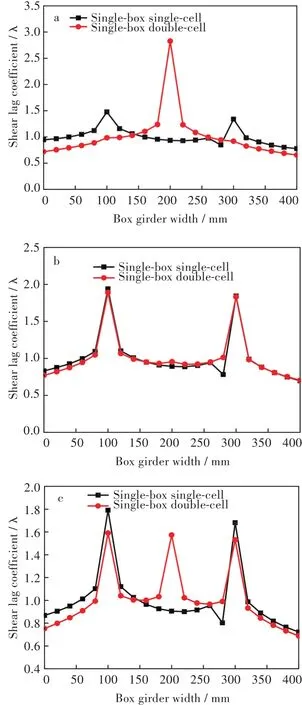
图4 相同工况下不同箱室梁的剪力滞:(a)工况一,(b)工况二,(c)工况三Fig.4 Coefficient of shear lag effect of different box girders under the same working condition:(a)working condition 1,(b)working condition 2,(c)working condition 3
3 结 语
通过对单箱单室和单箱双室混凝土曲线箱梁在不同工况下的对比分析,可以得出以下结论:
1)单箱双室混凝土曲线箱梁在各腹板均受集中力作用下各腹板均匀承担剪力滞,可以有效减小剪力滞系数峰值。但在单集中力作用于中腹板时,由于中腹板单独承力故剪力滞系数出现激增。因此在工程上可以使用单箱多室来分担剪力滞大小,但应防止只有中腹板单独承力,容易遭到破坏;
2)在原有集中力处增加腹板可以有效减小其它腹板处的剪力滞系数,但若其他腹板原本不承担荷载,而在有荷载处加上腹板会使施加荷载处应力激增,易出现应力集中现象。因此,在设计时应力集中区钢筋要布置密集些,否则易导致混凝土开裂;
3)由于曲线箱梁桥“弯扭耦合”的作用,内侧腹板剪力滞效应大于外侧;
4)单箱双室曲线箱梁做为多室箱梁中的代表,通过施加集中荷载这一简化荷载模式,得到的剪力滞效应分布规律大致符合理论判断;
5)限于篇幅本文仅分析了集中力荷载作用下单箱双室梁的剪力滞分布,若将单箱三室、多箱多室箱梁统一进行分析应能得到更加有意义的研究成果。
综上所述,在进行曲线箱梁设计时,要考虑到桥梁上部铺装荷载以及车辆荷载及其产生的剪力滞效应之后再考虑是否采用多箱室设计。若对箱梁剪力滞效应考虑不充分,可能会造成各种工程问题。
——超集中力
—— 梁在集中力作用点处的剪力分析

