基于GM模型和BP神经网络的西安市房价分析与预测

刘智禄 王慧丽

(西安财经大学 统计学院，陕西 西安 710100)

0 引 言

城市房价的波动影响着城市居民的生活，西安市作为西部重要的经济中心城市，从2016年开始，房价开始迅速上涨，特别是2017年以来，随着城市落户新政的实施，再次将房价问题推向高潮，引起了人们的广泛关注。因此，对房价影响因素的研究，并对未来房价的变动趋势进行预测，对于调控房地产市场有一定的借鉴意义。

在已有的研究中，学者们从不同角度分析了房价的主要影响因素。赵丽丽、焦继文从供给和需求两个方面选取房价影响因素指标，应用灰色关联度分析，得出各影响因素的相对重要程度。[1]74-75邱启荣、于婷运用主成分分析法对影响房价指标进行重新组合生成新的综合指标。[2]24-26杨中宣、杨洋洋从需求因素、供给因素和外界因素3个维度选取影响因素指标。[3]33-36在分析方法的选择上，大多数学者采用主成分分析、逐步回归等方法，不仅对数据的依赖程度很高，还伴有一定主观因素的影响，在变量确定后，建立的回归模型大都采用一般的统计模型。武秀丽、张锋采用时间序列分析法，对广州市房价数据建立预测模型。[4]5631-5635钟丽燕、高淑兰利用逐步回归法建立多元线性回归模型。[5]94-96还有学者应用灰色理论建立灰色系统模型进行预测。[6]22-24侯普光、乔泽群建立时间序列模型进行房价的分析预测研究。[7]20-23传统回归模型使用最小二乘估计法来估计模型的系数，但是当变量之间出现多重共线性时，会出现过拟合现象，使得模型的精度受到影响，甚至出现不合理的结论。

为了改善变量的选择方法，提高模型的拟合精度，本文采用Adaptive- Lasso 变量选择方法确定房价的主要影响因素，并将BP神经网络与灰色预测相结合，建立房价的组合预测模型，实现变量选择与参数估计同时进行，并对所建模型进行验证及对未来房价进行预测。

1 模型的构建

1.1 Adaptive-Lasso变量选择模型

多元线性回归通常是利用逐步回归法确定模型的解释变量，但是，在研究一些复杂的经济问题时，如果影响因素过多，利用逐步回归等子集选择的方法就会显得繁琐，所以，利用传统的变量选择方法就不够实用。正则化的方法则可以在传统最小二乘法的基础上进行改进，加入约束条件，依次防止系数取值过大，在减少变量的同时，处理线性模型中的过度拟合问题，其中，Lasso就兼备选择和收缩的功能，是一种将参数估计与变量选择同时进行的正则化方法。

假设所考虑的被解释变量为y，解释变量为xj，则在Lasso方法中，模型中变量xj的系数估计式定义见(1)式：

(1)

Lasso方法可以解决线性模型中的最小二乘法和变量选择时逐步回归出现的局部最优估计问题，但其自身也存在一定的局限性。从(1)式中可以看出，Lasso对所有的变量施加了相同的惩罚，因此，对非零参数估计的惩罚也相应变大，导致参数估计的偏差较大。为此，可以将该方法进行适当的改进，采取改进的Lasso方法进行变量选择，并给不同的参数系数赋予不同的权重，这样就可以解决上述问题，具体定义见(2)式：

(2)

1.2 灰色预测模型

灰色系统理论是我国著名学者邓聚龙教授于1982年提出的。该理论的研究对象为“部分信息已知，部分信息未知”的不确定性系统，通过对部分已知信息的生成、开发并实现对现实世界的确切描述和认识。[8]43-47

设变量X(0)={X(0)(i),i=1,2,…,n}为一非负单调原始数据序列，首先对X(0)进行一次累加，得到序列：X(1)={X(1)(k),k=1,2,…,n}。

下面对X(1)建立一阶线性微分方程，见(3)式：

(3)

即GM(1,1)模型。

求解微分方程，得到预测模型，见(4)式：

(4)

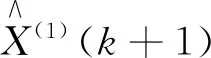
(5)

对所建立的模型进行检验，相应的后验查检验模型精度表如表1所示。

表1 后验查检验模型精度表

1.3 神经网络预测模型

人工神经网络是在现代神经科学的基础上提出和发展起来的，其工作方法是模仿人脑，旨在反映人脑结构及功能的一种抽象数学模型，即首先以一定的学习准则进行学习，然后才能进行判断评价等工作。[9]187-191有关的理论和方法已经发展成一门介于物理学、数学、计算机科学和神经生物学之间的交叉学科。BP神经网络是其中的一种网络模型，又称为反向传播神经网络，是一种多层次反馈型网络，通过对样本数据的训练，不断去修正网络模型中权值和阈值，从而使误差函数沿负梯度方向下降，来逼近期望的输出。[10]96-99该模型具有运算速度快，问题求解效率高、自学能力强、适应面宽等优点，多用于函数逼近、模型识别分类、数据压缩和时间序列预测等。三层BP神经网络模型见图1。

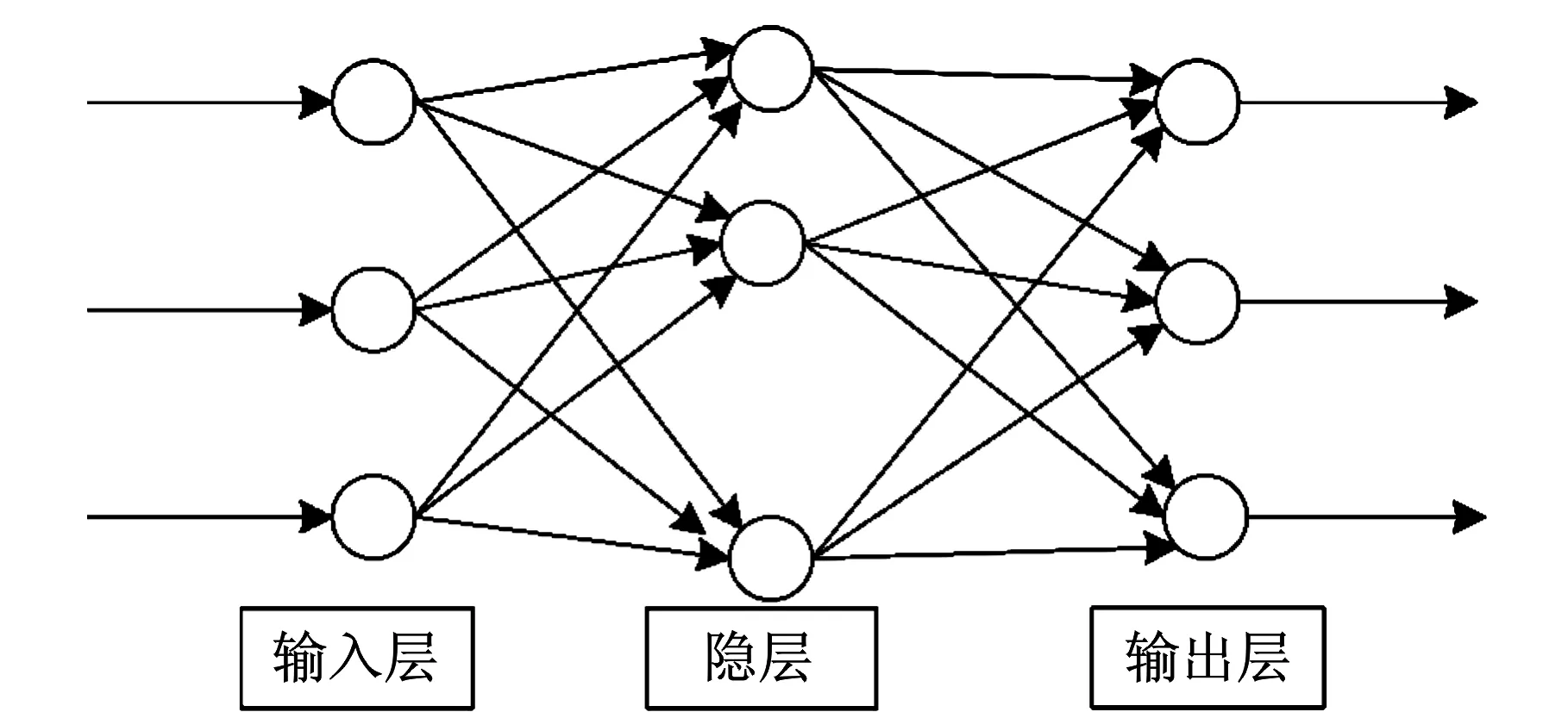
图1 三层BP神经网络模型

图1模型选用S型传递函数f(x)=1/(1+e-x)，定义反传误差函数见(6)式：

(6)

(6)式中，Ti为期望输出，Oi为网络的计算输出，通过不断调节网络权值和阈值使误差函数E达到极小。

1.4 灰色预测模型与神经网络的组合模型

由于灰色预测模型对小数据量数据具有很好的预测性，神经网络对历史数据信息能充分提取，从而预测和模拟的精度高，本文结合两者的优点，构建组合模型，以提高模型的预测精度和解释性。

下面利用Adaptive-Lasso方法建立选择变量模型来筛选变量，进而根据上述GM(1,1)模型对筛选出来的变量分别建立灰色预测模型进行预测，得到变量在 2018年、2019年的预测值；然后对历史变量数据建立BP神经网络预测模型，把通过灰色预测模型得到的预测值代入训练好的模型中，从而得到充分考虑历史信息的2018年—2020年西安市房价的预测值。组合模型的流程图如图2所示。

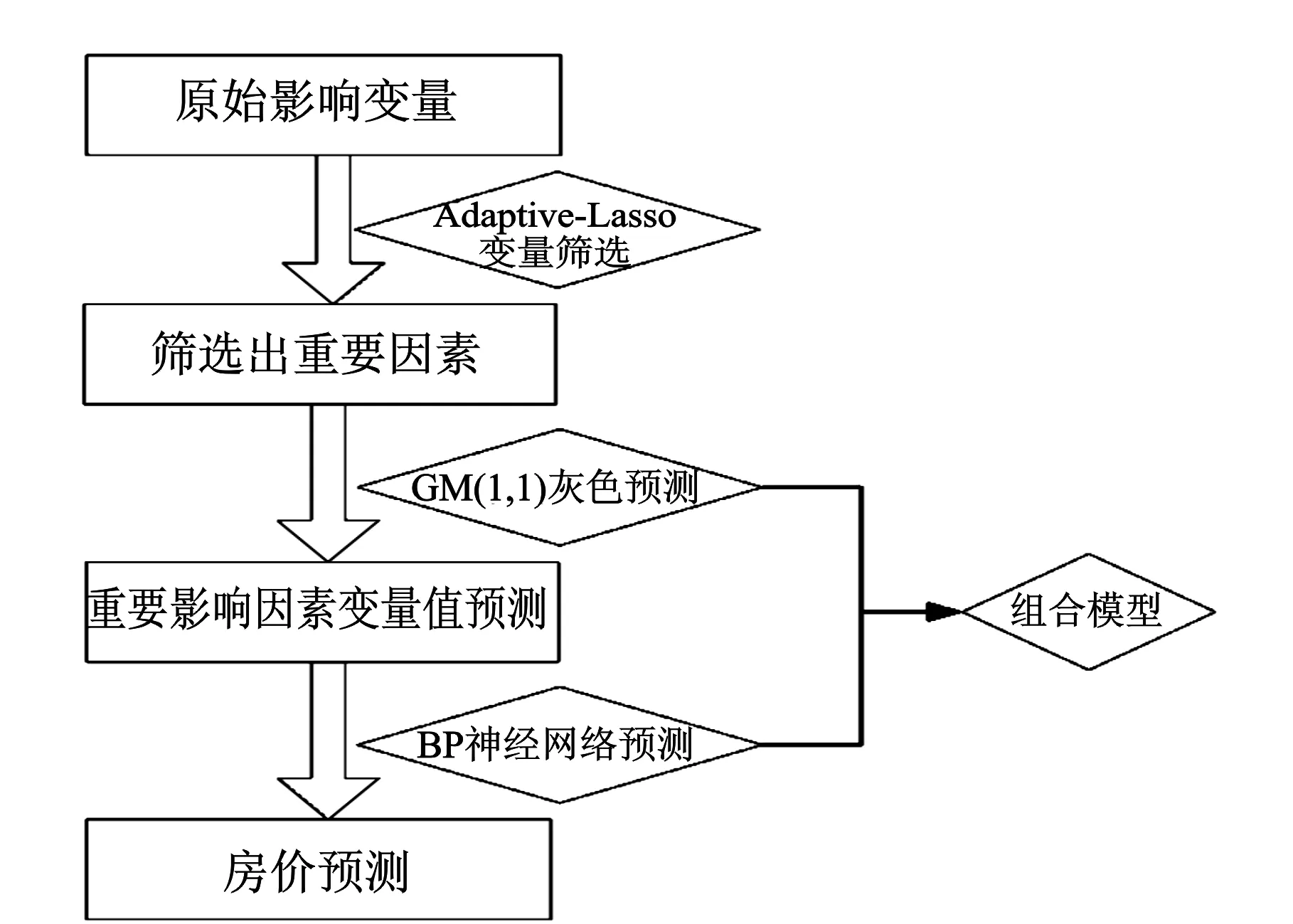
图2 组合模型流程图

2 实证分析

2.1 数据来源及影响因素的选取

本文借鉴袁芳的观点[11]477-478，综合考虑房地产行业的特点，选取以下13个影响因素(数据均来自《西安统计年鉴》)：

X1：西安市生产总值GDP；

X2：财政收入；

X3：城镇居民人均可支配收入；

X4：居民消费价格指数；

X5：城镇居民家庭的恩格尔系数；

X6：城镇居民人口；

X7：人口密度；

X8：房地产开发投资额；

X9：住宅竣工面积；

X10：住宅销售面积；

X11：住宅销售额；

X12：住宅出租面积；

X13：建筑业总产值；

Y：西安市住宅价格。

2.2 描述性分析

相关系数用来描述变量之间的相关关系，初步判断因变量与解释变量之间是否具有线性相关性。本文利用R语言实现变量间的相关性分析，表2给出了上述各变量间的Person相关系数矩阵。

通过相关系数检验结果，可以看出居民消费价格指数、住宅出租面积两个变量与西安市的住宅价格线性关系不显著，其余的变量中，除了居民的恩格尔系数与住宅价格呈高度的负相关关系外，其它的变量均与住宅价格呈现高度的正相关关系。

表2 变量Pearson相关系数矩阵

2.3 Adaptive-Lasso 变量的选择

通过R语言中的相关算法，编制程序实现Adaptive-Lasso方法的变量选择，变量选择系数见表3。

表3 变量选择系数

R-squared:0.999

由表3可以看出，居民消费价格指数(X4)、人口密度(X7)、房地产开发投资额(X8)、住宅竣工面积(X9)、住宅销售额(X11)、住宅出租面积(X12)、建筑业总产值(X13)，这些因素的系数为0，即在模型的建立过程中这几个变量被剔除了。

居民的消费价格指数(X4)、住宅出租面积(X12)与住宅价格(Y)的相关性太小；房地产开发投资额与建筑业总产值存在明显的共线性；人口密度、住宅竣工面积、住宅销售额也存在共线性；因此在使用Adaptive-Lasso 方法构建模型时，这些变量被剔除。通过以上的Adaptive-Lasso方法得到房价的预测模型为见(7)式：

Y=0.740 10X1-1.913 41X2+0.036 30X3+

112.132 98X5-4.484 81X6+2.390 71X10-1 630.717

(7)

2.4 住宅价格预测模型

2.4.1 灰色预测模型

基于西安市2001—2017年的房价数据，建立单一灰色GM(1,1)预测模型，并利用R语言软件实现GM(1,1)模型的预测值与房价真实值的比较曲线，如图3所示。

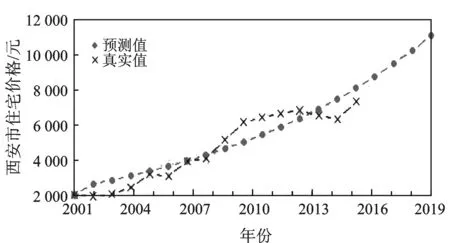
图3 GM(1,1)预测结果对比

图3说明利用GM(1,1)模型预测的房价走势和真实值的走势大致一致，但也存在一定的误差。

2.4.2 灰色预测与神经网络的组合预测模型

通过Adaptive-Lasso方法进行变量选择之后，对选择的变量构建灰色预测与BP神经网络的组合模型。将西安市生产总值GDP(X1)、财政收入(X2)、城镇居民人均可支配收入(X3)、城镇居民家庭的恩格尔系数(X5)、城镇居民人口(X6)、住宅销售面积(X10)，这些经济指标2018年和2019年的预测数值通过R语言建立灰色预测模型进行计算，灰色预测模型相关因素精度见表4。

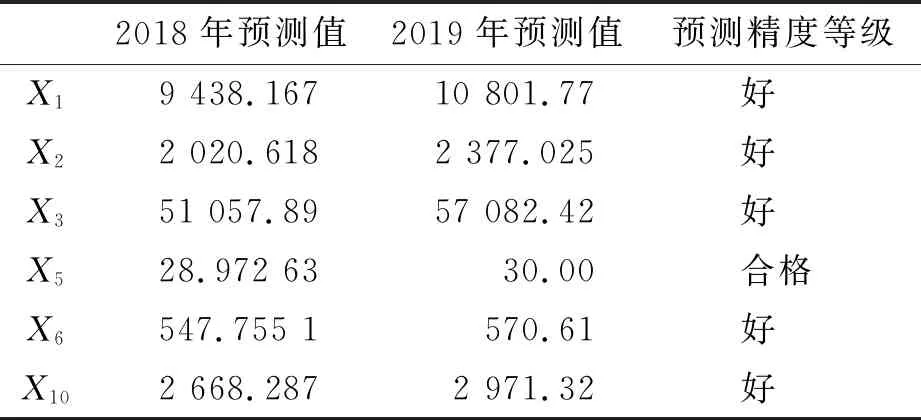
表4 灰色预测模型相关因素精度

由于BP神经网络对历史样本数据模拟具有较好的精度，因而将上述变量的预测值代入建立的BP神经网络预测模型，由此可得西安市2018—2020年的房价预测值，真实值与预测值的比较结果如图4所示。

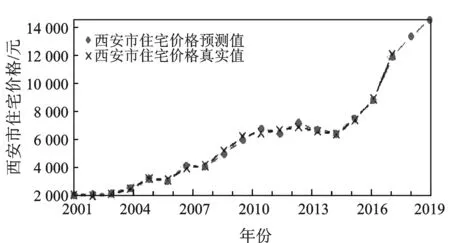
图4 组合模型预测结果对比

由图4可知，组合模型预测的房价走势基本和真实值走势相同，可见，该模型的预测效果较理想。

2.4.3 模型对比

通过对单一灰色预测模型与组合模型的预测结果比较，得出模型的预测结果对比情况。见表5。

GM(1,1)模型的预测值、组合模型的预测值以及真实值的对比曲线如图5所示，相应的模型的预测误差对比如图6所示。

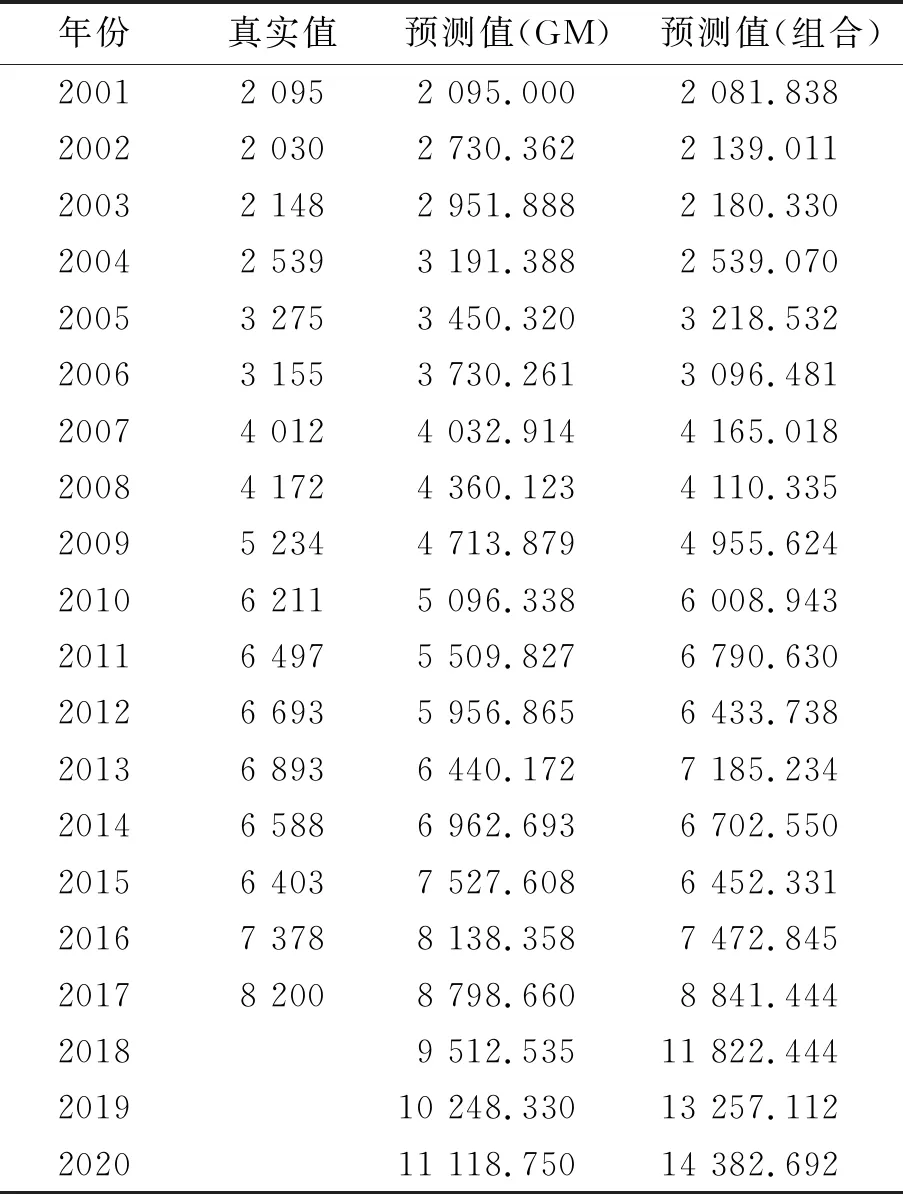
表5 模型的预测结果对比情况

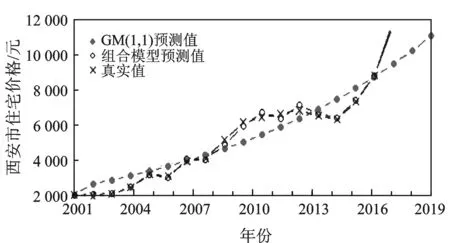
图5 模型预测结果对比

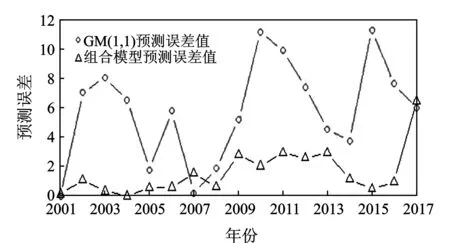
图6 GM(1,1)模型与组合模型的预测误差对比

由单一灰色预测模型与组合模型的预测结果可以看出，西安市房价处于上升趋势，尤其是近几年的上升幅度较大。根据图6模型预测误差对比情况可知，利用GM(1,1)灰色预测模型预测的房价与真实值的误差大于利用灰色预测和BP神经网络组合模型预测的误差，判断组合模型的预测效果比较好。

另外，灰色预测模型仅仅基于房价历史数据进行预测，而组合模型将与房价影响程度较大的因素充分考虑在模型中，通过这些变量来预测房价的走势，更具有解释性和理解性。

3 结 语

基于西安市2001—2017年影响房价的经济指标历史数据，首先建立了Adaptive- Lasso变量选择模型，确定西安市生产总值GDP、财政收入、城镇居民人均可支配收入、城镇居民家庭的恩格尔系数、城镇居民人口和住宅销售面积等六项因素是影响西安市住宅价格的主要因素。在此基础上，对选择的变量构建了灰色预测GM(1,1)与BP神经网络的组合模型，从而对未来的房价进行预测，通过对比发现预测的房价与真实值比较吻合，同时，该组合预测模型与单一使用灰色预测模型来预测房价相比，能够充分考虑历史数据，将影响因素指标也考虑在模型中，具有较好的解释性和可理解性。