直驱式永磁同步风力发电机轴电流问题分析

刘瑞芳 孟延停 任雪娇 王芹芹

摘要：直驱式永磁同步发电机是目前风力发电系统中广泛采用的形式之一。由于它需通过变流器向电网供电，变流器产生的高频共模电压经过电机的杂散电容耦合会引起轴电压，继而产生轴电流，会导致轴承产生早期失效，因此有必要对轴电流进行准确的预测并开展轴电流抑制方法研究。本文针对一台2.1Mw直驱永磁同步发电机基于电磁场数值计算获取了电机内杂散电容参数，并提出了等效三导体模型来简化等效电路。对轴承分压比进行了灵敏度分析，并据此讨论了轴电流的抑制措施。最后搭建变流器一发电机系统轴电流仿真模型，分析了屏蔽法和电刷接地法两种轴电流抑制措施的效果。结果表明，这两种方法可以有效抑制轴电流，但不能用于抑制共模电流。

关键词：直驱式永磁同步发电机;轴电流;共模电压;杂散电容;轴承分压比;抑制方法

DoI：10.15938/j.emc.2019.08.006

中图分类号：TM315文献标志码：A 文章编号：1007-449X（2019）08-0043-07

0引言

风力发电是目前发展最快的清洁能源。国内外兆瓦级以上的风力发电机组多采用双馈异步型和永磁同步型。与双馈异步型发电机组相比，永磁同步型发电机组具有能量密度高，无需励磁绕组，运行效率高;无需集电环和电刷，可靠性高;转子永磁式，结构和维护简单等特点。随着海上风电技术的快速发展，以永磁同步发电机（permanent magnet synchro-nous generators，PMSG）为核心的风力发电系统已成为广泛使用的形式之一。永磁同步风力发电机又分为直驱式和半直驱式。其中直驱式永磁同步发电机因其直接驱动、高效、高可靠性等优点，已经成为并网风力发电技术的发展趋势。

永磁同步风力发电系统中发电机经过变流器向电网供电。变流器的开关器件工作时会产生高频共模电压，并通过电机杂散电容网络的耦合作用，在轴承内外圈之间产生轴电压。当轴电压超过轴承滚珠与滚道问润滑脂的油膜阈值电压时，润滑油膜发生击穿，产生放电现象，引发轴承过早失效，继而引起发电系统损坏等不良后果。因此准确获取杂散电容，建立轴电流分析模型，通过预测轴电流并分析相关的抑制措施具有重要的工程意义。

文献[5]发现1～2MW风力发电机的轴承电腐蚀故障率高达70%。目前针对双馈异步发电机轴电流问题已经有过许多研究，而永磁同步发电机的轴电流问题研究还比较少。其中文献[10]对直驱式永磁同步发电机内部杂散电容进行了解析计算，建立了四导体系统的轴电流分析模型。但是其解析计算忽略了导体问的相互作用;且所建立模型中的电容参数多，轴承分压比计算复杂，需要对其进行简化分析。本文将围绕直驱式永磁同步发电机的杂散电容进行基于多导体部分电容理论的参数计算。以轴承分压比为基准对电容网络进行简化建模，最后建立变流器一直驱式永磁同步发电机系统的仿真模型，进行轴电流预测，并分析轴电流的抑制措施。

1直驱式永磁同步发电机的轴电流模型

1.1直驱式永磁同步发电机杂散电容计算

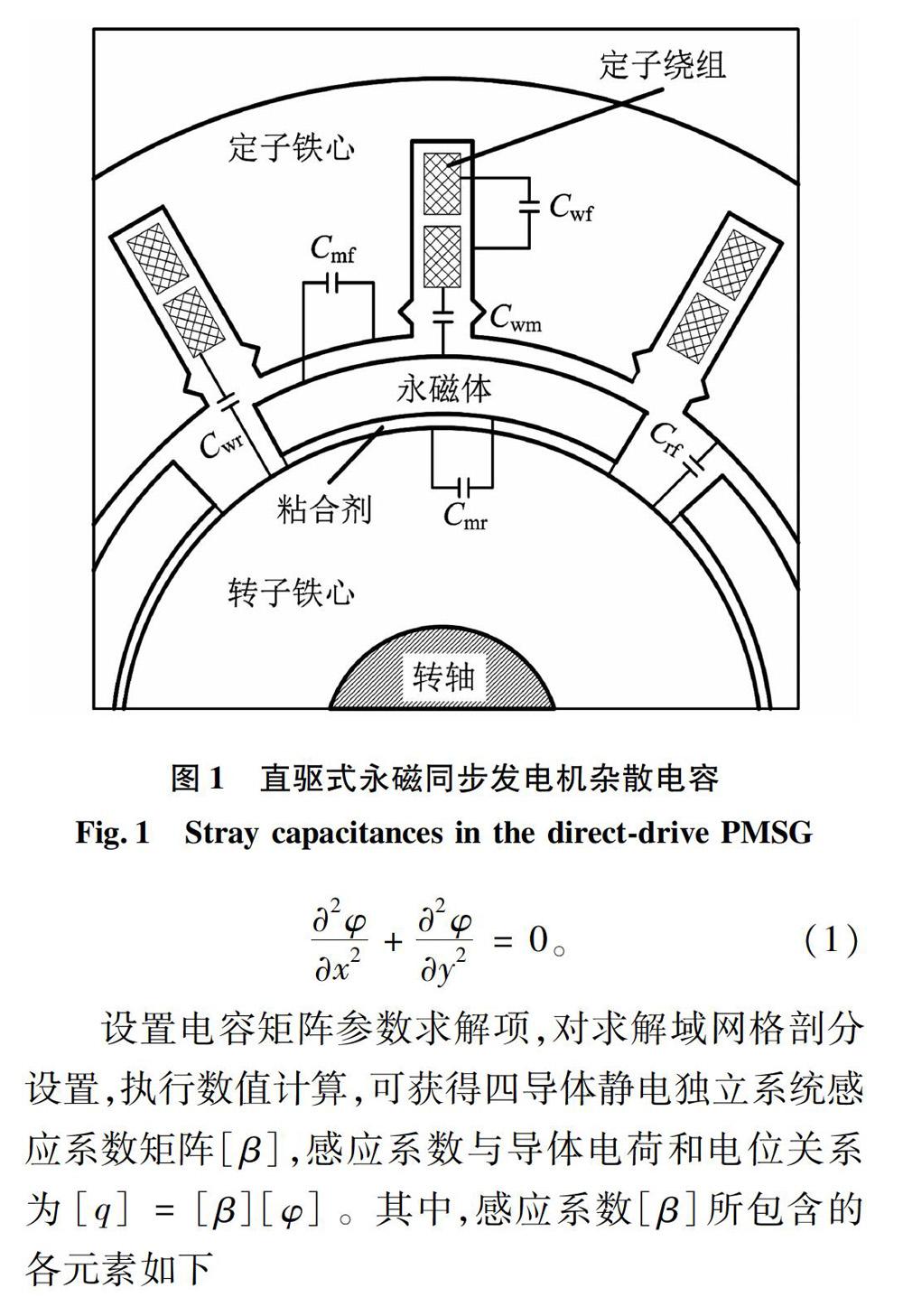
直驱式永磁同步发电机的永磁体一般采用表贴式安装，即永磁体通过特定粘合剂直接黏连在转子铁心的外表面上。发电机定子绕组、转子铁心、永磁体和定子铁心（机壳）4个部分形成四导体静电独立系统，根据多导体系统部分电容理论，两两导体问存在电介质材料，从而形成杂散电容。如图1所示，定子绕组与定子铁心问的杂散电容Cwf，定子绕组与转子铁心问的杂散电容Cwr，转子铁心与定子铁心问的杂散电容Crf定子绕组与永磁体问的杂散电容Cwm，转子铁心与永磁体问的杂散电容Crm以及永磁体与定子铁心问的杂散电容Cmf。

采用基于两导体电容器的解析公式来进行电容的计算，不能计及多导体问的耦合作用，且在计算中要进行许多假设。如果要综合考虑电机的实际复杂结构和多导体之间的相互作用，应当采用基于有限元法的电磁场数值计算进行电容耦合参数的求解。

忽略电机端部效应，在Ansys Maxwell中建立2D模型，选择静电场求解器，对各部件设置材料属性。设定子铁心电位为参考电位，对定子绕组、转子铁心以及永磁体分别施加不同的电压激励，电场中各点的电位ψ满足拉普拉斯方程

在Ansys MaXwell中建立1/12电机的2D模型。由于电机中各种媒质的介电常数为常数，不随激励的变化而变化。因此电压激励大小对电容参数计算没有影响。在计算定子绕组对定子铁心的电容时，将全部定子导体设为一个等效电极，这是因为电机三相绕组不论是星形还是三角形联结，都可以通過端部接线把各槽内的导体连起来。在静电场中计算分布电容时，就可以将其视为一个等效电极。在进行电容参数计算设置，对定子绕组、永磁体、转子铁心以及定子铁心添加电压激励，分别为2V、1.5V、lV和0V，并将定子铁心设置为接地。其电位分布如图2所示。

计算获得的电机杂散电容结果如表1所示。

1.2直驱式永磁同步发电机的轴电流模型

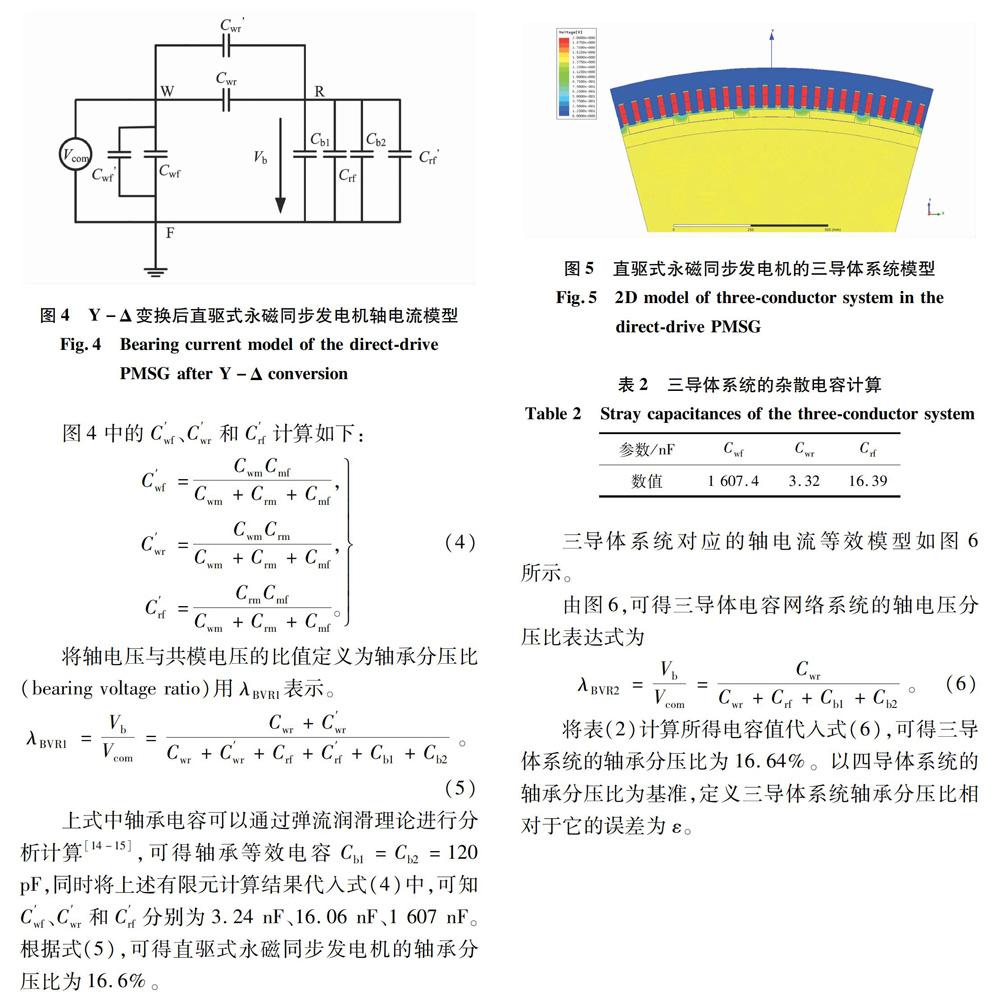
当同步发电机定子采用星形接法时，变流器产生的共模电压Kcom会施加在定子绕组中点与地之间，该电压会经过发电机的电容耦合网络形成共模回路。结合共模电压和电机杂散电容可以得到永磁同步发电机的轴电流分析模型如图3所示。模型中假设电机定子接地良好，忽略了定子机壳到地的接地阻抗。用集中电路的杂散电容表示电机内部耦合网络。设电机轴承润滑良好，轴承内外圈与滚道之间的油膜形成了轴承电容。电机两端的轴承电容存在于转轴和定子机壳之间。

一般而言，变频电动机的轴承分压比在10%内，直驱式永磁同步风力发电机的轴电压大于变频电动机。而双馈风力发电机轴承分压比会达到90%以上，这是由于双馈电机采用了转子侧变流器馈电方式。直驱式永磁同步发电机的轴电压比双馈电机要小很多，轴电流危害也会明显小于双馈异步风力发电机。

1.3直驱式永磁同步发电机电容简化模型

直驱式永磁同步发电机的轴电流分析模型中，电容参数多，轴承分压比计算复杂，也不容易观察出影响轴电压的关键电容参数。为了寻找出关键参数，且不影响轴电压分压比结果，可对初始模型进行化简。

在式（4）和式（5）的轴承分压比中，除轴承电容外，5个杂散电容参与了计算。比较各电容值的大小可知，定子绕组与转子铁心之间的杂散电容cwr（0.11nF）远小于星三角变换后的cwf（3.24nF），转子铁心与定子铁心之间的杂散电容Crf（0.51nF）远小于星三角变换后的Crf（16.06nF）。这说明在计算发电机轴承分压比时，Cwr和Crf对轴承分压比影响并不大。原因在于：1）发电机定子铁心（定子绕组）与转子铁心的之间的间距大，Cwr和crf的数量级较小。2）两者之间存在永磁体且极弧系数较大（75%），一定程度上可以理解为永磁体将定子铁心（定子绕组）与转子铁心完全隔开。

基于上述分析，对四导体系统进行简化：将永磁体与转子铁心之间的粘结剂去掉，将永磁体与转子铁心视为同一导体，则四导体系统转化为三导体系统。对2.1MW直驱永磁同步发电机的杂散电容有限元计算，三导体系统有限元计算电压分布如图5所示，得到电机杂散电容结果如表2所示。

由式（7）可得该误差仅有0.3%。所以将永磁体与转子铁心视为同一电位，将四导体系统简化为三导体系统的方案是可行的。精简了模型，可以突出主要矛盾，便于分析影响轴电压和轴电流的主要参数，同时也可以简化后续电机轴电流的分析预测。

1.4轴承分压比的灵敏度分析

轴承分压比是衡量电机轴承损坏的一个重要指标，分析发电机中各杂散电容与轴承分压比的关系，可以为轴电流的抑制措施提供指导。因此以直驱式永磁同步发电机简化模型的杂散电容为基础，对该发电机的轴承分压比展开灵敏度分析。

由于该发电机的杂散电容Cwf在轴承分压比公式中不体现，轴承等效电容Cb（Cb=120pF）只与轴承电气特性相关。所以针对其他两个杂散电容（即Cwr-Crf）进行分析，研究杂散电容值与轴承分压比之间的关系。

由上图可知：轴承分压比λBVR2随着Cwr的增加而增加，随着crf的增加而减小。当Cwr趋近于1nF时，轴承分压比λRVR2趋近与0。在工程实际中，采取合理的措施，适当地减小定子绕组与转子铁心问的杂散电容Cwr或者增大定子铁心与转子铁心之间的杂散电容crf可以有效地抑制内置式永磁同步风力发电机的轴承分压比，进而抑制轴电流问题。

2变流器一直驱式永磁同步发电机系统轴电流仿真分析

2.1变流器一直驱式永磁同步发电机系统仿真模型

基于永磁同步风力发电机的三导体系统的简化模型，与变流器相结合，得到系统的共模分析模型，其拓扑结构如图8所示。

图8中变流器与永磁同步发电机定子绕组相连接，高频共模电压Vcom存在于定子绕组与地之间，通过电容网络构成共模回路。由定子机壳到地的线路上流过的就是共模电流Icom。图中Ud代表直流母线电压;定子绕组电阻和漏感分别用R、L表示;假设电机外壳良好接地，忽略接地阻抗。cH是轴承等效电容。当轴承两端电压低于轴承阈值电压时，油膜完整，此时轴承等效为电容;当高于轴承阈值电压发生油膜击穿时，轴承两端电压突降，轴承上流过较大的击穿电流，此时轴承等效为电阻Rb。为简化问题，只分析一端轴承的电容击穿过程。等效开关后，和k2用来模拟油膜的击穿过程。分析模型中Ch1=Cb2=120pF，轴承等效电阻Rb=10Ω，轴承等效电容击穿的阈值电压为±15V。

2.2变流器一永磁同步发电机系统的仿真分析

在Matlab/SIMULINK中搭建系统仿真模型，如图9所示。设置直流母线电压Ud为1100V，载波频率为f=5kHz，电机杂散电容采用表（2）中的数值，通过逻辑模块模拟轴承击穿进行仿真分析。分别在定子绕组星形中点和地之间测量共模电压Vcom在轴承内外圈问（即转轴和地之间）测量轴电压Vb，在电机外壳和地之间测量共模电流Icom在轴承支路上测量轴电流，Ib共模电压Vcom共模电流，Icom轴电压Vb以及轴电流，Ib波形如图10所示。

图10可以看出，共模电压呈六阶梯波状。当轴承油膜发生放电击穿时，轴电压与共模电压的比值不再遵循轴承分压比。仿真所得的共模电压Vcom峰值约为570V，共模电流Icom的峰值为150A，轴电压Vb的峰峰值约为15V，轴电流，h的峰峰值也将达到1.3A，该放电电流会使轴承产生坑蚀，严重时会影响整个机组的安全运行。

3直驱式永磁同步发电机轴电流的抑制

轴电流的抑制方法可以从变流器侧着手，如采用多电平变流器、采用能消除共模电压的调制方式;也可以从改变电机耦合通路着手，如改变电机杂散电容参数即静电屏蔽法或转轴电刷接地法;在轴承部件方面采用绝缘轴承或绝缘端盖等方案抑制轴电流。

下面分析改变耦合通路的轴电流抑制措施。由轴承分压比的灵敏度分析可知，采用减小杂散电容Cwr的静电屏蔽法可以有效地降低轴承分压比，进而抑制轴电流;或者采用转轴（通过电刷）直接接地法使轴电压短路。下面分别对这两种抑制方法进行仿真分析，探讨这两种措施对共模电流和轴电流的抑制效果。

设置杂散电容cwr=0.332nF（原来电容值的1/10）来模拟静电屏蔽法;在轴承内外圈问并联小电阻Rb=1Ω来模拟电刷接地法。对上述两种方法分别搭建仿真电路，对共模电压、共模电流、轴电压和轴电流进行计算，并与未抑制时隋况进行对比，结果如表3所示，表中各量为其峰值。

通过表3可知，静电屏蔽法和转轴电刷接地都能大大降低轴电流的幅值，因此都是有效的轴电流抑制措施。但是采取这些措施后共模电流的幅值降低较少。也就是说静电屏蔽法和电刷接地法不能用于抑制共模电流。为抑制共模电流可以采用添加共模扼流圈的方法。

4结论

本文针对直驱式永磁同步风力发电机进行了轴电流的建模、预测和抑制的研究，得到的结论如下：

1）直驱式永磁同步发电机杂散电容网络可以简化为三导体模型，其有效性通过简化前后轴承分压比基本不变得到证明。

2）直驱式永磁同步发电机的轴电压大于变频电动机轴电压，远小于双馈异步发电机的轴电压，其可能产生的轴电流危害也介于两者之间。

3）对变流器一发电机系统进行的轴电流仿真，预测了该系统的轴电流。静电屏蔽和电刷接地两种轴电流抑制措施可以有效地抑制轴电流，但是對共模电流无抑制效果。

目前国内外对兆瓦级风电机组轴电流的实验测量还没有成熟的方法，本文也仅进行了永磁同步发电机轴电流的仿真分析，对其开展实验测量将是今后的一项研究内容。