应急物资运输路径多目标优化模型及求解算法

李卓 李引珍 李文霞

摘 要：针对应急前期运输商自有车辆不足的实际背景，采用自有车辆和第三方租用车辆共同配送的运输模式，对混合车辆路径的组合优化问题进行研究。首先，考虑需求点和运输商的不同利益诉求，以系统满意度最大、系统配送时间和总成本最小为优化目标，建立带软时间窗的多目标混合车辆路径优化模型。其次，考虑NSGA-Ⅱ算法在求解该类问题时收敛性差和Pareto前沿分布不均匀的缺点，将蚁群算法的启发式策略和信息素正反馈机制用于生成子代种群，非支配排序策略模型用于指导算法的多目标择优过程，并引入变邻域下降搜索以扩大搜索空间，提出求解多目标的非支配排序蚁群算法以突破原有算法瓶颈。算例表明：构建的模型可对决策者在不同的情境下依据不同的优化目标选择合理的路径提供参考，提出的算法在求解不同规模的问题和不同分布类型的问题中均表现出较好的性能。

关键词：应急物流;混合车辆路径问题;多准则优化;非支配排序策略;蚁群算法;变邻域搜索

中图分类号：TP301.6

文献标志码：A

Multi-objective optimization model and solution algorithm for emergency material transportation path

LI Zhuo， LI Yinzhen*， LI Wenxia

School of Traffic and Transportation，  Lanzhou Jiaotong University， Lanzhou Gansu 730070， China

Abstract：

For the actual background of the shortage of self-owned vehicles of the transporters in the early stage of emergency， the combinatorial optimization problem of hybrid vehicle paths with transportation mode of joint distribution of self-owned vehicles and  vehicles rented by third-party was studied. Firstly， with the different interests between demand points and transporters considered， a multi-objective hybrid vehicle routing optimization model with soft time windows was established with the goal of maximizing system satisfaction and minimizing system delivery time and total cost. Secondly， the shortcomings of NSGA-Ⅱ algorithm in solving this kind of problems such as poor convergence and uneven distribution of Pareto frontiers were considered， the heuristic strategy and pheromone positive feedback mechanism of ant colony algorithm were used to generate offspring population， non-dominated sorting strategy model was used to guide the multi-objective optimization process， and the variable neighborhood descent search was introduced to expand the search space. A multi-objective non-dominated sorting ant colony algorithm was proposed to break through the bottleneck of the original algorithm. The example shows that the proposed model can provide reference for decision makers to choose reasonable paths according to different optimization objectives in different situations， and the proposed algorithm shows better performance in solving different scale problems and different distribution type problems.

Key words：

emergency logistics; heterogeneous vehicle routing problem; multi-criteria optimization; non-dominated sorting strategy; ant colony algorithm; variable neighborhood search

0 引言

隨着全球自然环境的急剧变化，一系列突发事件给社会稳定和安全带来严重威胁，然而国内由于应急物流体系不够完善，造成的损失占其总损失的15%～20%[1]。因此，建立完善的应急系统已成为热点议题，对缓解灾情、降低损失具有重要意义。

应急物流体系是一个多阶段、多层次结构的供应网络。针对末端配送的车辆路径问题（Vehicle Routing Problem， VRP），国内外学者展开了广泛研究[2-4]。关于单目标的应急VRP问题，郭咏梅等[5]考虑路网通行能力和物资优先级，以系统响应能力最大为目标构建开放式车辆路径问题（Open Vehicle Routing Problem， OVRP）数学模型，并设计改进蚁群算法进行求解。程碧荣等[6]针对物资供应不足及需求不确定的特点，提出随机需求环境下的应急路径优化方法。Wohlgemuth等[7]最小化时间延误并提高车辆利用率，建立了确定性需求下的动态车辆路径优化模型。关于多目标的应急VRP问题，多数文献通常考虑时效性和经济性[8-9]。近年来，随着研究的深入，部分学者兼顾考虑需求点的需求满足率和救援公平性等，如Chang等[10]提出最小化交付时间、运输成本和需求不满足率的三目标优化模型，并针对该问题设计基于贪婪搜索的多目标遗传算法。Zhang等[11]最大限度降低需求未满足程度、总交付时间和配送的不平衡性，提出多目标、多周期的应急物流优化方法。由于VRP问题的NP-hard性质，精确算法无法避免指数爆炸问题，难以求解大规模问题[12]，而遗传算法、蚁群算法、禁忌搜索算法等启发式算法在解决该类问题中表现出良好的求解效果[13-15]，但在求解精度和收敛性等方面仍有待提高，为此，已有学者考虑对算法进行改进[16-17]。综上所述，既有研究中大多数文献针对的实际背景问题较为单一，采用多目标优化模型且设计更有效的求解算法的文献比较少见。

在实际救援中，由于突发事件的随机发生，造成救援初期可调度的应急设施往往不能应付繁重的救援工作，尤其是面对大规模、多灾点的应急物资运输任务，运输车保有量不足使得可调度的车辆有限，必然会降低救援效率，造成额外的经济损失和人员伤亡。为此，本文考虑应急前期自有车辆不足的一类实际情况，提出自有车辆和租用车辆相结合的配送模式，即混合车辆路径问题。混合性概念涉及车辆所有权，即应急初期配送车辆数不足时，必须从第三方承运人租用车辆完成配送。基于此，考虑灾点系统满意度、运输总成本和系统配送时间建立多目标应急路径优化模型，并针对该问题设计求解多目标的非支配排序蚁群算法。

1 多目标优化模型

1.1 问题描述

某些突发事件波及范围较大，且末端物资运输工作具有时间的紧迫性和面向多灾点的复杂性，导致运输商自有车辆不足，需要租借车辆继续完成配送任务。考虑车辆的所有权，自有车辆完成配送任务后需返回调度中心，是闭环VRP;租用车辆完成配送任务后停留在最后一个任务点，不需返回调度中心，是开环VRP。基于此，该问题可归结为带软时间窗的混合车辆路径问题（Heterogeneous Vehicle Routing Problem with Soft Time Windows， HVRPSTW），如图1所示。本文以此为背景，从实际角度出发，解决应急条件下兼顾多个优化方面的运输路径选择问题，设计建立多目标优化数学模型。

1.2 模型参数及变量

完全有向的应急物流运输网络为G=（V，E），其他参数及相关变量见表1。

1.3 HVRPSTW模型建立

灾后需求点对时效性的要求较高，在尽可能满足需求点时间窗限制的前提下，随着交付时间的延迟，满意度逐渐降低，满意度按下式计算：

wki=（li-tki）/li， 0≤tki≤li

0，tki>li（1）

考虑取所有需求点满意度的平均值为系统满意度S：

S=1n-1∑i∈V0∑k∈Kykiwki（2）

为了加快设备周转速度，运输企业需要考虑系统配送时间，这里，首先定义第k类车第mk辆车完成若干需求点配送任务所花费的时间Tmk：

Tmk=∑i∈V∑j∈Vxkijtkij+∑i∈V0ykiui-∑i∈V0xbi0tbi0; k∈K（3）

完成所有需求点配送任务的系统配送时间T为：

T=max{Tmkk∈K}（4）

此外，还要考虑经济性，总配送费用为：

C=∑i∈V∑j∈V∑k∈Kxkijfij+∑j∈V0∑k∈Kxk0jfrk-∑i∈V0xbi0fi0+∑i∈V0∑k∈Kykipi（tki）（5）

其中：pi（tki）=r·max{（tki-li），0}为超出时间窗限制的惩罚成本函数。

表格（有表名）

表1 模型变量参数定义

Tab. 1 Variables and parameters definition of model

类型符号含义

集合参数变量

V节点集合，V={1，2，…，n}，调度中心为1

V0需求点集合，V0=V/{1}

E节点间有向弧段集合E={（i， j）：i， j∈V，i≠j}

A需求點的任意子集，AV0

K车辆类别集合，K={k|a，b}，k=a为自有车，k=b为租用车

mkk类车辆集合，mk={1，2，…，n}

vkk类车平均速度

Qkk类车载重

qi需求点i的物资需求量

ui需求点i的服务持续时间

tu单位需求量的服务时间

diji≠j∈V间路径（i， j）∈E的长度

fij路径dij的行驶成本

frkk类车固定启用成本

tkijk类车在路径dij的行驶时间

li需求点i时间窗上界

c路径dij的单位行驶成本

r超出时间窗li限制单位时间惩罚成本

M控制参数，极大整数

tkik类车到达需求点的时间，tk 0=0

xkij决策变量，当k类车负责路径（i， j）∈E时取值为1;否则为0

yki决策变量，当k类车服务需求点i∈V0时取值为1;否则为0

考虑运输过程的复杂性，兼顾多个优化方面，建立多目标路径优化模型：

Z=（FS（y），FT（x，y），FC（x，y））（6）

FS（y）=max S（7）

FT（x，y）=min T（8）

FC（x，y）=min C（9）

s.t. ∑j∈V∑k∈Kxkij=∑j∈V∑k∈Kxkji=1; i∈V（10）

∑i∈V∑j∈Vxkij≤A-1; k∈K，A≥2（11）

∑j∈V0xk0j=∑j∈V0xkj0≤mk; k∈K（12）

∑i∈Vxkih-∑j∈Vxkhj=0; k∈K，h∈V0（13）

∑i∈V0ykiqi≤Qk; k∈K（14）

tki+ui+tkij≤tkj+M（1-xkij）; i， j∈V0，k∈K（15）

tkij=dij/vk

fij=c·dij

ui=tu·qi ;i， j∈V， k∈K（16）

xkij，yki∈{0，1}; i， j∈V，k∈K（17）

Qk，qi，ui>0; i∈V0，k∈K（18）

模型中，式（6）～（9）为多运输准则的不同优化目标;式（10）保证每个需求点仅被一辆车服务且仅服务一次;式（11）为子回路消除约束;式（12）保证车辆从调度中心出发最后返回调度中心，且启用车辆数小于车辆拥有数;式（13）为节点平衡方程;式（14）为车辆载重约束;式（15）为配送过程中各需求点的时间限制条件;式（16）～（18）为决策变量和参数约束。

2 求解算法设计

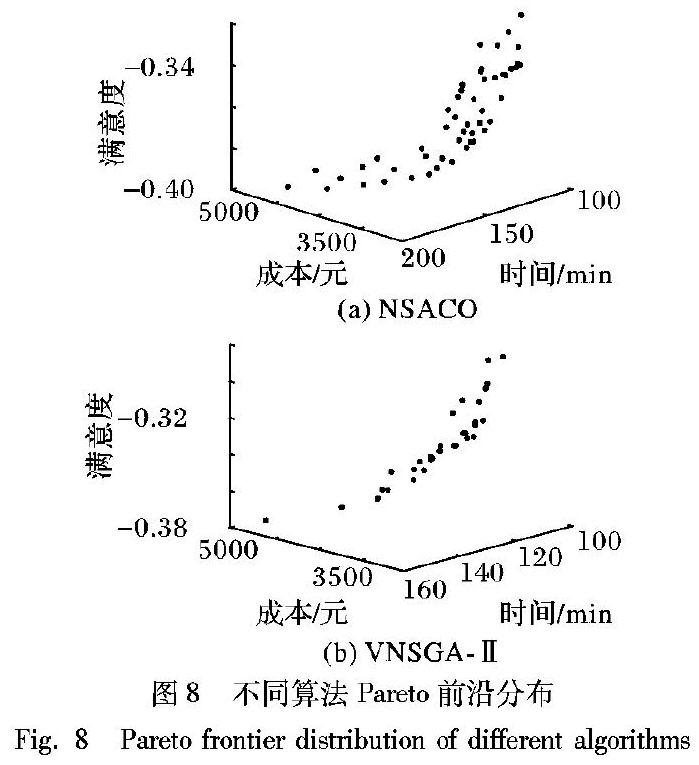
HVRPSTW是VRP问题的变体之一，启发式算法是解决该类问题的有效方法之一。蚁群优化（Ant Colony Optimization， ACO）算法在求解VRP及其变体中得到了成功的应用，在求解大规模问题中表现出较好的收敛性[18];改进非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm-Ⅱ， NSGA-Ⅱ）作为常用的多目标求解算法，比同类算法表现出更优的性能[19]。考虑上述两种算法的优势，首先以ACO算法为基本架构，非支配排序策略用于多目标择优过程;其次，为了避免算法在迭代后期陷入信息素停滞，采用变邻域下降搜索机制，进一步扩大搜索的解空间。设计求解多目标的非支配排序蚁群优化算法（Non-dominated Sorting-Ant Colony Optimization algorithm， NSACO）。

2.1 求解多目标的NSACO算法

2.1.1 非支配排序策略模型

模型包括两个子过程：非支配排序和拥挤度评估。非支配排序是对种群进行非支配前沿划分，保证相同排序层级个体之间不存在支配关系;拥挤度是同一排序层个体周围的个体密度，确保种群多样性。

构建初始种群P，计算适应度值并基于Pareto占优对P分层排序为k层子集，即P={P1，P2，…，Pk}，Pi+1中个体受Pi中个体支配，且Pi∩Pi+1=，i，i+1∈{1，2，…，k}，得到种群个体间的非支配关系。对于个体p∈P初始化两个参数np和sp，np记录支配个体p的个体数量，sp存放被个体p支配的个体的集合。执行以上非支配排序过程后，计算每个排序层Pi中个体p的拥挤程度I（p），p∈Pi，拥挤度I是相同排序层中相邻个体适应度fh（x）的距离差值。

执行以上两个子过程后，种群P中个体p被赋予非支配排序层级prank和拥挤度I（p），通过以上两个属性区分个体间的优劣关系：满足①prankI（q）;则个体p优于q。

2.1.2 变邻域下降搜索

在经过规定的迭代次数后，解的质量仍然没有改善，则启

用变邻域下降搜索。该过程采用多个不同邻域进行系统搜索，首先采用小邻域结构，当解没有改进时，再切换较大的邻域结构。变邻域下降搜索伪代码如下。

程序前

for each p∈parent_set

Select a neighbourhood structure VLSi， i=1，2，…，imax

i → 1//初始化邻域结构VLS1

While i ≠ imax+1

VLSi（p）→p′//对p执行邻域结构VLSi

If p′ unfeasible

repair p′//修复不可行解

If （f（p′）

p′ → p， i → 1//更新當前可行解

else

i=i+1

end

If（f（p）

p→p*//更新全局最优解

end

程序后

本文采用4个邻域结构（VNS={VNS1，VNS2，…，VNS4}）的搜索机制;两个子路径内邻域结构，两个子路径间邻域结构具体如下：

子路径内relocate算子（VNS1）：随机选取路径1-11-5-1-6-2-4-7-3-1-16-14-8-1中一条子路径1-6-2-4-7-3-1，对子路径随机生成移出节点note1和插入节点note2，将note1位置对应的元素插入到note2位置，如图2。

子路径内or-opt算子（VNS2）：随机选取路径1-11-5-1-6-2-4-7-3-1-16-14-8-1中一条子路径1-6-2-4-7-3-1，对子路径随机选择两个移出节点note1、note2间的路径序列sq，随机选择一个插入节点note3，sq从原位置移出，插入到新的位置，如图3。

子路径间relocate算子（VNS3）：针对一条路径1-6-2-4-1-7-3-8-10-1，随机生成移出节点note1和插入节点note2，将note1位置对应的元素插入到note2位置，如图4。

子路径间or-opt算子（VNS4）：针对一条路径1-6-2-4-1-7-3-8-10-1，随机选择两个移出节点note1、note2间的路径序列sq，随机选择一个插入节点note3，sq从原位置移出，插入到新的位置，如图5。

要注意的是，执行子路径内的邻域结构不会破坏解的可行性，执行子路径间的邻域结构有可能会破坏解的可行性，即有可能会违背车辆容量约束，因此，需要检查所得解是否可行，若不满足可行性，对解进行修复。

2.1.3 算法流程

算法迭代过程中，通过蚁群算法中的路径启发式信息和路徑信息素浓度反馈机制生成子代种群Pc，与父代种群Pp相结合生成本次迭代的种群集合P;对P执行非支配排序并评估拥挤度，基于个体排序层rank和拥挤度I执行精英保留策略，得到下一迭代的父代种群Pp;基于Pp进行路径信息素浓度更新，为产生下一子代做准备;当执行指定迭代次数后，所得可行解没有改进，则执行变邻域下降搜索扩大搜索解空间，以期改善解的多样性。不断循环以上过程，直到满足算法停止条件，算法流程如图6所示。

2.1.4 算法主要环节

1）初始化可行解。车辆路径采用自然数编码，以距离当前需求点里程最小为元启发式策略，从未访问点集合中搜索下一要访问的需求点，采用基于贪心策略的调度中心插入方法，若车辆当前载重与下一将要访问需求点的需求量之和违背车辆载重约束，则将调度中心编号插入，表明需要另一辆车完成后续配送任务，以此生成质量较高的初始解集P0。

2）生成父代。基于Pareto占优执行非支配排序策略模型，给种群P中每个个体p赋予排序层prank和拥挤度I（p）两个属性，用于执行精英保留策略，通过择优产生下一代的父代种群。

3）全局信息素更新。考虑多目标的不同量纲对信息素浓度更新结果的影响，对父代个体的每个适应度值进行无量纲化处理后，路径（i， j）的信息素浓度更新规则为：

τij（t+1）=（1-ρ）τij（t）+∑Hh=1Δτhij（19）

Δτhij=Q/fh（p）， （i， j）∈p

0，（i， j）p（20）

其中：H为目标数; fh（p）为个体p第h个目标无量纲化后的适应度值。

4）生成子代。依据路径（i， j）的启发式信息ηij和信息素浓度τij计算未访问需求点的转移概率Psij，轮盘赌选择确定下一访问点，同时保证满足车辆载重约束。采用同样的方式依次生成子代种群所有个体。路径（i， j）的选择概率为：

Psi， j（t）=τij（t）α·ηij（t）β∑k∈Asτik（t）α·ηik（t）β， j∈Ak

0，jAk（21）

3 数值实验及分析

3.1 基础算例实验

随机生成20个节点，包含1个应急调度中心和19个物资需求点。本算例设置节点1为调度中心，其他各需求点的需求量（吨）是区间[0，10]均匀分布的随机整数，需求点时间窗（min）在区间[0，60]中随机产生，违背时间窗单位惩罚成本为4元/min，需求点的服务持续时间为2min/t;运输商拥有2辆载重为25t的自有车，行驶速度v1=1.2km/min，启用成本为每辆300元;租用车载重为15t，车辆数充足，行驶速度v2=1.5km/min，启用成本为每辆200元/辆;配送过程中单位运输成本为5元/km;具体见表2。

采用本文提出的NSACO算法对算例进行200次迭代求解。设置种群规模pop=50，最大迭代次数gen=200，允许可行解没有改进的最大迭代次数noimpro=10;蚁群优化参数参考文献[18]进行设置，α=1， β=5， ρ=0.2;算法在一台搭载1.6GHz的Intel Core i5处理器和4GB内存的计算机平台上实现。各目标最优时的车辆路径如图7所示，各目标最优时的非支配路径集合和路径属性见表3。

运输商和需求点对应急物资运输路径的要求不同，相应的优化目标并不统一，使各目标同时达到最优的解不存在。由表3和图7可知：当FC（x，y）取最优时，车辆组合为2a+2b，平均满载率为81.00%，配送路径如图7（a），FT（x，y）比F*T（x，y）增加15.42%，FS（y）比F*S（y）降低17.53%;当FT（x，y）取最优时，车辆组合为2a+2b，平均满载率为83.67%，配送路径如图7（b），FC（x，y）比F*（x，y）增加9.51%，FS（y）比F*S（y）降低16.96%;当FS（y）取最优时，车辆组合为2a+2b，平均满载率为82.33%，配送路径如图7（c），FC（x，y）比F*C（x，y）增加29.82%，FT（x，y）比F*T（x，y）增加53.71%。从企业角度考虑，需提高效益，加快设备周转，为此，合理规划路径的同时，减少启用车辆数，提高车辆满载率，以期降低成本、减少系统配送时间;从需求点角度考虑，在尽量控制成本的基础上，科学安排配送顺序，以期满足物资能尽早送达的要求。基于以上分析，在不同的实际情境下，决策者可根据不同目标偏好选择配送路线;若在不同目标之间适当妥协，则即能避免部分目标取较劣值，又可兼顾多个方面。

3.2 算法性能分析

3.2.1 基础算例分析

NSGA-Ⅱ算法作为较为广泛应用的多目标求解算法，吸引了大批学者的关注，近几年来，已有不少针对该算法的改进算法，因此，本文拟将NSACO算法与Hassanzadeh等[20]于2017年提出的VNSGA-Ⅱ進行比较。以基础算例为实验数据，设置交叉概率为0.9，变异概率为0.1，其他实验条件及参数相同，NSACO与VNSGA-Ⅱ分别执行10次算法程序，对二者计算结果进行分析。为了便于比较，取系统满意度的相反数统一各目标优化方向，生成的Pareto前沿空间分布见图8，算法性能统计见表4。

比较图8（a）和图8（b）看出，NSACO算法得到的Pareto前沿中，Pareto最优解的数量更多，重复数据点较少，Pareto前沿跨度更广且空间分布均匀性更好，说明算法具有较强的搜索性能，可以搜索更大的解空间。由表4可知，NSACO在算法性能上总体比VNSGA-Ⅱ更好。具体从以下三个方面分析：求解精度上，尽管NSACO求得的总成本在最优解和平均解上分别比VNSGA-Ⅱ大0.48%和0.35%，但NSACO求得系统配送时间和系统满意度均比VNSGA-Ⅱ更优，系统配送时间的最优解和平均解分别优化了3.00%和4.51%，系统满意度的最优解和平均解分别优化了8.30%和7.42%。收敛性上，由于ACO算法的信息素正反馈机制，相较于VNSGA-Ⅱ的随机搜索，NSACO在三个目标上分别提前了56、34、27个迭代循环，收敛性明显优于VNSGA-Ⅱ。算法稳健性上，在三个优化目标上，NSACO的平均偏差分别为2.60%、1.76%、2.75%，最大偏差分别为3.43%、2.48%、4.98%;VNSGA-Ⅱ的平均偏差分别为2.39%、3.38%、1.95%，最大偏差分别为6.08%、5.48%、4.06%;表现出较好的稳健性。由于NSACO算法在迭代过程中需要额外更新路径的信息素浓度，算法运行时间相对较长。

3.2.2 测试算例分析

为了验证提出算法在求解VRP问题的普适性，采用Solomon基准算例对算法性能作进一步测试分析，本文选取C101、R101、RC101三组不同类别的算例作为测试数据，分别对NSACO算法与VNSGA-Ⅱ算法运行10次，算法参数及实验条件与基础算例相同，测试结果如表5所示。

由表4和表5可知，在小规模基础算例实验中，仅时间和

满意度在精度方面得到了改进，而在大规模实例中，由于蚁群优化

的信息素正反馈机制及轮盘赌选择策略，使得NSACO算法相较于VNSGA-Ⅱ算法在三个优化目标的精度上均有提高，并且在不同类型实例的求解中均表现出优势。分析NSACO在成本、时间、满意度三个方面的改进程度，聚集分布实例C101在最优解上分别优化了4.08%、4.52%、2.90%，在平均解上分别优化了6.80%、5.17%、4.02%;随机分布实例R101在最优解上分别优化了10.59%、8.99%、2.96%，在平均解上分别优化了12.92%、8.79%、5.31%;混合分布实例RC101在最优解上分别优化了9.68%、9.47%、2.78%，在平均解上分别优化了11.97%、10.10%、4.81%。由此可见，相较于聚集分布问题，NSACO在解决随机分布问题和混合分布的问题更能发挥其算法优势，具有更好的可行性和精确性。

4 结语

本文以应急初期自有车和租用车混合配送为实际背景，建立多目标HVRPSTW优化模型，针对该问题设计了求解多目标的NSACO算法。通过基础算例和测试算例对模型和算法进行验证，结果表明：

1）针对应急物资运输中企业私有车辆不足的一类情况，对同一路网内自有车和租用车共同完成配送的组合优化问题进行了研究，对该实际背景下的配送路径规划工作具有很强借鉴意义。

2）模型考虑总成本、系统配送时间和系统满意度三个方面，有效地平衡受灾点和运输企业双方的利益，具有很强的实用性，可以给运输商在不同的应急背景下根据不同优化目标选择合理的运输路径提供决策依据。

3）设计NSACO算法求解模型，与改进VNSGA-Ⅱ算法相比，NSACO能快速搜索到最优解，并改善Pareto前沿的分布均匀性。算例分析表明：NSACO算法在求解精度、收敛性及稳健性上均表现出更好的性能。

本文仅从静态路网的角度对应急路径的优化作研究，而更符合实际的时间依赖性车辆路径以及动态车辆路径将是下一步研究课题。

参考文献

[1]何明珂.应急物流的成本损失无处不在[J].中国物流与采购，2003（23）：18-19.（HE M K. The cost loss of emergency logistics is ubiquitous[J]. China Logistics and Purchasing， 2003（23）：18-19.）

[2]王付宇，王涛，叶春明.突发灾害事件情景下应急救援车辆调度问题综述[J].计算机应用研究，2017，34（10）：2887-2891.（WANG F Y， WANG T， YE C M. Review of emergency rescue vehicle scheduling problem under sudden disaster [J]. Application Research of Computers， 2017， 34（10）： 2887-2891.）

[3]曹琦，曹阳.应急物资配送车辆调度模型与优化综述[J]. 计算机应用， 2018，38（8）：2416-2422.（CAO Q， CAO Y. Review of model and optimization of vehicle scheduling for emergency material distribution [J]. Journal of Computer Applications， 2018， 38（8）： 2416-2422.）

[4]ARDEKANI S A，HOBEIKA A G. Logistics problems in the aftermath of the 1985 Mexico city earth-quake[J]. Transportation Quarterly， 1988， 42（1）： 107-124.

[5]郭咏梅，胡大伟，陈翔.改进蚁群算法求解带时间窗的应急物流开环车辆路径问题[J].长安大学学报（自然科学版），2017，37（6）：105-112.（GUO Y M， HU D W， CHEN X. Solution of emergency logistics open-loop vehicle routing problem with time window based on improved ant colony algorithm [J]. Journal of Changan University （Natural Science Edition）， 2017， 37（6）： 105-112.）

[6]程碧荣，赵晓波，秦进.考虑供应不足的应急物流车辆路径优化模型及算法[J].计算机应用研究，2016，33（6）：1682-1685.（CHENG B R， ZHAO X B， QIN J. Optimization model and algorithm for emergency vehicle route with insufficiency supply [J]. Application Research of Computers， 2016， 33（6）： 1682-1685.）

[7]WOHLGEMUTH S， OLORUNTOBA R， CLAUSEN U. Dynamic vehicle routing with anticipation in disaster relief [J]. Socio-Economic Planning Sciences， 2012， 46（4）： 261-271.

[8]NOROUZI N， SADEGH-AMALNICK M， TAVAKKOLI-MOGHADDAM R. Modified particle swarm optimization in a time-dependent vehicle routing problem： minimizing fuel consumption [J]. Optimization Letters， 2016， 11（1）： 121-134.

[9]杜苗苗.基于應急物资分类—分批配送的应急车辆路径研究[D]. 北京：北京交通大学，2014： 27-36.（DU M M. Emergency vehicle routing problem research based on emergency relief classification-batches distribution [D]. Beijing： Beijing Jiaotong University， 2014： 27-36.）

[10]CHANG F， WU J， LEE C， et al. Greedy-search-based multi-objective genetic algorithm for emergency logistics scheduling [J]. Expert Systems with Applications， 2014， 41（6）： 2947-2956.

[11]ZHANG J， PENG J， XU Z， et al. SDVRP model for emergency logistics and evolutionary heuristic approach [C]// Proceedings of the 2013 International Conference on Automatic Control and Artificial Intelligence. Stevenage， UK： IET， 2013： 1809-1812.

[12]方金城，张岐山. 物流配送车辆路径问题（VRP）算法综述[J]. 沈阳工程学院学报（自然科学版）， 2006， 2（4）： 357-360.（FANG J C， ZHANG Q S. Algorithm review on vehicle routing problem in logistics distribution [J]. Journal of Shenyang Institute of Engineering （Natural Science）， 2006， 2（4）： 357-360.）

[13]da COSTA P R O， MAUCERI S， CARROLL P， et al. A genetic algorithm for a green vehicle routing problem [J]. Electronic Notes in Discrete Mathematics， 2018， 64： 65-74.

[14]STODOLA P， MAZAL J， PODHOREC M， et al. Using the ant colony optimization algorithm for the capacitated vehicle routing problem [C]// Proceedings of the 16th International Conference on Mechatronics—Mechatronika. Piscataway， NJ： IEEE， 2014： 503-510.

[15]BRANDO J. A tabu search algorithm for the heterogeneous fixed fleet vehicle routing problem [J]. Computers and Operations Research， 2011， 38（1）： 140-151.

[16]GOEL R， MAINI R. A Hybrid of Ant colony and Firefly Algorithms （HAFA） for solving vehicle routing problems [J]. Journal of Computational Science， 2018， 25： 28-37.

[17]KAABACHI I， JRIJI D， KRICHEN S. An improved ant colony optimization for green multi-depot vehicle routing problem with time windows[C]// Proceedings of the 18th IEEE/ACIS International Conference on Software Engineering， Artificial Intelligence， Networking and Parallel/Distributed Computing. Piscataway， NJ： IEEE， 2017： 339-344.

[18]萬旭，林健良，杨晓伟.改进的最大最小蚂蚁算法在有时间窗车辆路径问题中的应用[J].计算机集成制造系统，2005，11（4）：572-576.（WAN X， LIN J L， YANG X W. Improved MMAS for vehicle routing problem with time window [J]. Computer Integrated Manufacturing Systems， 2005， 11（4）： 572-576.）

[19]DEB K， PRATAP A， AGARWAL S， et al. A fast and elitist multiobjective genetic algorithm： NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation， 2002， 6（2）： 182-197.

[20]HASSANZADEH A， RASTI-BARZOKI M. Minimizing total resource consumption and total tardiness penalty in a resource allocation supply chain scheduling and vehicle routing problem [J]. Applied Soft Computing， 2017， 58： 307-323.

LI Zhuo， born in 1993， M. S. candidate. His research interests include transportation planning and management， network optimization.

LI Yinzhen， born in 1963， Ph. D.， professor. His research interests include transportation system analysis and decision-making.

LI Wenxia， born in 1993， M. S. candidate. Her research interests include operation management and decision optimization of rail transit， network optimization.