高强度螺栓拉伸紧固试验研究
文 | 王洪波,杨少华,任俊祺,卢晟
大型风电机组的关键部位大多采用高强度螺栓联接,为保证联接的质量,需采用可靠的紧固工艺。拉伸法是通过拉伸工具直接将螺栓(一般使用双头螺柱)拉长产生夹紧力,由于紧固过程中只有轴向拉伸,没有扭转运动并且不需要考虑摩擦的影响,拉伸力更容易得到控制。因此,拉伸法越来越多地应用于风电机组关键部位联接。
根据拉伸工艺特点,为了获得目标预紧力,螺栓拉伸时,需要有一定的“超拉”,即预拉力要大于螺栓的目标预紧力,才能保证卸压后回弹到目标预紧力,但目前行业通常根据工程经验进行预拉力的确定,存在一定局限性。
工程经验认为,预拉力F和目标预紧力F0(在此定义预拉力F和目标预紧力F0的比值为“超拉系数”)需要满足以下关系式:
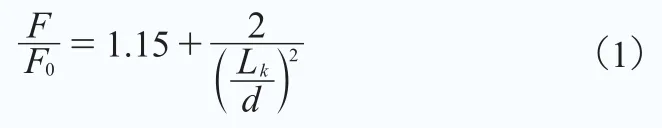
式中,Lk为螺栓的有效拉伸长度,d为螺栓的公称直径。可见,变量仅考虑了螺栓长度、直径等因素,而拉伸法因其先拉伸后卸压回弹的工艺特点,不同工况的螺栓目标预紧力及回弹量可能受到预拉力、拉伸次数、时效性等因素影响,因此,本文采用应变法定量测试某大型风电机组的螺栓拉伸工艺,为制定合理的螺栓拉伸紧固工艺提供依据。
试验过程
设计螺栓拉伸试验工装模拟实际工况,通过拉伸器对20组螺栓施加载荷,采用应变法对某大型风电机组的高强度螺栓M36×345拉伸紧固时的应变量进行测量,记录不同拉伸载荷下应变量的变化,图1为拉伸应变测试示意图。
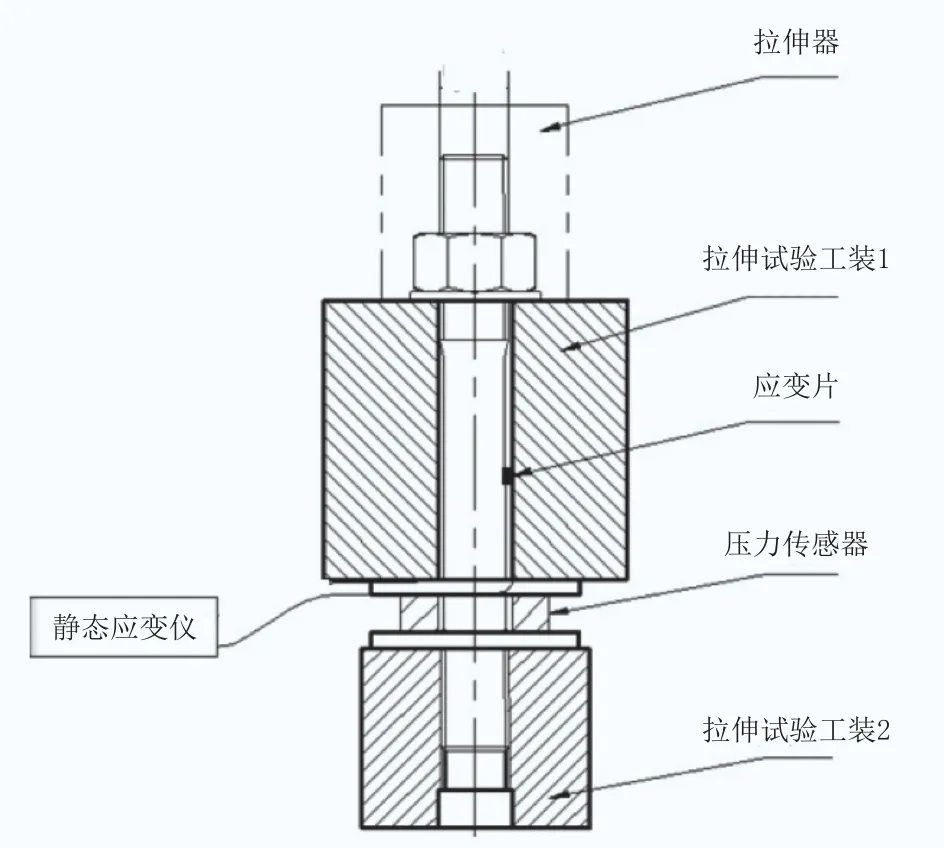
图1 拉伸测试示意图
一、试验原理
将应变片粘贴在试件表面,接入测量电路,随着试件受力变形,应变片的敏感栅也随之变形,致使其电阻值发生变化。此电阻值的变化与构件表面应变成比例,应变片电阻变化产生的信号经电路放大后,由指示仪记录。通过对电学量的分析,即可得出试件力学量的变化,如图2所示。试验所用仪器设备如表1所示。

图2 应变测量原理
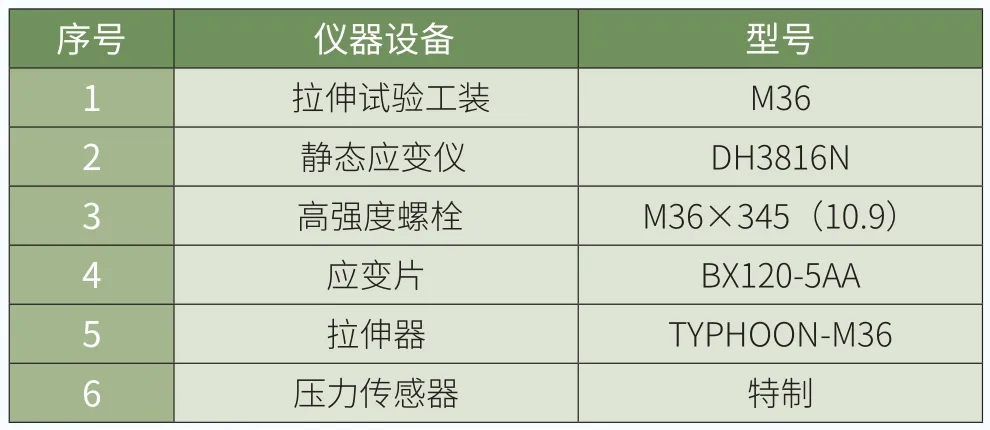
表1 仪器设备及型号
二、试验方案
根据某大型风电机组的螺栓环形分布情况,本次试验共设置20组(总量的1/4)螺栓拉伸试验,具体步骤为:(1)在螺栓的1/2处粘贴应变片,打磨沿螺栓轴线45°方向交叉进行,打磨至粘贴面呈细密、均匀的交叉网纹状,粗糙度满足Ra6.4要求。(2)用502胶将应变片粘贴在螺栓试件表面,将应变片的两根引线与外接导线焊接,并对螺栓试件进行编号。(3)连接应变片、静态应变仪和计算机,输入各测点的电阻值、灵敏系数。(4)采样前对螺栓试件进行3次预加载,以消除初始加载时的误差,预加载荷产生的应变约为1000μm/m。(5)开始采集数据,加载过程分6级,从100kN开始,每级增加100kN,加载至600kN,记录并保存不同载荷及时效下每个测点的数据。(6)测量完毕后,关闭电源。依次拆除应变片、静态应变仪和计算机的数据线,清点仪器和配件。
结果分析
一、与VDI2230标准计算对比
采用行业认可的《VDI2230高强度螺栓连接系统计算》标准,计算拉伸工况下螺栓的应变,并与试验值进行对比,以验证试验的准确性。
螺栓在拉伸紧固时发生弹性变形,根据胡克定律:

式中,F为预拉力,即拉伸器的拉伸载荷;K为螺栓刚度;ε为螺栓应变。
将式(2)进行变换可得:

模拟实际工况,螺栓安装尺寸如图3所示。
根据VDI2230标准5.1.1章的公式:

式中,δs为整个螺栓的柔度,δGM1为基体旋合段柔度,δ1为光杆段柔度,δGew为螺纹未旋段柔度,δGM2为拉伸器旋合段柔度。
上式第一项δGM1为δG1与δM1的加和。
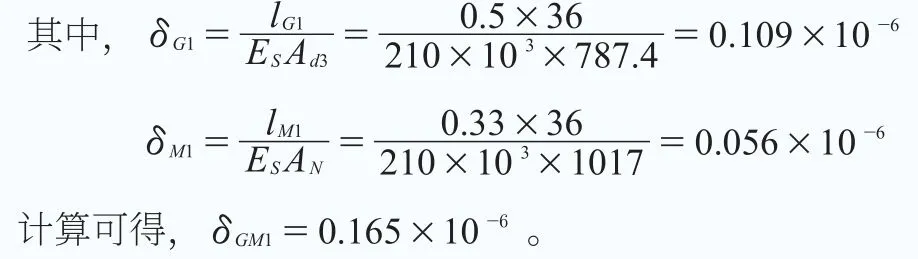
公式(4)其他三项的计算结果:
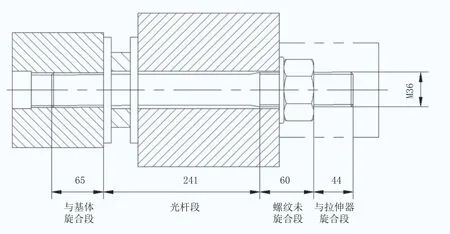
图3 螺栓安装尺寸
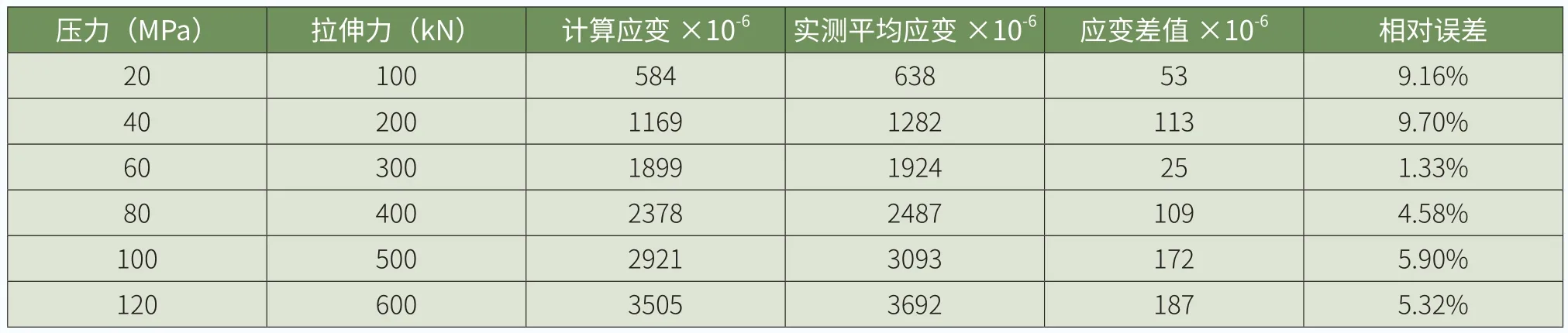
表2 VDI2230标准计算应变与实测平均应变对比

拉伸器压力由20MPa逐级加载至120MPa过程中计算的理论应变与20组螺栓实测的平均应变如表2所示。
由上述统计结果可知,与VDI2230标准计算应变相比,实测值平均应变量的最大相对误差为9.7%,最小相对误差为1.33%。考虑拉伸器精度误差±3%、读数精度误差±3%等影响,采用应变法所测结果最大相对误差约3.7%,试验测量结果可靠。
二、与经验公式超拉系数对比
对螺栓进行拉伸紧固时,施加的载荷不能超过螺栓材料的屈服强度(10.9级的M36×345螺栓保证载荷为678kN)。因此,对螺栓施加678kN拉伸载荷,测量螺栓在拉伸工步和泄压工步下的应变量。将拉伸工步的应变命名为拉伸应变ε1,将泄压工步的应变命名为剩余应变ε2,那么,超拉系数的计算如下式所示:
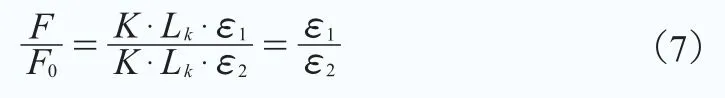
取20组螺栓的应变平均值,测量结果如表3所示。根据经验公式(1)计算超拉系数,结果如表4所示。
由上述结果可知,超拉系数的经验值为1.170,相对实测值1.281小8.6%。因此,如按经验公式设置预拉力,将导致目标预紧力小8.6%,如再考虑拉伸器精度误差±3%、读数误差±3%以及不同螺栓超拉回弹偏差等,累计误差将超过VDI2230标准设计计算所给的拉伸法离散度要求±16%。因此,在制定螺栓拉伸紧固工艺时,应进行试验测量,并以试验测量值为准。

表3 超拉系数的试验值

表4 超拉系数的经验值
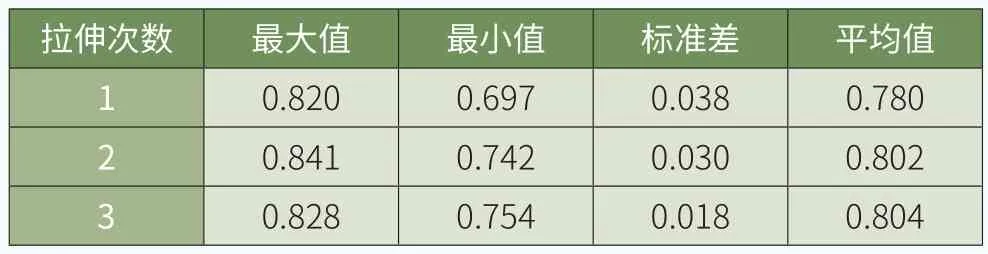
表5 拉伸次数对载荷剩余比的影响
三、螺栓剩余载荷的影响因素分析
分析螺栓拉伸应变测试结果可知,螺栓拉伸-卸压后的剩余载荷还受到拉伸力大小、拉伸次数和时效作用的影响,具体分析见下文。为便于表述,在此定义剩余应变ε2与拉伸应变ε1的比值为螺栓载荷剩余比:

式中,ω为螺栓载荷剩余比。
(一)拉伸力对螺栓载荷剩余比的影响
拉伸器拉力由100kN逐级加载至600kN的过程中,拉伸力与螺栓载荷剩余比关系如图4所示。
由图4可知,随着拉伸力的逐渐增大,M36×345螺栓载荷剩余比逐渐增大并趋于稳定值0.8,即相同工况条件下,随着拉伸力的增大,螺栓超拉系数会随预紧力的增加而逐渐变小。
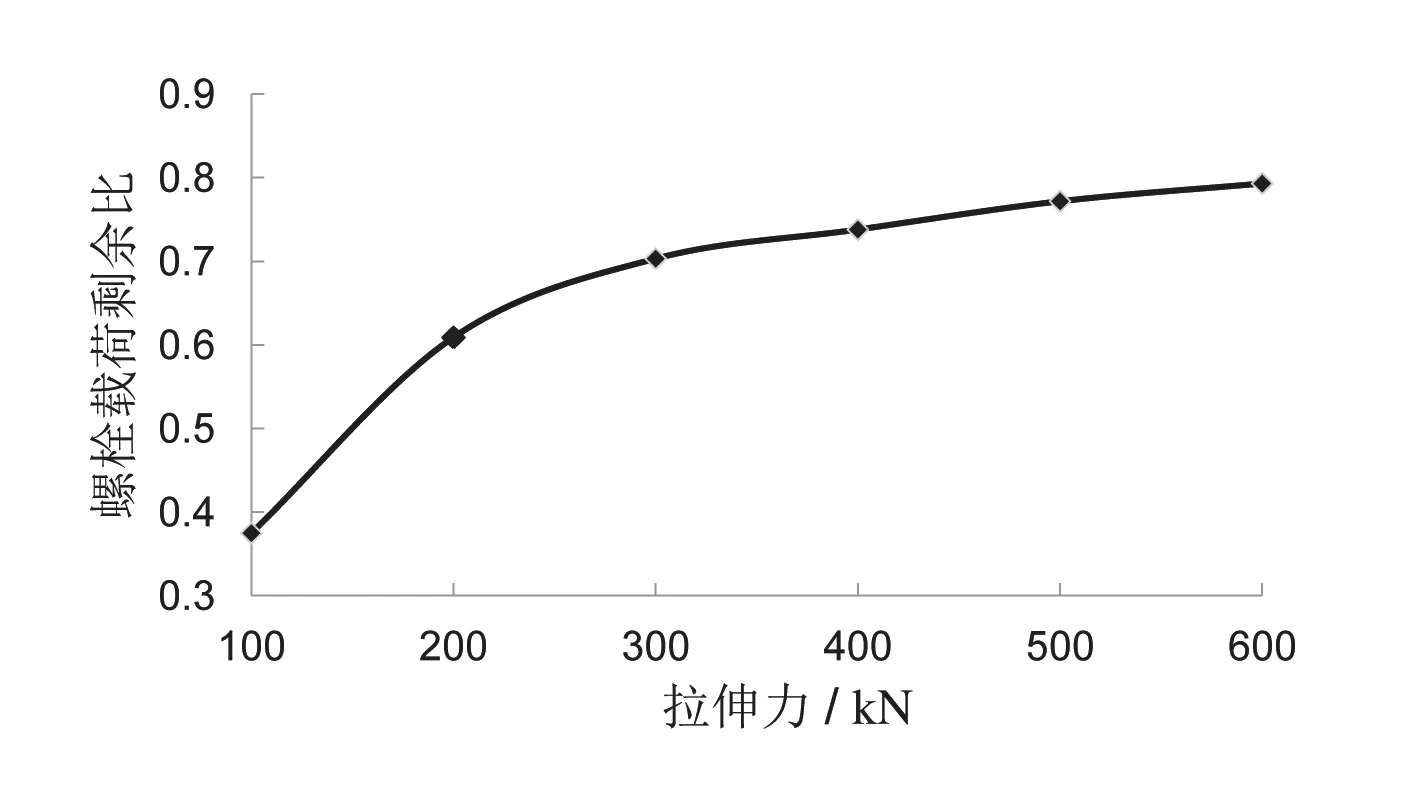
图4 拉伸力大小对载荷剩余比的影响
(二)拉伸次数对螺栓载荷剩余比的影响
对上述20组螺栓分别先后三次施加678kN的拉伸力,通过应变量测定,计算三次载荷剩余比,如表5所示。
由上述结果可知,载荷剩余比随拉伸次数增加而增大,标准差随拉伸次数增加而减小,说明螺栓拉伸-泄压后的剩余载荷在增大,且越来越稳定。而第二次拉伸和第三次拉伸结果基本相同,因此,施加螺栓目标预紧力时建议拉伸2次。
(三)时效作用对螺栓剩余载荷的影响
螺栓拉伸紧固完后,测量螺栓应变随时间的变化,如图5所示。
由图5可知,螺栓应变随时间增加而减小,最终在20h后趋于稳定。统计20组螺栓试验结果,平均应变值减小了70,对应的载荷减小1.68%。可知,螺栓载荷在螺栓紧固完成后会随时间逐步减小,并在20h后趋于稳定。
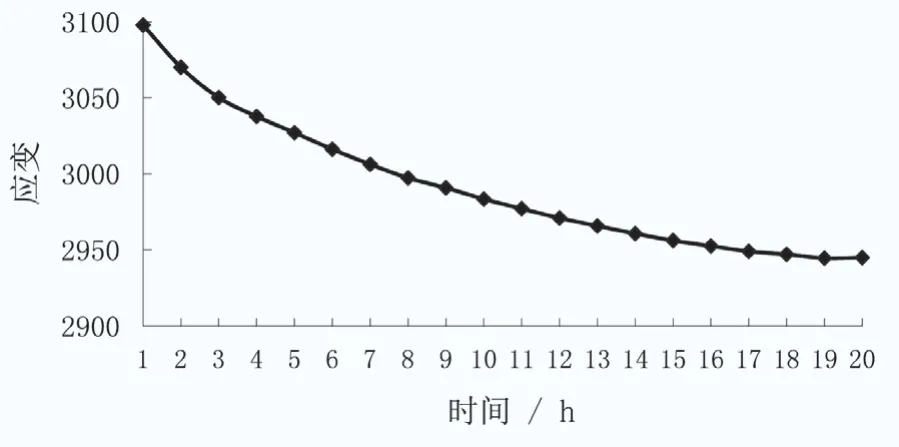
图5 螺栓应变随时间的变化
结论
本文以某大型风电机组用M36×345螺栓拉伸测试为例,通过螺栓拉伸紧固应变测试,定量分析了螺栓拉伸工艺的超拉系数、拉伸力大小、拉伸次数、时效作用等影响因素,对有效控制拉伸工艺有一定指导意义。通过试验研究发现:
(1)螺栓拉伸紧固应变测试法可行,对不同规格螺栓拉伸紧固工艺的制定具有指导意义:通过设计螺栓拉伸试验工装,可实测得到不同螺栓预紧力下的应变量,且实测结果与按VDI2230标准理论计算结果相近,试验结果可靠。
(2)根据螺栓拉伸工艺的经验公式计算所得超拉系数较应变法实测值小,存在螺栓预紧力不达标风险。通过试验研究可知,M36×345(10.9)螺栓超拉系数的经验值1.170较试验值1.281小了8.6%,综合拉伸器精度、装配精度等因素,存在预紧力超差风险。因此,制定拉伸工艺时有必要经实测得出超拉系数。
(3)螺栓拉伸-卸压后剩余载荷受拉伸大小、次数、时效作用影响,需要根据实测分析进行确认:螺栓载荷剩余比随拉伸力和拉伸次数的增加而增大,并趋于稳定;剩余载荷量随时间增加而减小,并在20h后趋于稳定。

摄影:孙佳

