半导体热敏电阻温度曲线的Matlab曲线拟合

董庆瑞

摘要：为了便于快速地找到适用的曲线拟合方法，以半导体热敏电阻实验中温度曲线的曲线拟合为例，全面地总结了利用Matlab程序进行曲线拟合的基本理论和具体方法，演示了lsqcurvefit、nlinfit和fit三个非线性拟合指令的具体程序格式与操作步骤。这些Matlab指令程序可以有效地应对实验数据处理中各种复杂的曲线拟合问题。

关键词：曲线拟合;Matlab;非线性拟合;最小二乘法

中图分类号：G642.0     文献标志码：A     文章编号：1674-9324（2019）37-0066-03

在实验数据处理过程中，经常需要选择曲线类型来拟合原始数据，并以所得曲线方程来反映变量间的函数关系[1]。随着计算机性能的提高和数值计算方法的发展，计算机软件在实验数据曲线拟合工作中发挥了越来越大的作用。目前利用计算机数值计算进行曲线拟合是实验数据曲线拟合工作的必然选择。虽然计算机语言或曲线拟合软件在实验数据的曲线拟合过程中得到了广泛运用，但对其具体操作知识的系统总结却不全面。本文以半导体热敏电阻实验中实验数据的曲线拟合为例，总结了各种Matlab拟合指令的具体用法。

一、半导体热敏电阻实验

半导体材料具有显著的热电特性，半导体热敏电阻的温度系数为负值，近似满足下式：

二、曲线拟合的理论方法

函数近似通常采用两种方法：插值法和拟合法。插值方法要求所求得的近似函数通过所有数据点，由于实验所给出的数据本身存在误差，因此要求插值曲线通过所有的插值点必定会使插值函数保留这个误差。拟合方法并不要求拟合曲线必须通过所有的数据点，只要求拟合的近似函数能够反映实验数据的整体趋势，并使拟合数据整体的误差最小。

2.多项式拟合。曲线拟合中的多项式拟合属于线性最小二乘问题，关键步骤是求解联立线性方程组，具体数学理论推导可参看相关文献[2]。在实际物理问题中，这些方程组是无解的，但可以通过数值计算方法获得其近似解。

3.非线性拟合。因为拟合函数是非线性的，所以无法如线性最小二乘法一样用求函数极值法来得到拟合参数，而需要在最小二乘法的基础上采用复杂的优化算法来求解，常用的算法是搜索算法和迭代算法[1]。搜索算法是按一定的规则选择若干组参数值，计算它们的目标函数值并比较大小，选出使目标函数值最小的参数值。不同的参数值选择规则构成不同的搜索算法。迭代算法的原则是从参数的一個初始猜测值出发，然后产生一系列的参数点，若这个参数序列收敛到使目标函数极小的参数点，则认为参数的收敛值就是所求参数点。

4.拟合方式比较。前面部分介绍的方法可以通过计算机语言进行编程来实现。Matlab也内置了现成的相关指令，在使用中无需花费时间去编程，只需要按照规定的格式调用即可。Matlab曲线拟合工具箱和Origin也集成了进行曲线拟合的软件，将数据导入软件后，可以通过操作界面对拟合过程进行设置。

程序拟合可以实现软件拟合的全部功能，相较而言软件拟合的功能有所限制。在需要进行多次重复拟合的场合，软件拟合要求对操作界面进行多次重复操作，而程序拟合却可避免这种重复操作，从而提高效率。除了处理单纯的曲线拟合工作外，拟合程序还可以嵌入复杂的数据处理程序中去发挥作用。

三、用Matlab指令进行曲线拟合

常用的Matlab曲线拟合指令有多项式拟合指令polyfit、非线性拟合指令nlinfit、非线性拟合指令lsqcurvefit、曲线拟合指令fit。下面以半导体热敏电阻温度曲线的拟合过程为例来说明这些指令的用法。

半导体热敏电阻温度曲线是一个指数函数，属于非线性拟合问题，但可以经过数学推导化简成线性拟合问题，并利用多项式拟合指令polyfit处理。本文的目的是介绍实验数据曲线拟合的普遍方法，所以仍将其按非线性拟合问题来处理，下面具体给出lsqcurvefit、nlinfit和fit三个指令的拟合过程。

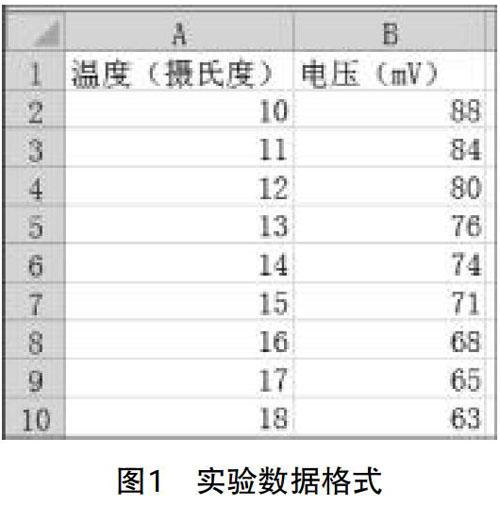
1.外部数据的输入。首先需要读取实验仪器生成的Excel数据文件并保存到Matlab的变量中，具体程序如下：

t=xlsread（'data.xls'，1，'A2：A62'）;

V=xlsread（'data.xls'，1，'B2：B62'）;

T=t+273.16;  %调整温度单位。

R=V*e-3/（20*e-6）;   %由电压计算电阻。

2.指令lsqcurvefit拟合。指令lsqcurvefit属于Matlab的优化工具箱，利用最小二乘法，从初始猜测值开始求参数，将原始数据点拟合到非线性函数，具体格式为：x=lsqcurvefit（fun，x0，xdata，ydata），其中：xdata、ydata是原始数据点;fun（x，xdata）是拟合函数，也就是公式（1）;x是拟合函数系数;x0是系数初始猜测值，其初始设置可能会影响结果。如拟合结果不理想，可以改变初始值x0后再重新拟合。具体Matlab程序如下：

x0=[2600，1000];

fun=@（x，T）x（1）*exp（x（2）*（1./T-1/300））;

x=lsqcurvefit（fun，x0，T，R）;

R0=x（1）;B=x（2）;

disp（['R='，num2str（R0），'*exp（'，num2str（B），…

'*（1./T-1/T0））']）;

计算结果如下：

R=2230.4327*exp（3407.2165*（1/T-1/T0））

拟合曲线和原始数据的对比如图2所示，结果显示拟合曲线与原始数据完全一致。如果对拟合效果要求较高，可以通过Matlab帮助系统，查阅表征拟合效果的具体参数。

3.指令nlinfit拟合。指令nlinfit属于Matlab的统计和机器学习工具箱，采用迭代最小二乘法估算拟合系数。函数nlinfit是非线性拟合的通用函数，适用面比函数lsqcurvefit更广，例如可以做加权最小二乘拟合。具体格式如下：

x=nlinfit（xdata，ydata，fun，x0）

与指令lsqcurvefit类似，不同的x0可能会得到不同的结果。具体Matlab程序如下：

x0=[2000，100];

fun=@（x，T）x（1）*exp（x（2）*（1./T-1/300））;

x=nlinfit（T，R，fun，x0）;

R0=x（1）;B=x（2）;

disp（['R='，num2str（R0），'*exp（'，num2str（B），…

'*（1/T-1/T0））']）;

计算结果如下：

R=2230.4327*exp（3407.2165*（1/T-1/T0））

这与指令lsqcurvefit的拟合结果完全一致。初始值x0设为[2000，100]，初始值的改变没有影响拟合结果。

4.指令fit拟合。指令fit屬于Matlab的曲线拟合工具箱，其功能与曲线拟合工具箱软件cftool类似。具体格式如下：

fitobject=fit（xdata，ydata，afitType）

aFittype=fittype（expression，Name，Value）

其中参数具体含义可查看Matlab帮助系统。与指令lsqcurvefit和nlinfit不同，指令fit不必设置拟合系数初始值。具体Matlab程序如下：

X=fittype（'R0*exp（B*（1/T-1/300））'，…

'independent'，'T'，'coefficients'，{'R0'，'B'}）;

Y=fit（T，R，X）;

disp（['R='，num2str（Y.R0），…

'*exp（'，num2str（Y.B），'*（1/T-1/T0））']）;

计算结果如下：

R=2230.4328*exp（3407.2159*（1/T-1/T0））

拟合结果与前面两个指令的拟合结果几乎一致。

四、结论

采用计算机数值计算方法，可以进行高精度、高效率的实验数据曲线拟合工作。本文以半导体热敏电阻实验的曲线拟合过程为例，全面总结了利用Matlab程序进行数据曲线拟合的基本理论和具体方法。具体介绍三个Matlab指令的使用方法和程序格式。应用Matlab程序进行曲线拟合，不但可以将数据拟合成各种函数，而且便于将其代码集成到复杂的实验数据处理程序中去，从而有助于完成高效、精确的实验数据处理工作。

参考文献：

[1]刘金远，段萍，鄂鹏.计算物理学[M].科学出版社，2012.

[2]彭芳麟.计算物理基础[M].北京：高等教育出版社，2010.

Curve Fitting of Temperature Curve of Semiconductor Thermistor Based on Matlab

DONG Qing-rui

（School of Physics and Electronics，Shandong Normal University，Ji'nan，Shandong 250014，China）

Abstract：To find an appropriate curve-fitting method quickly，taking the curve fitting of the temperature curve of a semiconductor thermistor as an example，the basic theory and method of curve fitting using Matlab programs are summarized comprehensively.The program format and operation steps of three non-linear fitting instructions，lsqcurvefit，nlinfit and fit，are demonstrated.These MATLAB instruction programs can effectively deal with various complex curve fitting problems in experimental data processing.

Key words：curve fitting;Matlab;nonlinear fitting;least-square method