圆孔蜂窝梁挠度计算孔型等效模式探讨

曾欢艳 张娟文 刘文祥 陈婉若

【摘 要】圆孔蜂窝梁挠度计算有实用估算法、比拟法和有限元法。论文基于费氏空腹桁架法，探讨圆孔蜂窝梁挠度计算时孔型等效的三种模式，与廖曙波等的积分计算进行对比，得出等效法一是最接近实际的孔型等效模式，从而简化计算公式，将其用于工程计算。

【Abstract】There are practical estimation method， analogy method and finite element method in calculating deflection of circular hole castellated beams. This paper discusses three modes of pass equivalence in deflection calculation of circular hole castellated beams based on Altfillisch's vierendeel truss method. By comparing with the integral calculation of Liao Shubo et al.， it is concluded that the first equivalent method is the closest one to the actual pass mode， thus we can simplify the calculation formula and apply it to engineering calculation.

【关键词】圆孔蜂窝梁;挠度;费氏空腹桁架法;孔型等效

【Keywords】 circular hole castellated beams; deflection; Altfillisch's vierendeel truss method; pass equivalence

【中图分类号】TU391                                          【文献标志码】A                                【文章编号】1673-1069（2019）08-0180-03

1 引言

圆孔蜂窝梁是一种腹板成排开圆孔的新型钢梁，其截面形式通常为工字型或槽型。圆孔蜂窝梁孔型光滑，受力合理，在工程中得到了广泛应用。

蜂窝梁的挠度是工程设计的一个控制指标。现阶段蜂窝梁的挠度计算方法大致可分为三类，即实用估算法、比拟法和有限元法[3-4]。

廖曙波等凭借自己扎实的数学功底，利用比拟法中费氏空腹桁架法原理，推导了圆孔蜂窝梁的挠度计算公式。由于没有考虑孔型等效，该公式为积分表达式，需要借助数学计算工具如MATLAB才能计算[1]。本文在此基础上，探讨圆孔蜂窝梁挠度计算时的孔型等效模式，尽量将计算公式简化，能用于工程计算。

基于廖曙波等的思路，本文共探讨三种等效模式：面积相等、惯性矩接近的正方形（简称等效法一）;面积相等、孔长不变的长方形（简称等效法二）;孔高孔长均不变的正方形（简称等效法三）。利用费氏空腹桁架法的原理，推导出考虑孔型等效后的挠度计算公式，再与廖曙波等的结果进行对比，分析出最接近实际孔型的等效模式。

2 等效法一撓度计算表达式推导

Altfillisch将蜂窝梁的挠度分解成三部分：f=fm+fv+fvm 。式中，fm是弯曲挠度，fv是剪切挠度，fvm是剪力次弯矩产生的梁桥及墩腰转动而引起的挠度[2]。

2.1 弯曲挠度

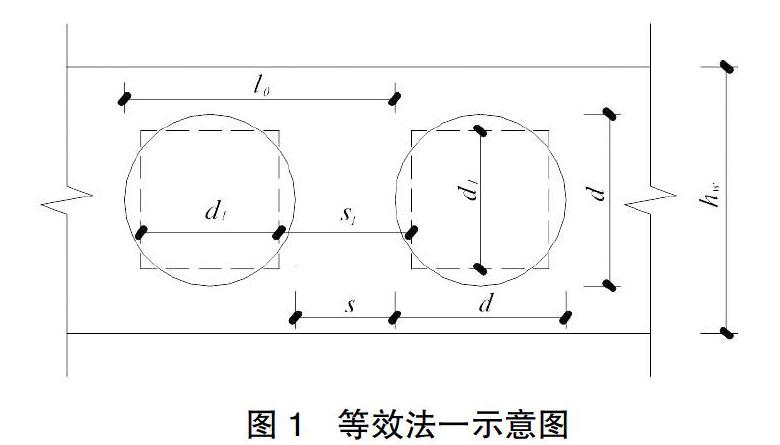
等效模式如图1所示，蜂窝梁圆形孔直径d，开孔间距s。按面积相等，惯性矩最接近的等效原则，将圆形孔等效为正方形孔，等效尺寸为d1和s1。

定义蜂窝梁正方形开孔空腹部分的等效截面惯性矩为Ik1;实腹部分的截面惯性矩为IS;换算实腹梁（与蜂窝梁实腹部分尺寸相同的实腹梁）的惯性矩也为IS;蜂窝梁的一个孔长加一个间距长为一个单元，其长度l0=d+s。求得等效正方形的边长d1及s1：

蜂窝梁正方形开孔部分的等效惯性矩为：

现设有一简支圆形孔蜂窝梁，如图2所示，圆形孔直径为d，开孔间距s，端距为s/2。梁两端作用有纯弯矩M，设其总长为L。

将圆形孔洞全等效为正方形孔如图所示，可知梁的抗弯刚度沿梁长是变化的。假设梁长共有n个单元，第i个开孔边缘距梁端的距离：

3  等效法二挠度计算表达式推导

考虑到开孔长度对蜂窝梁挠度的影响，可将圆形孔等效为面积相等、孔长不变的长方形。此时孔长为d，孔高a==πd=0.785d，开孔部分惯性矩Ik2=Is-twa3，腹板面积Ak2=As-atw，空腹部分占全长比例为=。同等效法一推导过程，可知：fm=f（s+d）;fv=f（s+d） （10）

剪力次弯矩产生的挠度fvm同等效法一，参数相应的进行改变即可。

4  等效法三挠度计算表达式推导

考虑到孔高和孔长两者同时对蜂窝梁挠度的影响，可将圆形孔等效为孔高孔长均不变的正方形。此时孔长=孔高=d，开孔部分惯性矩Ik3=Is-twd3，腹板面积，同理可知：

剪力次弯矩产生的挠度fvm仍同等效法一，参数相应的进行改变即可。

5 不同等效模式的比较分析

以某简支圆形孔蜂窝梁为例，梁截面尺寸H450×200×8×10，蜂窝梁跨度L=8100mm，材质Q235B。梁上翼缘作用均布荷载q=25kN/m。现以蜂窝梁的孔高比d/hw和距高比s/hw为变量，分别用三种等效方法计算蜂窝梁挠度，并与廖曙波等的计算结果进行对比分析，结果如表1所示。

将上表数值用变化关系图表示如图4所示。

从表1及图4得出以下规律：

①圆孔蜂窝梁挠度随着孔高比d/hw的增大而增大，随着距高比s/hw的增大而减小。

②等效法三由于扩大了孔洞面积，削弱了截面，导致挠度比实际情况大，特别当孔高比d/hw=0.8，距高比s/hw=0.4时，等效法三挠度达到了廖曙波等计算结果的1.3倍以上，相差较大，等效模式不可取。

③等效法一和等效法二，计算结果与廖曙波等的计算结果接近，可见开孔面积对挠度的影响占主要作用[3]。其中，等效法一（即等效为面积相等、惯性矩接近的正方形）计算结果偏于安全，故本文推荐圆孔蜂窝梁的孔型等效模式为等效法一。

跨中集中荷载作用下圖形变化规律与均布荷载作用情况类似，限于篇幅，本文不再赘述。

6 结论

①本文基于费氏空腹桁架法原理，推导了圆孔蜂窝梁孔型三种等效模式下的挠度计算公式，并将计算结果与廖曙波等的积分计算进行对比，得出等效法一（即等效为面积相等、惯性矩接近的正方形）是最接近实际状态的孔型等效模式[4]。

②根据等效法一的计算结果，本文推荐圆孔蜂窝梁挠度计算时可采用式（6）（7）（8）和（9）进行理论计算。与廖曙波等的积分计算相比，该计算公式大大简化了工作量，并能达到一定的计算精度要求。

【参考文献】

【1】廖曙波，罗烈.基于费式空间桁架法的简支圆孔蜂窝梁挠度计算[J].建筑结构，2017，47（S1）：812-818.

【2】曾欢艳.考虑孔高比和距高比正六边形孔蜂窝梁挠度计算研究[D].长沙：湖南大学，2013.

【3】冯春燕，于大永.蜂窝梁挠度计算方法研究[J].四川建筑科学研究，2012（1）：65-69.

【4】王亚云，闫宁霞，等.工字形截面圆孔蜂窝梁的挠度分析[J]. 工程设计，钢结构，2018（11）：97-101.