基于随机车流的桥梁构件疲劳分析及其疲劳荷载模型研究

李绍华

摘  要：精细化的结构性能评估是桥梁大建设后的前沿性课题，可为桥梁的运营、管理和维护提供持续性优化。目前，诸多桥梁在运营使用多年后出现了大量的病害及損伤，对于桥梁构件疲劳性分析研究意义重大。芜湖长江公路二桥构建系统在活载作用下的疲劳性能非常突出，模拟正常随机车流作用下的构件疲劳应力幅特性，建立疲劳车辆荷载模型。

关键词：随机车流作用;正交异性桥面板;构造细节;疲劳性

中图分类号：U441.4        文献标志码：A 文章编号：2095-2945（2019）27-0049-03

Abstract： Refined structure evaluation has become one of the most popular research topics nowadays; the result of the researches could provide valuable continuous optimization for the operation， management and maintenance of the bridge. At present， a lot of issues and damages start to occur after the bridges being in use for several years; therefore， it is important and meaningful to study the fatigue of bridge members further more. The fatigue characteristic of Wuhu Yangtze River Highway Second Bridge under live load is prominent. This research simulates the fatigue stress amplitude under random traffic flow state based on Wuhu Yangtze River Highway Second Bridge， and establishes the fatigue vehicle load model according to the research results.

Keywords： random traffic flow affection; orthotropic bridge deck; structure detail; fatigue

引言

提高运营期桥梁受荷效应的评估精度，对于降低运营期间发生的显著损伤及垮塌等恶性事故、优化全寿命成本，具有重大意义。Jacob等使用WIM技术，实测车辆信息、车辆实距、交通流量和车辆跟驰等车流信息[1]。Lee等通过图像处理技术识别车辆位置及复杂变道、跟驰等微观交通信息[2]。Hollander研究了车辆加速、减速、换道等微观驾驶行为对桥梁荷载的影响[3]。Chen等应用了交通领域的元胞自动机建模技术，引入随机性交通元胞自动机，进行荷载流仿真[4]。Xia等指出对于正交异性桥面板问题，由于其显著影响区域非常有限，可以模拟车轴的作用计算其疲劳性能[5]。Nowak指出对于简支梁桥跨中弯矩的疲特性需将详细车辆信息等特性考虑进去[6]。芜湖长江公路二桥采用四面索同向回转拉索体系及正交异性钢桥面板，这两个构件在活载作用下的构建疲劳性能较突出，本文通过模拟正常随机车流作用下的构件疲劳应力幅特性，研究等效于实际车流作用状况的疲劳车辆荷载模型。

1 拉索疲劳荷载效应及疲劳车辆荷载模型

1.1 随机车流模拟工况

影响疲劳累积损伤的因素很多，如：平均应力、少数极高应力、应力次序、低疲应力，重复循环块的大小以及材料本身都对累积损伤有较大的影响。将变幅疲劳转化为常幅疲劳的方法如下。构造细部的常幅度疲劳曲线方程为：

（1）

由此可得该构造细部在Δσi、ni（i=1，2，3......）重复荷载作用下的损伤度为：

由上式可得该构造细部在“等效常幅Δσ0”应力循环作用下的疲劳破坏次数为N0：

以Δσ0重复∑niN0次时的损伤度为：

令Db=D0，则有：

于是有：

（6）

针对斜拉索的疲劳车辆荷载效应计算，模拟正常车留下拉索的应力情况，并根据雨流计数法计算拉索的应力幅频次曲线，最后基于线性损伤准则获得斜拉索的等效疲劳应力幅。本文考虑不同日均交通流量的作用，计算中跨跨中拉索、中跨四分点拉索和中跨近塔柱处拉索的应力幅和月累计频次。

1.2 疲劳荷载效应分析

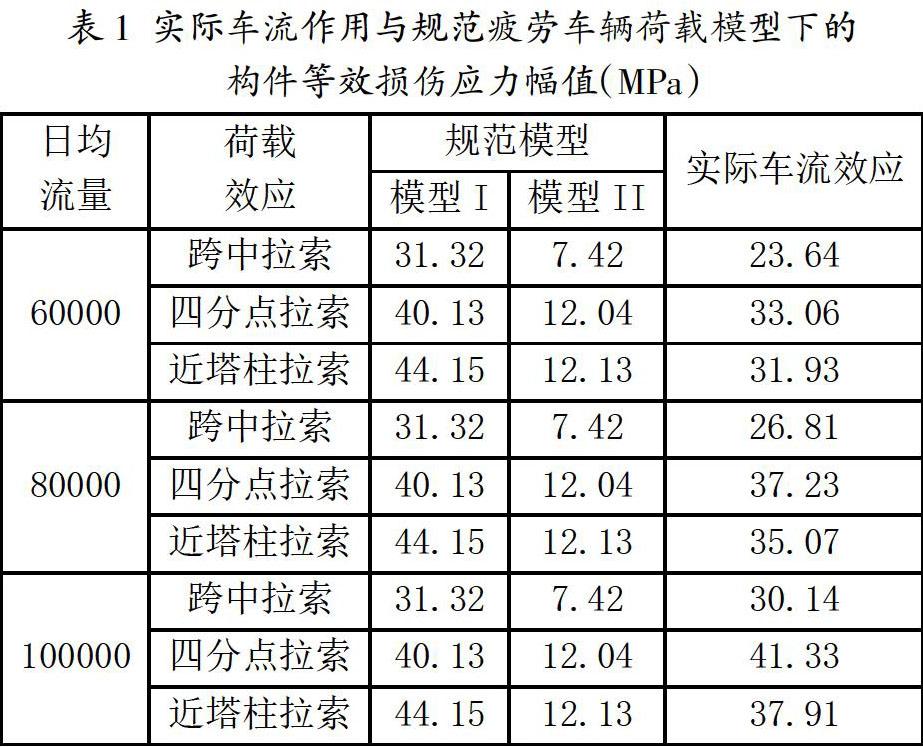
基于线性损伤累积准则和雨流计数法，可以计算不同交通流量下的各关键拉索的等效应力幅和月累计频次，如表1所示。随着日均交通流量的增加，拉索等效应力幅近似呈现线性变化，可用函数表示：

（7）

Δσ-拉索等效应力幅;

Δσq-交通流量。

三个典型的拉索构件中，中跨跨中拉索的等效应力幅是最低的，中跨近索塔处拉索的等效应力幅是最高的，说明短拉索的应力幅更大，其疲劳效应问题也更加突出。

1.3 与规范疲劳模型的比较

表1对比了实际车流作用与规范疲劳车辆荷载模型下的拉索等效损伤应力幅。可见，模型I计算的等效应力幅显著大于模型II的结果，模型I更为不利。通过对比模型I与实际车流效应下的等效应力幅，可以看到实际车流作用下的等效应力幅基本上低于规范疲劳模型I，由于疲劳荷载模型I定义的是有限寿命设计状态，采用规范疲劳模型I进行计算能够保证拉索的疲劳安全性。

1.4 疲劳车辆荷载模型

考虑到大跨径斜拉桥拉索影响面的分布特点，可以沿用目前《公路钢结构桥梁设计规范》（JTG D64-2015）所規定的疲劳荷载模型的形式，所采用的均布荷载大小根据实际车流作用下的等效应力幅反算其取值。最终推定拉索疲劳车辆荷载效应评估模型为qk=4kN/m，Pk=560kN，η=0.05AADT+0.6，qk，Pk均为三车道取值。

（8）

η-交通流量对均布荷载集度的修正;

qk-交通流量80000veh/d均布线荷载集度取值;

Pk-交通流量80000veh/d集中荷载取值。

2 正交异性桥面板疲劳荷载效应与模型

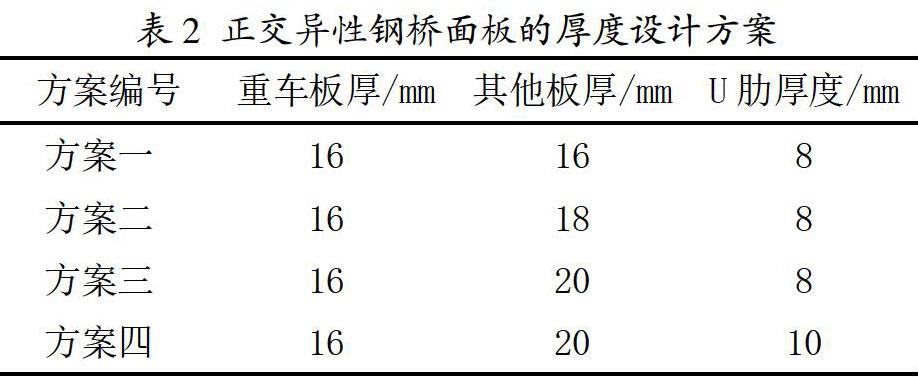
芜湖二桥采用正交异性钢桥面板，其结构疲劳问题尤为突出。采用对板厚、肋厚的参数化分析，选取合理方案。

2.1 疲劳分析方法与车辆荷载模拟

2.1.1 分析方法

热点应力法考虑了结构应力集中效应，弥补完善了名义应力法。焊趾自身缺口效应则在S-N曲线中考虑。焊接结构中的热点是焊趾处一临界位置，结构热点应力计算方法是基于对该位置进行力学性能评估。由于焊接构件存在焊缝形状、切口等因素引起非线性应力峰值影响，表面外推法采用距离焊趾一定距离的参考点的表面应力，计算结构热点应力。

“a”型和“c”型焊趾处结构热点应力分布于结构厚度具有相关性，其外推点位置根据厚度确定。超出焊缝焊趾0.4倍厚度处，非线性应力峰值基本消失，应力分不出呈线性变化。“b”型焊趾处结构应力分布不依赖于构件厚度，其外推点位置以绝对数值进行确定。

2.1.2 S-N曲线的选取

众多学者经过大量综合分析及试验对比，认为当使用其建议的有限元模型及外推法确定热点应力值时，可以应用FAT90作为一条通用的热点应力S-N曲线（适用于板厚t<25mm，否则应进行必要的板厚修正）。该曲线在DNV规范中得到应用，其相关参数见表3。

2.1.3 车辆荷载模拟

建立钢箱梁节段有限元模型，通过热点应力法获取构造细节应力状态。采用随机车流模拟，仅需考虑纵向单个重车的轮载对桥面板作用，考虑所有车辆的横向位置方差900mm2，所有车道均相同考虑，按照0.3m的横向间隔对车轮横向位置的概率统计，发现呈正态分布状态。

模拟持续30天，通过影响面加载，获得给定细节的应力时程结果，通过雨流法计数获得应力幅频次曲线，并参照AASHTO规范的疲劳分析考虑1.05的冲击系数。

2.2 构造细节疲劳荷载效应分析

通过分析不同桥面板厚度组合下的结构细节应力时程结果，计算其等效损伤应力幅值。结果表明，随机车流作用下的疲劳细节等效应力幅比规范稍大;重车道钢板厚度的增加，会减少结构细节的疲劳应力幅值;U型加劲肋厚度的增加，可以有效降低构造细节疲劳应力幅50%以上。综上所述，对于芜湖二桥正交异性桥面板的疲劳设计推荐使用方案：重车道18mm+轻车道16mm+U型加劲肋8mm的组合模式。

3 疲劳车辆荷载模型推导

正交异性桥面板的构造细节影响面的分布范围是有限的，控制正交异性钢桥面板构造细节疲劳荷载效应的主要是车辆的车轮加载。考虑超载重车作用，拟对现有的疲劳车辆荷载模型进行修订。基于上述研究结论，推导的疲劳车辆荷载模型基本沿用目前《公路钢结构桥梁设计规范》（JTG D64-2015）的疲劳计算模型，轴重取值70kN+140kN+140kN的组合方式。

4 结束语

文章研究了随机车流作用下桥梁构造的疲劳特性并推定了用于构件疲劳分析的车辆荷载模型。根据芜湖二桥的设计特点，提出了基于实际车流作用特点的桥梁构件疲劳评估用车辆荷载模型。

参考文献：

[1]Ieng S S. Bridges Influence Line Estimation for Bridge Weigh-in-Motion System[J]. Journal of Computing in Civil Engineering， 2014，29.

[2]Lee J J， Shinozuka M. Real-Time Displacement Measurement of a Flexible Bridge Using Digital Image Processing Techniques[J]. Experimental Mechanics， 2006，46（1）：105-114.

[3]Hollander Y， Liu R. The principles of calibrating traffic microsimulation models[J]. Transportation， 2008，35（3）：347-362.

[4]Wang Y P， Zhou Y H， Wu P， et al. Simulation of Railway Network Based on Cellular Automaton Model with Conflict Resolution[J]. Applied Mechanics and Materials， 2011，48-49：1069-1072.

[5]Zhu H B， Xia B， Zhao Y. RC Beam Bridge's Fatigue Cumulative Damage Rule Research[J]. Advanced Materials Research， 2013，787：4.

[6]CHEUNG， M. S， LI， etal. Probabilistic fatigue and fracture analyses of steel bridges[J]. Structural Safety， 2003，25（3）：245-262.