基于格兰杰因果的神经元功能连接分析
汪跃萍 朱云国
(铜陵学院,安徽 铜陵 244061)
一、引言
多通道神经信号记录技术的发展,了解多神经元如何协同工作以及神经元的连接关系,能为获得某种特定脑功能活动提供帮助[1,2]。在伸展抓握过程,神经元在不同的动作时段都伴随中神经元放电,分析在动作谋划时段和动作执行时段神经元放电活动的差异性,为我们接下来分析神经元的连接关系打下基础。本文通过基于copula(连接)函数的Granger Causality(格兰杰因果关系)去生成格兰杰因果网络[3],引入网络复杂性去分析神经元在动作执行时段与动作谋划时段的连接水平。
二、方法
(一)格兰杰因果网络的构建
1.连接函数
Copula函数是将多变量联合累积分布函数与各变量边缘累积分布函数连接起来的函数[4,5]。若Y是多变量的联合分布函数,Yi是各变量的边缘累积分布函数,C为多变量的连接函数,则Y(x1,x2,…,xn)=C(Y1(x1),Y2(x2),…Yn(xn))。
推论1设x与y的联合分布函数是H(x,y),它们的各变量的边缘分布函数分别是 F(x)和 G(y),C为相应的连接函数,F-1(u)、G-1(v)分别为 F(x)、G(y)的反函数,那么对于连接函数C定义域内的任意u,v均有:
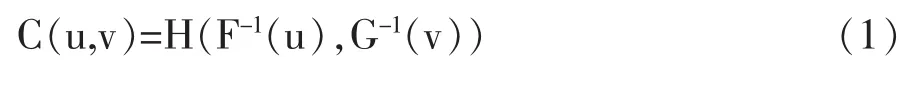
通过 C(u,v)的密度函数 c(u,v)和边缘分布函数 F(x)、G(y)可以求出分布函数 H(x,y)的概率密度函数:
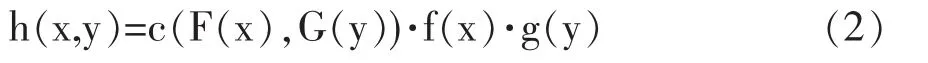
2.格兰杰因果关系
已知变量X及变量Y的历史所有信息,来预测当前时刻的变量X的概率分布要比不包含变量Y的历史所有信息来预测当前时刻的变量X的概率分布预测效果要好,能够表明Y对于X的将来变化的预测有帮助,则表明Y是X的格兰杰原因。f(Xp|Xh,Yh)表示的就是在已知X以及Y的历史所有信息这样的条件下对X的预测效果,f(Xp|Xh)表示的就是不包含Y的历史所有信息对X进行的预测效果[6]。其中X,Y是两个随机变量,f是条件概率函数。
根据格兰杰因果定义,得到格兰杰因果关系式[7,8]:
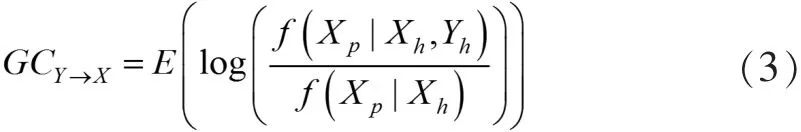
公式3中的E表示该样本空间的期望值。公式3是在未知模型的情况下直接进行概率估计,可以分析神经元与神经元非线性关系以及高阶的因果关系。
3.基于连接函数的格兰杰因果

图1 同时记录的神经元放电序列
如图1所示,同时记录的两个神经元X,Y放电信息,定义Y神经元作为触发神经元,神经元X为目标神经元,分析Y是否为X的格兰杰因果原因,X是否为Y的格兰杰因果的结果。由图1知,神经元X有N 次放电时刻,放电时刻记录为{TX,1,TX,2,…,TX,N},神经元Y有M次的放电时刻,放电时刻为{TY,1,TY,2,…,TY,M}。
TXX表示神经元X两次放电间隔时间,{TX,2-TX,1,TX,3-TX,2,…TX,N-TX,N-1},TYX表示神经元 Y 与神经元 X 两次相邻放电间隔时间,图1中由于TX,N-1与TX,N-2有相同触发神经元 TY,M-1,TYX为{TX,2-TY,1,…,TX,N-2-TY,M-1,TX,N-1-TY,M-1,TX,N-TX,M}。
用f(TXX)表示TXX的概率分布函数,表示不包含神经元Y的历史所有信息来预测当前时刻的神经元X的概率分布。f(TXX)表示的是可预测性,所以可以将 f(TXX)来表示 f(Xp|Xh)。 就将式(3)转换成式(4)。
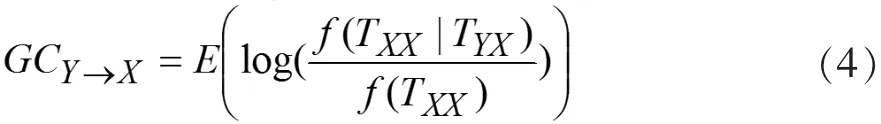
由连接函数的定义可知:
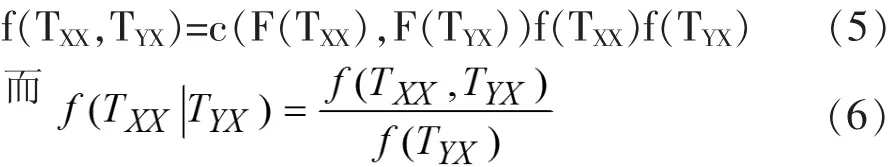
得到基于连接函数的格兰杰因果式:
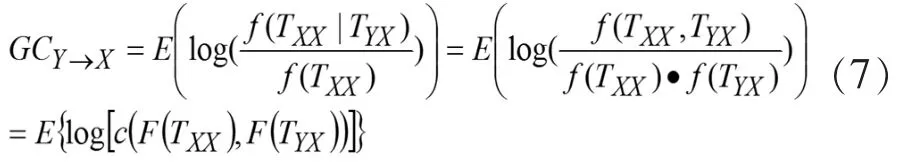
(二)网络结构复杂性
伸展抓握动作过程,分析动作谋划时段与动作执行时段的神经元格杰因果网络的复杂性,引入式(8)计算网络结构复杂性比例。

式(8)中分子GC表示伸展抓握过程动作执行时段格兰杰因果连接矩阵,分母gc表示伸展抓握过程动作谋划时段格兰杰因果连接矩阵。
三、实验结果
在伸展抓握过程,主要分析动作谋划时段以及动作执行时段。由于在动作谋划时段放电神经元数目比较少,考虑到在动作谋划时段和动作执行时段进行对比,选取7个放电比较多的神经元来分析。选取的两组数据结果,第一组数据记录的是4,11,12,13,14,15,16这7个神经元90次试验放电结果,第二组数据来源是神经元4,9,11,12,14,15,16这7个神经元90次试验放电结果。数据记录的复杂性结果如表1、表2所示。

表1 第一组90次试验网络结构复杂性分布
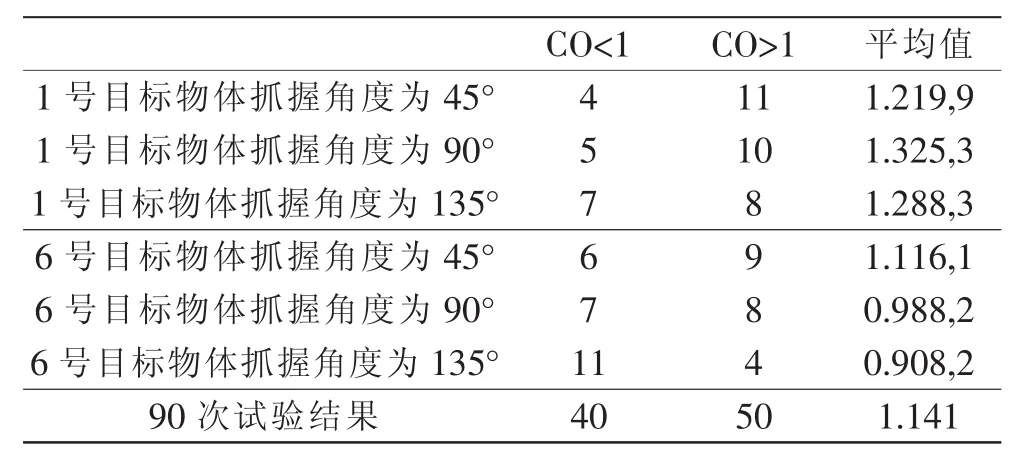
表2 第二组90次试验网络结构复杂性分布
由表1、表2知,1号目标物体抓握角度为 45°、90°、135°,6号目标物体抓握角度为45°网络复杂性比例都是大于1,且总的90次试验结果中网络复杂性比例也是大于1。也就表明伸展抓握过程中,神经元格兰杰因果连接在动作执行时段要比动作谋划时段连接要强。发现在动作执行时段,神经元功能连接网络要较动作谋划时段的神经元功能连接网络更为复杂,从而验证初级运动皮层主要功能就是动作执行。
四、结论
在完成伸展抓握过程,动作执行时段与动作谋划时段对比,神经元与神经元之间会出现更多的格兰杰因果连接。出现在动作执行时段,神经元连接更为复杂这一现象的原因在于:动作执行时段,猕猴的运动皮层的神经系统需要对实时的外界反馈做出反应,完成持续的输入输出的闭环动作控制,所以需要神经元之间更加频繁的交互,需要交流更复杂的信息,更复杂的协助。在动作谋划时段,主要任务是自我确认和准备对应的任务目标,也很可能是猕猴会对动作执行的时段的提前预演,但这些所处理的信息与比动作执行时段所处理的动作学信息要少得多,所以猕猴在动作谋划时段的神经元功能连接相对简单,从而验证初级运动皮层主要功能就是动作执行。

