基于Stackelberg模型下边际成本变化对技术创新的影响

马永红， 李言睿,2

(1.哈尔滨工程大学 经济管理学院，黑龙江 哈尔滨 150001; 2.哈尔滨师范大学 经济学院，黑龙江 哈尔滨 150025)

0 引言

在当前市场环境下，运作成本的降低、产品技术的创新是企业赢得生存和发展的关键因素。面对产品生命周期的缩短、市场不确定性和技术复杂性的增加这一大环境，企业需要持续大量投资进行技术创新以保持竞争优势[1]。苏屹等用实证分析等方法对我国高技术企业技术创新绩效进行了评价[2]，结果显示大量技术创新成果并不能得到有效转化。创新成果商品化后企业是否能获得利润是关键因素，因此，控制好技术创新后边际成本变化与产品价格关系，成为企业获得利润的重要因素。我们用边际成本变化率来衡量企业技术创新投入成本，可以推断，在某个数值以内创新会给企业带来利润的增加，超过该值，由于投入资金过多导致产品价格过高等原因，可能致使企业利润下滑，此时，基于利益考量，企业可能选择不创新。所以，边际成本变化对企业技术创新影响的研究就显得尤为必要。

技术创新理论由J.A.SchumPeter创立，而后又由D’Aspremont 和Jacque minde首次将博弈论引入到技术创新中，分析了双寡头垄断博弈在技术创新中的博弈行为[3]。Nicholas S.Vono-tras、Suzumura 采用三阶段博弈模型对技术创新策略进行了分析，Kotaro Suzumura 运用两阶段动态博弈模型对技术创新策略进行了分析[4]。传统Stackelberg模型是线性需求下，两企业在同质产品市场中以产量为决策变量进行的序贯博弈模型，许多文献对其假设条件进行了改进和扩展[5～11]。姚丰桥等证明了Stackelberg双寡头是否采用技术创新策略不但与技术创新前后成品的边际成本、价格相关，也与企业在市场中的地位有关，因此双方基于利益考量不一定采取一致的技术创新策略[12]。陈圻通过建立低成本创新的产品价格决策及创新投入三阶段博弈模型，系统深入地研究了水平差异双寡头厂商的产品功能问题，获得了对低成本创新有重要意义的一系列新的结论[13]。另外，许多学者从不同角度研究了技术创新决策[14～17]，以曾鸣、Williamson为代表的学者发现，一些企业擅长通过创新在新产品质量、功能和成本之间找到比较难把握的平衡[18]。马永红等从创新过程—创新产出—创新经济效益三个维度构建高技术产业创新质量评价体系, 结果表明,我国高技术产业创新质量普遍不高,且空间差异性明显[19]。王丽丽等用动态博弈方法分别对供应链上下游企业及供应链间企业的技术创新进行分析，推导出了企业利润均衡函数[20]。左晓璐等在随机需求和技术变革的环境下,基于有产能约束的单供应商—单零售商的供应链结构,研究了供应商分销价格决策和技术创新策略以及零售商订货决策[21,22]。

通过对以往文献的整理发现，已经有很多文章研究了技术创新策略的影响因素，但大部分文章将重点放在了创新成本投入对技术创新策略的影响上，而边际成本变化对技术创新策略的影响方面的研究比较少，这也给本文研究带来了一定困难。本文试图在单生产商—多零售商供应链结构下，通过建立零售商Stackable博弈模型，得到产品边际成本变化对生产商技术创新策略的影响。具体探讨以下问题：首先讨论了产品边际成本的变化对产品销量及价格的影响，其次讨论了产品销量和价格的变化对生产商利润的影响，最后生产商根据其利润的变化制定技术创新策略。

1 模型构建与分析

1.1 模型描述与假设

当一种产品原有技术优势不可避免的丧失，市场逐渐陷入同质化产品竞争时，生产商会采取利用技术创新方式来获得更多利润。技术创新必然使得边际成本有所提高，边际成本的变化又影响了产品的价格和销量，那么，选择新技术是否能给生产商带来更多利润成为了一个问题。在这里，引入参变量δ来表示技术创新后的产品边际成本的变化率。首先根据模型得到一个期望的销量，在此销量下，我们假设企业技术创新投入的成本全部体现在产品边际成本的变化率上，也就是说，将技术创新投入的所有成本都平均到单位产品成本中，不单独考虑固定成本。目的是通过边际成本的变化率δ得出一个企业技术创新成本投入的最佳方案，通过参量δ的变化，证明在某个范围内投入成本技术创新能给企业带来更高的利润，企业根据其来决定是否创新。

假设1当产品流入市场初期，假设为单供应商—单零售商的双层市场结构，上游为垄断生产商M，下游为零售商R1直接向消费者出售产品，这一时期零售商不存在竞争，生产商M根据零售商R1的销量生产产品。

假设2生产商的生产能力不受限制，经过一段时间后生产商需要技术创新以获得更高利润，且跟随者零售商R2进入该销售区域，创新后生产商M向零售商R1提供旧技术和新技术两种产品，向零售商R2提供新技术产品。

假设3旧技术产品成本为C1，技术创新后边际成本变化率为δ(由文献[12]可知，当δ<0时必然选择技术创新，因此我们讨论δ>0时的情形)，技术创新后产品成本为C2=(1+δ)C1，设技术创新后产品质量水平为S。

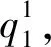
参数θ表示其他产品销量或其他零售商销量对价格的影响。

假设5为了从理论上考察边际成本变化对技术创新的影响，本文假设上下游交易为完全信息的。

生产商M，零售商R1，R2的利润函数如下：

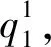
采用逆序归纳法求解整个博弈过程，如下图：

1.2 零售商的订货策略

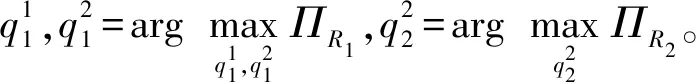
命题1旧技术产品的市场均衡销量为

对于新技术产品零售商R1的市场均衡销量为

零售商R2的市场均衡销量为

证明将反需求函数带入零售商R1，R2利润函数可得

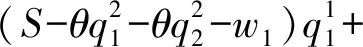
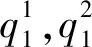
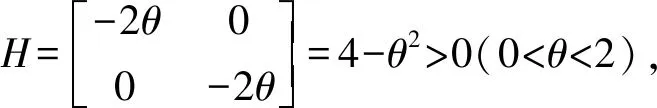
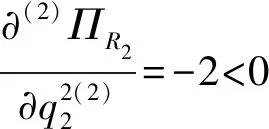
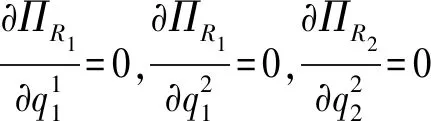
推论对于零售商R1而言，旧技术产品的销量大于新技术产品销量，对于新技术产品而言，零售商R2的销量大于零售商R1的销量。

1.3 生产商主导的批发价格决策

企业观察到市场的期望销量，也就是命题1中得到的均衡，根据其确定批发价格w2=(1+δ)w1。企业的目的是利润最大化，提高批发价格可能导致销量降低，但单个商品的利润提高了，同时，商品的质量和功能改善也会促进一些消费者购买。在这一阶段，我们暂时不考虑产品扩散速度，从企业利润最大化的角度确定批发价格。

命题2当边际成本变化率为δ时，生产商确定批发价格为

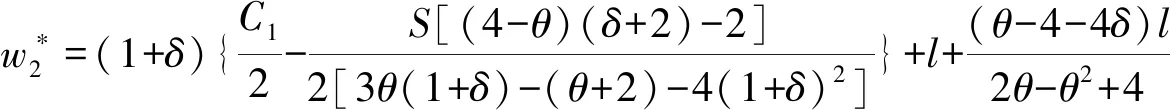
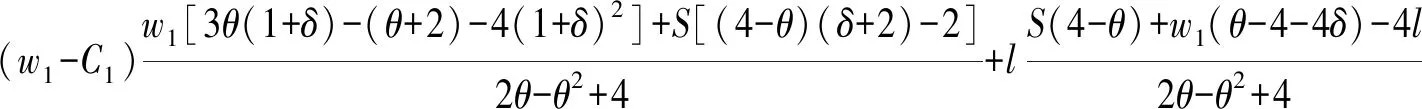
根据利润最大化原则可得：

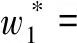
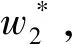
1.4 生产商的技术创新策略

企业看到市场需求，确定边际成本变化率δ的最佳取值，也就是说，这一阶段我们要得到δ是如何影响企业利润的，企业将如何根据边际成本变化率δ的来制定技术创新策略。

命题3当边际成本变化率为δ*=A时，最有利于生产商进行技术创新。

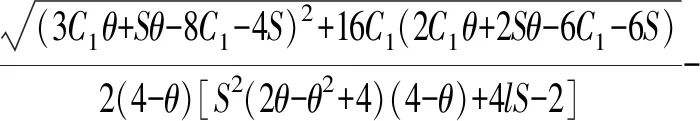
证明将w2代入生产商利润函数中可得：

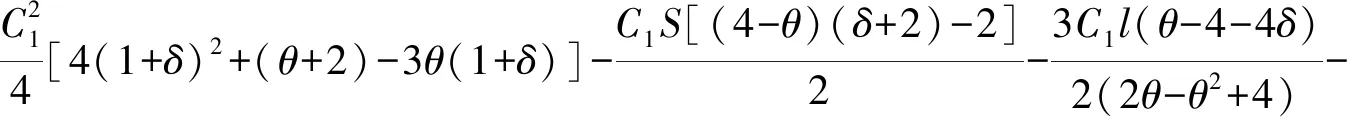
根据利润最大化原则即可得到δ*=A为生产商利润函数的极大值，也就是说，技术创新后边际成本在C2=(1+A)C1附近时，生产商可获得较多利润，那么会选择创新。实际上，A是一个极大值，当δ>A时企业利润呈下降趋势，因此，生产商更愿意将边际成本控制在C2<(1+A)C1。

2 扩展讨论

2.1 产品定价与创新

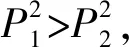
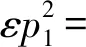
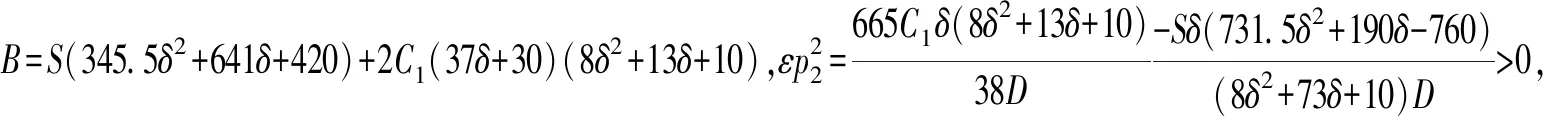
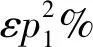
2.2 质量与创新

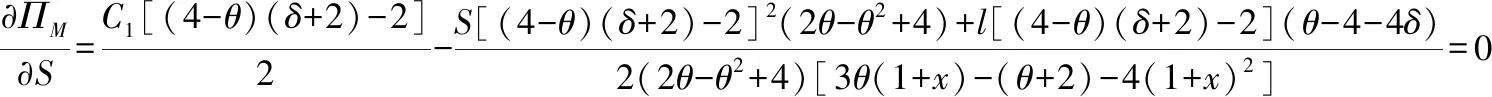
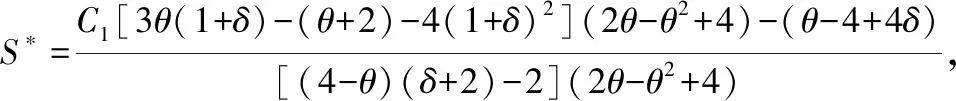
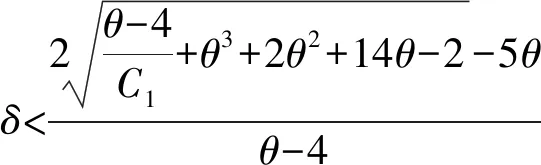
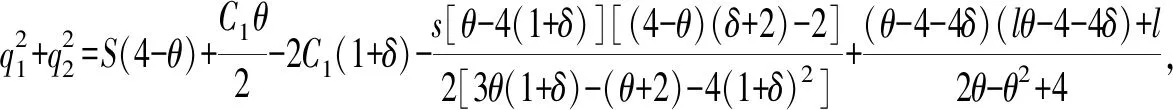
以上模型是假设当前市场确实需要技术创新，而现实的商品市场是具有不确定性的，生产商需要先观察市场是否需要技术创新。同时，我们得到的结论是从供应链整体出发的，不能保证单个零售商利润最大。

3 算例分析

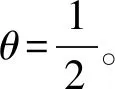
图1说明技术创新后产品批发价格随着投入成本的增加而增加，企业为了赚取利润，显然投入的成本越多，批发价格越高，这是自然规律。同时，旧技术产品批发价格随之下降。这种情况在高科技产品中是常见的，比如人们所熟悉的家电和手机，随着新产品的开发，原有技术下的产品逐渐降价。技术开发投入的越多，新技术产品功能越好，随之售价也就越高，对比之下，旧技术产品在市场上的价格也就越低，当价格降低到一定程度时，企业得不到利润，这时生产商不再生产旧技术产品。这也说明了高科技产品为什么更新换代快，因为不更新，不利用新技术，产品就会被淘汰，企业就得不到更多利润。

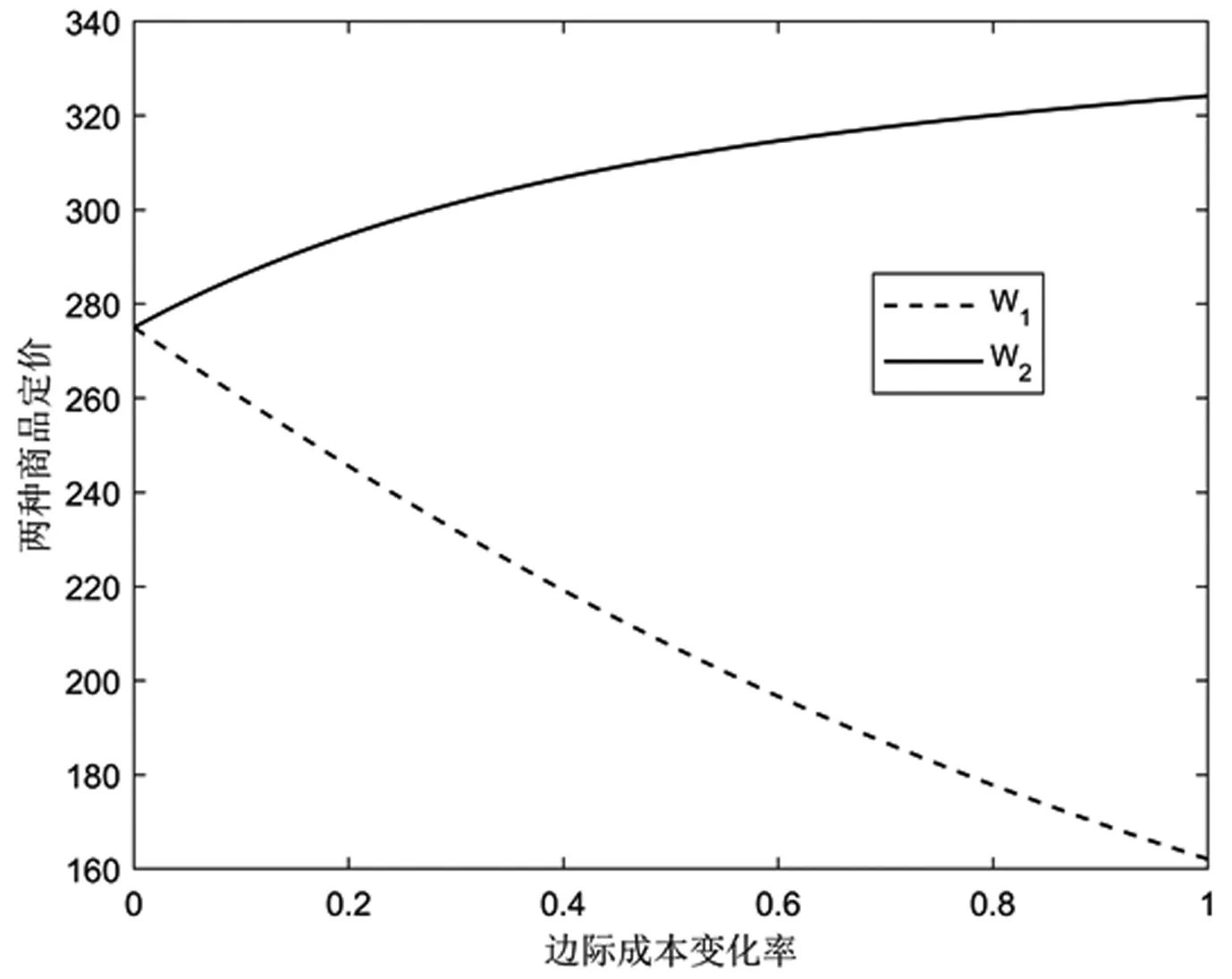
图1 批发价格变化图

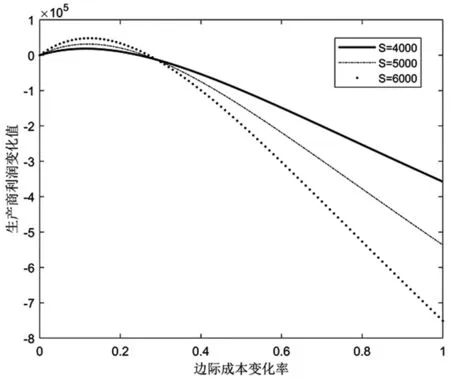
图2 生产商利润变化图

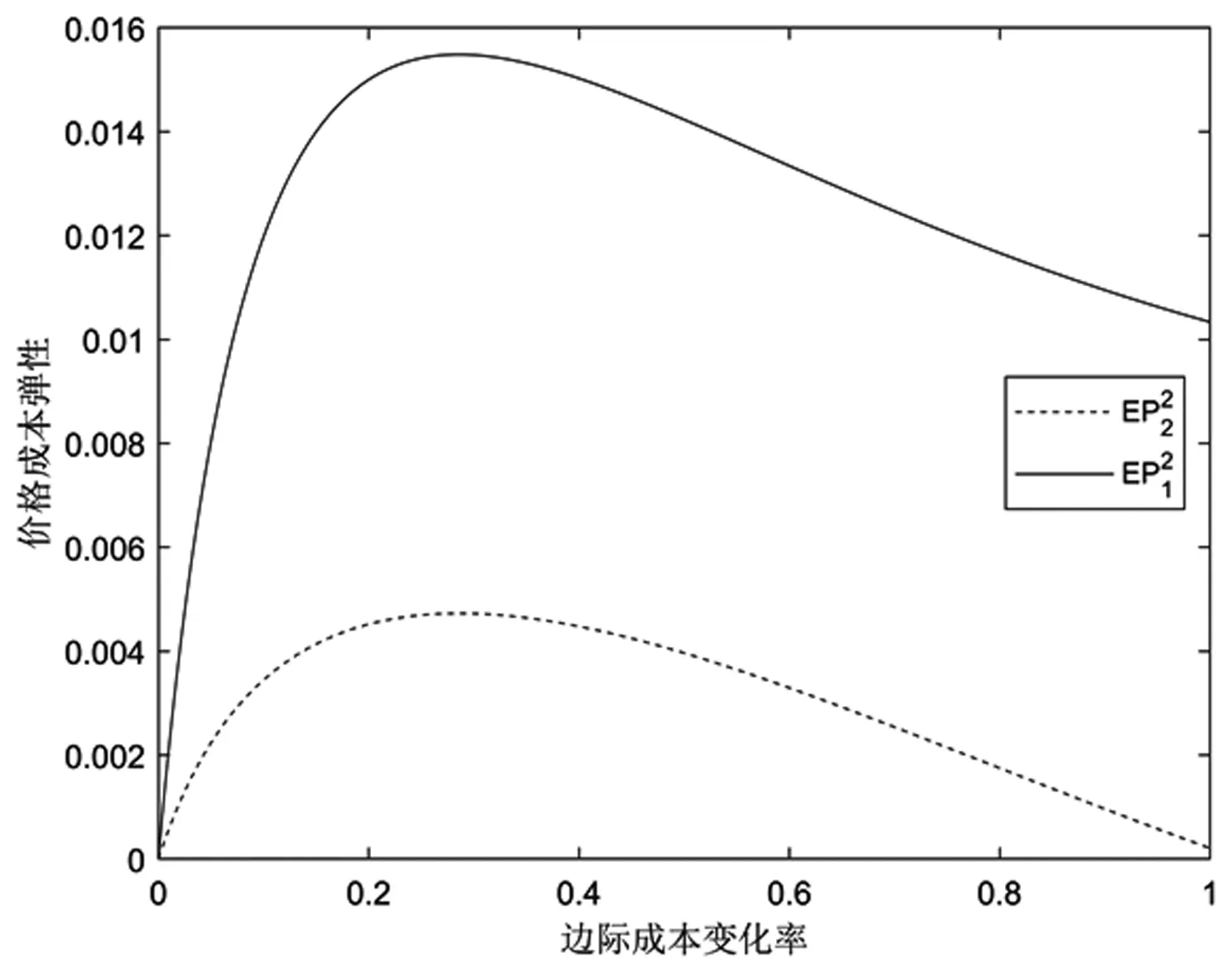
图3 价格的边际成本弹性图

图2中三条曲线分别代表产品质量为4000、5000、6000时，边际成本变化率与生产商利润的关系，可见无论如何选择质量，δ=0.1附近时，生产商利润增值最大，且质量值越大利润越高，然而当δ超过0.3时利润始终在下降，并且质量值越大利润下降越快。说明技术创新使得边际成本提高率不超过0.3时，可以带来更多利润，那么生产商选择创新，并且创新的同时促进了质量的提高。当技术创新使得边际成本提高率超过0.3时，利润减少，并且质量越好利润减少越快，生产商宁愿选择不创新。可见，生产商更倾向于低成本创新，且低成本创新促进产品质量的提高。

4 结束语

本文从理论上给出了没有任何产能约束时，随机需求下的技术创新边际成本的变化对生产商利润的影响，从而得出企业更愿意选择低成本创新的结论。结论表明，当边际成本提高超过30%时，由于成本过高得不到更大利润，甚至会利润下滑，企业宁愿选择不创新。

本文结论从数据上给企业技术创新策略提供了一定的依据，从技术创新后的产品价格上看，结论对高科技领域的企业更有针对性，若旧技术产品利润下降速度快，有退出市场的趋势，那么迫使企业必须创新。决策者可根据创新投入预测产品边际成本的变化率是否在合理范围内，或根据预期的变化范围来控制创新成本。

我们假设的价格函数中销量与价格呈反比，也就是说技术创新使得价格提高就必然导致销量下降，这也是此模型的不足之处，事实上，现实中的大部分产品的价格和销量并不是线性的，产品扩散会受到很多因素影响，比如，消费者的质量偏好、地域间收入水平的差异等等。在以后的研究中，可以考虑在模型中加入消费者效用函数，其受产品质量和价格、零售店服务水平、便捷性等因素影响，从而使得模型更接近现实情况。