Six sigma robust design optimization for thermal protection system of hypersonic vehicles based on successive response surface method
Jingjing ZHU, Xiojun WANG,*, Higuo ZHANG, Yuwen LI,Ruixing WANG, Zhiping QIU
a Institute of Solid Mechanics, School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China
b The 704 Research Institute of CSIC, Shanghai 200031, China
c Institute of Mechanics, Chinese Academy of Science, Beijing 100190, China
KEYWORDS Hypersonic vehicle;Six sigma robust optimization;Successive response surface;Thermal protection system;Uncertainty
Abstract Lightweight design is important for the Thermal Protection System(TPS)of hypersonic vehicles in that it protects the inner structure from severe heating environment.However,due to the existence of uncertainties in material properties and geometry,it is imperative to incorporate uncertainty analysis into the design optimization to obtain reliable results. In this paper, a six sigma robust design optimization based on Successive Response Surface Method (SRSM) is established for the TPS to improve the reliability and robustness with considering the uncertainties.The uncertain parameters related to material properties and thicknesses of insulation layers are considered and characterized by random variables following normal distributions. By employing SRSM, the values of objective function and constraints are approximated by the response surfaces to reduce computational cost.The optimization is an iterative process with response surfaces updating to find the true optimal solution.The optimization of the nose cone of hypersonic vehicle cabin is provided as an example to illustrate the feasibility and effectiveness of the proposed method.
1. Introduction
The Reusable Hypersonic Vehicle (RHV) is a fully reusable transportation system that operates at hypersonic speed(Ma >5)for a significant part of its trajectory.During reentry into the atmosphere at hypersonic speed,one of the main challenges is that the RHV is subjected to severe aerodynamic heating upon the surfaces which are exposed to the surroundings, especially, the harshest heating environments locate on the nose of the vehicle and the wing leading edges due to the stagnation point heating. In order to successfully achieve hypersonic flight, a Thermal Protection System (TPS) is designed to protect the inner structures of hypersonic vehicles from extreme temperature. The research into thermal protection technology is ongoing and becomes a hot issue.1-3
In order to make hypersonic vehicles more durable, operable and cost effective,the current design of TPS is mainly carried out to realize the minimum weight and better insulation performance by defining the material, arrangement and thickness.4-6For instance, Garcia and Fowler7used a first-order optimization algorithm to minimize the weight of the TPS for reentry space shuttle. Shi et al.8investigated the optimization design of TPS formulated with mass per unit area of the TPS as the objective function considering the relationships of multi-discipline in the TPS. Xie et al.9investigated the weight optimization for a corrugated sandwich panel which served as an Integrated Thermal Protected System (ITPS). Normally,these existing studies were carried out under the assumption that all of the parameters involved in the heat transfer analysis were deterministic. However, due to the materials dispersion,manufacturing process constraints and operating condition deterioration of production stages,the presence of uncertainty in material properties and geometry is intrinsic and it markedly affects the temperature response of TPS. The uncertainty of temperature response is significant to the design of TPS in which even a few degrees of temperature variability may cause serious consequences.10Sachin and Mahulikar11pointed out that there were physical complexities and uncertainties associated with the analytical models which were used for TPS performance. It is critical to consider these variations during the optimization, in order to ensure the safety of the final design and the performance constraints even in the presence of uncertainty. Wright12and Ravishankar et al.13proposed the uncertainty analysis approaches by using Monte Carlo method for probabilistic sensitivity and uncertainty propagation analysis of TPS material responses. Therefore, it is requisite to include uncertain analysis into the design optimization for TPS.
Traditional deterministic optimization considers the uncertainties through the use of empirical safety factors based on experience. This practice often leads to over-designed products.It cannot provide insights into the actual margin of safety of a design, and the effects of individual uncertainties cannot be distinguished either. Therefore, uncertainty-based design methods,which combine optimization approaches with uncertain analysis,14-17have been developed in recent years. The uncertainty-based design generally includes structural reliability design,18,19robust design,20,21etc. The structural reliability design converts the deterministic constraints into reliability constraints by reliability analysis. The reliability analysis evaluates the probability of failure or reliability index of the design with respect to specific structural performance constraints.The uncertainty-based analysis and optimization design for TPS is promising, yet insufficient up to now. Some researchers have made a few attempts in this field. Kolodziej and Rasky22used the non-dimensional load interference method for estimating thermal reliability from an assessment of TPS uncertainties.Kumar et al.23investigated the probabilistic optimization of ITPS that combines the thermal protection function with the structural load carrying function. Antonio and Marchetti24presented a statistical methodology based on the Monte Carlo method to perform a size optimization of an ablative thermal protection system for atmospheric entry vehicles.However,the objective of the reliability-based optimization is evaluated at the mean value point. The design only accounts for the shift of the mean values of responses from constraint boundaries,but not considers the size of the response distributions and the possibility of reducing the variation of response.
Recently,the six sigma robust optimization has been widely applied to quality engineering.25-27Six sigma robust optimization is an advanced design method combining six sigma quality management theory and robust optimization, which aims to minimize the objective and satisfy the reliability design requirements. The six sigma robust optimization considers both the optimality and robustness of the objective to achieve lower sensitivity of objective performance to the uncertainties.Many scholars have carried out a lot of studies in this field. Roger et al.28proposed a conceptual definition and underlying theory of six sigma based on the grounded theory and previous literature available. Patrick et al.29presented a six sigma based probabilistic design optimization formulation that combined the structural reliability and robust design with six sigma philosophy.He pointed out that design quality came at a cost and the tradeoff between the optimization objective and the reliability (or sigma level) should be considered in the design. On the basis of the ‘‘Design For Six Sigma” (DFSS), a new method ‘‘Design For Multi-Objective Six Sigma (DFMOSS)”that combined the theory of DFSS and Multi-Objective Evolutionary Algorithm (MOEA) was presented.30,31In order to improve both the reliability and robustness of the design, this paper proposes a six sigma robust optimization model to carry out a probabilistic optimization for the TPS of hypersonic vehicles.
In the transient heat transfer analysis for TPS along the entire trajectory, the Finite Element (FE) analysis needs to be continued for long time to capture the peak temperature,which seriously reduces the efficiency of optimization. Since the optimization process for TPS needs plenty of repeated individual FE simulations, the computation may be extremely expensive for broad design space. Moreover, probabilistic analysis and reliability-based optimization will further increase the computation cost and the fact that TPS components are generally made of composite materials further increases the uncertainties in material properties.13To reduce the computational cost, many approximation models were put forward to generate surrogates of the FE simulations. The sampling data are chosen by Design of Experiment (DOE) and the surrogate models can be utilized for optimizations as substitutes of FE simulations. There are many types of surrogate models, such as Kriging model,32Neural Networks model,33Response Surface Approximation (RSA),34-37etc. As the form of an approximate function is assumed first, the Response Surface Method (RSM) often serves as an effective statistical method.It uses fewer resources and quantitative data to solve a multivariate optimization problem. Theodore et al.38utilized RSM to achieve the deterministic and reliability optimizations for the integrated cryogenic propellant tank of a reusable launch vehicle.Ravishankar et al.13studied the uncertainty characterization and predicted the probability of failure for an ITPS by using RSAs. The accuracy of response surface approximation has a great influence on the optimal solution. In some cases,though the quality of the approximation is acceptable across the entire design space, the error near the design point may be high resulting in a poor optimum design. In the past decades,many methods have been actively studied to improve the accuracy and computational efficiency of RSM for optimization problem, one of which is the Successive Response Surface Method (SRSM).39Generally, the smaller the design space is, the greater the accuracy of approximation will be.In addition,the researchers have developed other methods that can iteratively improve the accuracy of the response surface modeling. Kim and Na40proposed an improved sequential response surface method to evaluate the reliability inherent in nonlinear functions. Giunta et al.41utilized the variablecomplexity response surface modeling method to reduce the design space for the region of interest, which has been widely used in structural designs. Wang42presented an improved Adaptive Response Surface Method(ARSM)with global convergence and high optimization efficiency for high-dimensional design problems. Therefore, this paper employs the successive response surface method during the six sigma robust optimization process to improve the accuracy of response surface,which is rare in the field of TPS optimization considering uncertainties to the author's knowledge.
In this paper, an efficient and effective optimization approach obtained by coupling six sigma design, TPS thermal analysis and SRSM is proposed to carry out a probabilistic optimization for the TPS of hypersonic vehicles. The TPS model used in this paper is a typical structural component of the hypersonic vehicle. The presented method will provide more reliable and robust design for the TPS while considering the effects of uncertainties on the structural responses,and the computation cost will be reduced significantly. The remainder of this paper is organized as follows. Section 2 describes the configuration of the TPS model of a typical hypersonic vehicle and the governing equations of heat transfer analysis. The deterministic optimization model and six sigma robust optimization model for the TPS are established in Section 3. In Section 4, the optimization approach based on SRSM is presented and the complete strategy procedure of this paper is elaborated. In Section 5, a model of the nose cone of a hypersonic vehicle cabin is used to illustrate the application of the proposed methodology.Finally,some conclusions are summarized in Section 6.
2. Configuration and governing equations of TPS
2.1. Description of TPS configuration

Fig. 1 Depiction of TPS configuration of a hypersonic vehicle.
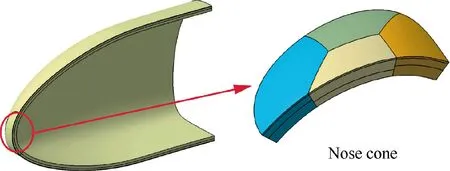
Fig. 2 Multi-blocks structure of TPS.
The TPS is attached to the outer surface of the hypersonic vehicle structure, such as the vehicle cabin as depicted in Fig.1.The TPS modeled in this paper consists of three layers,i.e. an external panel and two insulation layers, which are bonded together with adhesive. The external panel serves as a heat shield, which insulates the insulation layers from external ambient to protect the insulation layers from the damage due to high temperature and aerodynamic pressure.The material used for the first layer should be capable of withstanding high temperature and the second layer is filled with the material that has prominent insulation capacity at the relatively lower service temperature.43Generally, the thickness of the external panel is much smaller than those of insulation layers.
In practical engineering, the TPS generally adopts the multi-blocks structure (see Fig. 2), namely the whole TPS is divided into several blocks, one of which is connected to another by fastener,and the gap is filled with sealing materials.Actually, the thicknesses of the insulation layers of different blocks can be inconsistent with each other due to the complex thermal environment.
2.2. Transient heat transfer analysis for TPS

Fig. 3 Loads and thermal boundary conditions imposed on the outer surface of TPS.
The loads and thermal boundary conditions imposed on the outer surface of TPS are shown in Fig. 3. A large portion of heat is radiated out to the ambient by the outer surface. The inner surface of the second insulation layer is assumed to be perfectly insulated.That is to say,the heat convection between the TPS and the interior of vehicle is not considered.With this assumption, the optimization would lead to a conservative design.Radiation and convection through the insulation material are ignored and only the conduction is taken into consideration.The initial temperature of the whole model is assumed to be a constant at the start of reentry. Besides the above assumptions, the effect of the adhesive on heat transfer is ignored and the interfaces between adjacent layers of TPS are assumed to be perfectly conductive, which indicates that there exists no thermal contact resistance. Furthermore, since the gap between two blocks is filled with insulation materials with low thermal conductivity, the interfaces of different blocks are assumed to be adiabatic.
The basic governing equation of heat conduction can be described by the following partial differential form
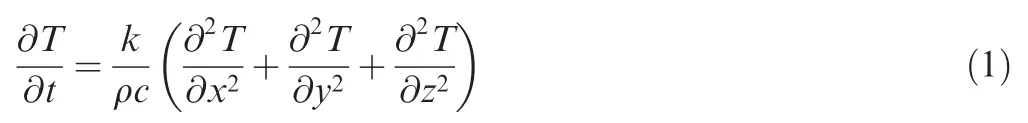
where T is the temperature, t is the time, K, ρ, c denote the thermal conductivity, density, and specific heat, respectively,x, y and z denote the coordinates along x-, y- and z-axes,respectively.
The initial condition for the thermal analysis is

where T0is the initial temperature and assumed to be 300 K in this paper.
The incident heat flux entering the TPS can be expressed as

where qinis the incident heat flux, n denotes the normal direction of the outer surface s.
The radiation to ambient is determined by

where qrstands for the radiation heat flux, ε is the surface emissivity of the outer surface which typically has a value of 0.8-0.85,44σ is Stefan-Boltzmann constant, Tsdenotes the temperature of outer surface and Tadenotes the ambient temperature.
Based on the surface energy balance condition, the boundary imposed on the outer surface yields

where qwis the heat flux load caused by aerodynamic heating.
After aircraft touchdown,a natural convection to the ambient is used as the boundary condition imposed on the outer surface (see Fig. 3)

where qcrepresents the convection heat flux, α is the convection coefficient.
3. Deterministic and six sigma robust design optimization for TPS
3.1. Deterministic optimization for TPS
The TPS will not only fulfill the required thermal protection functions, but also must be as lightweight as possible to minimize operational costs. In this section, an optimization model is defined to determine the optimal thicknesses of insulation layers aiming at minimizing the total weight while maintaining the structures with acceptable temperature limits. The design variables for the optimization are the thicknesses of insulation layers of the TPS, which can be denoted by a vector d. Two critical constraints are considered for the optimization to guarantee the functions of TPS and underlying structures: (A) the maximum temperature of each insulation layer must be less than the service temperature limit of the insulation material and (B) the maximum temperature of the inner surface of TPS must be less than the critical temperature that is safe for the underlying structure/screw compartment of the vehicle.The optimization problem of the TPS can be described mathematically as follows:


3.2. Six sigma robust design optimization for TPS
In practice, the solution obtained by deterministic optimization is often close to the critical constraints, which will result in an unreliable design due to the fluctuation existing in input parameters or environment. Reliability-based optimization focuses on the effects of random design variables, in which the optimal solution is shifted away from constraint boundaries to improve design reliability. To shrink the performance variation, robust design is implemented to decrease the sensitivity of design response to uncertainties. By combining reliability-based optimization,robust design and six sigma philosophy, Design For Six Sigma (DFSS)29,30,45is proposed to improve design quality, as illustrated in Fig. 4. In ‘‘shift”,the performance distribution is shifted until an acceptable level of reliability(area of distribution inside constraint)is achieved.In‘‘shrink”,the performance variation is shrunk to reduce the potential performance loss associated with the tails of the distribution and thus reduce the sensitivity and improve the robustness. In ‘‘shift+shrink”, with both shift and shrink,the reliability level is achieved and the robustness is improved.
The one consistency between the measures of reliability and robustness is the measure of variation: sigma. The performance variation can be characterized as ‘‘sigma level n”, as illustrated in Fig. 5. The areas under the normal distribution associated with each σ-level relate directly to the reliability(e.g. ±1σ is equivalent to a reliability of 68.26%). Larger σlevel indicates smaller variation,i.e.more robust characteristic.The DFSS is proposed to achieve 6σ quality, which is defined to maintain six sigma μ±6σ( ) performance variation within the specification limits.

Fig. 4 Improvement of reliability and robustness.
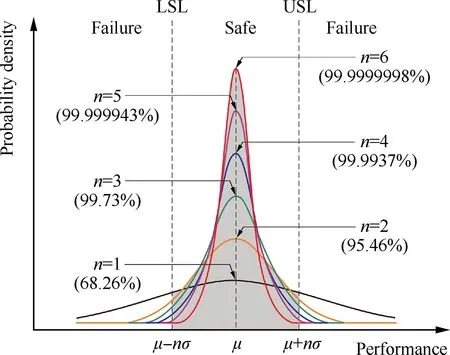
Fig. 5 Characteristic of sigma level n (LSL: lower specification limit, USL: upper specification limit).
To improve the reliability and robustness,the deterministic optimization for TPS is converted to a six sigma robust design optimization by considering the uncertainties related to the geometric parameters and material properties. The six sigma robust optimization is established to minimize the mean and variation of performance response with constraints imposed on the input variables and output responses. The input constraints are random design variable bounds and the output constraints can be reliability or sigma level quality striving to maintain performance variation within the defined acceptable limits. The formulation can be expressed as follows:

where μ and σ denote the mean value and standard variation of structural weight or temperature constraint which are functions of the design variables and random input variables, λ1and λ2are the weight coefficients for the mean and standard variation of structural weight, dLand dUare the lower limit and upper limit of design variable vector, respectively. The principle of six sigma robust optimization is illustrated in Fig. 6 which shows that the solution B obtained by six sigma robust optimization has higher reliability and robustness as a comparison with the solution A obtained by deterministic optimization.
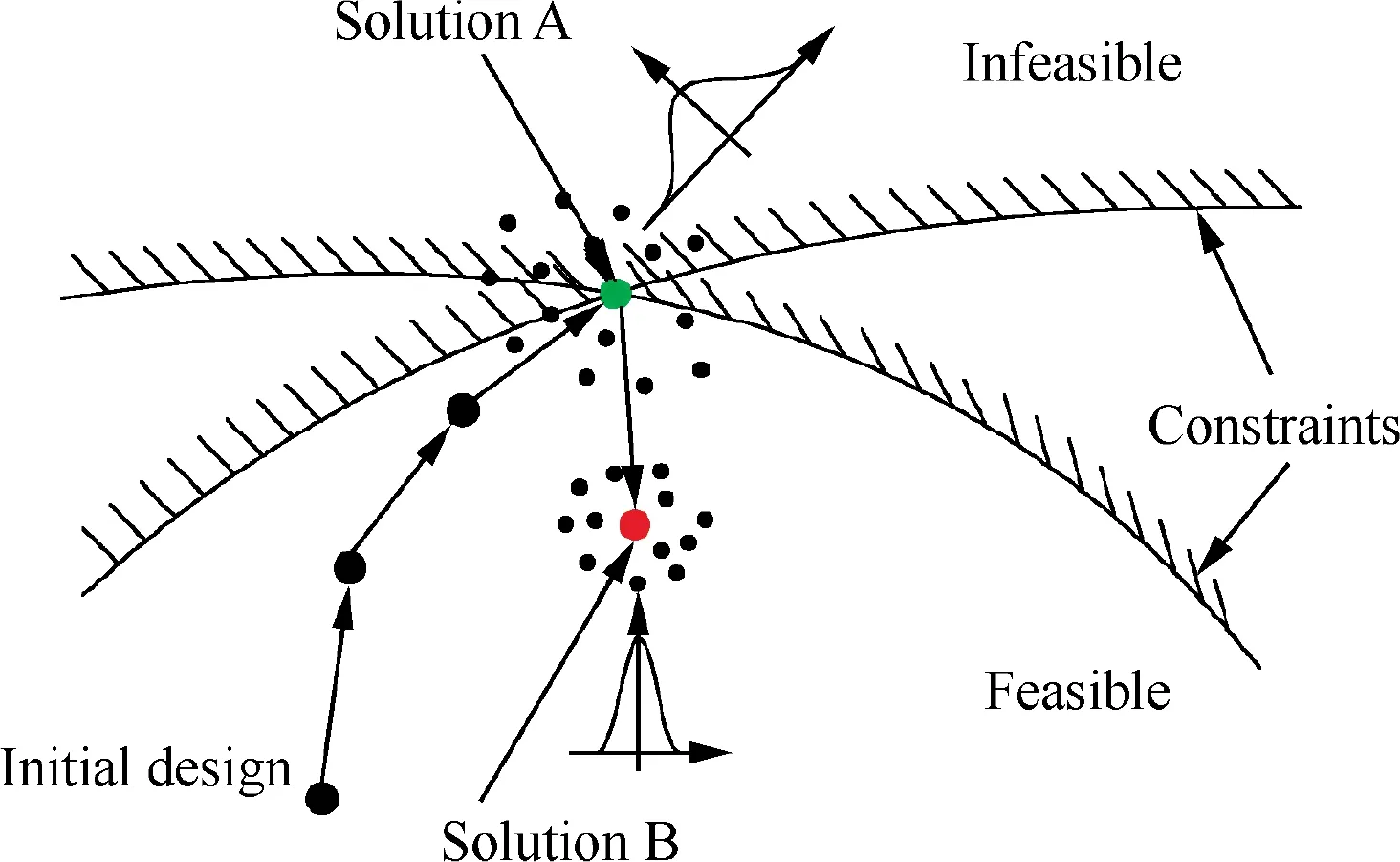
Fig. 6 Principle of six sigma robust design.
4.Successive response surface method based design optimization
In this paper, the vehicle is subjected to time varying aerodynamic heating load in the course of flight trajectory.As shown in Fig.7,the TPS was heated up by the heat flux load before t0in the trajectory. After t0, the aerodynamic heating ends but the temperature of TPS will continue to rise due to the heat transfer along the thickness direction. Consequently, the thermal analysis of TPS needs to be continued for long time to capture the peak temperature. For the probabilistic analysis and optimization with considering the uncertainties, it would require numerous simulations to study the uncertain propagation which may be extremely expensive for broad design space.In addition, the complexity of the solid model of the TPS of hypersonic vehicles will also lead to high computational expense. Therefore, the computation cost will be unbearable if the analysis was carried out by FE simulation.

Fig. 7 Temperature profile of TPS with time.
4.1. Construction of response surface approximation
In this work, quadratic RSAs are used to construct the objective and constraints as functions of input parameters,since it is simple, easy to implement and has reasonable accuracy for concept and preliminary design of structure.5During optimization process, the quadratic response surfaces of objective function and constraints are constructed as follows:
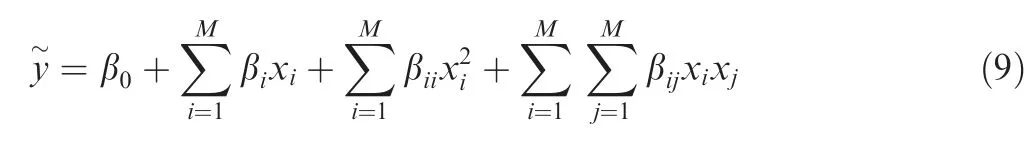
Before constructing the RSA, a DOE should be implemented to locate the sampling points in the design space. In this paper, the Optimal Latin Hypercube (OLH) is chosen for DOE because of its low computational cost and uniformity of samples resulting in better approximations.46
4.2. Successive response surface method
In the optimization procedure, the estimations of output responses are implemented by RSM. Generally, the quality of the approximation is evaluated by separate data set or cross-variation to ensure that the approximation has an acceptable average error across the entire design space. However, the error near the design point may be high resulting in a poor optimum design.Therefore,the response surface updating is needed in the optimization process to obtain a design with a higher probability of success.
In order to ensure the solution converge to the true optimum, the accuracy of RSA is improved by reconstruction via adding additional sampling points from the new subregion centered around the optimal solution into the previous sampling data set.The subregion is updated by shift and reduction from the previous one,as shown in Fig.8.Moreover,the optimal point serves as a starting point for the next iteration during optimization procedure. The bounds of the i-th design variable for the k+1-th subregion can be determined by



where η=0.5 and γ=1.0 for quadratic approximations39in this study. In addition, γ are chosen as γ=0.8 for linear approximations in order to counter the cycling effect as commonly encountered when using successive linear approximations.
The convergence criterion used in this research is the relative change in the approximate objective values in the last two iterations which can be expressed by

where ε is the convergence control parameter and its value is considered as 0.001,G dk( )and G dk+1( )denote the approximations of the objective for the k-th and k+1-th iterations,respectively.
Fig. 9 illustrates the optimization process based on SRSM and the detailed computational procedure can be summarized as follows:
Step 1.The first RSA denoted by1is established by DOE for the initial design space.Then the RSA is used to obtain the optimal point d1by optimization procedure. From Fig. 9, it can be seen that there is a relatively large deviation betweenand the actual response y around d1. Therefore, the accuracy of RSA around d1needs to be improved to obtain the actual optimal solution.
Step 2.The optimal point d1is used as the new center point to construct a subregion, in which M additional sampling points are created and added into the previous sampling data set.

Fig. 8 Updating of subregion for RSA reconstruction.

Fig. 9 Optimization process based on SRSM.
Step 4.By the same way, the processes of RSA reconstruction and optimization are repeated until the convergence condition is satisfied and the final approximate optimal solution dfinalthat is very close to the actual solution dactualcan be obtained.
4.3. Strategy procedure
In this subsection, we will elaborate the design procedure of the deterministic optimization and six sigma robust optimization for the TPS of hypersonic vehicles as follows:
Step 1.Initialize design variables.The geometric parameters are selected as the design variables for this optimization and their nominal values are defined as the initial values.
Step 2. Create RSA. To reduce the computation cost, the RSAs are created to evaluate the output responses, including objective function and constraints. The sampling points of input parameters, including design variables and random parameters, are generated by using OLH.
Step 3. Construct and solve deterministic optimization problem. Construct the deterministic optimization and the model can be mathematically written as Eq. (7). The overall weight of TPS is set as the objective function to be minimized and the critical temperatures of insulation layers and inner surface are considered as the constraints that maintain the functions of TPS and underlying structure of vehicle.
Step 4. Update RSA. The RSA will be updated in the optimization process to improve the analysis precision. The optimal solution is employed as the sampling center to construct additional sampling points, which is used to create a new RSA along with existing sampling points.If the relative change in the approximate objective values in the last two iterations is less than ε, turn to Step 5, otherwise, turn back to Step 3 to repeat the optimization process.
Step 5. Perform quality analysis. To analyze the quality of design, the quality of the deterministic optimum solution is measured by six sigma analysis to obtain the reliability or sigma level of the design.
Step 6. Establish six sigma robust optimization model. To improve the quality of design, the deterministic optimization is converted into a six sigma robust optimization formulated as Eq.(8). The objective is to improve the robustness by minimizing both mean value and standard variation of the performance response. The constraints are reformulated as quality constraints which satisfy six sigma level. The six sigma robust optimization starts with the deterministic optimal solution.
Step 7. Update RSA. After the initial optimal solution is obtained, the RSA will be updated by the same way used in Step 4.
Step 8. Obtain optimal solution. Conduct Step 6 to Step 7 until the convergence condition is satisfied and the optimal solution can be obtained.
The flowchart of the optimization procedure is shown in Fig. 10.
5. Demonstrative example
5.1. Thermal analysis
The nose cone of a typical hypersonic vehicle cabin(see Fig.2)is selected as the application to demonstrate the effectiveness of the proposed optimization strategy. Since the thickness of external panel is much smaller than that of insulation layer,it is not chosen as the design variable and is held at a constant value of 5 mm. For simplicity, the thicknesses of the first or second insulation layer of all blocks are assumed to be the same. Therefore, the geometric parameters to be optimized include:the thickness of first insulation layer h1and the thickness of second insulation layer h2with initial values of 22 mm and 32 mm, respectively. The material properties of the panel and insulation layers,including thermal conductivity k,specific heat c, density ρ, are listed in Table 1.
To properly represent the heating trend along the entire trajectory,55 points are selected from the trajectory and the time interval between adjacent points is 20 s.The heat flux imposed on the TPS and ambient temperature are schematically illustrated in Fig. 11, which are obtained from a real flight test.As shown in Fig. 11, the incident heat flux load is imposed on the outer surface before 1100 s (reentry phase) and there is no heat input after 1100 s (landing phase). As discussed in Section 2, the outer surface of TPS has radiation boundary condition during reentry and convective heat loss is also applied after landing.The radiation is determined by the emissivity ε of the outer surface with a value of 0.85 and the convection coefficient α is assumed to be 6.5W/ m2·K( ).43The maximum temperature responses of the external panel and insulation layers are calculated by commercial software ANSYS and the finite element model is shown in Fig. 12.Due to the symmetry of the structure, thermal loads and boundaries, only half the model is built for calculation.
After landing,the transient heat transfer analysis continues another 5400 s to capture the peak temperatures. The detailed results are depicted in Fig. 13, which illustrates the maximum temperature profiles of external panel, insulation layers and inner surface with time. It shows that the temperatures of external panel, insulation layers and inner surface increase because of aerodynamic heating during reentry process. The external panel reaches its peak temperature rapidly at about 620 s with a value of 1752.77 K and the maximum temperature of the first insulation layer reaches at 620 s with the same value as well.After 1100 s,there is no heat flux loading anymore,but the inner surface will continue to be heated up caused by the heat transfer along the thickness direction.The peak temperature Tinner,maxis reached at about 5800 s with a value of 411.72 K and then begins to decrease slowly.

Fig. 10 Flowchart of the optimization procedure.

Table 1 Material properties of panel and insulation layers.
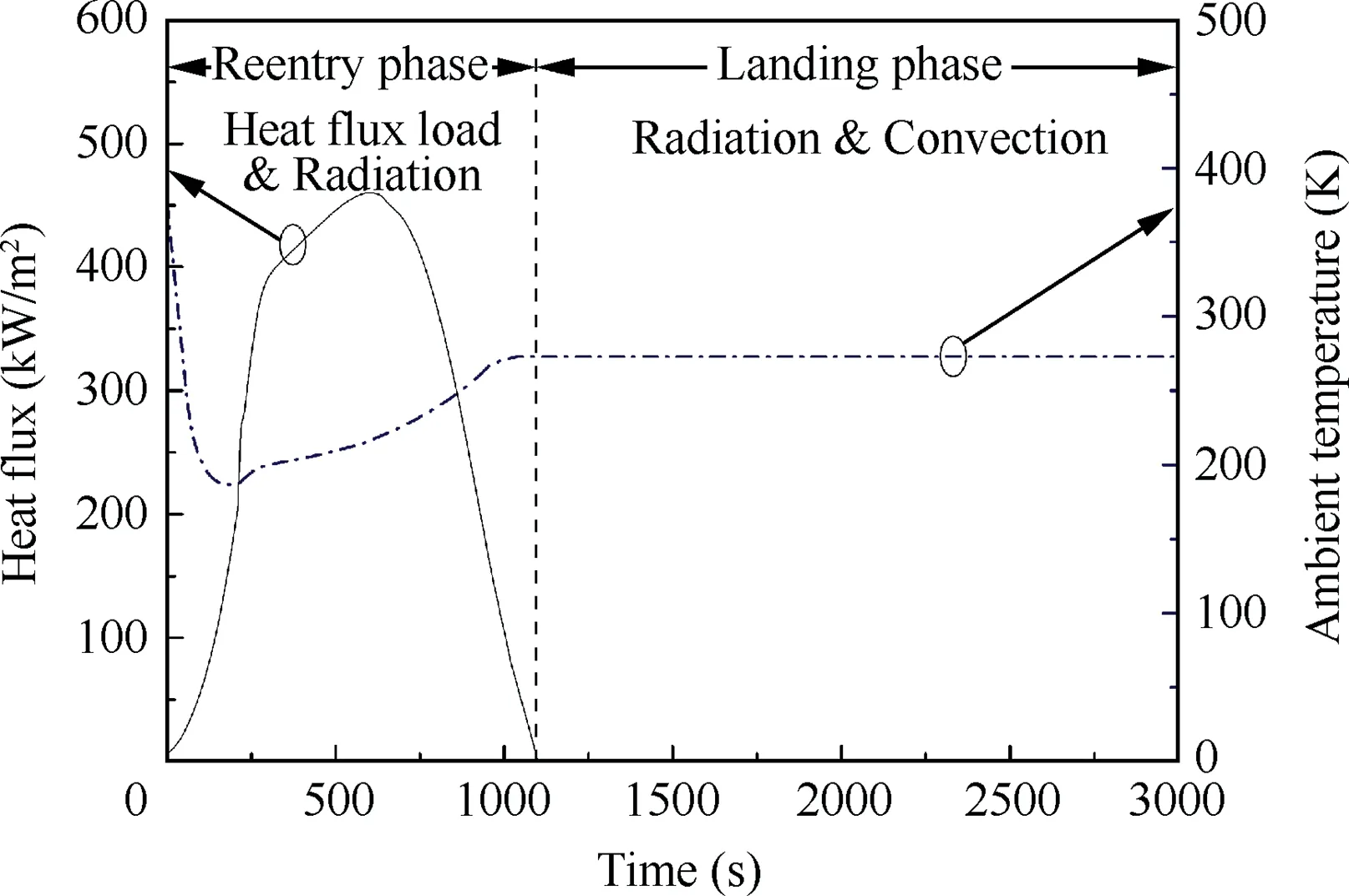
Fig. 11 Heat flux load and ambient temperature.
5.2. Construction of RSA

Fig. 12 Finite element model of the nose cone.
Form Fig. 13, it can be seen that the finite element analysis needs to continue for long time to obtain the maximum temperature of inner surface, which leads to high computational cost. The quadratic response surfaces of finite element model are built to express the relationships between input variables(including design variables and random parameters)and target responses,as a way to reduce the computation cost in the optimization process.Since we focus on the maximum temperature of TPS during the entire trajectory rather than the local temperature at a fixed point, the response surfaces of the maximum temperatures of TPS's FE model are constructed to approximate the relations between the input parameters and temperature constraints.DOE method is used to generate sampling points for RSA construction. By considering the uncertainties in material properties, the following eight parameters(listed in Table 2)are defined as random variables.The design variables h1,h2are also selected as random variables with coefficient of variation of 0.02.

Fig. 13 Temperature profiles of the maximum temperatures of external panel, insulation layers and inner surface.
The sampling data set for DOE will be created by OLH with variations of 6σ around the random variables and the design space of design variables are given in Table 3.
The total number of input parameters is 8 and the quadratic (second order) response surfaces are used in this paper.Accordingly, the minimum number of sampling points is 8+1( ) 8+2( )/2=45. Therefore, a sampling data set of 45 points is used to generate the first response surfaces. The predicted values of 20 error analysis sampling points are compared with the actual values obtained by finite element analysis, as depicted in Fig. 14. The error estimates of the response surfaces are given in Table 4 to illustrate the accuracy of RSA. From Fig. 14 and Table 4, we can see that the predicted values accord with the actual values across the entire design space.
In engineering practice,the uncertainty of composite material properties will increase, which may be much greater than 0.02.The increase in the uncertainty of material properties will lead to larger design space for DOE to construct the response surface. To solve the problems with large uncertainty level,more sampling points should be generated or some other DOE methods such as central composite design47and improved LHS48could be employed to obtain desirable response surface approximation.
5.3. Deterministic optimization
The TPS is first optimized deterministically to identify a feasible design from which to begin six sigma robust optimizationfor quality measurement and improvement. The TPS is to be designed for minimum weight subject to constraints on the maximum temperatures of each insulation layer and inner surface.The values of the uncertainties are set to be the mean values. To find the optimal thicknesses of the insulation layers,the ranges of the thicknesses are assumed as h1=10 to 30 mm h2=20 to 40 mm

Table 2 Random variables in material properties.

Table 3 Design space of design variables for DOE.
The temperature limits of the insulation layers and inner surface are 1800 K,720 K,473 K,respectively.The RSAs constructed in Section 5.2 are used to evaluate the objective function and constraints during the optimization process.
This study uses the NLPQL method to obtain the optimal solution. The parametric modeling is carried out by CATIA and thermal analysis is conducted by ANSYS.The integration of these two modules is achieved by iSIGHT. The optimal solution is listed in Table 5 and the actual values of objective function and constraints at the optimal point obtained by Finite Element Method(FEM)are also given.We can see that there are large deviation between the values of constraints obtained by RSA and FEM,especially for Tinner,max.Therefore,the response surfaces constructed in Section 5.2 will be updated by SRSM to improve their accuracies around the optimal point. The optimization history using SRSM is given in Table 6.For each iteration,n=8(the number of input variables) sampling points generated from subregion are added into the previous sampling data set to reconstruct a new RSA. As seen in Table 6, the optimal solution converges after 5 iterations with optimum values of h1=15.301 mm and h2=27.136 mm, resulting in a weight reduction of 13.5%.
However, this design has two active constraints: the maximum temperatures of the second insulation layer and inner surface. To analyze the quality of the deterministic design,the six sigma analysis is performed at the optimal solution with consideration of the uncertainties existing in material parameters(see Table 2)and design variables h1,h2.By means of RSA,the six sigma analysis will be implemented by Monte Carlo method. The quality results are given in Table 7 alongside the deterministic optimization solution, in which Rel. denotes Reliability.

Fig. 14 Comparison between predicted values and actual values.

Table 4 Error values of RSAs (Root mean square).
As Table 7 indicates,the quality of deterministic design has 0.686σ level and reliability of 50.70% for T2,max, and 0.643σ level and reliability of 48.01% for Tinner,max. The probability distributions of active constraints are displayed pictorially in Fig.15.From Fig. 15,the overall quality or sigma level is different from the sigma position of the upper bound.For example,with a single upper bound at 0.017σ as shown in Fig.15(a),the percent of the distribution variation outside the constraint is equivalent to that with symmetric lower and upper bounds at±0.686σ around the mean,and thus the overall quality level is 0.686σ.It can be observed that almost entire right half of thedistribution exceeds the constraint boundary. Obviously, the reliabilities of the active constraints are less than desirable values.

Table 5 Optimization results obtained by RSA and FEM.

Table 6 The deterministic optimization history based on SRSM.

Table 7 Quality analysis results of deterministic optimization solution.

Fig. 15 Constraints quality for deterministic optimization solution.
5.4. Reliability-based optimization

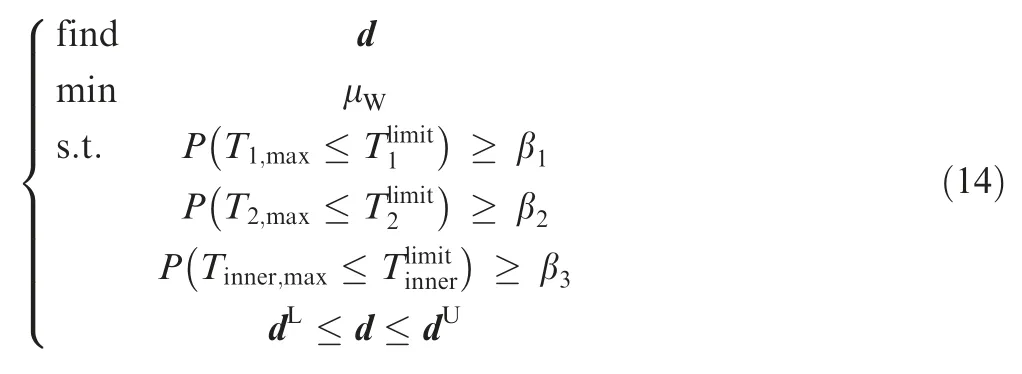
5.5. Six sigma robust optimization
In this subsection, the six sigma robust optimization is implemented based on response surface in this subsection.Similarly,the RSAs of objective and constraints need to be updated around the design point to acquire a higher accuracy by the method established in Section 5.2. The history of six sigma robust optimization based on SRSM is given in Table 9.

Table 8 Reliability-based optimization history based on SRSM.

Table 9 History of six sigma robust optimization based on SRSM.
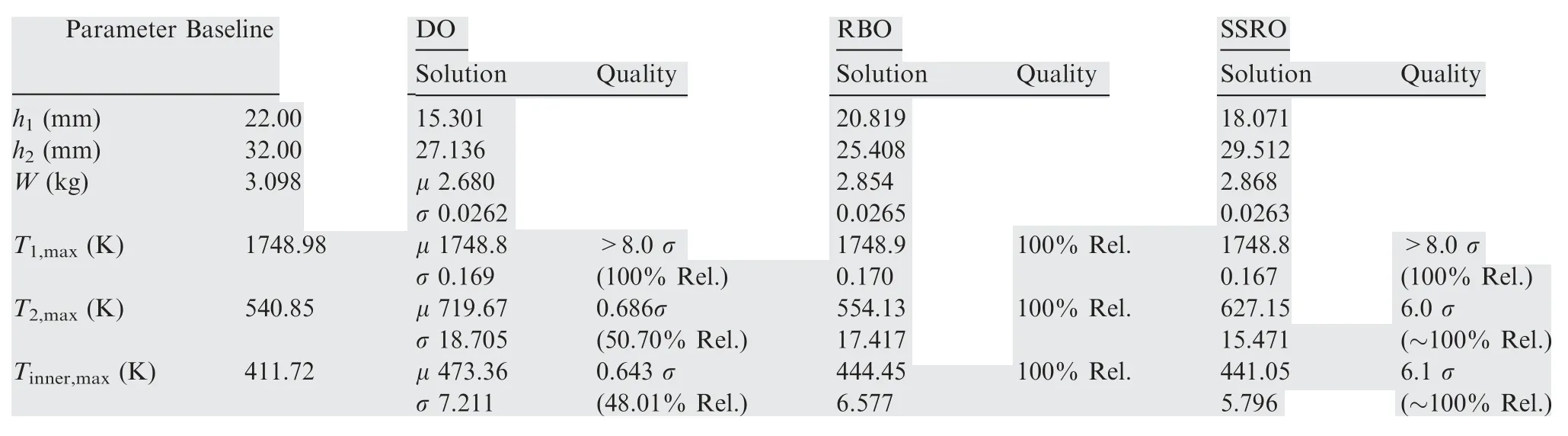
Table 10 Comparison between deterministic optimization, reliability-based optimization and six sigma robust optimization.
The comparison between the Deterministic Optimization(DO), Reliability-Based Optimization (RBO) and Six Sigma Robust Optimization (SSRO) is given in Table 10. From Table 10, compared with deterministic optimization, the quality level is increased for two active constraints by six sigma robust optimization. The sigma level is improved from 0.686σ to 6σ for the maximum temperature of second insulation layer and from 0.643σ to 6.1σ for the maximum temperature of inner surface. It means that the reliability is nearly 100%. For the reliability-based optimization, the mean value of the weight is μW=2.854 and the standard deviation is σW=0.0265. By means of six sigma robust optimization, the mean value of weight is 2.868 and the standard deviation is 0.0263, which is smaller than that from reliability-based optimization. Similarly, the variations of the temperature constraints, i.e. σT1,max,σT2,max, and σTinner,max, are also reduced by the six sigma robust optimization. Therefore, it can be concluded that the variations of objective and constraints due to uncertain parameters obtained by six sigma robust optimization are smaller than those obtained by reliability-based optimization, indicating that the former design is more robust.Based on the above discussions, compared with deterministic optimization and reliability-based optimization, the design quality including reliability and robustness is improved by six sigma robust optimization. Meanwhile, the trade-off of increasing the quality is an increase in weight. The weight is increased over the deterministic optimal solution, but is still less than the baseline design.
6. Conclusions
In this paper, a SRSM based six sigma robust optimization approach for the TPS of hypersonic vehicles is proposed to achieve the reduction of structural weight and improvement of design reliability and robustness considering the uncertainties in material properties and geometry. The transient heat transfer analysis for TPS is modeled along the data points selected from the entire trajectory to capture the peak temperatures of the insulation layers and inner surface of TPS.Based on the thermal analysis, the deterministic optimization model is established with the total weight of TPS as objective function and the temperature limitations of insulation layers and inner surface as constraints, to find the optimal thicknesses of insulation layers. By converting the objective to minimizing both the variation and mean performance, and reformulating the constraints as sigma level quality constraints, a six sigma robust optimization for the TPS is presented. In order to reduce computation cost, the quadratic RSM is employed to approximate the values of objective function and constraints.The SRSM based optimization combining response surface updating and optimization strategy is proposed to obtain the true optimal solution. The proposed optimization method is demonstrated in this paper for a nose cone of hypersonic vehicle cabin. The results show that, by using successive response surface in optimization process, the computation cost is reduced and the accuracy of RSA is improved.Compared with deterministic optimization and reliability-based optimization,the six sigma robust optimization notably improves the reliability and robustness of the design, which will have important guiding significance for the optimization design and safety of the TPS in practical engineering.
Acknowledgments
The paper was supported by the National Key Research and Development Program of China (No. 2016YFB0200700),the National Nature Science Foundation of China(No. 11872089, No. 11572024, No. 11432002), and Defence Industrial Technology Development Programs of China(No. JCKY2016601B001, No. JCKY2016204B101, No.JCKY2017601B001) for the financial supports.
 CHINESE JOURNAL OF AERONAUTICS2019年9期
CHINESE JOURNAL OF AERONAUTICS2019年9期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Heading control strategy assessment for coaxial compound helicopters
- An adaptive integration surface for predicting transonic rotor noise in hovering and forward flights
- An algorithm to separate wind tunnel background noise from turbulent boundary layer excitation
- Simulation of mass and heat transfer in liquid hydrogen tanks during pressurizing
- Leakage performance of floating ring seal in cold/hot state for aero-engine
- An active damping vibration control system for wind tunnel models
