圆轨道欠驱动航天器编队重构脉冲控制

钟都都，黄 煦,2，贾晓晓，金学敏

(1.中国人民解放军96901部队，北京 100094； 2. 清华大学 精密仪器系，北京 100084； 3. 中国人民解放军火箭军驻北京地区第七代表室，北京 100039； 4. 中国人民解放军96669部队，北京 102208)

0 引言

航天器编队飞行是空间任务中的一项关键技术，可应用于对地观测、在轨服务、深空探测等任务[1-3]。不同于传统单个大型航天器，航天器编队将以往单个航天器的功能分布在一群近距飞行的小型航天器内，因而具有低成本、低风险、高可靠性以及任务灵活性等优势[4-6]。其中，显著改善的任务灵活性得益于编队构型的可重构性，即编队内的航天器可根据不同任务需求通过相对轨道机动的方式改变航天器间的相对位置，从而改变编队的几何构型[7]。上述过程可定义为编队重构。作为编队飞行中的关键技术，编队重构控制成为研究热点与难点。

现有的编队重构控制方法可分为脉冲控制与连续推力控制方法。采用脉冲控制方法，VADDI等[8]设计了圆轨道编队最优重构控制方案。ROSCOE等[9]进一步考虑J2摄动，设计了摄动环境下圆轨道编队重构最优脉冲控制策略。此外，SOBIESIAK等[10]进一步对脉冲时刻进行了优化。对于连续推力控制方法，李静等[11]采用同伦分析方法和间接优化方法推导了连续小推力作用的燃耗最优重构控制轨迹。针对类似问题，吴宝林等[12]采用直接优化方法求解了最优控制轨迹。此外，滑模控制[13]、鲁棒控制[14]、神经网络控制[15]等方法也被应用于连续推力作用的重构控制方案设计。

然而，上述脉冲或连续推力控制方法均基于相对轨道动力学系统为全驱动控制系统的假设设计，即航天器径向、迹向和法向均存在独立的控制通道。若某一方向的推力器出现故障，系统成为欠驱动系统，即系统独立控制数目小于系统自由度的系统[16]。此时，上述全驱动控制方法均不再适用。显然，针对推力器故障问题，最为直接的解决方法为安装备份推力器[17]。但考虑到小型编队航天器的质量和成本约束，更为经济有效的方法为设计欠驱动控制器。

针对欠驱动重构控制问题，国内外学者已开展了一系列研究，主要包括径向欠驱动和迹向欠驱动两类控制方法。对于径向欠驱动控制方法，LEONARD等[18]基于航天器间的相对大气阻力近似作用于迹向的假设，提出了仅采用迹向相对大气阻力进行编队构型控制的概念。KUMAR等[19]采用线性反馈控制方法设计了圆轨道径向欠驱动编队重构控制器，且VARMA等[20]采用线性滑模控制方法解决了类似问题。对于迹向欠驱动控制方法，GODARD等[17]分析了迹向欠驱动条件下的圆轨道编队重构可行性，并基此设计了线性滑模控制器。随后，黄煦等[21]解析推导了两类欠驱动条件下的圆轨道编队重构最优解析，并基此设计了自适应控制器。然而，上述控制方案均假设控制器为连续推力，故而不适用于脉冲推力的控制方式。考虑到脉冲推力更易于工程实现，本文将研究脉冲推力作用下的圆轨道径向或迹向欠驱动编队重构控制方法。

综上，与现有成果相比，本文的不同与改进之处在于：1)与全驱动重构控制方法[7-15]相比，本文提出的控制方法可适用于径向和迹向欠驱动两类情况，故而可有效避免由推力器故障引起的重构任务失效；2)与现有全驱动重构控制方案相比，采用本文提出的欠驱动控制方案可有效减小控制器数目，进而减轻航天器系统质量，降低系统成本，更加符合未来小型化、低成本的编队航天器的发展需求；3)与连续推力作用的欠驱动控制方法[17-21]相比，本文提出的控制方法采用脉冲推力方式，故而更贴合工程实际，减少操作难度。

1 动力学建模与分析

1.1 动力学模型

坐标系定义如图1所示。由图可见，主航天器运行于圆轨道，从航天器飞行于主航天器附近，并与其构成编队。OEXIYIZI为地心惯性坐标系，OE为地心。主从航天器相对运动在轨道坐标系OCxyz中描述，其中，OC为主航天器质心，x轴沿主航天器地心距矢量RC方向，z轴沿主航天器轨道面法向，y轴与x、z轴构成右手笛卡尔直角坐标系。OD为从航天器质心，且RD为从航天器地心距矢量。

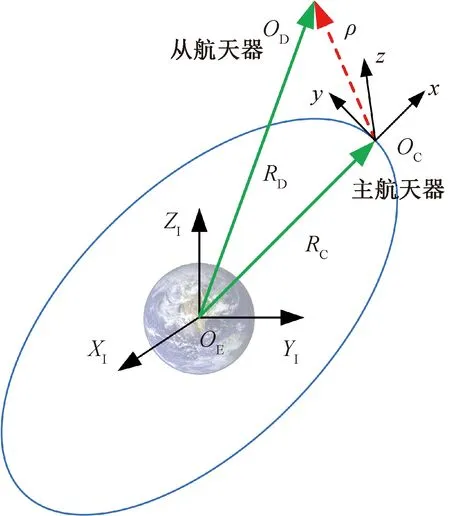
图1 坐标系定义Fig.1 Definition of coordinate frames

定义ρ=RD-RC=[xyz]T为主从航天器相对位置矢量，假设主从航天器相对距离远小于其地心距，则主从航天器相对运动方程可表述为[22]

(1)

其中

(2)

(3)

(4)

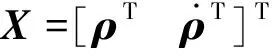
需要指出的是，上述线性化模型仅对近距航天器成立。一般地，对于相对距离在100 km范围的航天器，由线性化假设引起的误差不超过0.03%[23]。本文中讨论的航天器编队范围在几千米范围之内，因此，由线性化引起的误差可忽略不计。

1.2 能控性分析

主从航天器相对运动模型式(1)为线性时不变系统。根据线性系统理论[24]，系统(A,B1)在径向欠驱动条件下仍完全可控。相反，迹向欠驱动条件下，系统(A,B2)非完全可控，可按能控性结构分解为

(5)

其中

(6)

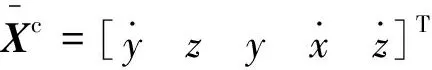
1.3 可行性分析

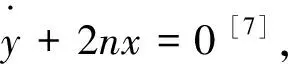
2 脉冲控制

如式(1)所示，对于近距圆轨道相对运动，平面内与平面外的相对运动状态解耦。同时，对于径向或迹向欠驱动情况，法向的相对运动与径向和迹向相对运动独立，且法向相对运动动力学系统为全驱动控制系统。因此，法向脉冲控制可采用常规全驱动脉冲控制方法设计，且对径向和迹向相对运动无影响。基此，本文仅对平面内的欠驱动脉冲控制方法进行设计，法向全驱动控制方法可参考文献[25]。

2.1 径向欠驱动

(7)

式中

(8)

式(7)的解析解为

(9)

式中：t0，tf分别为初始和终端时刻；ti为施加迹向脉冲的时刻。Φ1(τ2,τ1)为状态转移矩阵，即

(10)

式中：Δτ=τ2-τ1；s=sinnΔτ且c=cosnΔτ。Φ1v=Φ1(:,4)，即Φ1v为矩阵Φ1的第4列。

ΔX1=F1ΔV1

(11)

式(11)为k元一次方程组，其中，ΔX1∈R4，F1∈R4×k且ΔV1∈Rk，R表示实数域。显然，当k<4时，方程组无解；当k=4时，若rank(F1)=4，方程组有唯一解，其中rank表示矩阵的秩；当k>4时，方程组有无穷组解。由此可得，一般情况下，实现径向欠驱动编队重构脉冲控制的最小次数为4，并且当4次脉冲的时刻ti确定时，每次脉冲施加的速度增量ΔVyi也随之确定，即

(12)

2.2 迹向欠驱动

(13)

式中

(14)

同理可得，式(14)的解析解为

(15)

式中：Φ2v为状态转移矩阵Φ2(τ2,τ1)的第2列，即Φ2v=Φ2(:,2)；Φ2(τ2,τ1)的表达式为

(16)

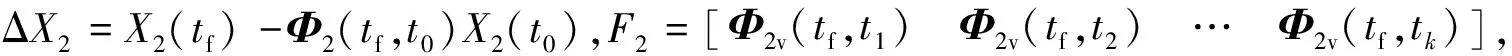
ΔX2=F2ΔV2

(17)

同理，式(17)为k元一次方程组，其中ΔX2∈R3，F2∈R3×k且ΔV2∈Rk。显然，当k<3时，方程组无解；当k=3时，若rank(F2)=3，则方程组有唯一解；当k>3时，则方程组有无穷组解。由此可得，一般情况下，实现迹向欠驱动编队重构脉冲控制的最小次数为3，并且当3次脉冲的时刻ti确定时，每次脉冲施加的速度增量ΔVxi也随之确定，即

(18)

3 数值仿真及结果分析

假设主航天器运行于轨道高度为500 km的圆轨道，初始时刻主从航天器构成半径r=0.5 km的投影圆编队，其几何构型表达式为[7]

(19)

式中：r为投影圆编队半径，且φ0为相位角。本算例中假设初始编队构型的相位角为0，即φ0=0。

选取待重构的构型为r=1.0 km且φ0=π/2的投影圆编队，且终端时刻选定为tf=T，其中T表示主航天器轨道周期。两类欠驱动情况下的仿真结果如下所述。

3.1 径向欠驱动

选取的4次脉冲时刻见表1。由式(12)计算得到的脉冲速度增量也总结于表1。可见，实现重构所需的脉冲数量级在10-1至10-2m/s数量级，所需的总速度增量消耗约为0.76 m/s。对于比冲为3 km/s的轨控发动机，所耗燃料质量约为航天器总质量的0.025%，符合工程实际的合理范围。

表1 脉冲时刻与速度增量(Vx=0)

图2和图3分别给出了重构过程中的相对位置和相对速度轨迹，且图4给出了重构过程中的相对转移轨道。由图可见，从航天器从较小的编队构型出发，经过4次脉冲变轨后，进入较大的编队构型，从而实现了编队重构，证明了式(12)的正确性。

图2 相对位置轨迹(Vx=0)Fig.2 Time histories of relative position (Vx=0)

图3 相对速度轨迹(Vx=0)Fig.3 Time histories of relative velocity (Vx=0)

图4 重构转移轨道(Vx=0)Fig.4 Transfer trajectory of formation reconfiguration (Vx=0)

3.2 迹向欠驱动

选定的3次脉冲时刻见表2。对应地，由式(18)计算得到的脉冲速度增量也列于表2。可见，单次脉冲的速度增量消耗约为10-1m/s数量级，且总速度增量消耗约为0.83 m/s，在本算例中略多于径向欠驱动情况。同理，对于比冲为3 km/s的轨控发动机，所耗燃料质量约为航天器总质量的0.028%，符合工程实际的合理范围。

表2 脉冲时刻与速度增量(Vy=0)

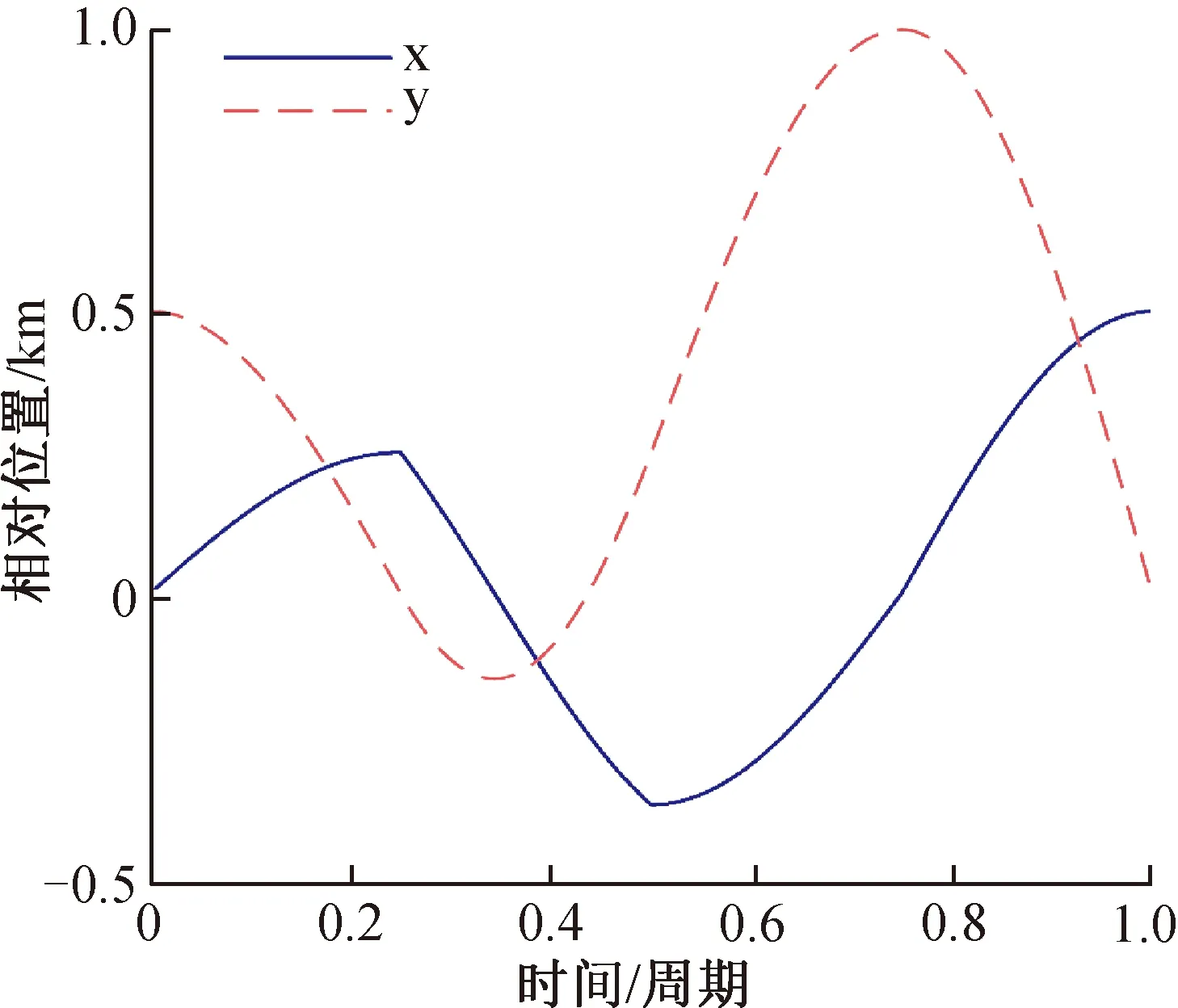
图5 相对位置轨迹(Vy=0)Fig.5 Time histories of relative position (Vy=0)

同理，图5和图6给出了迹向欠驱动条件下重构过程的相对位置和相对速度轨迹。图7给出了重构过程的相对转移轨道，可见，从航天器从较小的编队出发，经过3次变轨后，到达期望的编队，实现了编队重构，验证了式(18)的正确性。

图6 相对速度轨迹(Vy=0)Fig.6 Time histories of relative velocity (Vy=0)

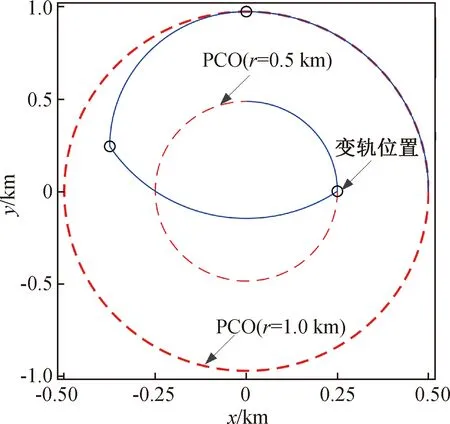
图7 重构转移轨道(Vy=0)Fig.7 Transfer trajectory of formation reconfiguration (Vy=0)

4 结束语

本文研究了径向和迹向欠驱动条件下的圆轨道编队重构脉冲控制问题。基于两类欠驱动条件下的相对轨道动力学模型，开展了系统能控性与重构可行性分析，并基此解析推导了实现重构所需的最少脉冲次数以及对应的脉冲速度增量。理论分析与仿真结果表明径向或迹向欠驱动条件下，圆轨道编队重构仍可行。通常条件下，径向欠驱动时，实现轨道面内重构所需的最少脉冲次数为4次；迹向欠驱动时，实现轨道面内重构所需的最少脉冲次数为3次。相较于全驱动重构控制方案，本文提出的欠驱动控制方案可有效避免由推力器故障引起的重构任务失效。此外，若主动采取欠驱动控制方案，可有效减少推力器数目，减轻系统质量，降低系统成本，满足编队航天器小型化、低成本的发展需求。当前研究针对二体圆轨道，后续研究将进一步考虑摄动因素以及椭圆参考轨道，进行欠驱动编队重构控制设计，并对脉冲时刻与脉冲速度增量进行优化。