基于BPPID控制的T型三电平逆变器中点电位平衡的研究
李家强 屠立忠 唐立 蔡海艳
摘 要:文章针对当T型三电平的平衡电路中两个桥臂的电容和电感元件不平衡时,如何采取控制策略抑制中点电压波动的问题。通过建立模型分析得到T型三电平中点电位不平衡的原因,增设平衡电路,采用两个LC串联桥臂的平衡电路控制中点电位平衡。在运行过程中,LC通常会受外部环境干扰,如强耦合,电磁扰动等因素使得平衡电路中点电位产生波动,因此文章提出一种基于BP神经网络的PID控制器(后文简称BPPID)。对BPPID控制器进行了Matlab/Simulink仿真研究与分析。仿真结果表明,基于BPPID控制的T型三电平逆变器具有操作可行性。
关键词:T型三电平;BPPID控制;中点电压平衡
中图分类号:TM464 文献标志码:A 文章编号:2095-2945(2019)24-0017-03
Abstract: This paper aims at the problem of how to adopt control strategy to suppress midpoint voltage fluctuation when the capacitance and inductance of two bridge arms in T-type three-level balance circuit are unbalanced. Through the establishment of the model, the reason for the imbalance of the midpoint potential of the T-type three-level is obtained, the balance circuit is added, and the balance circuit of two LC series bridge arms is used to control the balance of the midpoint potential. In the process of operation, LC is usually disturbed by the external environment, such as strong coupling, electromagnetic disturbance and other factors make the midpoint potential of the balance circuit fluctuate, so a PID controller based on BP neural network (BPPID for short) is proposed in this paper. The Matlab/Simulink simulation of BPPID controller is studied and analyzed. The simulation results show that the T-type three-level inverter based on BPPID control has operational feasibility.
Keywords: T-type three-level; BPPID control; midpoint voltage balance
T型中點钳位式三电平逆变器(“T” type neutral point clamped,T-NPC)单相拓扑结构图于2007年被学者KNAUP、Peter提出,T型三电平是近年该领域学者在三电平电路基础上改良优化的成果,在工程实践中已经展现出其不错的应用价值[1-9]。T-NPC和传统三电平电路的异同主要如下:T型三电平逆变器与传统三电平逆变器相同点在于主要都是用于三相交流电路的逆变过程,二者都包括调制模块、控制模块、滤波模块和含有IGBT的逆变电路模块;区别就在于逆变电路模块存在差异,T型三电平电路比传统三电平电路少了两个IGBT,这样降低了维护的成本,同时降低了控制的难度,开关寿命周期变相得到了延长。但逆变器中点电位波动的问题必须要解决,造成逆变器中点电位波动的原因有很多,在平衡电路环节,PWM调制环节,控制环节都会对中点电位波动产生影响。在脉宽调制时,非冗余矢量会造成中点电压偏移,因此有很多学者在SPWM和SVPWM基础之上进行和混合式的三电平控制策略[10],使得中点电位波动问题得到极大改善。
此外,有学者提出在三电平电路里增设平衡电路模块,这对于中性点电位的抑制具有很好的效果。相关平衡电路的拓扑结构有很多,本文的研究重点不在讨论平衡电路的选取,因此本文在建模仿真部分只选取了一种在原有并联电容上串联电感[4]的平衡电路。平衡电路参数调整会产生系统误差,采取什么样的控制策略对减少系统误差非常关键。传统的PID控制策略设计简单,易于实现,然而参数控制需要进行大量的计算,因此有学者在此基础之上嵌入了自适应调节模块[11],从而使系统调节更加智能化,中点波动后调节时间明显缩短。
但是,长期工作状态下,平衡电路中的电容电感受到外部干扰会发生变化。电容随着高温、高压和放电深度会发生老化,电感元件受到电磁干扰,耦合亦会发生变化,当平衡电路中的元器件自身大小发生变化后,对于中点电位也会产生波动。
为了解决这一问题,本文通过搭建平衡电路,通过BPPID控制策略实现跟踪当电容与电感值产生变化后,建立新的传递函数关系式,通过调节新传递函数PID参数减小中点电压波动。在matlab/simulink中分别对BPPID控制器进行建模分析,采用BP神经网络的PID控制器具有可行性。
1 T-NPC及中点电位不平衡因素分析
1.1 T-NPC
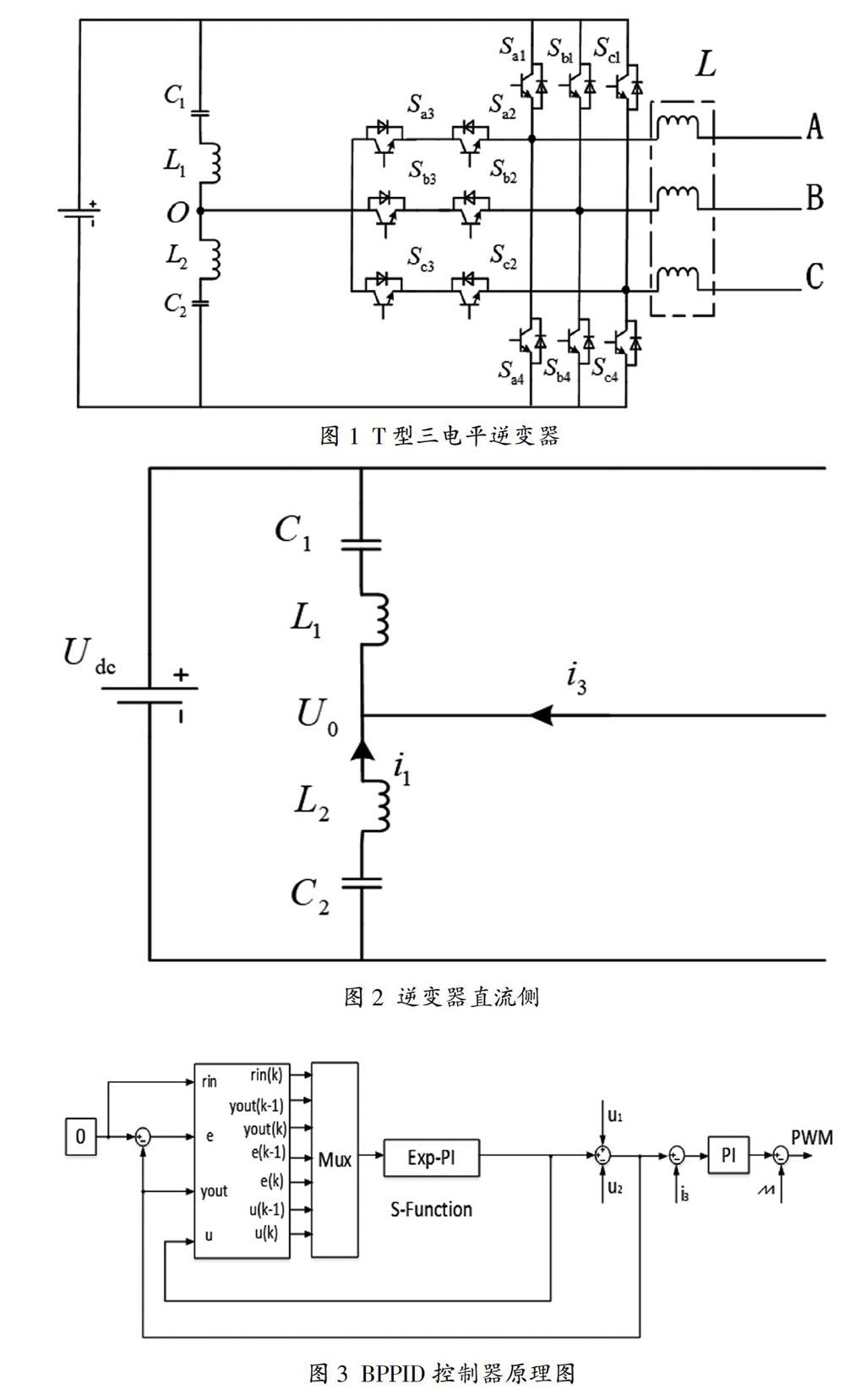
图1 所示为一种T型三电平的拓扑结构图,采取的平衡电路即图中两个桥臂上串联的电容和电感部分,其中C1和L1为平衡电路的上桥臂,C2和L2为平衡电路的下桥臂。O点即T型三电平的中点。
1.2 中点电位不平衡分析
T-NPC直流侧模块主要分为PWM调制模块,平衡电路模块和控制模块。因此造成中性点电位发生偏移的原因主要从以下几个模块去分析:(1)PWM模块中产生的,非冗余矢量会对电路结构造成中点电压偏移;(2)控制模塊中,当系统发生变化时,PID控制器的控制参数不能根据系统变化而进行实时跟踪反馈;(3)平衡电路模块中,当系统处于长期运行状态下,直流侧电源电压随时间变化不稳定并且容易波动,平衡电路中的电容电感受到外部干扰会发生变化。电容因为温度、电压和放电深度的影响会发生老化,电感元件受到电磁干扰,耦合亦会发生变化。本文重点讨论电感电容元件值发生变化时,结合图2进行具体分析。
如图2所示,左侧的Udc为传输端的直流电源,其中C1和L1为平衡电路的上桥臂,C2和L2为平衡电路的下桥臂。电流流入的正方向如图所示,对直流侧电路进行拉式变换后,再由KCL,可得电流i3输入与输出的开环传递函数:
(1)
可以通过仿真模型确定系统每一部分参数,从而通过PID调节器修改该传递函数的特性。
2 BP神经网络及基于BP神经网络的中点电位控制策略
2.1 BP神经网络
BP(back propagation)神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络。本文基于BP神经网络算法的T型三电平中点电位平衡控制方法具体步骤和特点如下:
步骤一:编写BP神经网络PI控制器核心部分S函数。
步骤二:将T型三电平并网逆变器、平衡电路、和BP神经网络PID控制器连接。
步骤三:将期望值、实际值、偏差作为输入,进行自学习后,输出PID的控制参数。
2.1.1 BP神经网络的S函数
因为BP神经网络PID控制器不是一个简单的输入输出关系函数,要经过三层处理得到其输入与输出关系,因此不能直接用传递函数来描述。S函数可以帮助建立起传递函数和BP神经网络之间的桥梁。本文借鉴了别的学者研究成果[12],编写了BP神经网络S
函数的代码,并将BP神经网络系统嵌入到T型三电平系统中。
2.1.2 BPPID控制器原理
图3为BPPID控制器的原理图,通过收集平衡电路两端电压信号,计算出实际电流值,再与预设的电流额定值进行比对得到开环传递函数,将该开环传递函数的信息输入到BP神经网络中进行自学习。
本文使用的BPPID控制器是三层BP网络结构,即3输入(IN)(即电流期望值,电流实际值和偏差值),隐含层数(H)为5,输出层数(OUT)为3(其中该层次对应比例系数Kp、积分系数Ki、微分系数Kd),T是采样周期,本文选用的采样周期为200ms。
2.2 中点电位控制策略
由于本文重点研究的是平衡电路元器件不平衡状态下的工作状态,在图1中IGBT关断时间,电感L1的能量全部转移到电容C1上,电感L2的能量全部转移到电容C2上,此处为了简化运算不妨在仿真模型中使两组电容和电感值乘积相等,经仿真验证,此方法可以有效验证平衡电路的稳定运行。
3 Matlab/Simulink仿真与分析
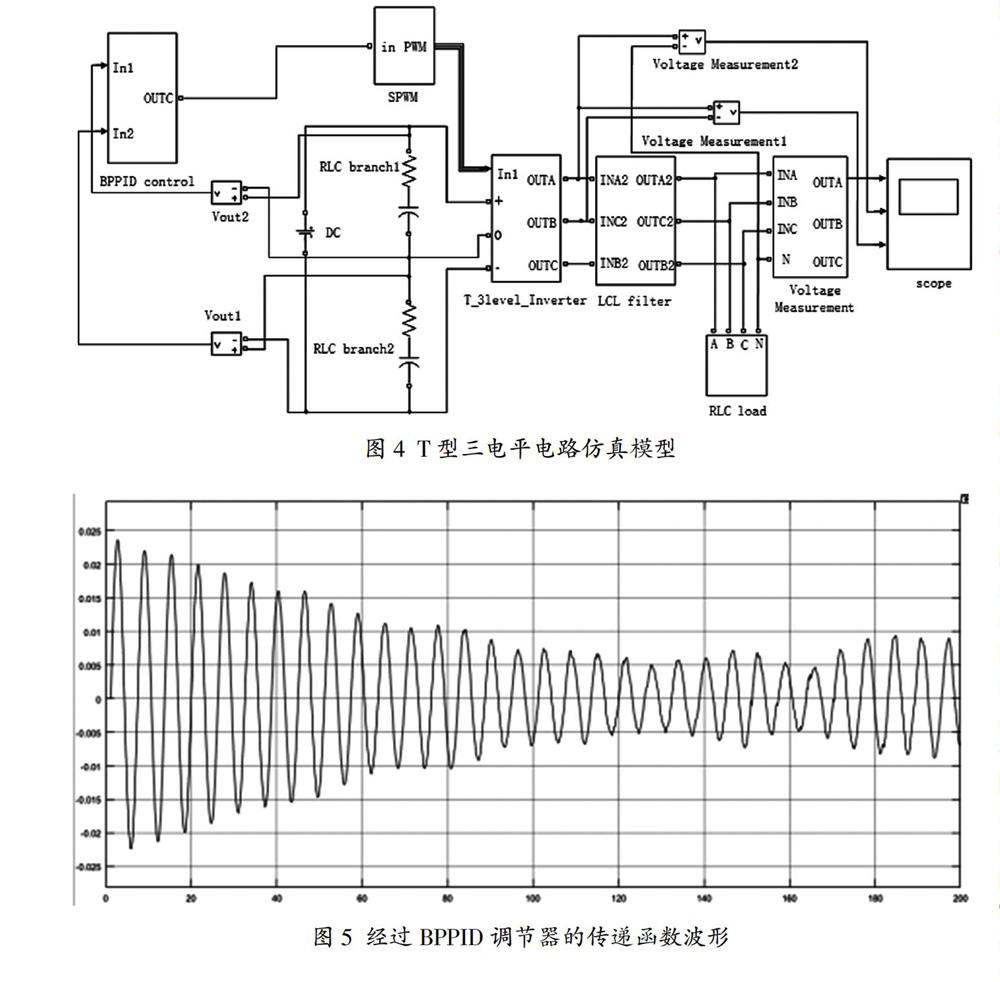
为了验证本文提出的在平衡电路出现不对称的情况下,BPPID控制策略对于T型三电平逆变器中性点电位是否具有正确性与实际可行性,在Matlab/Simulink平台中搭建了相应模块。图4为T型三电平电路仿真模型。
将系统采样周期设为200ms,可以得到图5的波形。
当时间在100ms之后,该传递函数误差会在±0.01dB之间波动,中点电位已经能够被控制在合理范围之内。
参考文献:
[1]毕长煜.基于时间补偿的三电平逆变器中点电位平衡控制[J].电气技术,2016,17(6):9-12,17.
[2]苏家庆.一种新的三电平光伏逆变器中点平衡算法[J].电气技术,2016,17(8):46-49.
[3]李龙,刘重阳,贲洪奇.基于神经元PI控制的PWM整流器动态特性研究[J].电力系统保护与控制,2013,41(11):124-128.
[4]潘胜和.NPC型三电平逆变器及其中点电压平衡的研究[D].武汉:华中科技大学,2014.
[5]单亮.基于TMS320F28335的T型三电平光伏并网逆变器的设计与实现[D].合肥:合肥工业大学,2017.
[6]王慧敏,温坤鹏,张云,等.基于精细分区控制的三电平逆变器中点电位平衡策略[J].电工技术学报,2015,30(19):144-152.
[7]龚博,程善美,秦忆.基于载波的三电平中点电压平衡控制策略[J].电工技术学报,2013,28(6):172-177.
[8]吴云,尹若银.三电平逆变器中点电位平衡电路仿真[J].煤矿机械,2014(5):57-58.
[9]李会南.基于T型三电平双模式逆变器的控制技术研究[D].北京:北京交通大学,2015.
[10]叶满园,韩祥鹏.T型三电平逆变器中点电压平衡控制[J].电力系统及其自动化学报,2018,30(09):16-21.
[11]李闯,黄陈蓉,徐宏健,等.基于神经元ProportionalIntegral自适应控制的T型三电平逆变器中点电位平衡控制研究[J].电气技术,2019,20(04):26-31.
[12]杨艺,虎恩典.基于S函数的BP神经网络PID控制器及Simulink仿真[J].电子设计工程,2014,22(04):29-31+35.

