求解大规模SCAD回归问题的随机坐标下降算法研究
赵 磊 陈 玎 朱道立,
(1.上海交通大学 安泰经济与管理学院,上海 200030;2.上海交通大学 中美物流研究院,上海 200030)
(1)
即求出各特征(因素)的回归系数构成的向量β=(β1,…,βp)T∈Rp,和截距项β0。最经典的回归系数向量(β0,β)的估计模型为最小二乘估计模型(least squares estimator,LSE):
(2)
随着大数据技术的发展,数据产生的源头逐渐增加,数据收集的难度逐渐降低,从而造成数据规模和复杂性逐渐增加。此外,数据的维度(属性)通常很大,可以达到成百上千维甚至更高(例如文档数据、基因表达数据、图片数据、多媒体数据、贸易交易数据等)。在对应的回归问题中,样本数据的维数p往往很大,样本量n往往远远小于p,即p≫n。以基因挖掘为例,通常是从成千上万维的核苷酸数据中挖掘出临床表现,但样本量往往很小。例如Scheetz et.al.(2006)的例子中,需要在120只12周大的小白鼠的18976条基因信息中进行挖掘,这一案例中p=18976,n=120。
在这种情况下,特征向量x_i的很多属性往往线性相关,传统的LSE方法通常很难处理这样的数据。因此,一些统计学家在经典LSE方法的基础上加入变量筛选功能,以适应高维数据的处理,即将LSE模型推广为如下带稀疏惩罚项的最小二乘形式:
(3)
其中,稀疏惩罚函数φλ(θ)可以有多种形式,常见的有岭回归(ridge regression)、套索回归(least absolute shrinkage and selection operator,LASSO)、平滑削边绝对偏离(smoothly clipped absolute deviation, SCAD)正则回归等。随着大数据时代的到来,这一类统计方法由于其在处理高维数据的优越,越来越受到数据科学家的重视,近几年在机器学习、统计学习、数据挖掘等领域被进一步研究。
岭回归中,φλ(θ)通常选取如下平方形式:
φλ(θ)=λ|θ|2
(4)
LASSO回归中,φλ(θ)通常选取如下绝对值形式:
φλ(θ)=λ|θ|
(5)
SCAD回归中,φλ(θ)通常选取如下分段函数形式:
(6)
其中,a>2,λ>0。如图1所示,二维空间中岭回归、LASSO和SCAD的惩罚函数分别为图中虚线、点划线、实线。

图1 二维空间中岭回归、LASSO和SCAD的惩罚函数图
前述三种带稀疏惩罚项的回归模型中,岭回归和LASSO回归模型在统计性质上是偏估计,SCAD回归是近似无偏的,因此SCAD回归具有更好的统计性质,能够被用来处理更加复杂的数据分析问题,例如存在奇异值的数据。但从回归模型的求解上来讲,LASSO回归、岭回归相应的最优化模型是凸的,可用一阶、二阶算法,随机坐标下降算法等进行求解(见Boyd),而SCAD回归是非凸的,造成了求解上的困难。但SCAD惩罚方法作为非凸惩罚项的前瞻性工作,直到现在仍受到理论和应用领域的广泛重视,因此有效求解SCAD的方法近年仍在被讨论。在大数据背景下,待求解的回归问题的数据量往往很大,数据源分布在不同的地理位置。这种情况使得进行大数据分析时,往往难以获得/处理完整数据。此外,由于数据规模大,算法的每一次迭代中更新全部变量会造成计算机的内存不足。因此,在大数据环境下求解SCAD回归问题时,往往难以实现在算法的每一次迭代更新全部变量。而现有求解SCAD回归的算法(LQA、LLA、ADMM等)在每一次迭代时均需要更新全部变量,这造成了现有求解SCAD回归的算法并不适用大数据背景下的应用。随机坐标下降方法(stochastic coordinate descent, SCD)以其每一次迭代中仅需要更新一部分变量的流程设计,减少了计算的内存需求,在大规模分布式最优化问题中得到了广泛的应用。但目前理论上SCD算法只能处理带凸惩罚项的回归问题,由于SCAD回归问题中的惩罚项是非凸和非光滑的,现有的随机坐标下降方法难以处理这一问题。
针对大数据时代高维数据、大规模数据、分布式存储的特点,本文研究大规模SCAD回归问题的随机坐标下降方法。为满足算法收敛的要求,我们分析得到SCAD回归模型的损失函数是导数Lipschitz、惩罚函数是semi-convex的分析结论。根据已有结论,得到SCAD回归问题的稳定点可保证良好的统计性质。在分析的基础上,我们设计了一种随机坐标下降方法(variable bregman stochastic coordinate descent, VBSCD),这一方法能在内存可控的前提下,很好地求解SCAD回归问题,且该方法任意收敛点均是SCAD回归模型的稳定点。此外,在该算法每一次迭代的子问题中,更新变量数量可根据需求自由选择,这一点很好地控制了算法每一次迭代中的内存需求。本文通过计算实验说明这一方法在求解SCAD回归问题时的有效性,决策人可根据随机坐标集合大小来控制子问题运算所需要的内存需求。
本文结构如下:第1节对SCAD回归问题的模型性质进行分析;第2节介绍求解非凸问题的随机坐标下降方法及其主要的理论结论,以及求解SCAD回归的随机坐标下降算法流程;第3节进行数值实验,说明本文方法的有效性;最后给出总结。
1 SCAD回归问题模型的性质分析
本节中考虑SCAD回归模型,即
(7)
其中,稀疏惩罚项φλ(θ)为如下形式:
(8)
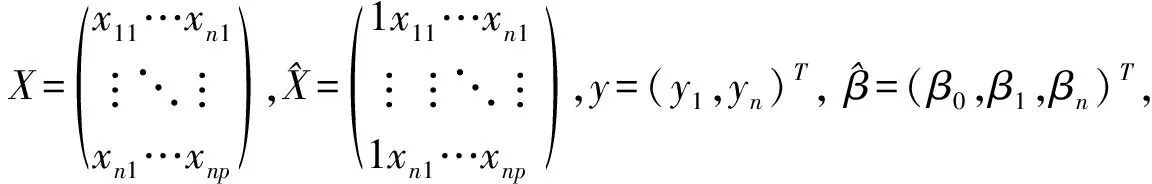
(9)
命题1:
‖▽f(x)-▽f(y)‖≤L‖x-y‖,∀x,y∈domf,
(2)惩罚项g(β)是semi-convex函数,即存在常数ρ≥0,
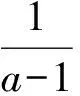
证明:
(1)根据定义有
(2)这里可直接对φλ(θ)进行分析,当θ>0时,φλ(θ)的次微分为
因此有
学习情境的设定是根据实际工作过程提出的,这要求教师有工程意识、过程意识及全局意识,要求教师具有行业从业经验。因此,制约地方新建本科院校向应用技术大学转型的瓶颈应该是具有行业背景的师资。
此外,根据[23]的结论,我们可知SCAD回归模型的任意稳定点与全局最优点具有基本一致的统计性质。通过上述分析,不难看出,算法可求得SCAD回归问题的稳定点,即可得到原始参数的较好估计。下一节中将应用本节中分析到的SCAD回归模型的损失函数是导数Lipschitz、惩罚函数是semi-convex的分析结论。
2 求解SCAD回归问题的随机坐标下降方法
2.1 求解非凸问题的随机坐标下降方法
最近Zhao和Zhu(2019)给出了求解如下非凸问题的随机坐标下降方法,针对的问题如下:
(8)

假设1:
(i)f是一个光滑函数,domf是凸的。f的梯度▽f是L-Lipschitz的;
(iii)F是水平有界的,即对任意r∈R,集合{x∈Rn|F(x)≤r}是有界的。
针对非凸问题(8)的随机坐标下降方法(variable bregman stochastic coordinate descent, VBSCD)流程如下:
选择初始解x0∈Rn
fork=0,1,…, do
从{1,…,N}中等概率选择i(k)
(9)
end for
在算法流程中D为Bregman函数,即D(x,y)=K(y)-[K(x)+〈▽K(x),y-x〉],在Bregman函数中,K为核函数,为步长参数。核函数K和步长参数服从假设2。
假设2:
(i)K是m-强凸函数,且其梯度▽K是M-Lipschitz的。
在非凸问题(8)满足假设1,算法VBSCD满足假设2的情况下,得到了如下结论:算法VBSCD产生的任意收敛点是函数的一个稳定点。
结合本节中算法性质和第二节命题1中SCAD回归模型性质,利用Zhao和Zhu最近提出的VBSCD算法可以求解SCAD回归问题。
2.2 求解SCAD回归问题的随机坐标下降算法

求解SCAD回归问题的随机坐标下降方法如下:
选择初始解x0∈Rn
fork=0,1,…, do

(10)
从{I1,…,IN}中等概率选择I(k),对任意j∈I(k),计算
(11)
end for
其中,子问题(11)有如下闭合表达式(见Fan和Li, 2001):
(12)
其中,rk=βjk+
通过上述算法流程,不难看出本文给出的VBSCD算法,在算法每一次更新中仅随机选择一部分变量进行更新,这一点很好地适应了大数据时代求解SCAD回归问题时数据规模大、分布在不同区域的需求。更新变量个数与所选择随机坐标集合I(k)的大小紧密相关。每一次迭代中,所需要的内存大小也和所选择随机坐标集合I(k)的大小紧密相关。下一节,我们将通过仿真实验,说明每一次迭代中选择随机坐标集合I(k)的大小与子问题求解内存需求、算法总迭代次数之间的关系。
3 数值实验
本节对两组仿真数据进行数值实验,通过数值实验说明:
(1)本文随机坐标下降算法可有效求解SCAD回归问题;
(2)本文随机坐标下降算法对不同规模算例求解时,所需迭代次数相对稳定;
(3)本文随机坐标下降算法在不同变量分组情况下,算法迭代到稳定点所需的迭代回合数(epoch)相对稳定;
(4)本文随机坐标下降算法随着变量分组的增加[随机坐标集合I(k)变小],每一次迭代中子问题计算内存需求减少。
3.1 数据集与计算环境
(1)仿真数据:样本因素数据X∈Rn×p的选择服从N(0,1)高斯分布,构造真实系数向量β*∈Rp,维数为p,稀疏度为s,β*中随机的s个元素为非0元素,其余元素为0。非0元素的值服从N(0,1)高斯分布。反应变量y=Xβ*+ε,其中各元素的噪声向量独立同分布,服从N(0,σ2),用σ来控制噪声大小。
根据上述规则,生成两组仿真实验,分别为σ=0.01、n=100、p=1000、s=10;以及σ=0.01、n=200、p=2000、s=10。
(2)计算环境:Intel Core i5-6200U CPUs (2.40GHz),8.00 GB RAM
3.2 实验结论
图2和图4中实线表示将变量分为100组时目标函数的下降情况,点线表示将变量分为50组时目标函数的下降情况,点划线表示将变量分为10组时目标函数的下降情况,虚线表示将变量分为5组时的目标函数下降情况。
图3和图5中圆圈(o)表示原始系数,星号(*)表示通过SCAD回归模型计算出的系数。
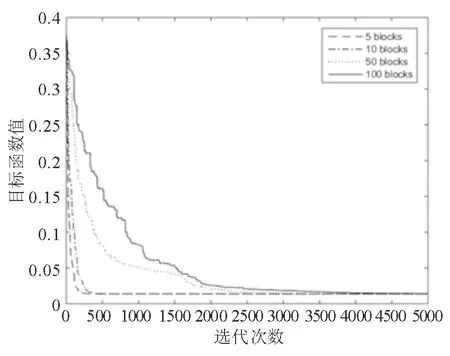
图2 n=100、p=1000、s=10时变量划分块数与算法下降效果之间的关系

图3 n=100、p=1000、s=10时信息恢复效果

图8表示对n=100、p=1000、s=10问题将变量分为1、2,5、10、50、100组时,求解子问题所需的内存大小。图9表示对n=200、p=2000、s=10问题将变量分为1、2、5、10、50、100组时,求解子问题所需的内存大小。
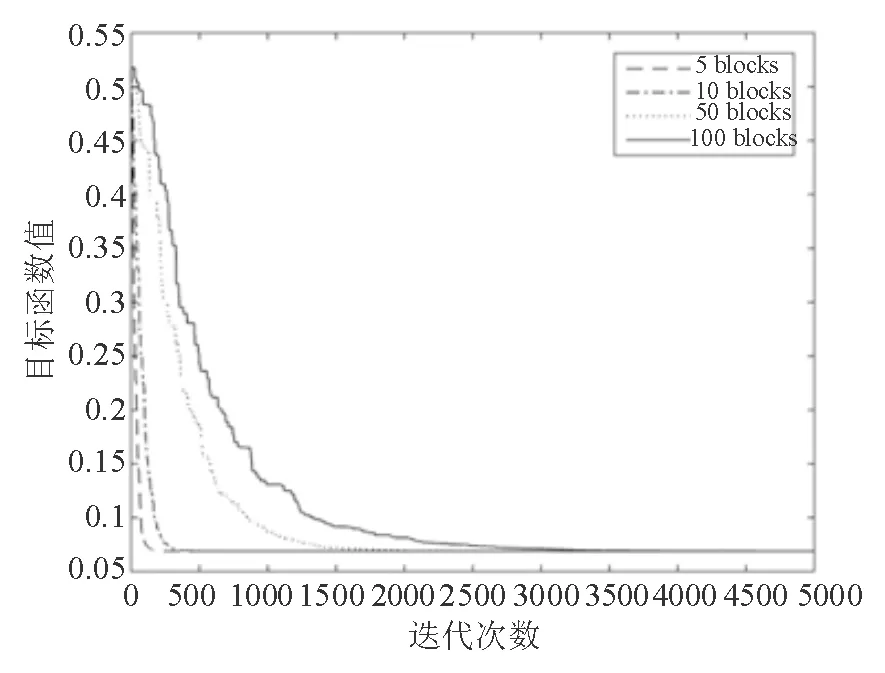
图4 n=200、p=2000、s=10时变量划分块数与算法下降效果之间的关系

图5 n=200、p=2000、s=10时信息恢复效果

图6 n=200、p=2000、s=10时变量划分块数、算法迭代回合(epoch)、目标函数下降效果之间的关系

图7 n=200、p=2000、s=10时变量划分块数、算法迭代回合(epoch)、目标函数下降效果之间的关系
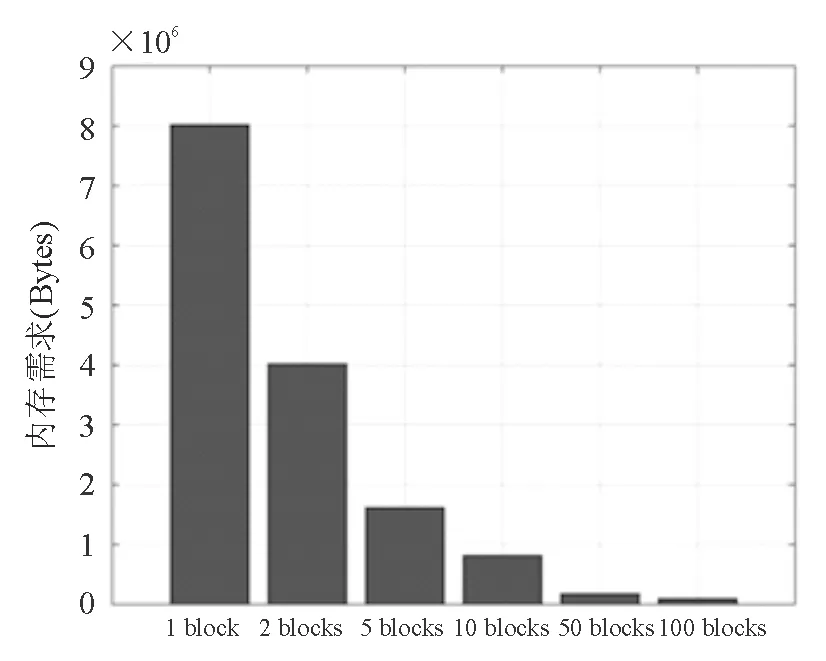
图8 n=100、p=1000、s=10算例,当把变量分成1、2、5、10、50、100组时子问题内存需求

图9 n=200、p=2000、s=10算例,当把变量分成1、2、5、10、50、100组时子问题内存需求
通过对图2至图9的分析有如下结论:
(1)本文随机坐标下降算法可有效求解SCAD回归问题:从图2和图4可以看出算法在迭代3000次左右时,即可收敛到较为稳定的解。从图3和图5可以看出SCAD回归具有很好的信息回归效果。图中圆圈(o)表示原始系数,星号(*)表示通过SCAD回归模型计算出的系数。
(2)本文随机坐标下降算法对不同算例规模所需迭代次数相对稳定:如图2和图4中,实线、点线、点划线、虚线的对比可以得到,随着拆分成的组(block)数量减少[随机坐标集合I(k)规模增加],算法收敛到所需要结果的迭代次数减少。此外,对比图2和图4,可以得到不同规模算例,在分组数一致的情况下,迭代到所需要点的所需迭代次数基本相同。
(3)本文随机坐标下降算法在不同变量分组情况下,算法迭代到稳定点所需的迭代回合数(epoch)相对稳定:如图6和图7所示,在两组算例中,目标函数值随迭代回合数增加而下降,其下降效率受变量分组数(随机坐标集合I(k)大小)影响不大。
(4)本文随机坐标下降算法随着变量分组的增加[随机坐标集合I(k)变小],每一次迭代中子问题计算内存需求减少:如图8和图9中可以得到,随着变量分组的增加[随机坐标集合I(k)变小],算法子问题所需计算内存减少。对比图8和图9,可以看出每组中变量的个数是子问题求解内存需求的关键因素,在每组选择变量个数相近的情况下,子问题的计算内存需求相近。
4 总结
SCAD回归问题,以其在处理高维数据中的近似无偏性,在大数据分析中得到广泛应用。但由于其惩罚项的非凸性,现有的随机坐标下降方法难以处理这一问题。本文首先对SCAD回归模型进行分析,得到SCAD回归模型的损失函数是导数Lipschitz,惩罚函数是semi-convex的,并根据已有结论得出SCAD回归模型的任意稳定点有良好的统计性质。基于这些分析,本文介绍一种新的随机坐标下降方法,可应用于求解大规模SCAD回归问题,算法的任意收敛点均是SCAD回归模型的稳定点。这一方法能很好地求解SCAD回归问题。本文通过计算实验说明这一方法在求解SCAD回归问题时的有效性,同时说明算法在不同变量分组情况下,算法迭代到稳定点所需的迭代回合数(epoch)相对稳定。随着变量分块数的增加,单次迭代中计算的内存需求减少。这一方法可被广泛应用于大数据分析和决策实践当中。
在大数据分析工作里,求解非凸非光滑的随机坐标下降算法的计算复杂度分析是个重要问题,Zhao和Zhu证明了在水平集次微分误差界条件下,随机坐标下降算法可以达到线性收敛,而Li和Pong证明了SCAD回归问题的目标函数满足该误差界条件。因文章篇幅问题,本文算法的计算复杂度分析不在此处做进一步讨论。

