区块链数据库:一种可查询且防篡改的数据库*

焦 通,申德荣,聂铁铮,寇 月,李晓华,于 戈

(东北大学 计算机科学与工程学院,辽宁 沈阳 110169)

通讯作者:申德荣,E-mail:shendr@mail.neu.edu.cn

随着比特币、以太币等一系列加密货币的兴起,其底层的区块链技术也受到了越来越广泛的关注[1,2].比特币最核心的意图是为了实现去中心化,即:在没有第三方信任机构参与的情况下,实现两个对等实体的数字货币交易.然而,现实世界中不可避免地存在很多自然中心,比如提供贷款的银行、提供电信服务的电信运营商等.虽然我们可以把这些中心机构当作对等实体,将其与用户的交易记录到区块链上,比如用比特币去交话费,但是这种做法是不切实际的,因为这不利于机构管理用户数据(包括用户的信用等级等).实际上,现有的中心机构都是由自己管理其存储用户相关信息的数据库,但是这种模式存在很多缺陷:(1)不同的数据库可能存储着相同的用户基本身份信息,导致数据冗余度高;(2)不同的中心机构各自管理自己的数据,不利于机构之间的数据共享;(3)每个数据库大都由单一机构中心化管理,使得用户必须无条件信任该机构,存在中心化问题;(4)用户不能够独立验证数据的正确性,如果数据被恶意篡改,用户与机构都无法察觉.不仅如此,在供应链以及商品溯源等领域,也对数据可信性以及数据可回溯提出了新的要求.

而区块链技术具有去中心化、防篡改以及可回溯的特性,为解决上述这些问题提供了可能.为此,我们提出了区块链数据库的概念,核心思想是:通过限制中心机构对数据记录的操作,来达到防篡改和去中心化的目的.该数据库中有多条区块链,每一条区块链相当于传统数据库中的一张表,所有的中心机构充当数据的存储节点,所有的存储节点根据共识算法生成区块链,所有节点(包括用户)存储区块头信息,可以由区块头信息检索到记录并验证记录的正确性.我们希望有高效的共识算法来提高系统的吞吐率,并有高效的查询算法实现在区块链上检索数据.当前,在共识算法上已经有很多研究,例如POW[3,4],POS[5,6],PBFT[7].然而针对区块链查询的研究相对较少,而且现有的区块链系统并不能兼顾数据回溯与数据查询.在比特币中可以根据每一笔交易回溯前一笔交易,但是存在的问题是交易本身不易检索.在以太坊中是状态树+交易树,状态树存储的是用户账号信息,状态树支持检索,可以根据状态树查询用户当前余额,但是状态树本身不记录历史信息,不能对状态进行数据回溯,而且状态树不直接关联交易,同样无法有效对交易进行回溯.虽然已有一些研究利用同步技术将交易数据同步到传统数据库,根据各数据项建立索引,从而实现快速查询,但是这种做法并不能保证索引的不可篡改,所以损失了区块链不可篡改的特性.基于此,本文提出一种不可篡改的索引结构,兼顾数据查询以及数据回溯.

本文首先提出了区块链数据库系统框架,将区块链技术应用于数据管理;其次,提出了一种基于哈希指针的不可篡改索引,根据该索引快速检索区块内数据,以此实现区块链的查询;最后,通过实验测试数据库的读写性能,实验结果表明,本文提出的不可篡改索引在保证不可篡改的同时具有较好的读写性能.

1 相关工作

文献[3]中,中本聪将数字签名技术、P2P 技术、时间戳技术、Merkle 树技术和工作量证明机制巧妙地结合起来,解决了双花与女巫攻击问题,实现了拥有去中心化、防篡改和数据可回溯等特性的数字货币系统——比特币系统.文献[8]中,Buterin 等人对比特币系统进行扩展,构建了新一代智能合约和去中心化应用平台——以太坊.除了比特币的功能之外,以太坊还有图灵完备的合约语言,内置的持久化状态存储,具有可编程性,使开发者可以很快地在以太坊平台上创建自己的区块链应用.这两个应用都是自下而上设计区块链,有内置代币,比特币主要应用于货币,而以太坊的主要功能则是智能合约.

文献[9]中,超级账本则采用自上而下的设计方式,去除了内置代币,提出了商用区块链框架.它采用了松耦合的设计,将共识机制、身份验证等组件模块化,使之在应用过程中可以方便地根据应用场景来选择相应的模块,除此之外还采用了容器技术,将智能合约放在docker 中运行,从而使得智能合约可以用几乎任意的高级语言来编写.

比特币、以太坊和超级账本三大应用平台的主要功能是针对数字货币与智能合约,但是数据管理性能较弱,一些机构发现了区块链不可篡改、去中心化与数据可回溯特性,力图将区块链技术与传统的数据库技术相结合,提升数据管理的性能,同时兼顾区块链去中心化、数据可回溯、防篡改的特性.

文献[10]中,Dinh 等人受区块链链式结构以及Git 版本控制的启发,为每个key创建设计了一个有向无环图,图中每一个节点对应key的某一历史版本,节点的前驱后继分别对应其版本的前驱后继,在保证高扩展性和高吞吐率的同时,实现了数据可共享与不可篡改的特性.文献[11]中,BigchainDB 将区块链技术与RethinkDB 相结合,在企业级分布式数据库的基础上添加区块链不可篡改和去中心化等特性,提出了一种基于管程的一致性策略,提高了数据的安全性,同时解决了区块链的数据存储容量问题.文献[12]提供了基于区块链的加密存储网络,通过将原始数据加密并签名后,保存到P2P 文件系统中,用户可以对数据的完整性进行验证.文献[13]中,Tuan 等人提出了一种区块链测试框架,包括针对区块链应用的一致性算法、数据模型、执行引擎和链上应用的测试方法,并且分析了以太坊、超级账本、Parity 以及UStore 的读写以及查询能力,对于区块链的设计以及瓶颈发现和解决带来了极大的帮助.文献[14]中,Tsai 等人总结了基于区块链的应用开发方法,给出了开发区块链应用时需要注意的关键问题,设计并实现了”北航链”.文献[15]中,Li 等人提出了一种高效的检索区块链的方法,包括范围查询和Top-k查询,有较好的灵活性.但是其解决方法是通过把区块链数据以及k-v数据库里面的数据同步到MongoDB 数据库中,利用MongoDB 进行查询操作,没有从根本上解决区块链的查询问题.为了将区块链技术应用于数据存储,ChainSQL[16]将数据库操作日志存储于区块链中,将数据存储于附属关系型数据库中,在底层支持SQLite3,MySQL,PostgreSQL 等关系数据库,可以根据区块链里的日志记录将数据库表恢复到任意时刻点,但是其恢复粒度是以表为单位,不利于以交易为单位的数据溯源.

2 区块链数据库系统框架

通过结合区块链和数据库技术,提出一种去中心化、防篡改同时支持查询的区块链数据库框架.如图1 所示,分4 层,具体如下.

· 存储层:在最底部,为k-v数据库,负责分布式存储数据,为每一个区块链备份多个副本;

· 网络层:是该框架的核心,负责节点间的数据传输以及根据共识协议确定区块的先后顺序.其中,节点由存储节点以及用户组成,每一机构为一个存储节点,用于存储本机构的数据信息,可以是一个数据库,也可以是多个数据库.当添加或者修改用户相关的数据时,需要由用户和机构共同签名认可;签名后的数据由机构封装到区块中,当区块大小达到某一阈值时,将其打包发送给其他机构进行验证.机构间根据共识算法验证区块的正确性,并决定区块的先后顺序.将验证正确的区块发送给存储节点存储,将区块头广播给所有节点,包括用户.在进行查询操作时,用户向存储节点发送查询请求,存储节点会返回查询到的记录项以及查询路径,用户根据查询路径以及区块头信息,可以验证查询结果的正确性;

· 区块链层:显示的是区块链的“世界状态”,上层应用可以据此对区块链数据进行查询操作;

· 应用层:是最上层,可以对查询到的数据进行进一步的分析处理.

针对这一框架,本文重新定义了数据库中的数据结构以及数据操作,并提出了Merkle RBTree 索引,基于哈希指针构建不可篡改的索引,在保证不可篡改的前提下实现高效查询.系统中数据的操作定义如下.

· 增加记录:数据在初次添加时,数据拥有者指定可以进行数据写操作的公钥,生成权限锁定脚本,然后用自己的私钥对该数据进行签名;

· 修改记录:操作者用自己的私钥对其父记录进行签名,然后验证该签名是否能够解锁父记录的锁定脚本,当且只当在解锁锁定脚本的情况下,才可以添加一条相同key值的记录,以此实现对父记录的修改.其中,权限锁定脚本只有数据拥有者可以修改.需要说明的是,数据修改与数据防篡改并不冲突,本文中的防篡改指的是对应版本的数据不可改且数据的更改历史不可改,但是支持数据从较老版本更新到新的版本;

· 查找记录:所有的参与者都可以进行查找操作,查找操作返回最新值为有效值,但是可以通过溯源操作查看该记录的完整修改历史;

· 删除记录:数据一旦添加便不可删除,当数据已经被修改多次,处于非常古老的版本时,为了节约磁盘空间,可以删除该数据的具体信息,但是该数据的哈希值则需要永久保存.

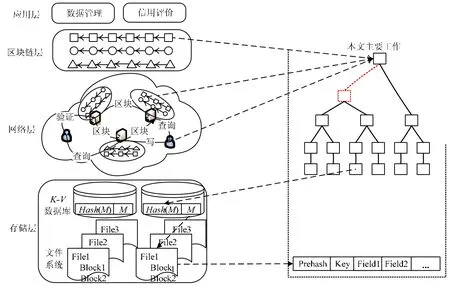
Fig.1 Blockchain database system framework图1 区块链数据库系统框架

3 区块链式数据模型

3.1 已有的区块链系统模型

(1)数据结构

为了能够较好地理解区块链的结构,我们给出了哈希指针的定义.一个数据项的哈希指针是指将该数据项的内容做哈希操作后得到固定长度的哈希值,同时以该哈希值为key,该数据项的内容为value,将此k-v对存储于k-v数据库,则该key即为该数据项的哈希指针.

区块链就是一个个的区块根据哈希指针首尾相连,每一个区块一旦形成便不可改变.如图2 所示,区块分为区块头和区块体两部分:区块头包括版本号、前一区块哈希指针(由前一区块头数据哈希得到)、区块形成时的时间戳、区块体中交易自下而上哈希得到的Merkle 根以及用于工作量证明的随机数和目标哈希;区块体中保存着区块中的所有交易记录.

如图3 所示,交易(transaction)包含版本号(nVersion)、交易输入(TxIn)、交易输出(Txout)以及交易时间(nLockTime).其中:交易输入包含其要花费的交易输出(preout)以及锁定脚本(ScriptSig),并且当且仅当SicriptSig是上一个输出中ScriptPubk 对应的私钥签名时才被认为是有效的;交易输出指定该笔交易的输出金额(nValue),以及收款人的公钥(ScripPubk).数字签名技术[17]保证每笔交易被支付到一个公钥里,然后只有拥有私钥的人才能花费掉这笔交易.

(2)数据读写流程

对于数据的存储管理,在写入数据时,每个区块的数据操作流程如下.

1)收集交易.将未写入到区块内的交易数据进行正确性检查(包括格式检查以及双花检查),并将有效的交易数据收集在集合(MapTransaction)中,其中,MapTransaction 只存放在内存中,其内存放了从交易哈希到交易的map 映射;

2)创建区块.将MapTransaction 中的数据添加到区块体中;之后运行PoW 机制,搜索合适的随机数值,使得区块头的哈希值小于目标哈希,从而证明该区块有效,即挖矿成功并获得奖励;

3)存储区块.在网络上将该区块广播,在本地将该区块顺序存储在本地磁盘文件(blk000x.bat)中;

4)更新区块索引(CblockIndex).在k-v数据库中更新CblockIndex,CblockIndex 记录着区块的磁盘存储位置以及该区块的前驱和后继区块,根据区块索引,能够得到区块链的世界状态;

5)更新交易索引(TxIndex).TxIndex 存储在k-v数据库中,包含每一笔交易的磁盘存储位置以及交易的后继交易(以该交易作为输入的交易).后继交易初始为空,标识该交易是未花费的,当该交易被花费后更新其后继交易,也是根据该标识位判断交易是否被双花;

6)将写入到磁盘的交易数据从MapTransaction 中移除.

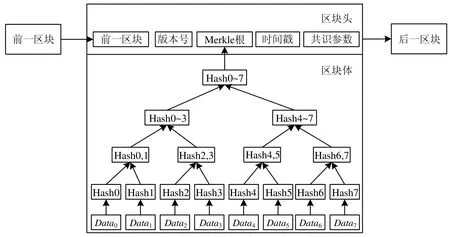
Fig.2 Block structure diagram图2 区块结构示意图

Fig.3 Transaction structure diagram图3 交易结构示意图

在读取数据的时候,必须要提供要读取数据的hash值,根据hash值,先在内存中的MapTransaction 中查找;如果没有查找到,则根据hash值到k-v数据库中查找对应索引信息TxIndex;最后,根据TxIndex 在磁盘文件blk000x.bat 中读取到数据.

(3)已有模型存在的不足

已有的模型利用数字签名技术以及MerkleRoot 来保证数据不可篡改和数据安全,但是其交易数据结构固定,只能处理固定结构的交易数据,不能处理一般数据,不适合传统数据库中的数据处理,缺少一般性;在进行数据读写操作时,只能够根据数据的hash值进行处理,在不知道数据hash值的情况下,无法进行数据查询操作.

3.2 面向数据库的区块链系统模型

针对已有模型中的不足,本文提出一种面向数据库的区块链系统模型,将交易结构扩展到任意记录格式,为每一个区块创建一个不可篡改的索引,在保证不可篡改的同时实现高效查询,为数据的所有者赋予新的语义,并重新定义数据操作.

(1)数据结构

为了能够操作更一般的数据,本文将交易结构进行了扩展,如图4 所示,交易分为交易头(transaction)和数据(data)两部分:交易头包含版本号(version)、父交易哈希(PreHash)、交易时间(nTime)、交易下一拥有者公钥(ScriptPubk)、证明本交易有效的签名(ScriptSig);数据部分类似于传统数据库中的表结构,包含关键字key以及各个字段(field).根据交易头部分实现数据的权限管理以及不可篡改和可回溯,根据数据部分记录各种类型的数据.其中,PreHash 指向相同Key 的前一交易.在进行写入数据的时候,首先查询是否存在关键字为key的交易:如果存在,则检验当前交易的SicriptSig 是否与前一交易的ScriptPubk 相匹配,只有在匹配的情况下,才认为交易有效;如果该key是第1 次出现,则将PreHash 置为0.在进行数据读取的时候,根据key进行检索,返回最近的查询结果,但是可以根据交易中的PreHash 进行溯源.数据的修改通过写入新交易实现,所有的记录都不可删除.

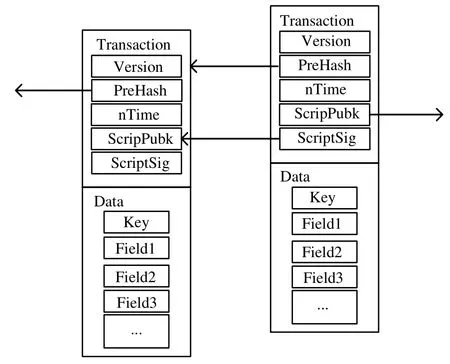
Fig.4 Database-oriented transaction structure图4 面向数据库的交易结构示意图

区块结构与已有的大体类似,特别之处是在区块的MerkleTree 中添加了关于交易key值的索引信息,使得可以从MerkleRoot 根据key值直接检索到对应交易,实现了交易的可查询性;同时,索引是经由Hash 运算保存在Merkle 树中,保证了索引的不可篡改.

(2)数据读写流程

为了实现针对于key的查询,写入数据时,在每一个区块中创建一个关于key的不可篡改索引,并将该索引记录保存在k-v数据库中;在读取数据时,根据key从区块头的MerkleRoot 开始索引,在O(logN)时间内索引到交易的hash值,然后根据该hash值到k-v数据库中查询到对应的TxIndex,最后,在磁盘文件blk000x.dat 中读取交易信息.

4 数据操作算法

4.1 Merkle RBTree索引构建

区块链数据库要求其数据满足不可篡改性,则对于数据的索引自然也应该是不可篡改的.我们定义区块一旦形成便不可修改,因此,我们对于每一个区块构造一个二叉查找树,然后将数据与二叉查找树一起做哈希运算,从而实现数据与索引的不可篡改.

我们选择红黑树和Merkle 树结合,选择红黑树有以下几个原因.

1)红黑树是二叉查找树,同时也是平衡二叉树,虽然不是完美平衡,但是能够保证查询复杂度为O(logN);

2)和Merkle 树一样,红黑树是由下往上生长的,从而能够保证父节点是由子节点哈希得到的,在插入新节点时,父节点信息可以得到相应更新.

然而,传统索引中的记录值并不是全部存储在叶子节点,其内部节点也都存储着记录值.然而这会在两个方面影响Merkle 树的性能.

1)不利于轻量级存在性证明.

如图5 所示:如果轻量级节点持有MerkleRoot 即H11以及记录信息Data4,我们想证明Data4是否存在于这棵树中.我们直接将序列{H3,H7,H9}发送给该节点,该节点计算Hash(Hash(H7,Hash(H3,Hash(Data4))),H9),如果得到的值等于H11,则证明Data4存在于这棵树中;否则不存在.其实,存在性证明就是通过将孩子节点两两哈希得到父亲节点,通过判断父亲节点是否相同来验证孩子节点的正确性.这就要求我们可以由孩子节点哈希得到父亲节点,但是如果父亲节点存放了与孩子节点无关的记录,我们便无法根据孩子节点哈希得到父亲节点,也便无法进行存在性证明;

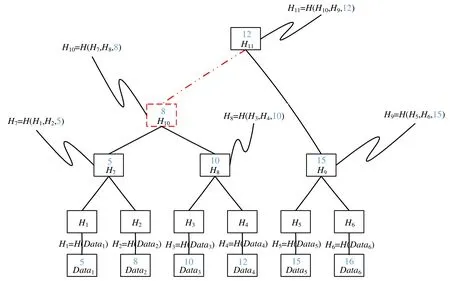
Fig.5 MerkleRBTree logical structure图5 MerkleRBTree 逻辑结构图

2)不利于分支删减,不能节省磁盘空间.

考虑到这样一种情景:Data1,Data2,Data3,Data4已经被修改过多次,而Data5,Data6则很少被修改,根据第2节对于修改记录的描述可知:前面4 个数据项已经有了很多后继,相当于非常久远的版本;而后两个数据项还是属于较新的版本.我们希望可以删除Data1～Data4但是不影响后续对于Data5,Data6的查询验证等操作.如果数据项都存在叶子节点,我们可以通过删除Data1～Data4只保留H10来节省磁盘空间而不影响树的功能;但是如果有数据记录存放在分支节点,我们便无法删除分支节点来节省磁盘空间,因为那样会影响树的功能(无法对剩余分支进行存在性证明).

因此,我们将索引内部节点的记录值往左下方移动,直到叶子节点为止,从而使得记录值只存放在叶子节点.在实现上,就是将小于等于节点关键字的记录存储在左子树,大于关键字的记录存放在右子树,中间节点只存放关键字和子节点hash值.

如图5 所示,共有6 条记录项:Data1,Data2,…,Data6,每个记录项都有一个关键值分别为5,8,10,12,15,16.按照关键值顺序将记录项存储到叶子节点中.分支节点中存放着左右子树的哈希值以及关键字,同时保证该节点的左子树中的关键值都小于等于该节点的关键值,右子树中的关键值都大于该节点关键值.

4.2 基于索引的数据操作算法

(1)数据插入算法

根据数据结构定义,节点结构如下.

叶子节点包含交易信息,中间分支节点存储索引信息.如果节点是分支节点,其lefthash和righthash分别为左右孩子节点哈希,key值等于左子树最大关键值.如果节点是叶子节点,其左右子树为空,为了区别于分支节点,其lefthash为0,righthash等于交易哈希值,value为交易记录.节点的哈希值定义为

我们从根节点开始插入数据,如果关键值小于等于根节点,则插入到其左子树;如果大于,则插入到右子树,直到最后一层分支节点h,根据如下所述4 种情况分别在该节点处插入新值.

· 情况1:如果该分支节点为空(只在MerkleRoot 为空时出现),先新建一个叶子节点存放(key,value)数据,然后新建一个分支节点,并定义其左孩子为叶子节点,关键值为key,左哈希为叶子节点哈希值.插入结果如图6(a)所示.这也说明了一棵树只要不为空,则其分支节点一定不为空,而且最后一层分支节点的key值一定与其左孩子key值相同;

· 情况2:如果待插入数据key值小于该节点key值,我们应该将该数据插入到该节点左侧,但是由情况1可知:该节点左孩子一定不为空,而且是叶子节点.为此,我们新建一个叶子节点存放待插入的(key,value)数据,然后新建一个分支节点,其关键字为待插入节点key,左孩子为新建的叶子节点,右孩子为原来分支节点的左孩子,父节点为原分支节点,插入结果如图6(b)所示,其中,连接和分支节点用虚线表示;

· 情况3:如果待插入数据key值大于该节点,而且该节点右孩子为空,则直接新建叶子节点存储数据,并将其定义为分支节点右孩子,插入结果如图6(c)所示;

· 情况4:如果待插入数据key值大于该节点,而且该节点右孩子不为空,我们先新建叶子节点存储数据,然后新建分支节点,分支节点关键值为待插入数据key值与原分支节点右孩子key值中的较小者,左孩子为待插入数据与原分支节点右孩子中key值较小者,右孩子为较大者,父节点为原分支节点,插入后结果如图6(d)所示.

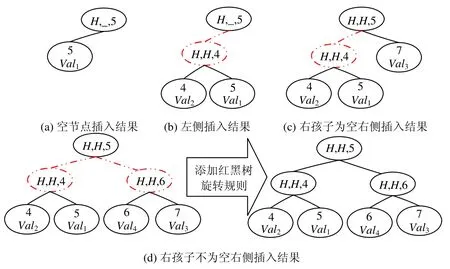
Fig.6 Example of last layer branch node insertion图6 最后一层分支节点插入示例

算法1.数据插入算法.

输入:根节点h,插入记录关键值key,插入数据值value;

输出:根节点.

· 算法1 的第2 行、第3 行是区块为空时的初始插入操作;

· 第4 行～第6 行是当插入key值小于节点key值时,如果该节点左孩子是最后一层分支节点,则按照之前所述情况2 插入数据;否则,以左孩子节点为当前节点递归插入数据;

· 第7 行～第10 行是当插入key值大于节点key值时:

➢ 如果右孩子为空,则该节点是最后一层分支节点,按照情况3 插入数据;

➢ 如果右孩子不为空,且是最后一层分支节点,则按照情况4 插入数据;否则,以右孩子为当前节点,递归插入数据;

· 第11 行～第13 行添加红黑树旋转规则,保证该树黑色平衡;

· 第14 行、第15 行更新节点哈希值.

数据插入之后,我们得到从根节点开始的二叉搜索树,而每个节点的哈希值即Hash(lefthash,righthash,key)又完全映射成一个基于哈希的不可篡改索引.数据是先写入到内存区块当中,当内存区块大小到达一定的阈值,则将该区块顺序写入到磁盘中,将其对应的MerkleRBIndex 存储到k-v数据库中.数据库中存储格式:

为了便于理解,可以认为MerkleRBIndex 对应一个map 集合mapMerkleIndex.

(2)数据查找算法

根据之前创建的索引,我们可以提供一种针对关键字key的查询方法,并且根据Merkle 树的特性,提供对应该查询结果的验证路径,使得轻量级客户端可以根据极少量信息去自我验证查询结果的正确性.

当输入关键值key时,首先在内存区块中检索,如果检索不到,就加载k-v数据库中上一区块的MerkleRBIndex 索引,直到检索到该数据项或者不存在该记录.当在特定区块中检索的时候,首先从MerkleRoot节点开始检索,如果目标关键字小于等于根节点关键字,则在mapMerkleIndex 中查找k为root.lefthash的目录,其对应的v则为下次要比对的对象;否则,查找root.righthash.最后,查询锁定在叶子节点,如果叶子节点的关键值等于目标关键值则查询成功;否则,记录不存在该区块中.

算法2.数据查找算法.

输入:关键值key,索引map〈Hash(lefthash,righthash,key),〈lefthash,righthash,key〉〉mmap;

输出:节点哈希值以及验证路径Vector〈〈hash,key〉〉path.

· 算法2 的第2 行初始化当前查找hash值为merkleroot;

· 第3 行～第9 行向下检索直到叶子节点,其中:第4 行～第6 行是如果目标key值小于等于当前索引项key值,则更新索引项为当前索引项的左哈希对应的索引项,并将其右哈希和索引key值保存在验证路径中;第7 行～第9 行对应目标key值大于当前索引key值的情况;

· 第10 行～第14 行是检验叶子节点是否包含目标key值:如果不在,则清空验证路径;如果在,则更新交易哈希值,并且将该项对应的验证值添加到验证路径中.

在图5 所示的MerkleRBTree 中,对于关键字key=10 的查询,从节点H11开始,依次查询H10,H8和H3,验证路径为path={(H9,12),(H7,8),(H4,10),(0,10)}.

本文提出的索引结构能够让索引自我检测索引的正确性和完整性.在区块内检索数据的过程,就是对mapMerkleIndex进行map 映射的过程.由于该map 最初是根据交易数据和索引信息自下往上两两哈希得到的,每一个条目都是确定且不可缺少的,当从最顶端开始向下检索的时候,能且只能检索到构建索引时存在的节点,直到叶子节点.如果在检索过程中指向一个map 中不存在的条目,则可以确定该索引数据缺失或者数据被篡改.

(3)数据验证算法

不仅存储节点可以在查询的时候检测到索引的正确性和完整性,而且用户节点可以在接收到查询结果之后对查询进行验证.如第2 节所述:用户节点存有区块头信息,而区块头当中有MerkleRoot 值,用户根据查询结果和验证路径,对路径上的值两两哈希生成查询结果对应的MerkleRoot 值,用户通过比较该值是否与自己保存的区块头中的MerkleRoot 值相同,从而验证查询的正确性.而且查询路径的长度对应交易在二叉查找树中的深度,对于含有N个交易的区块,任意交易的查询路径长度为logN,而且查询路径中的值为256 位的哈希值,验证的存储代价极小而且高效.

算法3.数据验证算法.

输入:交易信息tx,验证路径path,根哈希merkleroot;

输出:true or false.

算法3 的第2 行计算交易哈希值;第3 行～第5 行根据验证路径,从该交易开始向上重新生成父节点,最后生成根节点;第6 行～第8 行比对根据验证路径生成的根节点值与本地保存的根节点值,如果相同,则查询有效.

5 实 验

实验的硬件环境是Intel(R)Core(TM)i5-6500 CPU(3.2GHz),RAM 为8Gb 的PC 机,操作系统为Windows10.借助Bitcoin 的开源代码v0.1.0 版本构建了一个区块链数据库,实验中主要修改了Bitcoin 的底层数据结构,包括交易格式以及在区块中交易的组织形式,其中:交易格式扩展为支持更一般的数据格式,交易的组织形式由Merkle 树改为MerkleRBTree;保留了非对称加密技术以及UTXO 的思想,类比Bitcoin 中的公钥与私钥脚本结合形成价值传递轨迹,本实验中利用公钥私钥脚本结合形成数据的修改轨迹,并且利用该轨迹进行数据溯源.需要说明的是,本文的主要研究点是对于区块链数据的索引方法,不涉及网络以及共识协议,故在实验时利用单机进行测试,并将共识替换为检查交易的合法性,将有效交易存入到区块中,当区块大小达到阈值,则将整个区块存入磁盘.在本节中,我们设计多组实验来测试本文所提出的不可篡改索引的性能,实验中的主要指标为算法的运行时间,并将算法独立运行30 次的平均值定义为算法的运行时间.

· 实验1:MerkleRBTree 的性能测试

在比特币中生成区块时,需要对交易两两哈希得到 MerkleRoot.本文的模型中将 MerkleTree 替换成MerkleRBTree,在得到MerkleRoot 的同时生成对应的索引.我们设计实验测试了在区块交易数为26,27,…,216时对应的索引构建的时间代价.如图7 所示:MerkleTree 和MerkleRBTree 的构建代价随着交易数的增加而线性增加,有着相近的性能.说明在可接受的代价内实现了索引的构建,增加了查询功能.这里,MerkleRBTree 的时间代价多于MerkleTree 的时间代价,主要是因为在进行哈希操作时,MerkleTree 每次哈希输入为两个值,分别为左右子哈希;在MerkleRBTree 中,每次哈希操作为3 个值,分别为左右子哈希和对应的key值.

· 实验2:区块大小对于交易平均写入时间以及内存消耗的影响

交易到内存之后,需要等到形成一个完整区块才能存入到磁盘,这就使得第1 个进入到区块的交易和最后一个进入区块的交易有时间差,故在此取多个交易的平均时间.在这里,用交易数来度量区块大小,分别设置区块中最大交易数量为64,128,256,512,1024,2048,4096,8192,设置交易的字段数为3.如图8 所示,交易的平均写入时间随着区块最大交易数的增加而减小.这是因为区块中交易数越多,写入磁盘的时间代价均分到每一个交易上的代价就会越小.同时发现:当最大交易数为1024 以后,平均写入代价趋于稳定.另一方面,区块越大交易数越大,对应的内存消耗越大,且在区块交易数超过1024 以后,内存消耗增加明显.综合考虑两者因素,确定区块大小为1024 个交易.

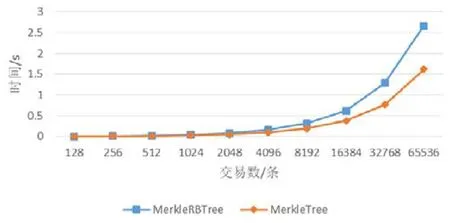
Fig.7 MerkleRBTree and MerkleTree build cost comparison图7 MerkleRBTree 和MerkleTree 构建代价对比

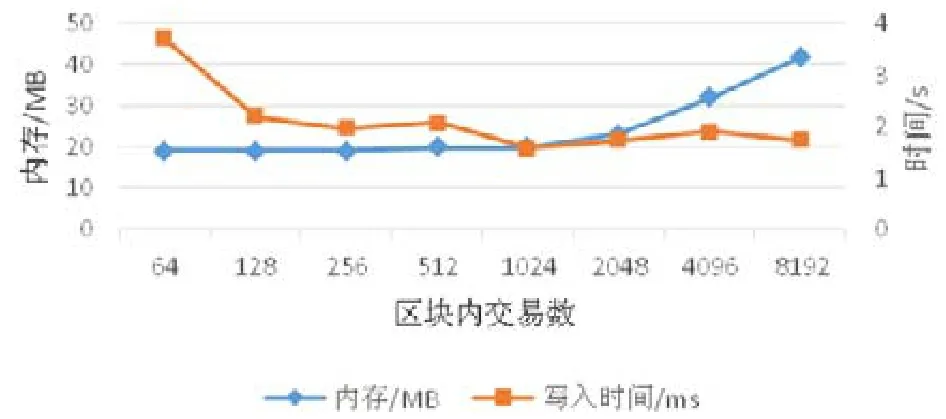
Fig.8 Impact of block size on memory and write time图8 区块大小对内存和写入时间的影响

· 实验3:key值查询与hash值查询性能对比

现有的区块链系统只能根据交易哈希值进行查询,哈希值形如“1ef4c1a9c62aa236766d2864c4c0f2d609aa83 d4f256dc35962a603a6832a476”抽象且与数据没有直接关联.本文实现了针对数据关键字key进行查询,我们设计的实验测试了针对key值与hash值的查询性能比较.如图9 所示,本文提出的针对key值的查询和比特币中针对哈希值的查询有相当的性能,表明在可接受的时间代价内,实现了交易的可查询性.

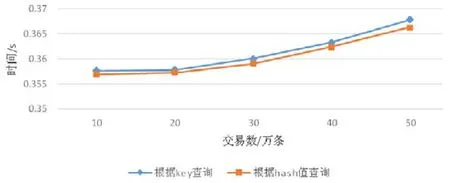
Fig.9 Comparison of key value query and hash value query图9 key 值查询与hash 值查询对比

· 实验4:区块深度对于查询时间的影响

数据在存储时是按照写入顺序依次添加到区块中,区块顺序写入磁盘.我们设计的实验测试了数据写入先后顺序对于查询的影响.实验中顺序写入50 万条key升序数据,每一个区块大小为1 000 条数据,一共500 区块,测试不同深度的数据查询时间.如图10 所示:数据查询操作并不受区块深度影响,对于先后写入的数据具有相近的查询时间,查询时间均匀分布在0.36s 左右.图中的异常点主要是因为在进行数据查询时,需要访问k-v数据库读取元数据信息,而k值为256 位的哈希值,k-v数据库的不稳定性导致了异常点的出现.

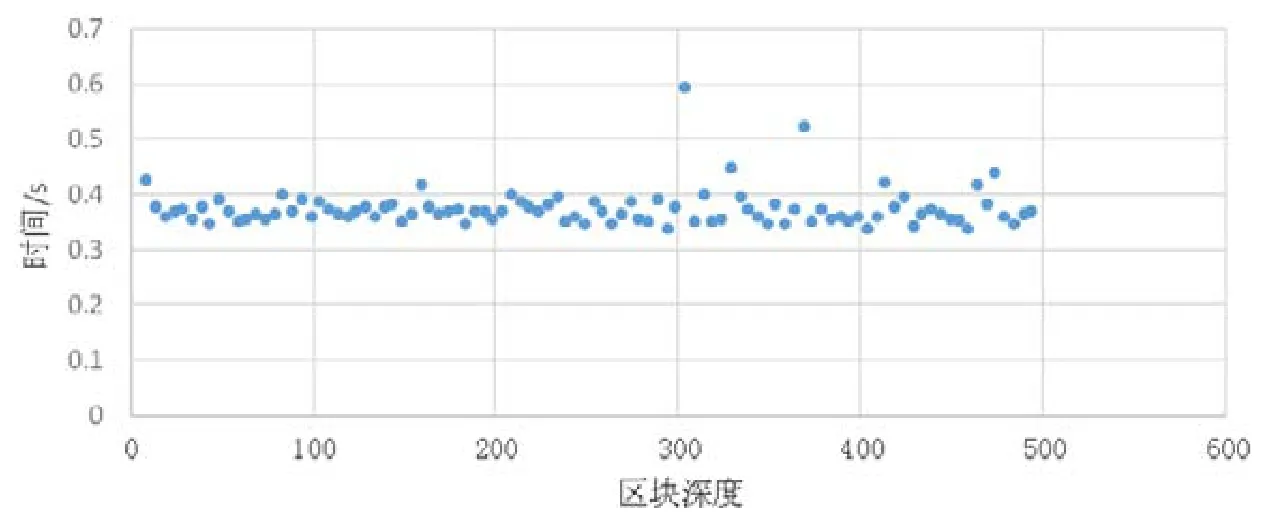
Fig.10 Block depth influence on query time图10 区块深度对于查询时间的影响

· 实验5:数据溯源性能测试

区块链的特性之一就是数据可回溯,即返回任意数据的完整修改历史.我们设计实验测试了数据版本数对于溯源时间的影响,分别设置7 条区块链,每条链的区块个数依次为10,20,30,40,50,60,70,区块中交易个数固定为1 024,交易的字段数固定为3,字段值为value+区块号,每个区块中key为0～1023,以此模拟数据的版本更新.分别在7 条链上针对同一关键字key进行数据溯源,记录查询到最初版本所需要的时间.如图11 所示,数据溯源的查询代价接近于单次数据查询的时间代价.这说明数据溯源的查询代价集中于最新版本的查询时间,历史数据的溯源时间相对于单次查询时间微乎其微,具有很好的溯源效率.

Fig.11 Impact of version number on query time图11 版本数对于查询时间的影响

6 总结

本文首先提出了一种区块链数据库模型,将区块链技术应用于数据管理;其次提出了一种基于哈希指针的树型索引结构,用于管理区块内的记录项,并由此实现查询;最后,通过实验测试数据库的读写性能.实验结果表明:本文提出的不可篡改索引在保证不可篡改的同时,具有较好的读写性能.同时,本文提出的针对key值的查询方法,是对于区块链数据库进行多值查询以及范围查询的基础,之后还会在此基础上进一步研究区块链的复杂查询.

当下人们对于数据安全的要求越来越高,区块链凭借着安全不可篡改的特性,必然会有出色的表现.然而要构建一个成熟的区块链数据库还需要一些后续工作.

(1)利用高效的共识算法提升系统的吞吐率;

(2)利用智能合约管理每一个数据项的读写权限,保证只有拥有者授权的公钥可以访问和修改数据.