基于威布尔分布的加速试验剖面设计方法

王海东,蒋 刚,陈志伟,贾 斐

(1.上海航天精密机械研究所,上海 201600;2.西安电子科技大学 机电工程学院,陕西 西安 710071)

0 引言

产品寿命是评价航空航天装备使用性能的重要指标。为准确、快速地评价航空航天产品的使用寿命,目前通常采用加速寿命试验方法进行产品定寿。加速寿命试验(ALT)是在合理的工程及统计假设的基础上,采用提高工作应力或环境应力的方法来使产品快速地暴露故障,再利用加速应力下的试验信息(失效数据、失效原因等)来外推产品在正常应力水平下的可靠性指标的一种寿命试验方法[1]。加速寿命试验采用加速应力进行试件的寿命试验,缩短了试验时间,提高了试验效率,降低了试验成本,其研究使高可靠长寿命产品的可靠性评定成为可能[2]。加速寿命试验受到国内外可靠性工作人员和工程研究人员的高度重视,且已被广泛应用于机电产品、半导体材料、武器装备及航空航天等实际问题中[3-7]。

加速寿命试验的类型很多,按照应力施加方式的不同,一般分为恒定应力加速寿命试验、步进应力加速寿命试验、序进应力加速寿命试验3种基本类型[8]。在NELSON[9]提出的累积损伤模型基础上,我国学者研究了不同分布类型下步进加速试验数据处理方法。序进加速试验数据处理方法难度较大,当前取得的研究成果相对较少,还未能成熟运用。恒定加速试验和步进加速试验应用较广泛,但步进加速试验对试验时间和样品数量需求更低,试验效率较高,已成为产品定寿试验的应用趋势。而二参数威布尔分布作为一种连续分布,可以很好地拟合各种类型的试验数据,因此被广泛应用于各个领域,特别是可靠性领域中的寿命数据分析,因此基于二参数威布尔分布的研究一直是可靠性领域研究的热点之一。镁合金是实际应用中最轻的金属结构材料,在航天航空产品领域具有广阔的应用前景[10-11],所制造出的产品也具有更高的可靠性,同样符合二参数威布尔分布。

1 试验剖面优化设计

1.1 设计变量

1.1.1 确定试验剖面

为了便于分析,将对简单三步进加速寿命试验剖面进行研究。三步进加速寿命试验剖面如图1所示。图中：粗黑线表示试验载荷施加方式;Tm为不改变失效机理的最大温度应力,可根据少量摸底试验或仿真确定;tc为试验截尾时间,可根据工程经验或者少量摸底试验确定;T1和T2为加速温度应力;t1,t2为应力转换时间。除此之外,产品正常工作温度应力为T0。

图1 三步进加速寿命试验剖面Fig.1 Three-step accelerated life test profile

1.1.2 模型归一化

由于参数较多,不便于分析。为了简便计算,且使各参数的取值与优化模型结果之间的关系模型更具一般性,需对模型进行标准化处理。

1)应力水平标准化

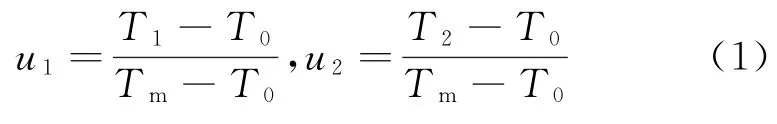
已知正常工作应力水平为T0,最高加速应力水平为Tm,令则加速应力水平T1和T2转化为标准应力水平u1和u2。

2)应力转换时间标准化

已知试验截尾时间tc,令

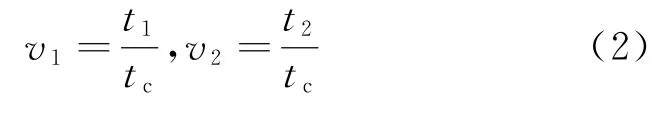
则应力转换时间t1和t2转化为标准应力转换时间v1和v2。

1.2 约束条件

针对三步进加速试验的设计变量有4个,分别为加速应力水平u1和u2,以及应力转换时间v1和v2。对应的约束条件有

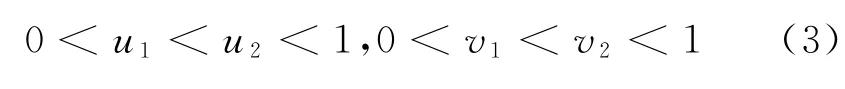
1.3 目标函数

1.3.1 确定分布函数

产品在不同应力水平下的寿命服从同一分布函数,且试验中所有随机试样都具有统计独立性。在常见产品寿命模型中,主要有指数分布、正态分布和威布尔分布,其中威布尔分布模型的应用较为广泛,因为威布尔分布模型具有多变的函数形态,能够很好地拟合各类数据。威布尔分布作为一种连续的概率分布模型,有近半个世纪的应用和研究历史,在机械可靠性工程中得到了一定的应用,二参数和三参数分布形式是威布尔分布的基本形式。常用的二参数威布尔分布的累积失效分布函数和概率密度函数分别为

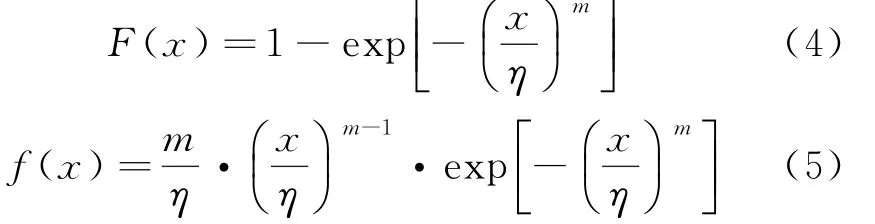
式中：x为失效时间;η为尺度参数,η＞0;m为形状参数(根据工程经验,0.5≤m≤5)。

为了使产品在不同应力水平下的失效机理保持一致,需假定产品在不同应力水平下分布函数的形状参数保持不变,即二参数威布尔分布的形状参数m保持不变。

1.3.2 确定加速模型

加速寿命试验的实质：当产品寿命特征处于高应力水平下时去外推产品处于正常应力水平下的寿命特征,其推导关键在于建立寿命特征与应力水平之间的数学关系,这种关系被称为加速模型或加速方程。常用的单应力加速模型有Arrhenius模型、逆幂律模型、Eyring模型和广义Eyring模型。本文考虑的加速应力只有温度,故采用Arrhenius加速模型,即

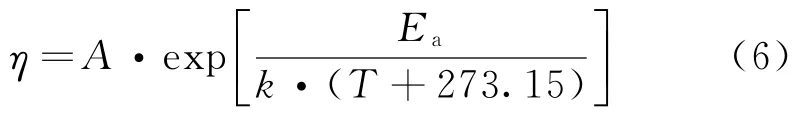
式中：T为环境温度,℃;Ea为激活能,e V;k为玻尔兹曼常数,值为8.617×10-5e V/K;A为未知常数。

将式(6)两边分别取对数,有

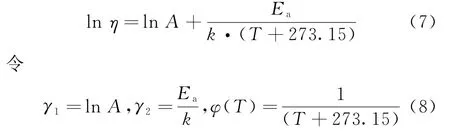
可将式(7)转换成对数线性关系式,即

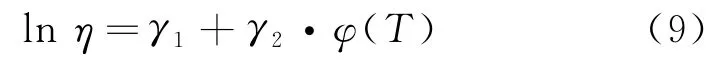
式中：γ1,γ2为未知常数;φ(T)为跟温度应力有关的函数。

1.3.3 构建累积失效模型

NELSON累积失效理论(CE模型),假设产品的剩余寿命仅依赖于当时已累积失效的部分和当时的应力水平,与累积方式无关。这一假定是NELSON根据物理原理提出的。如果产品的寿命分布为F(t),则该假定的数学含义是：某产品在应力水平Si下的工作时间为t i,则t i内产品的累积失效概率为F i(t i),相当于在应力水平Sj下工作时间为tj时产品的累积失效概率F j(t j),即F i(t i)=F j(t j)。根据这一假定,可对不同应力水平下的寿命数据进行折算。

根据NELSON 累积失效理论,由F1(t1)=F2(τ1),得

同理,由F2(t2-t1+τ1)=F3(τ2)得

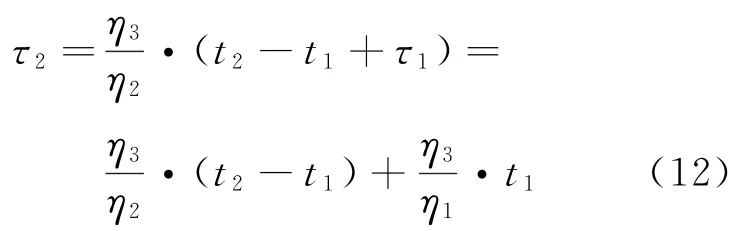
式中：τ1为在温度应力水平T1下试验t1时间换算到温度应力水平T2下的累积等效试验时间;τ2为在温度应力水平T2下试验(t2-t1+τ1)时间换算到温度应力水平Tm下的累积等效试验时间。

因此,试件失效时间X的累积分布函数为

对应的概率密度度函数为

式中：F1(x),F2(x),F3(x)分别为在温度应力水平T1,T2,Tm下的分布函数;f1(x),f2(x),f3(x)分别表示在温度应力水平T1,T2,Tm下的概率密度函数;η1,η2,η3分别为在温度应力水平T1,T2,Tm下的尺度参数。同时满足

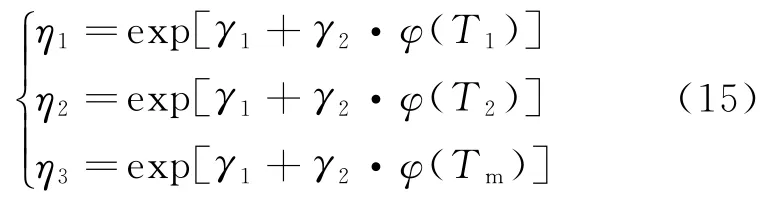
1.3.4 模型参数估计

由于加速试验普遍存在试验截尾、失效模式不确定等问题,因此突发型失效模式数据通常是非完整数据。极大似然估计(MLE)不仅适用于完整数据,同时适用于非完整数据,因此,选择MLE 对加速试验突发型失效模式数据进行统计分析。

假设第i个样本在时间xi失效,定义3个指示函数

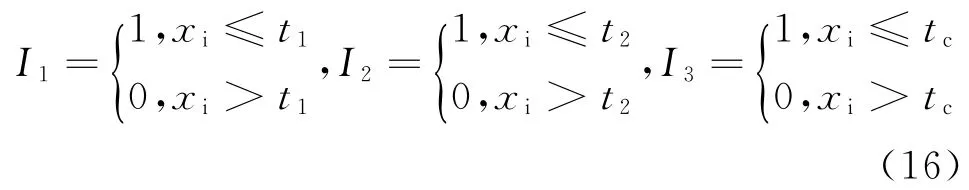
则第i个样本的对数似然函数L i为

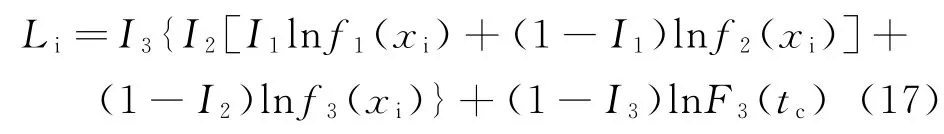
当投入试验的样本量为n时,则所有样本的的对数似然函数L为

解L的一阶偏导数方程组,由

1.3.5 分位数寿命估计

根据加速模型公式,可以计算得到在正常温度应力水平T0下的尺度参数η0的估计值为

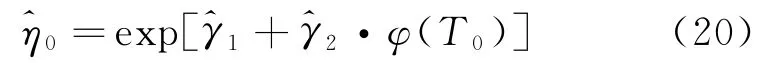
从而得到在正常温度应力水平T0下的累积分布函数为

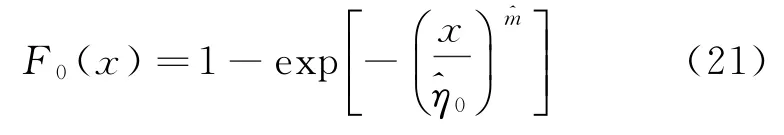
故产品的P阶分位数寿命x P的MLE估计值为

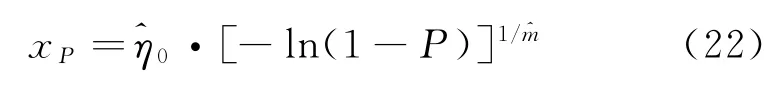
1.3.6 优化准则与渐进方差

1)优化准则

对于具有可靠性高且寿命长的产品,做加速寿命试验时,通常选取产品在正常应力下P阶分位寿命MLE估计值的渐进方差作为其可靠性寿命特征量。为提高该特征量估计精度,并减少试样数量、缩短试验时间,需要优化加速寿命试验方案。在正常应力下,以产品P阶分位寿命MLE 估计值的渐进方差最小为准则,对加速寿命试验方案进行优化。

2)寿命的渐进方差

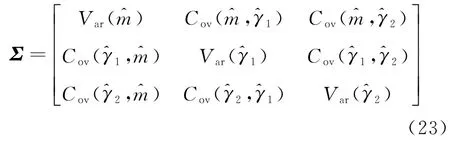
一般协方差矩阵难以求得,根据MLE 估计理论,协方差矩阵Σ与信息矩阵F为互逆,即Σ=F-1,故通常采取对信息矩阵求逆来求得协方差矩阵。而信息矩阵可由n个样本的对数似然函数对各模型参数的负二阶偏导数矩阵的数学期望求得,有

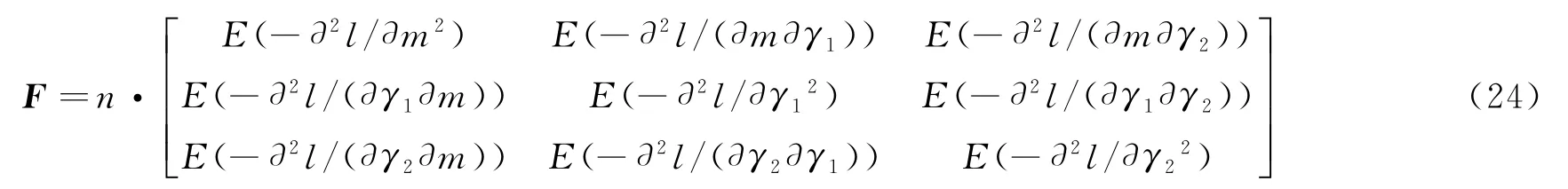
通常,极大似然估计量具有渐进无偏性和渐进正态性,故可得到在正常温度应力水平T0下,产品P阶分位数的对数寿命的渐进方差为

地铁供电系统中刚性接触网常见故障和防范措施解析……………………………………………………… 钟人正（7-72）

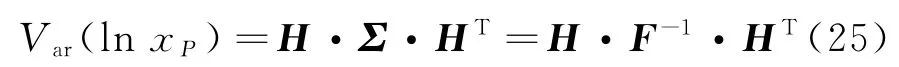
式中：H为一阶偏导矩阵,即

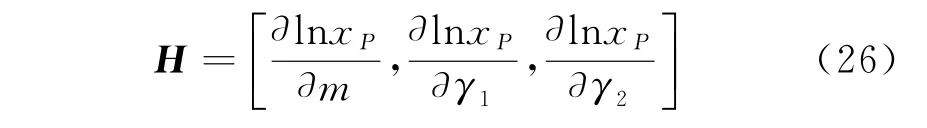
由式(1),(2)得

再将式(27)代入式(25)中,可得到只与4个设计变量u1,u2,v1,v2有关的渐进方差表达式。

经过推导计算,信息矩阵F里面的元素过于复杂,无法求出具体的定积分表达式,故采用数值积分的方法进行近似求解。考虑到使用数值积分需要已知积分区间,且整个推导过程中涉及到诸多变量替换,同时存在约束条件,故考虑使用非线性规划算法进行优化求解。而经典非线性规划算法大多采用梯度下降的方法求解,需知道显式的函数表达式,显然不适用,故综合考虑下决定使用随机Monte-Carlo模拟的方法进行优化求解,求使渐进方差取得最小值所对应的优化变量

2 仿真算例

结合部分工程经验,假设参数真值为m=2,γ1=10,γ2=2 300;温度应力水平分别为T0=20 ℃,T1=50 ℃,T2=80 ℃,Tm=110 ℃;试 验 时间为t1=40 min,t2=80 min和tc=120 min;试验样本量为n=40。

现以产品在正常温度应力水平T0下的对数中位数寿命估计值的渐进方差为优化准则,以加速应力水平u1,u2和应力转换时间v1,v2为设计变量,进行三步进加速试验方案的优化设计。

采用Monte-Carlo模拟的方法进行1 000次随机寻优求解的结果为=0.33,=0.82,此时所对应的渐进方差最小值为0.11。若采用传统均匀设计的加速试验方案：=1/3,,此时所求得的渐进方差为0.34。

显然,经过优化后的寿命估计值的渐进方差比传统均匀设计的渐进方差要小,这表明经过优化的加速试验方案比传统均匀设计的试验方案具有更高的估计精度。

3 结束语

为实现对高可靠性、长寿命产品在正常环境应力水平下寿命与可靠性的快速评估,本文在单应力情形下,研究了二参数威布尔分布的三步进加速试验的优化设计理论与试验数据的统计分析方法。通过建立Arrhenius与二参数威布尔分布试验的可靠性统计模型,以产品在正常温度应力水平下中位寿命估计的渐近方差最小为优化准则,给出了二参数威布尔分布的三步进加速试验应力水平与应力转换时间的优化设计方法,并通过与传统均匀设计加速试验方案的对比,表明经优化后的加速试验方案具有更高的估计精度。采用随机Monte-Carlo模拟的方法代替传统非线性规划算法进行加速试验方案设计变量的优化求解,以解决函数表达式过于冗长、计算复杂等问题。今后将考虑基于二参数威布尔分布进行多应力(如温度、湿度、振动等)综合加载方式下的步进加速试验统计分析与试验设计优化方法研究,并考虑基于二参数威布尔分布进行多步进(即加速应力水平数大于3)情况下的步进加速试验统计分析与试验设计优化方法研究。