基于远程监控数据的电动客车续驶里程估算方法
卢 凯, 赵云雪, 王 力, 刘洪民, 孙国伟
(1.中通客车控股股份有限公司,山东 聊城 252000;2.聊城市技师学院,山东 聊城 252000)
纯电动汽车在快速发展的同时也存在许多问题,最重要的是充电设备不配套、续驶里程短等。这两大问题严重阻碍了纯电动汽车的推广和发展[1]。因此本文探索根据电动汽车远程监控部分数据估算纯电动客车续驶里程的方法,为纯电动客车的使用提供比较可靠的参考信息。
1 续驶里程与各参数的相关性分析
本文的续驶里程[2-3]指的是:SOC为100%时,电动汽车开始连续行驶,当SOC降到某一值时所行驶的里程,可用以下公式表示:
续驶里程=(1-SOC某值)/每公里的SOC消耗量
经过试验验证,荷电状态低于10%时电池的性能极不稳定,很容易对电池物理性能造成不可逆的伤害[4-5];高于15%时,电池性能比较稳定。所以本文在估算续驶里程时,剩余荷电状态以30%为计。
1.1 续驶里程的主要影响因素
影响续驶里程的因素比较多且较复杂[6-7],主要包括电池性能(电池放电电压、电池单体电压、电池内阻等)、环境因素以及整车参数等。
1) 电池参数。电池参数和放电深度的关系比较复杂,但电池的电压、SOC等主要参数与放电深度呈线性关系[8]。在一定范围内,续驶里程与电池放电深度之间呈线性关系,而通过电池SOC可以估计出电池放电深度。所以电池参数间接影响车辆的续驶里程。
2) 环境温度。纯电动汽车的续驶里程受环境温度影响很大,主要影响电池内部的化学反应、电动汽车润滑油的粘度及能量消耗率。尤其在低温环境中电池消耗的能量大,并且充电容量和放电容量较常温环境都明显减少[9]。
3) 整车参数。电动汽车的整备质量、各附件功率消耗、行驶车速等参数都影响着电动汽车的续驶里程。当附件功率消耗较少,例如空调关闭状态、电动汽车整备质量较小以及低速行驶状态,都可以提高电动汽车的续驶里程。当电动汽车高速运行并且附件为打开状态时,续驶里程明显减少。
4) 其他影响因素。不同的驾驶习惯以及不同的载重量对续驶里程有很大影响[10-12];道路拥堵或者畅通直接影响着车辆速度,进而对续驶里程产生影响;当天气不同时,空气阻力和路面阻力会有所不同,也对续驶里程产生影响。
考虑到实际工况下影响电动汽车续驶里程的因素很多,本文选择相同路线的纯电动城市客车,以远程监控终端采集的相关数据为基础,选择电池的性能参数(SOC、电压、电流、温度)和车辆状态参数(车速)进行研究,以达到预测续驶里程的目的。
1.2 影响因素线性相关性分析
相关分析是研究随机变量之间是否存在某种依存关系的一种统计方法,可分为线性相关分析、偏相关分析、距离分析。本文采用数据为定距型,并以相关系数的数值大小反映变量间相关性的强弱。所以本文采用简单线性相关分析对变量进行相关性分析。
为了精确描述续驶里程和各个影响因素之间的相关性,并判断相关性的强弱,下面对菏泽市某路电动城市客车在2018年7月1日7:10至16:59、7月16日8:44至16: 48以及7月24日7: 43至17:32的放电数据进行相关分析,获得相关系数以及对应的显著性概率P值,具体分析结果见表1。

表1 各变量与续驶里程的相关性检验结果
由表1可知,续驶里程与 SOC、单体温度最低值、单体温度最高值的相关系数绝对值均大于0.8,且它们对应的显著性概率P值都近似为0,认为续驶里程与 SOC、单体温度最高值、单体温度最低值均具有强线性相关性。
续驶里程与总电压、单体电压最高值、单体电压最低值的相关系数绝对值均大于0.2且小于0.8,因此认为续驶里程与总电压、单体电压最高值、单体电压最低值具有弱线性相关性。
续驶里程与车速、总电流的相关系数绝对值均小于0.2,因此认为续驶里程与车速、总电流线性相关性不明显。
由上述相关性分析可知,续驶里程与电池SOC、单体温度最低值的相关性最强,所以下面选择这两个参数进行二元线性回归建模[13]。
2 续驶里程的二元线性回归分析及验证
2.1 回归模型的建立及参数辨识
SOC、单体温度最低值与续驶里程M的二元线性回归模型如下式:
M=β0+β1s+β2t
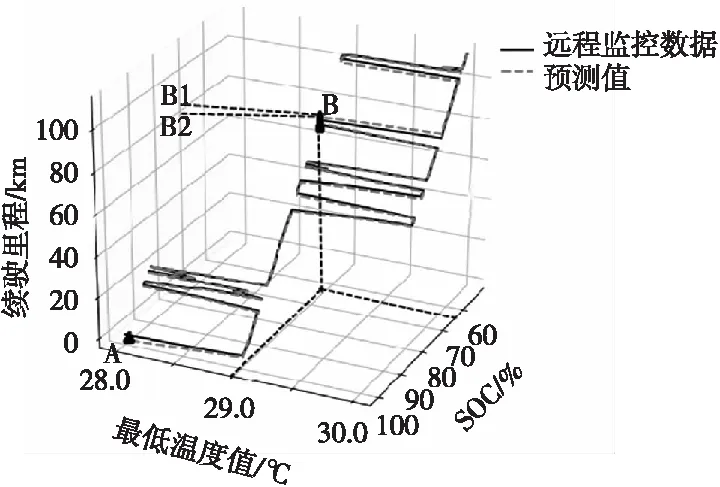
式中:s为SOC(取值区间30%~100%);t为单体最低温度值(25 ℃ 当确定回归方程后,可以利用已有的数据,根据一定的辨识方法,对回归方程中的未知参数进行辨识。最小二乘法、相关分析法、阶跃响应法、极大似然方法等是目前比较常用的辨识方法。但最小乘法在参数辨识领域应用比较广泛,在随机环境下,它并不需要知道观测数据的概率统计信息,但依然可以得到具有较好统计特性的估计结果。它既适用于动态、静态系统,也可用于离线、在线估计。 式中:Y为因变量续驶里程;X为自变量SOC和单体温度最低值的二阶矩阵。 本文用菏泽市某路纯电动城市客车2018年7月1/3/5/6/9/12/15/26/28/30日,总计10天的行驶数据,以行驶里程变化1 km为标准对除时间以外的其他数据进行平均化及标准化预处理,并用处理过的数据使用最小二乘法参数辨识,得到10天数据各自的模型参数,并求10天模型参数平均值,得到最终模型参数依次为:β0=233.883,β1=-2.432,β2=0.243。 即续驶里程预测的预测模型如下: M=233.883-2.432s+0.243t 式中:s的取值范围为[30%,100%];t的取值范围为(25 ℃,40℃)。 为了验证回归模型的预测精度,选用2018年7月18日的数据进行验证,得到预测值与远程监控数据对比如图1所示。 图1 预测值与远程监控数据对比图 在一个完整的纯电动城市客车工况中,因有驻车时间或停靠时间,此时电池温度会下降,所以导致电池温度不是一直升高,有可能会降低。 由图1中起始点A点可知,当SOC为100%、温度为28 ℃时远程监控的续驶里程为零,而预测值为2.53 km,说明在刚开始行驶阶段回归模型不准确,存在过拟合现象;由中间B点可知,当SOC为64.8%、温度为29 ℃时远程监控的续驶里程为81.6 km(即图中B1点对应值),而预测续驶里程为79.65 km(即图中B2点对应值),说明在此阶段模型存在拟合不足现象。整个过程中平均误差为0.69 km,说明在整体上模型拟合效果较好。根据数据计算,续驶里程预测值的均方根相对误差小于0.5 km,且均方根误差小于2 km。续驶里程预测值的平均绝对误差小于1.5 km。所以本模型预测精度较好。 为了验证模型适用性,选用2018年7月4日、24日2天数据进行模型验证,得到平均误差分别为1.23 km,1.01 km,平均绝对误差均小于1.5 km,所以本模型不仅预测精度较好,并且适用性也较好。 经分析,本模型虽然有时误差较大,但大部分情况下误差较小,并且预测值平均误差都在可接受范围内,能够准确预测续驶里程,并且适用性较好。因此用SOC和单体温度最低值作为自变量建立的二元回归模型对续驶里程进行预测是可行的。 1) 续驶里程预测平均绝对误差较小,说明此预测模型基本可以准确预测续驶里程。但是不足之处是误差范围较大,最大误差值达到2.53 km,说明在预测过程中偶尔会出现较大偏差。 3) 本文所建立的回归模型温度都在25 ℃以上,在低于25 ℃情况下,模型的准确性还未验证,可能在极度低温条件下不适用。且城市客车运行线路比较固定,变化情况较少,如果要包括更多的工况,还需要建立模型库。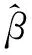
2.2 模型验证与分析
3 结 论

