基于迭代小波变换的光谱信号本底扣除方法研究

赵奉奎，徐晓美，吕立亚

(1.南京林业大学 汽车与交通工程学院，江苏 南京 210037；2.东南大学 仪器科学与工程学院，江苏 南京 210096)

光谱本底常使得净峰面积的估算结果过大和峰位估算结果偏移[1]。如能量色散型X射线荧光光谱(EDXRF)分析作为一种多元素分析技术，能够同时提供元素的定性和定量分析结果，但由于其特征峰叠加在本底之上，因此，分析时为获取特征峰信息，必须扣除本底的影响[2]。

为了扣除本底，研究人员已经提出了多种算法，一种方法是从硬件的角度出发，通过改进光路，如设计三角形光路结构抑制本底的产生[3]，更多的研究是从软件的角度对已生成的光谱进行本底扣除，常采用多项式拟合[4-5]、傅立叶变换[6]、削峰法[2,7]和小波变换(WT)[8-11]，以及近几年研究较多的神经网络等[12]。如刘察等[13-14]将信号变换到小波空间，以减轻谱信号中基线的变化。大多数方法依赖于特征峰和本底在频域分布在不同区域的特性，但当两者在频域有重合时，一般方法不易将其分开。小波变换具有多分辨率分析的特点，能够对信号进行多尺度分析，非常适合区分特征峰和本底，然而直接利用小波变换进行本底扣除容易导致光谱波形畸变。Galloway等[8]提出了一种迭代小波变换(IWT)方法，相比于传统小波变换能够对信号进行更加细化的分解，可根据信号形态区分频带重复的信号，但未研究终值迭代条件。笔者利用信息熵作为迭代小波终值条件，改进了迭代小波变换[15]方法，但计算稍复杂。

基于此，本文提出了一种更加简单的迭代终值准则计算方法，改进了基于迭代小波变换的本底扣除方法，旨在精确扣除本底，同时避免小波变换导致的波形畸变。

1 迭代小波变换理论

1.1 小波变换理论

小波变换能够在时域和频域同时进行信号分析。在小波变换过程中，利用选定的小波基，即母小波函数ψ，对信号进行分解。在实际运用时，更多的是利用离散小波变换(DWT)。为了实现多分辨率分析，还需要构造尺度函数φ。经压缩因子2j和平移因子2jn压缩平移的小波函数和尺度函数如式(1)～(2)所示：

(1)

(2)

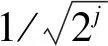
根据Mallat快速小波变换，信号f分解的逼近系数aj[n]和细节系数dj[n]可根据式(3)获得:

aj[n]=〈f,φj,n〉

dj[n]=〈f,ψj,n〉

(3)

通过与滤波器h[n]与g[n]的卷积和下采样，根据式(4)计算逼近系数aj+1[n]和细节系数dj+1[n]：

(4)

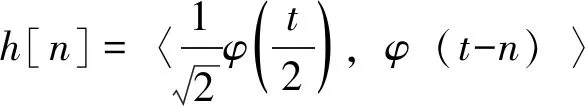
图1 离散小波分解过程Fig.1 Process of discrete wavelet decomposition

1.2 迭代小波变换理论

根据收敛定义，对正整数n，存在正整数N，当n>N时，对任意指定的ε>0，都有|fn+1-fn|max<ε，则认为f收敛。对于光谱分析，如果连续3次迭代过程中fn和fn+1之间的最大误差均小于指定ε，则认为f收敛，具体计算过程将在下述步骤中详述。

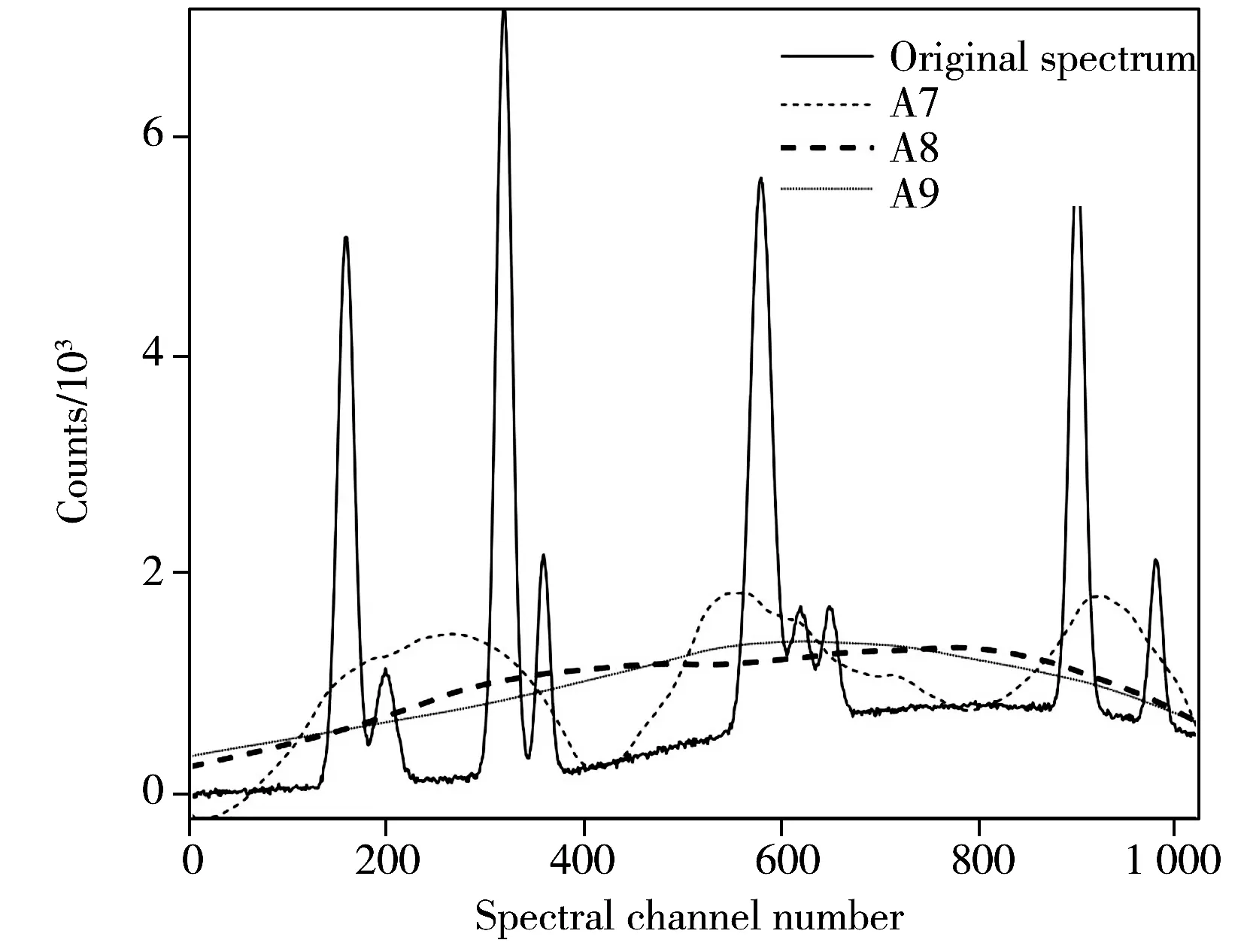
图2 在不同分解层次进行小波变换所得低频逼近图Fig.2 Approximations obtained through wavelet transform at different levels

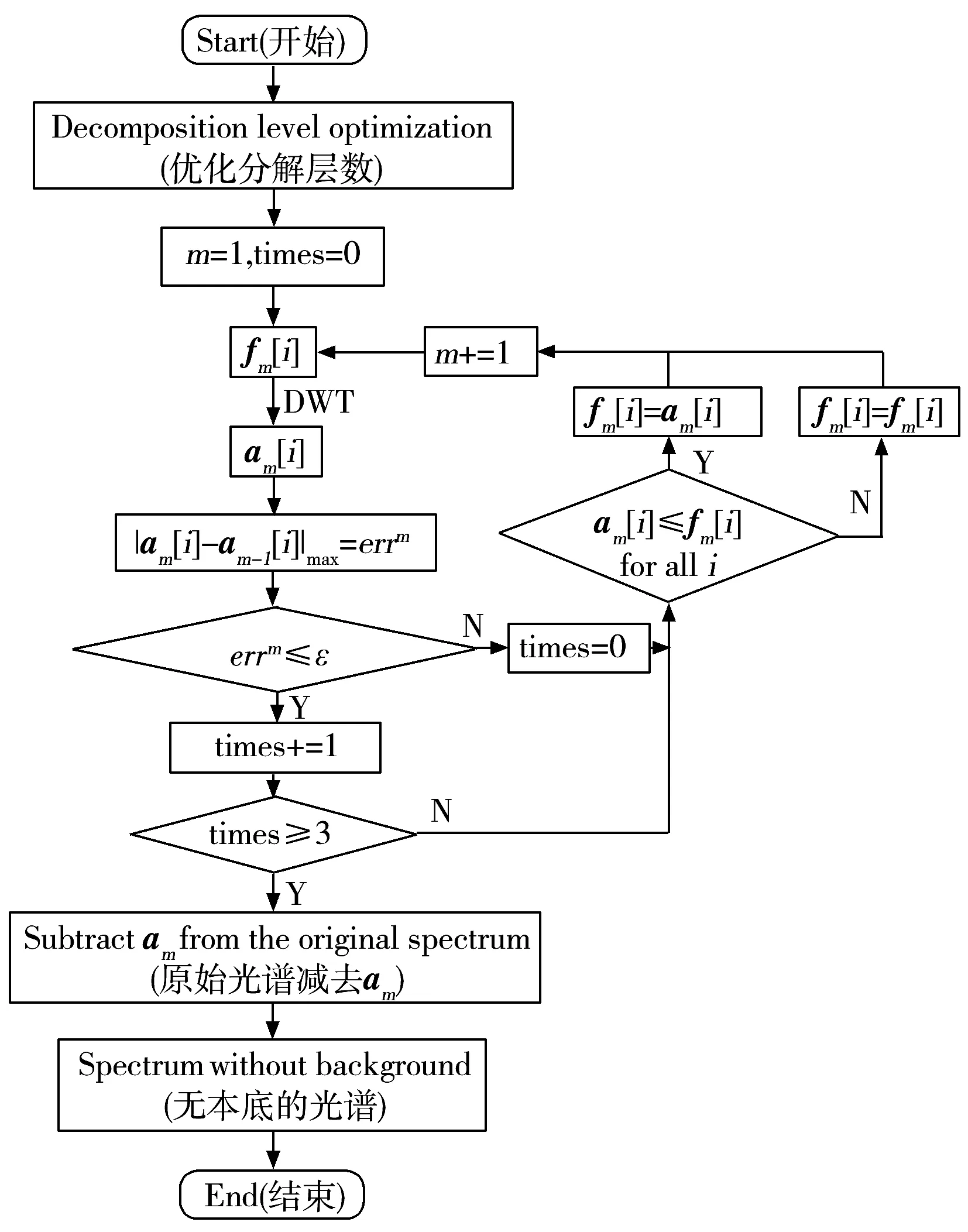
图3 基于改进迭代小波变换的本底扣除流程图Fig.3 Program flow chart of background removing method based on the improved IWT

进行迭代小波变换之前，需先确定分解层数。随着迭代小波变换过程的进行，光谱中的特征峰成分会逐步消减。为尽量减少人工干预，所有小波变换均在相同的分解层次上进行。最优分解层次的确定通过在不同分解层次上进行小波变换，比较其低频逼近的方法实现。最优的分解层次需使信号经小波分解后，所有的本底成分均包含在低频逼近中，尽管其中可能仍含有一些特征峰成分。经过试验比较，选取DB4小波基进行小波分解。信号在不同分解层次进行小波变换所得低频逼近如图2所示。图中A7、A8、A9分别表示第7层、第8层、第9层分解的低频逼近。当对信号进行较低分解层次的小波变换时，如第7层，所得低频本底振荡较为剧烈，与实际本底相差较大。当对光谱信号进行较高分解层次的小波变换时，如第8层和第9层，所得本底的变化趋势与实际本底比较一致，但第9层所得低频逼近过于平坦，所以选择第8层作为最优分解层次。在后续的迭代小波变换过程中，均在第8层对信号进行小波分解。

基于迭代小波变换的本底扣除过程如图3所示，具体流程如下：

①fm[i]用来表示经m-1次迭代小波变换后的光谱，其中m≥1为整数，表示迭代次数，i表示光谱通道，原始光谱标记为f1[i]。

②在优化分解层次上对fm[i]进行小波分解，将得到的逼近系数am[i]作为第m次估计的本底。

③计算|am[i]-am-1[i]|max=errm，a0与f1[i]相等，表示原始光谱。将errm和用户指定的误差ε进行比较，比较次数由times进行索引，times初始值为0。当对所有的通道均存在errm<ε时，表示相邻两次所估计的本底足够一致，将times=times+1，跳至步骤④，否则，重置times=0，并转至步骤⑤。

④如果times≥3，则连续4次小波变换所得估计本底足够一致，认为所得估计本底已经收敛，最后一次小波变换所得低频逼近am[i]作为最终估计的本底，从原光谱中减去am[i]即可实现本底扣除。

⑤比较所有通道值的fm[i]和am[i]，将各通道最小值替换fm[i]，即：

(5)

通过削去较大值的方法，迭代地去除低频逼近中的特征峰成分，令m自增，转至步骤②。

2 实验结果与讨论

2.1 仿真光谱的本底扣除

为验证算法的有效性，首先利用仿真光谱对算法进行分析。已有研究表明，EDXRF光谱中的特征峰可由高斯峰表征，本底可由解析函数表征[1]。因此，本研究采用高斯峰为特征峰，多项式函数为本底，构建仿真光谱。

为验证算法是否对噪声敏感，在光谱上增加了信噪比为38 dB的噪声，仿真光谱如图4A所示。

根据“1.2”所述小波分解层次选择方法，选取第8层为最优分解层。相邻2次小波分解所得errm见表1。结果显示，随着迭代过程的进行，errm明显衰减。由于最大峰高7 000，选取ε=10可以认为2次所得本底足够一致。10次迭代后，连续3次errm<ε，表明所得估计本底已近似收敛。

Iteration number(m)12345678910errm6 12060018067301711864

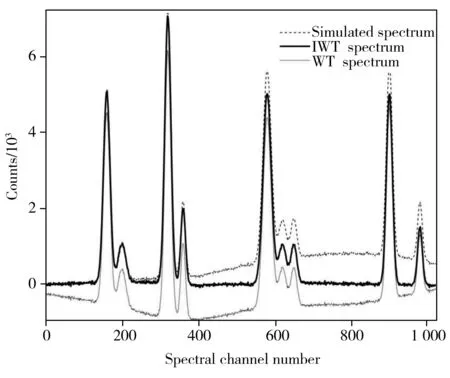
图5 迭代小波变换估计的光谱与传统小波变换估计的光谱对比Fig.5 Comparison of the estimated spectra with IWT and non-iterative WT

迭代过程见图4B，图中第1个估计本底(1st Estimated bakground)表示第1次小波变换后得到的本底。由图可知，第一次小波变换得到的本底与实际信号本底相差很大。随着迭代小波变换的进行，所得估计本底与仿真光谱的本底逐渐靠近。7次迭代后，所得估计本底收敛到仿真光谱本底。从原始仿真光谱中减去估计的本底即可实现本底扣除，去除本底后光谱见图5(IWT spectrum)。同时也可以看到，在存在噪声的前提下，该算法仍能够准确估算本底。

作为对比，对该仿真光谱利用多项式拟合法和传统小波分解进行本底估计。利用DB4小波对仿真光谱在第8层进行分解，不进行迭代，小波逼近系数作为估计的本底。实验发现，从原始光谱中去除小波变换估计的本底使光谱产生了较大畸变(图5 WT spectrum)。相比之下，迭代小波变换能准确扣除本底，且未引入波形畸变。

2.2 实验光谱的本底扣除

为进一步验证算法的有效性，利用迭代小波变换对EDXRF光谱仪所测光谱进行实验。光谱仪采用Si-Pin探测器，高压为45 kV。通过对光谱的观察和实验，选择DB6在第8层对光谱进行分析。光谱迭代分解过程见图6A。由图可知，经一次小波分解后，所得估计本底与光谱实际本底相差较大，而经小波分解迭代6次后，所得估计本底趋于收敛。

迭代小波变换过程中的errm列于表2中，考虑到特征峰最高值为8 000，ε=10时认为所得估计本底足够接近。经7次迭代后，err7<ε，9次迭代后，可认为迭代过程收敛。表中数据显示的本底变化趋势与图6A中一致。

表2 实验光谱相邻两次估计本底误差Table 2 Errs of two consecutive estimated backgrounds of the experimental spectrum

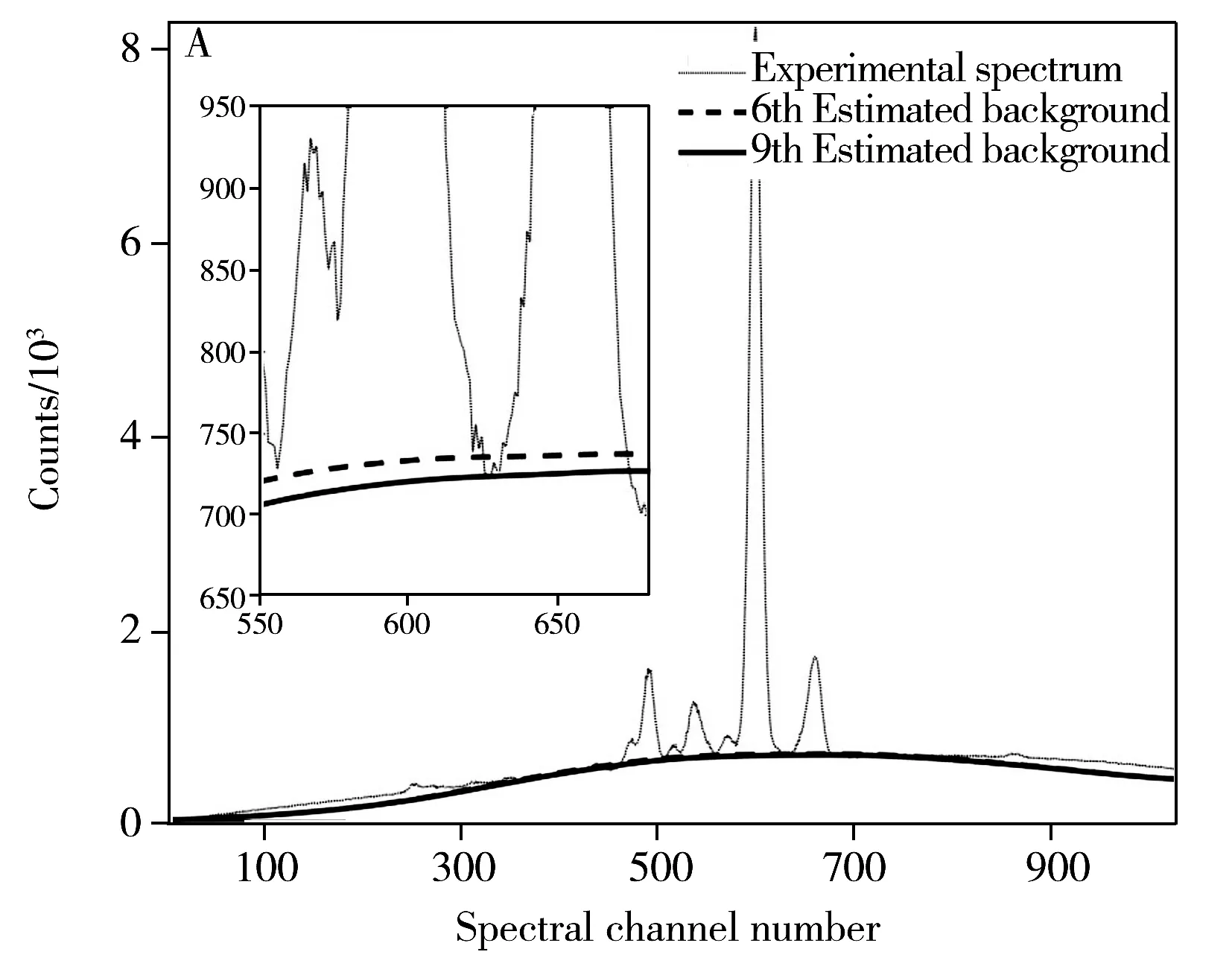
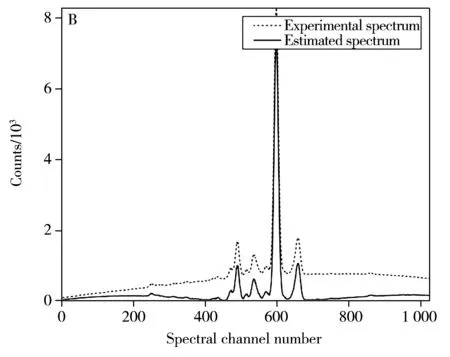
图6 实验光谱迭代小波变换过程(A)和原始实验光谱与扣除本底光谱对比图(B)
Fig.6 Process of iteration for the experimental spectrum(A) and comparison of the original spectrum and background-subtracted spectrum(B)

从原始光谱中减去第9次小波变换所得估计本底，即可去除本底。原始实验光谱与本底扣除光谱对比如图6B所示，由图可知，本底已完全扣除，去除本底后的光谱基线与水平坐标非常接近，且波形未发生畸变，峰位未偏移，即使弱峰也保持完整，因此该算法也为低含量元素的分析奠定了基础。

3 结 论

本文基于迭代小波变换的本底扣除改进算法提出了一种迭代停止标准。该算法通过对仿真光谱和实验光谱的分析，准确扣除了光谱本底，证明了算法的有效性，为光谱净峰面积的计算和峰位的计算奠定了基础。与传统小波变换本底扣除法相比，该算法能够对信号进行更加精细的分解，从而分离特征峰和本底重复的部分，且不会导致波形畸变。与多项式拟合法相比，本底扣除结果更加准确。本研究迭代的思想也可由傅立叶或多项式拟合来实现，为光谱分析提供了有力的工具。