PAM仿袋鼠腿悬架仿真建模及垂向参数特性研究

宋 勇,车江轩,孙大刚,李俊鹏,刘世闯

(太原科技大学 机械工程学院,太原 030024)

车辆悬架是弹性联接车架与车桥(或车轮)的缓冲减振装置,其品质对车辆的平顺性和稳定性有着重要的影响。随着车辆的广泛应用及人们对高品质车辆的追求,尤其是高舒适性能的追求,使车辆悬架结构设计变得更为困难[1-2]。研究发现,自然进化而来的袋鼠腿部结构使其跳跃行走于复杂地形时,具有奔跑速度快、越障能力强、运动稳健等特点[3-5]。受此启发,本文提出了一种PAM[6](气动人工肌肉,Pneumatic Artificial Muscle)三连杆等骨骼比例仿袋鼠腿车用悬架。该悬架主体结构由仿生大腿-小腿-足骨骼、仿生髋-膝-踝关节及仿生大-小腿-跟腱肌肉、肌腱构建而成。

PAM是一种将气动压力转换为机械力的装置,它结构简单、质量轻、动态特性好、强非线性、输出力/自重比大、噪音小,是一种理想的仿生驱动元件。故本文采用PAM模仿袋鼠腿肌肉自适应调节功能以实现仿袋鼠腿悬架姿态的实时非线性调节。

本文将构建出的PAM仿袋鼠腿悬架应用于车辆中,并对影响车辆舒适性的悬架垂向参数特性进行探究。建立PAM仿袋鼠腿悬架1/4车辆Adams仿真模型;以路面不平度为激励,采用模糊控制策略控制PAM输出力,实时调节悬架姿态,研究其垂向参数特性[7];进行被动、被——主动模式下的悬架垂向特性仿真,对比分析其在两种模式下的缓冲减振性能。

1 PAM仿袋鼠腿悬架的构建及工作原理

本悬架结构的设计思路是:在通过模仿袋鼠为适应自然环境而演变进化出的腿部结构,设计一种仿袋鼠腿车用悬架[8-9]。模仿袋鼠腿部结构的基础上[10-11],尽可能的简化机械结构,由袋鼠腿部肢体结构构建出的等比例仿生大腿骨杆、仿生小腿骨杆、仿生足骨杆,特别在足骨杆处构建以踝关节为支撑点的一个杠杆结构,形成了与袋鼠足部相同的特殊结构;所构建的仿生关节在满足机械运动要求的前提下应尽可能少,在仿生骨杆连接处构建仿生髋-膝-踝关节;将袋鼠腿部肌肉、肌腱等效为阻尼减振器、弹簧;主动元件为气动人工肌肉,可模仿袋鼠腿部运动姿态调控仿生关节转角,可根据路面激励调整出不同减振姿态[12-13];其具体元件构建形式如图1所示。

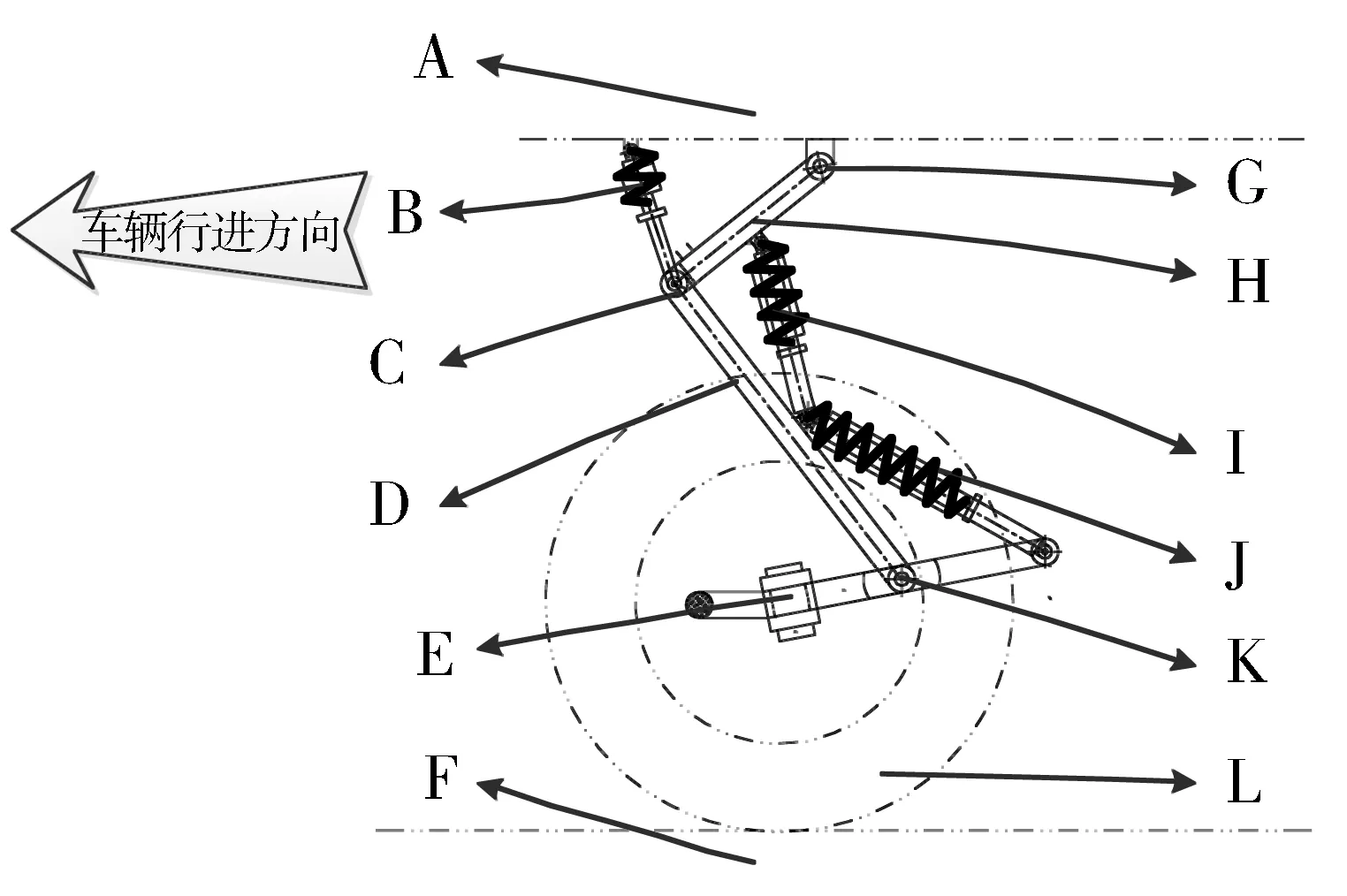
图1 PAM仿袋鼠腿悬架Fig.1 PAM bionic kangaroo legsuspension mechanism

其中:A表示车身;B表示仿生大腿肌肉肌腱弹簧、阻尼器与大腿PAM;C表示膝关节;D表示仿生小腿骨杆;E表示主销与车轮连接处;F表示地面;G表示仿生髋关节;H表示仿大腿骨杆;I表示仿生小腿肌肉肌腱弹簧、阻尼器与小腿PAM;J表示仿生跟腱肌肉肌腱弹簧、阻尼器与跟腱PAM;K表示仿生踝关节;L表示车轮。

2 PAM仿袋鼠腿悬架元件参数计算

2.1 仿生连杆长度与仿生关节转角计算

根据PAM仿袋鼠腿悬架构建形式,并结合相关文献记录[14-15],袋鼠的大腿、小腿、足的长度分别约占该腿部总长度的23%、46%和31%.因此按照袋鼠腿部比例设计实现仿生悬架的形态与结构仿生,各仿生连杆的比例为1∶2∶1.35.其中仿生连杆的长度与悬架的纵向运动空间相互关联,仿生杆件转角与夹角可由余弦定理计算。

仿生连杆比例关系:

LOB∶LAC∶LCD=1∶2∶1.35

(1)

纵向运动空间表达式:

LOAsinθ1+LACsinθ2+LCDsinθ3=H

(2)

仿生肌腱弹簧角度变化:

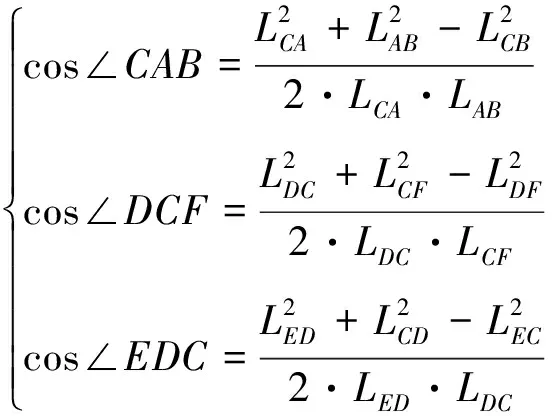
(3)

其中:LDC为仿大腿骨连杆,LCA仿小腿骨连杆,LOB仿足骨连杆的长度;LEG,LGF,LFB分别为仿生大腿、小腿和跟腱肌肉肌腱弹簧的长度;点D,C,A分别为各固定铰点间的位置;具体位置如图2所示。

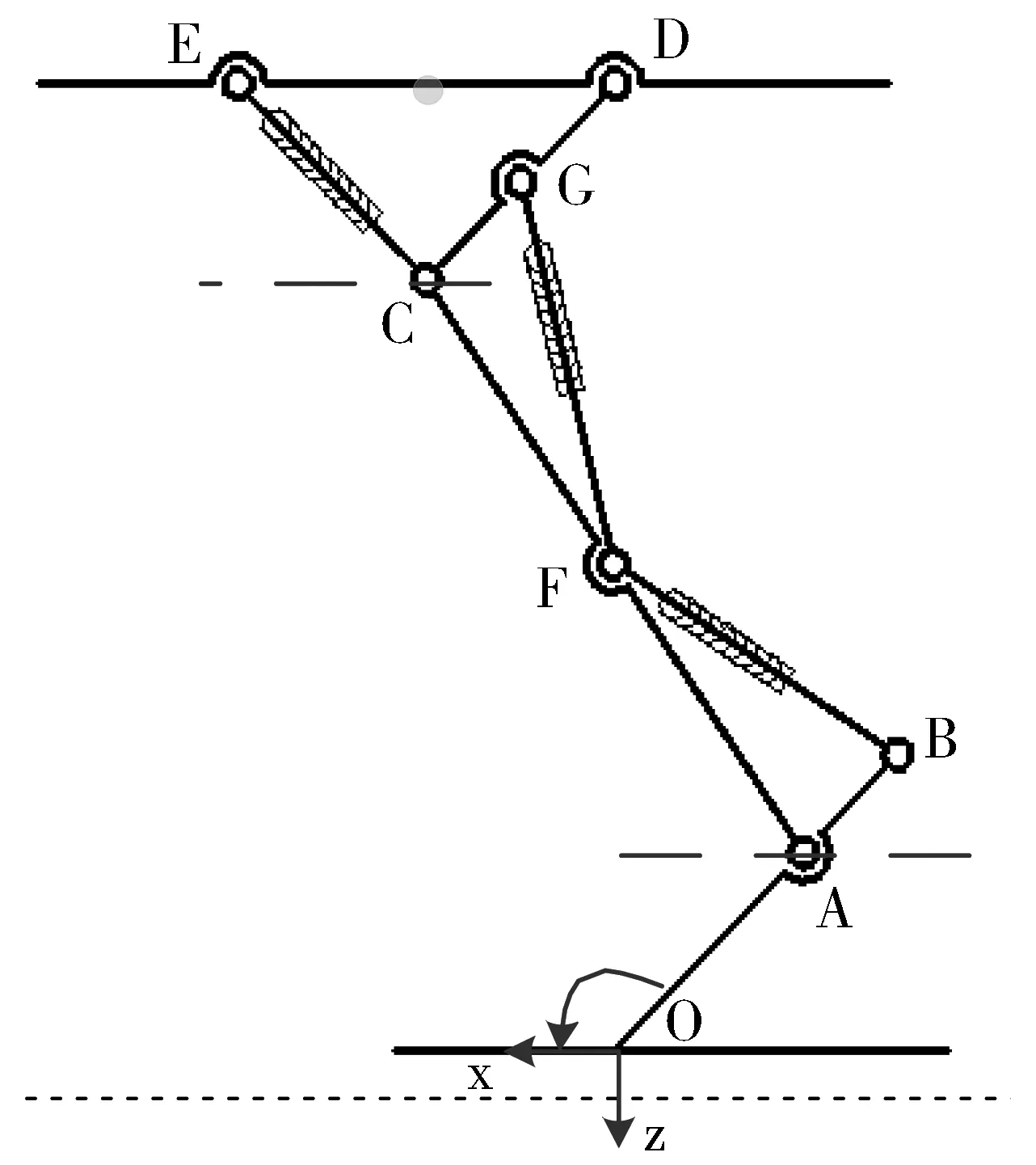
图2 PAM仿袋鼠腿悬架简图Fig.2 PAM bionic kangaroo leg suspension layout

2.2 仿袋鼠腿悬架PAM参数计算

气动人工肌肉是一种新型的仿生气动执行机构[16-17]。该机构是一种拉伸执行机构,模仿肌肉运动,在被——主动工作模式下,可驱动连杆围绕仿生关节转动,实现姿态调节,并保持良好的减振姿态。

本悬架设计中将气动人工肌肉等效为变刚度的作动器,其轴向输出力的函数关系式为:

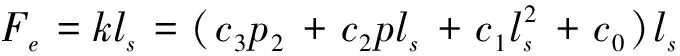
(4)

式中,k为气动人工肌肉的刚度;p为充气压力;ls为伸长量;c1,c2,c3,c4分别为k、p和ls之间的系数。橡胶套筒的弹性力Fs为:

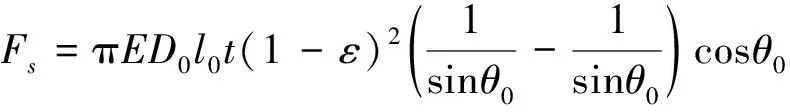
(5)

式中:

(6)

D0,θ0,l0分别为充气前气动人工肌肉的初始直径、初始纤维角度和初始长度;l为其自由长度;E为橡胶筒的弹性模量;t为气动人工肌肉橡胶筒的厚度;ε为PAM收缩率。单个气动人工肌肉的收缩力方程为:

U=Fe-Fs

(7)

2.3 仿袋鼠腿悬架弹簧刚度求解

变角度组合减振弹簧[18-19]工作简图如图4所示,在本论文研究当中,根据仿袋鼠腿车用悬架的构建形式,仿生大腿骨杆与仿生小腿骨杆上均布置有两根仿生肌腱弹簧,悬架在外部激励作用下被动减振时,仿生踝关节的转动,与布置的仿生肌腱弹簧将会使仿生髋关节与仿生膝关节发生转动,此时仿生肌腱弹簧的受力角度将发生变化,于此同时产生的等效刚度也会随之改变。实现悬架的等效弹簧刚度在不同范围间的变换,另外两处的变角度组合减振弹簧也有相同规律。

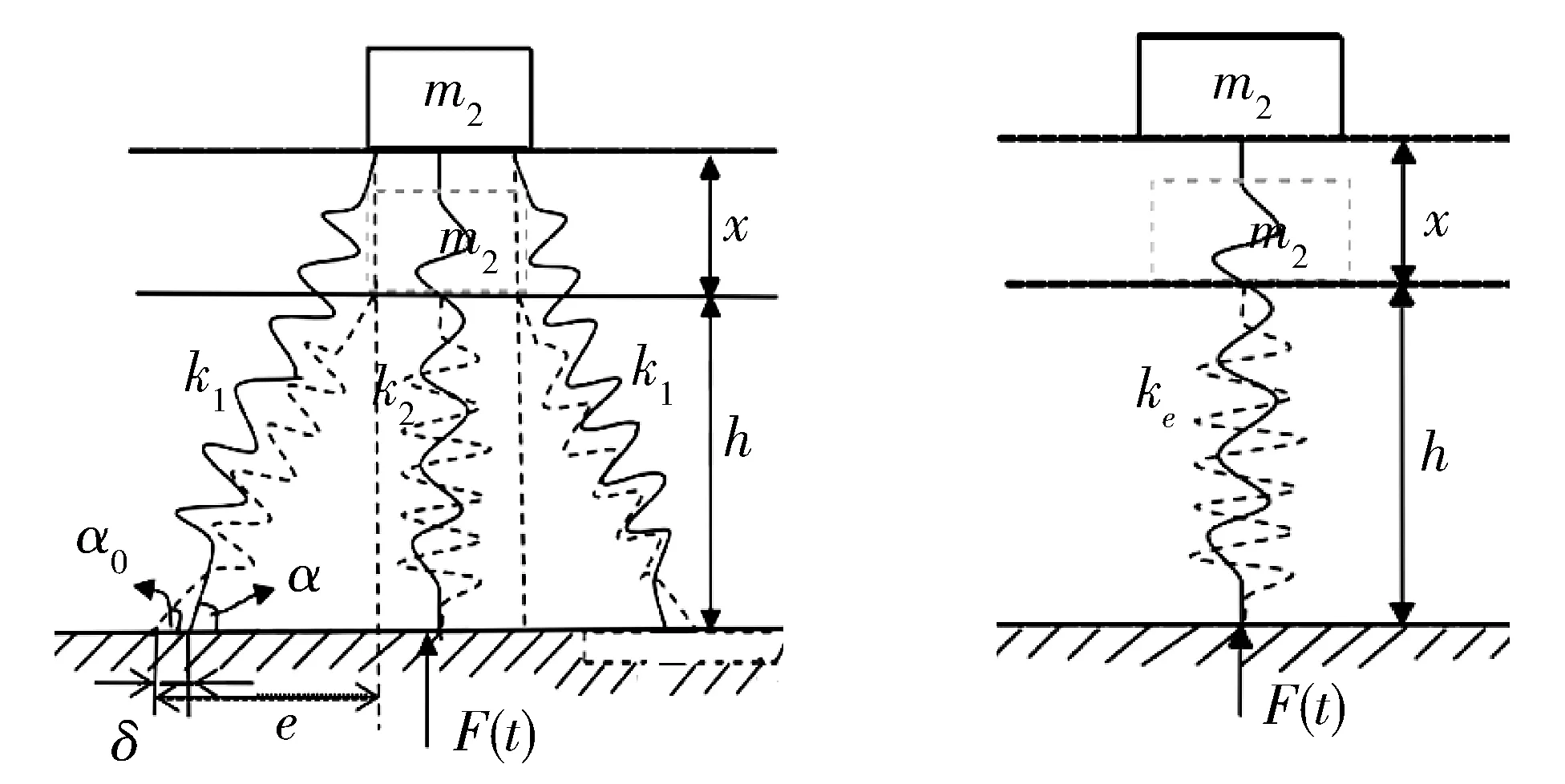
图3 变角度组合减振弹簧工作示意图Fig.3 Variable angle combination damping spring working diagram

其中:m2为簧载质量;x为激励使簧载质量产生的垂直位移量;α0为弹簧初始安装倾角;l0为侧倾弹簧初始长度;α为瞬时弹簧倾角;l为侧倾弹簧在工作过程中的长度;δ为偏移距离;h为静平衡时组合弹簧的高度;ke为等效弹簧刚度;e为侧倾弹簧水平投影长;F(t)为外力。

通过受力分析,可得:

F=k2x+2k1(l-l0)sinα=

(8)

式中:

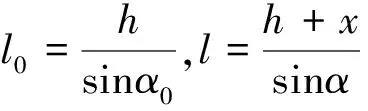
(9)

推导出等效刚度表达式:

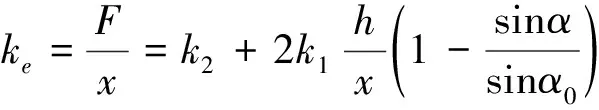
(10)

式中:

(11)

将式(11)带入(10)后,等效刚度ke的函数表达式如下:

(12)

2.4 仿袋鼠腿悬架阻尼器阻尼系数的确定

根据振动理论和工程经验[20],确定ζ值后,悬架阻尼的匹配关系可由式(13)确定:

(13)

上式中:ζ为悬架系统阻尼比;C为悬架减振器的等效阻尼比;K为悬架刚度;m为簧载质量。

3 PAM仿袋鼠腿悬架仿真建模

3.1 模型假设

本文对仿袋鼠腿车用悬架机构进行仿真建模分析时,重点分析的所着地减振阶段。由于袋鼠腿的实际结构非常复杂,很难用精确的数学模型来描述它,在仿真建模前合理的对其结构进行简化并进行假设:

(1)假设各仿生骨骼杆件都为刚性构件,且质心都在中点处。

(2)假设各袋鼠腿部的肌肉肌腱,可由仿生肌腱肌肉弹簧阻尼器代替,且都由三部分组成,仿大腿肌腱肌肉弹簧阻尼器、仿小腿肌腱肌肉弹簧阻尼器和仿跟腱肌腱肌肉弹簧阻尼器,悬架被——主动模式所布置的PAM也在相同位置。

(3)假设袋鼠腿部的关节可由仿生铰关节代替,在仿袋鼠腿车用悬架中分别布置仿生髋关节、仿生膝关节和仿生踝关节。

3.2 运动副设置

由于本文所研究的是悬架系统在垂向平面内的运动特性,故在建立仿袋鼠腿悬架仿真模型时由于仿生连杆构件间的约束设置,袋鼠腿部三自由度的球面髋关节在仿生悬架中可视为单自由度的铰接转动(副)仿生髋关节;同样袋鼠腿部的膝关节与踝关节也均视为单自由度的铰接转动(副)仿生膝、踝关节;为了更好的施加来自路面的冲击激励,搭建地面平台,施加垂向位移激励,添加路面激励移动(副)。

3.3 模型参数的确定

本文所设计的悬架结构,为了突出其具有与袋鼠腿相类似的运动特性与优点,选取中大型越野车辆作为参照模型,选取静平衡离地高度为0.55 m的初始位置,分别定义悬架的最大垂向最大下跳压缩与最大上升回弹范围分别设定为0.1 m,1/4整车簧载质量为450 kg,本文主要采用查阅建模法和计算法确定模型的车辆参数,结合前述小节中的计算方法。具体1/4整车模型参数见表1.

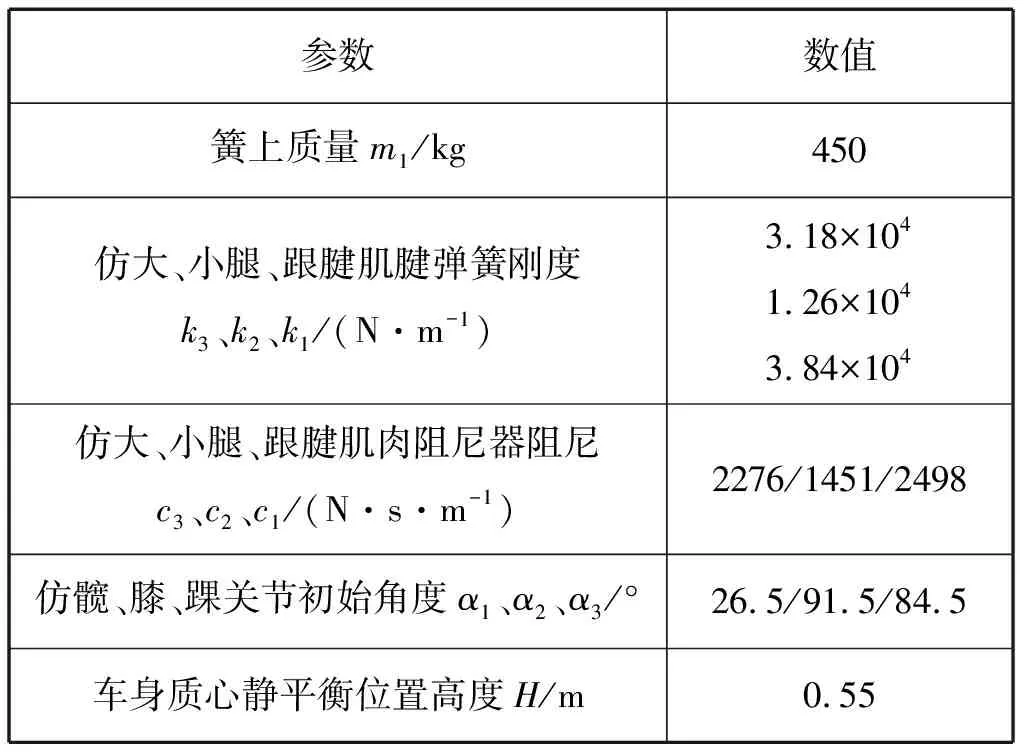
表1 仿袋鼠腿悬架模型参数Tab.1 Imitation kangaroo leg suspension model parameters

初始静平衡状态下的各角度数据参考袋鼠稳定站立时的各角度参数,角度变化选取袋鼠腿落地和起跳两个过程的部分范围。具体参数见表2.

表2 关节角度参数Tab.2 Joint angle parameter range

仿生连杆的长度可由杆长比例结合车身静平衡位置的悬架高度计算出长度,最后圆整数据见表3.

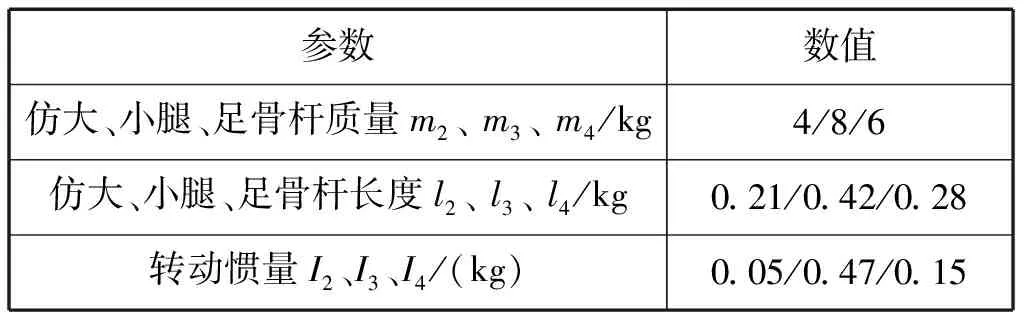
表3 仿生骨杆参数Tab.3 Biomimetic bone parameters

由上述参数对处于静平衡位置时的1/4仿袋鼠腿车用悬架进行Adams仿真建模,所建仿真模型具体如图4所示。

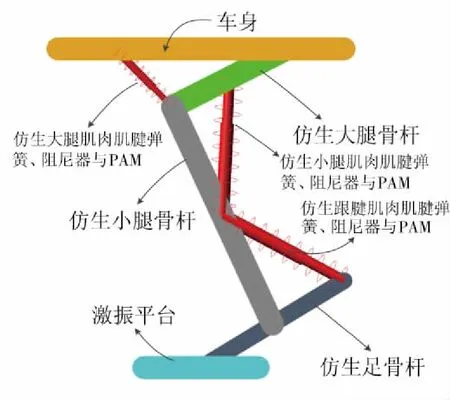
图4 1/4仿生悬架仿真模型Fig.4 1/4 Bionic suspension simulation model

4 PAM仿袋鼠腿悬架垂向参数特性研究

4.1 控制策略的制定

为了实现仿袋鼠腿悬架姿态的实时调节,且考虑到PAM的强非线性,本文模仿袋鼠腿跳跃运动姿态,采用自适应模糊算法对本悬架进行控制策略制定。本悬架设有两种工作模式,分别为被动和被——主动工作模式;悬架被动工作时,大、小腿和跟腱气动人工肌肉不工作,对外无输出力;悬架被-主动工作时,大、小腿和跟腱气动人工肌肉对外输出收缩力U1、U2、U3。车辆行驶时,通过预设的专家系统路面不平度判断域及车身加速度判断域进行模式选择与切换[21-22],设置三个模糊控制器分别控制大、小腿和跟腱气动人工肌肉,将控制经验总结成模糊控制规则,并根据系统输入值实时调整PAM的收缩力。

设定车身加速度a及路面激励x4为模糊控制器的输入,通过模糊控制规则的对应关系,调节PAM输出力调整减振姿态,使悬架输出具有良好的动态性能。输入、输出变量的隶属函数选为高斯型隶属函数。具体模糊控制规则见表4-表6.

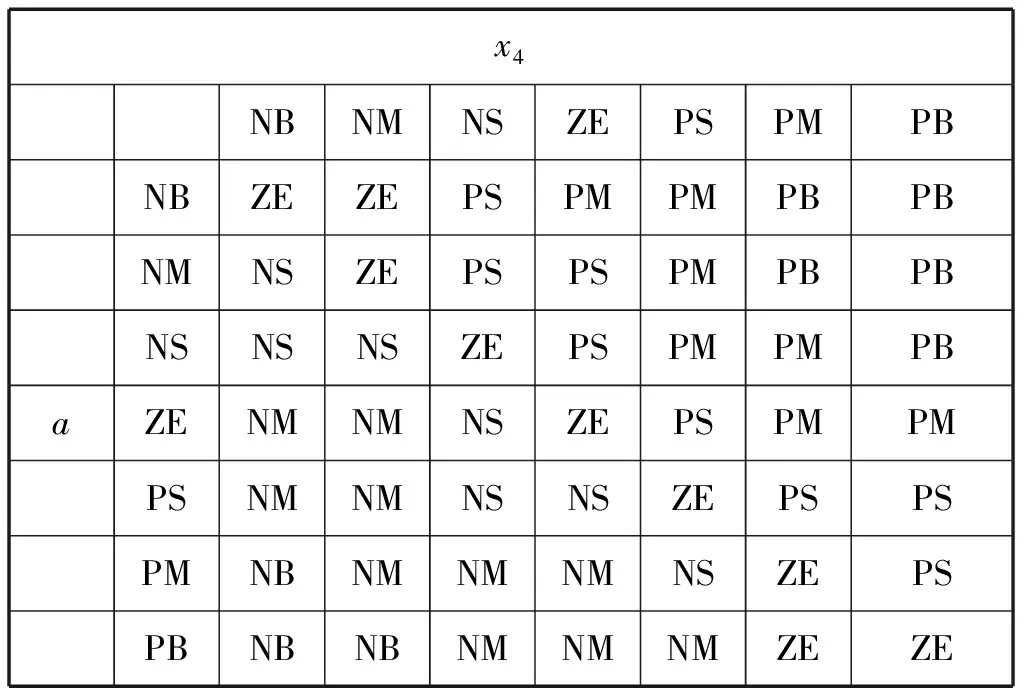
表4 U1模糊控制规则表Tab.4 U1 Fuzzy control rules table

表5 U2模糊控制规则表Tab.5 U2 Fuzzy control rules table

4.2 垂向参数特性仿真

采用MATLAB & Adams联合仿真[23],建立1/4车辆悬架舒适性仿真模型,并用三个模糊控制器对U1、U2、U3进行自适应控制。具体仿真参数见表1-表6.

表6 U3模糊控制规则表Tab.6 U3 Fuzzy control rules table

本文主要从以下三个方面进行仿真[24-25]:(1)悬架——动态特性;(2)悬架——控制特性;(3)悬架——速度特性。对装有该悬架的某型车辆分别在脉冲、阶跃、C、D级路面激励[26-27]下,以低(车速16.67 m/s)、高速(车速25 m/s),进行被动、被-主动模式下的时域仿真。经仿真计算发现,上述三种输出特性变化规律基本一致,因篇幅有限,仅给出如下仿真结果,如图5a-5g所示。图5a-5d为车辆以10 m/s的速度通过脉冲路面激励时,悬架被动工作模式下的动态特性;图5e为车辆以10 m/s的速度通过阶跃路面激励时,悬架被动与被-主动工作模式下的车身动位移图;图5f-5g为车辆分别以不同速度(低速16.67 m/s与高速25 m/s)通过D级随机路面激励时,悬架被动与被-主动工作模式下的车身动位移与车身加速度图。

具体垂向参数仿真数据结果如表7-8所示.

根据图5及表7-8所列数据,进行仿真结果分析[28-30]。分析悬架——动态特性(图5a-图5d)发现,在脉冲路面激励条件下,仿生踝关节的转角变化与仿生跟腱的变形量均最大,并且与袋鼠腿部运动时的动态特征相似,实现了生物结构向工程结构的仿生设计并保留了袋鼠运动减振缓冲的特征,同时仿生悬架车身动位移下降70%,说明悬架被动模式处理瞬时脉冲激励效果较好,车身加速度在上凸激励处是下凹激励处的50%,表明悬架在应对凸起路面时的抑振效果优于凹陷路面,提高了车辆行驶稳定性;按悬架——控制特性分析(图5e-图5g),相对于被动模式,被-主动模式能够随着路面激励的增大及车速的增加有效降低车身动位移均方根、车身垂向加速度均方根,此结果表明所制定悬架模糊控制策略的有效性;从悬架——速度特性分析(图5f-图5g),路面激励相同时,随着车速的增加,两种模式下的悬架减振效果均表现出增大趋势,特别是在中等激励下的抗振动冲击效果明显,表明悬架结构设计较为合理。此结果显示PAM的实时调节使悬架能够自主适应不同路面激励的振动冲击。

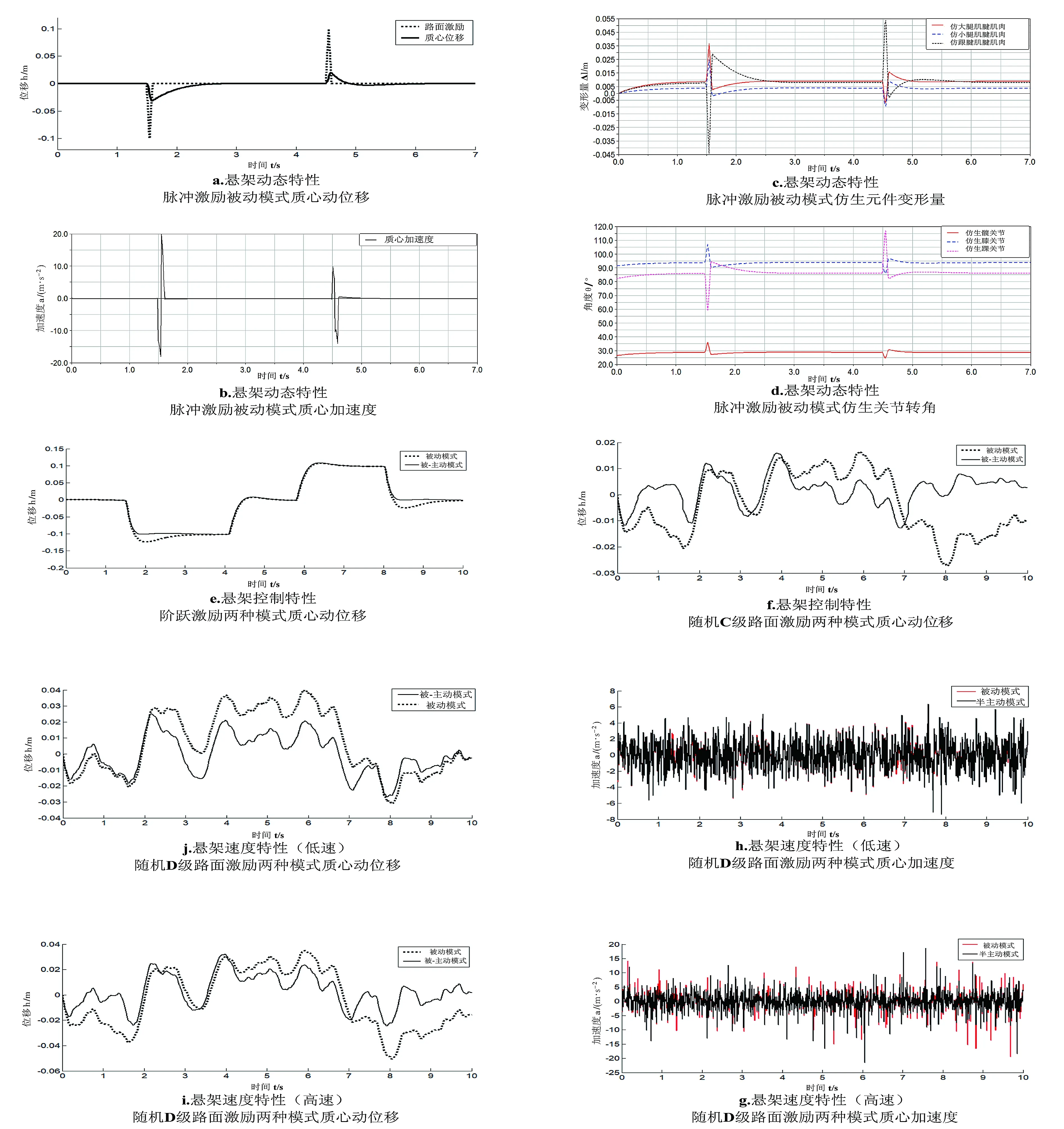
图5 悬架垂向参数仿真Fig.5 Vertical parameter simulation of suspension

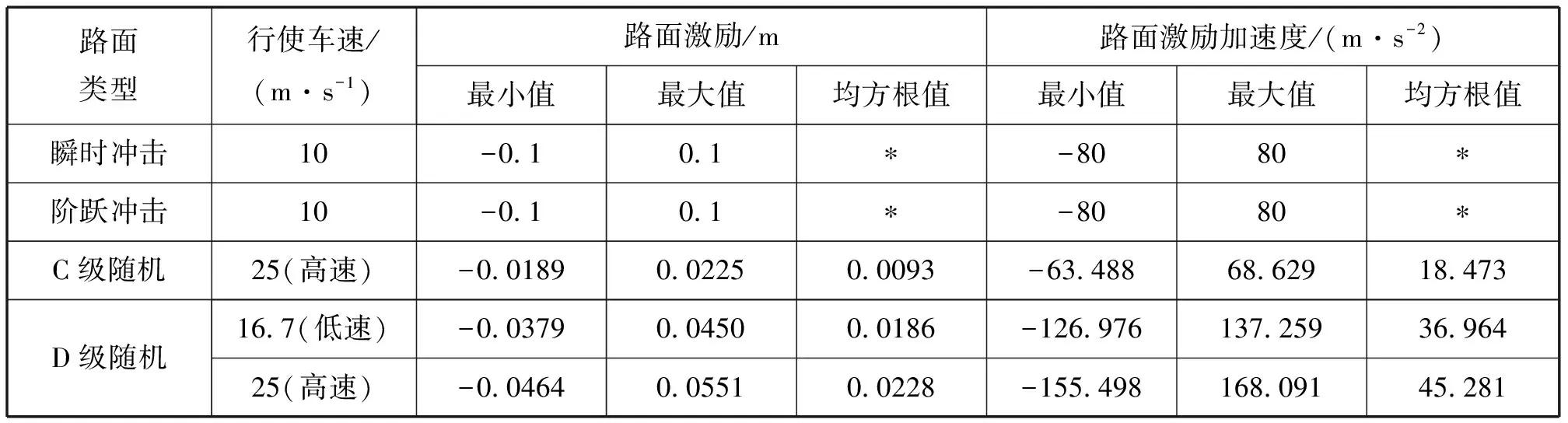
表7 路面动态参数Tab.7 Road surface dynamic parameters

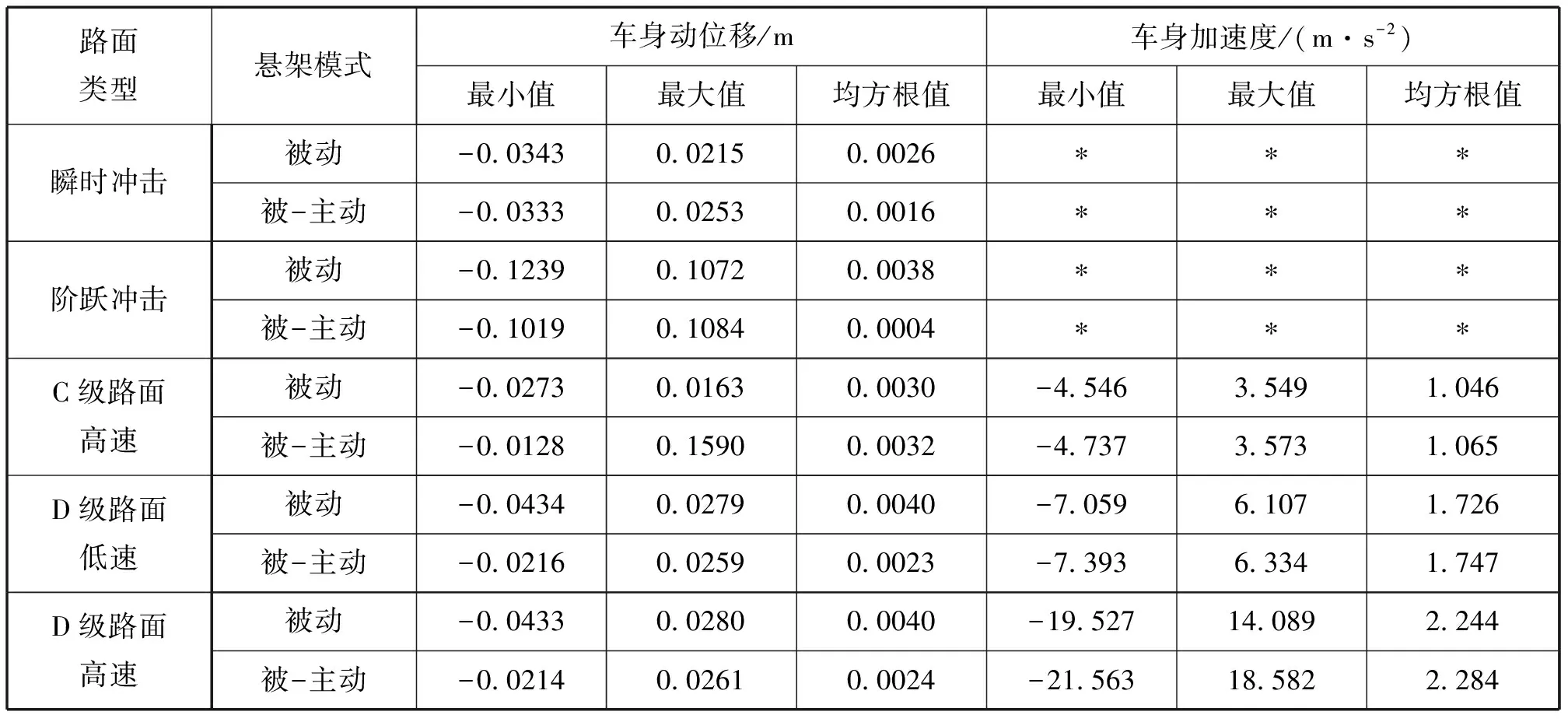
表8 车身动态参数Tab.8 Body dynamic parameters

表8具体来说,在被-主动工作模式下的车身动位移与车身垂向加速度的波动区间分别下降47.3%和13.5%;当车速分别为16.67 m/s和25 m/s通过D级路面时,车身垂向动位移均方根值下降16.3 mm、20.4 mm、;当车辆以16.67 m/s行驶在C、D级路面时,车身动位移均方根值相对路面激励均方根值分别为34.4%和13.7%;此外发现,当高速通过C级路面时,悬架两种工作模式下的车身动位移均方根值与车身加速度均方根值相同,说明在微小振动条件下相较于被动工作模式,被-主动工作模式对悬架的减振效果提升并不明显;然而,相同速度随着路面不平度的增加,悬架两种模式的位移传递率随着激励的增加而降低,最小为44.7%.而且处于较大负向激励时,悬架被动模式的位移传递率接近100%,表明悬架被动模式在较大负向激励下减振效果有一定的下降,被-主动模式下的悬架减振效果保持较好无明显下降;但在先同路面激励不同速度下,悬架两种模式垂向动位移的减振规律没有明显变化。然而车身垂向加速度幅值有均有所放大,最大幅值可达300%.同时在低速D级路面条件下两种模式的加速度范围几乎相同,而速度提升至高速时,明显被-主动模式下的车身垂向加速度变化比被动模式高20%左右,均方根值变化较小。表明被-主动模糊控制下的PAM出力较为频繁且应对高速大振动冲击减振效果明显,且可主动调节悬架动刚度以提高车辆行驶的稳定性。

5 结论

通过对袋鼠腿部肢体及其功能的剖析与提炼,构建出基于PAM的等骨骼比例仿袋鼠腿悬架结构;建立其三连杆被-主动控制仿真模型;制定出一种自适应被-主动模糊控制策略,并对其进行舒适性仿真分析,得到以下结论:

(1)从悬架——控制特性、速度特性及动态特性分析发现,所提出的PAM仿袋鼠腿悬架在被-主动模糊控制下能够自主适应不同路面激励的振动冲击,表明悬架结构设计的合理性、模糊控制策略的有效性及良好的抗振动冲击性能,同时也验证了所建仿真模型的正确性。

(2)从位移传递特性发现,被-主动模式下的悬架减振效果良好,且可主动调节动刚度使车辆平稳行驶,验证了自适应模糊控制策略的有效性;被动模式下的悬架减振效果一般,当处于凹陷路面激励下,振幅有所放大,说明其结构参数有待进一步优化。