纳米流体液膜蒸发自组装双尺度沉积结构三维模拟*

高超 袁俊杰 曹进军 杨荟楠 单彦广

(上海理工大学能源与动力工程学院,上海市动力工程多相流动与传热重点实验室,上海 200093)

纳米流体液膜在自然状态下蒸发干燥后除了形成单一尺度的网状连续结构、枝状分形结构以及微尺寸环结构等沉积结构,还会形成双尺度细胞网络沉积结构和双尺度纳米粒子环状沉积结构.为了更直观地研究纳米流体液膜双尺度沉积结构的形成机理,本文在二维动力学蒙特卡罗模型的基础上,建立了三维动力学蒙特卡罗模型,并加入了耦合溶剂蒸发率的动态化学势,成功模拟出了双尺度细胞网络沉积结构和双尺度纳米粒子环状沉积结构,并讨论了动态化学势中化学势锐度与流体临界蒸发率对纳米流体液膜蒸发自组装双尺度沉积结构的影响.模拟结果与文献中的实验结果吻合良好.

1 引 言

近年来纳米流体在微纳制造、信息技术、生物医学等领域得到了广泛的应用[1-6].除了强化传热方面的研究外,纳米流体的蒸发干燥及沉积结构的理论研究和应用也日益受到关注[7-11].纳米流体在自然蒸发时,悬浮在流体中的纳米粒子会受到运动阻力、布朗力、粒子间作用力、重力等作用力[2,4,5,12-15]的影响,运动规律极其复杂.当纳米粒子从基液中沉积到基板上时,可以自发地形成各种各样的沉积结构.这些沉积结构包括蠕虫状结构、网络状连续结构、树枝状分形结构以及微尺寸的环结构等[14-26].通过理论模拟预测纳米流体蒸发后形成的沉积结构,有助于揭示纳米流体蒸发自组装机理并推动调控自组装过程方法的发展.

2003年,Rabani等[16]在二维伊辛模型[17]的基础上通过系统化学势得出的系统能量变化建立了适用于纳米流体蒸发干燥及沉积结构的二维动力学蒙特卡罗(kinetic Monte Carlo,KMC)仿真模型,能够再现纳米粒子的自组装模式,得到了和实验相符合的结果,从而开创了使用KMC方法模拟纳米流体蒸发干燥及沉积结构模拟的研究.Crivoi和Duan[18]在二维KMC方法的基础上对开放边界纳米流体液膜进行了模拟研究.Zhang等[19]则使用了随时间和位置变化的函数来表达液体的有效化学势,从而使二维KMC方法可以用于模拟纳米流体液滴的蒸发沉积过程.Martin等[20]则对含有钝化金纳米粒子的纳米流体液膜的沉积结构进行了实验研究,并与利用KMC方法模拟的结果进行了比较分析,发现马兰戈尼对流并不是网状沉积结构形成的必要条件.之后,Stannard和Martin等[21,22]通过实验发现纳米流体液膜的沉积结构具有双尺度现象,即沉积结构中较大尺度与较小尺度的沉积结构同时出现,并均匀地交错在一起.这种沉积结构在以往的KMC方法模拟结果中从未出现.因此Stannard和Martin等[21]建立了耦合溶剂蒸发率的动态化学势函数用于研究双尺度沉积结构的形成机理.

上述利用KMC方法对纳米流体液膜蒸发沉积过程的研究均采用二维假定.而实际纳米流体液膜通常存在一定的厚度,因此应考虑蒸发沉积时不同层纳米流体化学势的分布和变化,以及纳米颗粒之间的相互作用.为此,近年来发展了基于不同厚度预测液膜蒸发的三维模型,并用于预测网状连续结构及枝状分形结构等沉积结构[23,27-29].对于Stannard等实验发现的纳米流体液膜蒸发沉积的双尺度结构,目前尚未见采用分层定义动态化学势的三维模型的研究报道.本文在Rabani等[16]提出的二维KMC模型的基础上建立了三维KMC模型,并将模型划分为多层结构,加入了耦合溶剂蒸发率的动态化学势函数[21],分别为三维模型的每一层液膜定义了不同的动态化学势,使之随着每层液膜溶剂蒸发率的变化而变化,更贴近于液膜真实蒸发情况,以此模拟纳米粒子的双尺度沉积结构,并讨论了化学势锐度与流体临界蒸发率对纳米流体液膜自然蒸发双尺度沉积结构的影响.

2 模型及化学势函数

2.1 模型及假定

本文建立的三维纳米流体液膜模型如图1所示.图中仿真区域边长为1024 × 1024个格子,红色格子代表纳米粒子,蓝色格子代表液体,绿色格子代表基板,所有模拟结果图尺寸均为1024 × 1024.本文建立的纳米流体液膜计算域是厚度为4层的纳米流体液膜层(根据计算能力和模拟需要,格子数和层数理论上可无限扩充),第一层为基板层,第二层为与下层基板和上层液膜接触的液膜底层,第三层为与上下两层液膜接触的液膜中间层,第四层为与下层液膜和上方空气接触的液膜顶层,纳米流体液膜的所有状态与变化都可由这四层表示.本文对三维纳米流体液膜的蒸发过程做出如下假设:

1)纳米流体液膜的厚度足够小,不考虑对流且忽略液膜的曲率变化,并假设纳米粒子在液膜内均匀分布;

2)干燥过程属于自然蒸发,液膜外部环境保持不变;

3)纳米流体液膜自然蒸发过程中粒子的移动主要由液体蒸发驱动[16,25].

基于以上假设,本文采用KMC模型对三维纳米流体液膜的蒸发与沉积过程进行模拟.

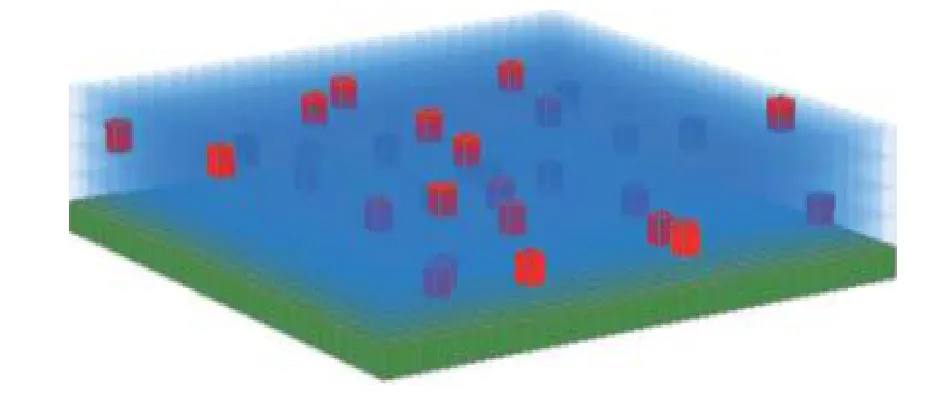
图1 纳米流体液膜的物理模型图Fig.1.Physical model of 3D nanofluid thin-film.

2.2 KMC模型

本文建立的三维KMC模型是由二维KMC模型发展而来[16],主要通过计算整个系统的能量变化来确定液膜中的液体是否蒸发、气体是否冷凝以及纳米粒子是否移动.在KMC模型的具体计算过程中,纳米粒子的具体尺寸对模拟结果的影响不大,并非关键参数[16],计算时假设一个纳米粒子占据一个格子; 模型中的基板体现为具有固体特性的1024 × 1024个格子,且与纳米粒子状态相同,不涉及基板具体材料对沉积结构的影响.模型中共存在三种不同的状态: 气态、液态、固态(基板和纳米粒子),而模型中的每一个格子只能存在一种状态.在此模型中采用三个相应参数,用以表现任意格子的状态: l,n,s.具体表示如下: l=0,n=0(气体); l=1,n=0 (液体); l=0,n=1 (纳米粒子); s表示基板.

计算开始后,首先将液体填充进计算域内的所有格子,然后根据模型预先设定的粒子浓度,将相应数量的纳米粒子随机地分布在由液体格子组成的液膜中,液膜四周边界采用封闭区域边界处理,即边界处状态与纳米粒子相同.开始蒙特卡罗计算时,每一次计算都包括三部分尝试: 首先尝试改变每一个液体格子的状态,使其状态变为气体,即蒸发过程; 然后尝试改变每一个气体格子的状态,使其状态变为液体,即冷凝过程; 最后进行N次尝试,使每一个纳米粒子朝着一个随机方向移动,N为粒子在液体中的扩散率.这里的每一次尝试是否成功都由Metropolis概率(Pacc)所决定[16]:

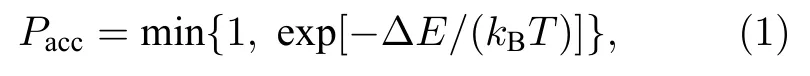
式中ΔE是格子状态改变前后系统哈密顿量(Hamiltonian)的变化值,kB是玻尔兹曼常数,T是温度,Pacc是模拟计算中每一次尝试是否成功的概率.将Pacc和系统随机生成的值进行比较,大于随机值则尝试成功,如果小于随机值则尝试失败,即格子状态不会改变,并开始下一次尝试.在模型中,由于粒子移动主要是由液体的蒸发推动,所以纳米粒子只能移动到液体格子区域,并与液体格子交换位置来保持溶剂密度不变.而当纳米粒子周围没有液体时,纳米粒子便无法移动.当计算域中没有液体时,则模拟结束.

模拟中采用的三维KMC模型通过计算整个系统的能量涨落来判断纳米流体中的蒸发、冷凝和粒子的移动.系统的总能量由哈密顿量(E)来表示[25],

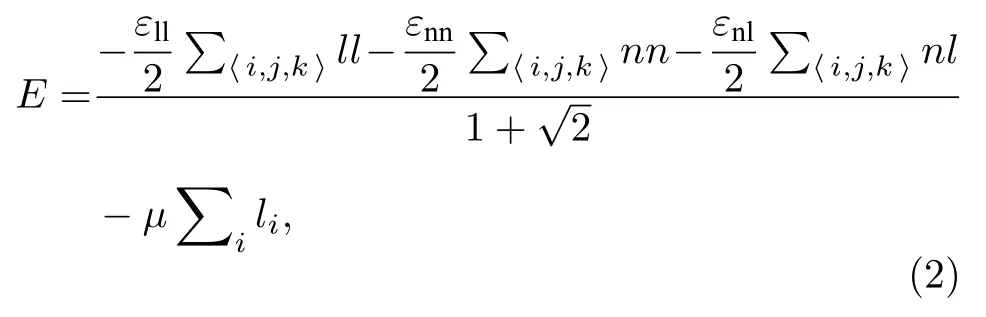
式中εnn,εnl,εll分别表示相邻纳米粒子之间的相互作用能、相邻纳米粒子和纯组分液体之间的相互作用能、相邻纯组分液体之间的相互作用能.在进行三维KMC方法计算时,将纳米粒子和基板之间的相互作用能和纳米粒子与纳米粒子之间的相互作用能大小取值一致.除此之外,所有的相互作用能都是纯组分液体相互作用能εll的倍数,在本文中定义 εnn=2εll,εnl=1.5εll,在整个模拟计算过程中,基板的状态始终恒定.如图2所示,在系统能量计算时,需要计算与中心计算点接触的6个一级接触点和12个二级接触点,由于有距离衰减,所以在计算二级接触点的作用力时要乘以加权值

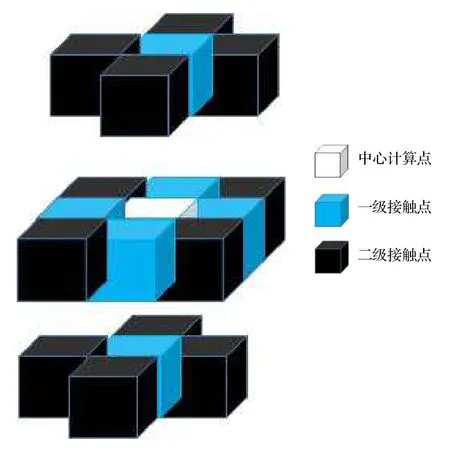
图2 接触点示意图Fig.2.Schematic diagram of contact points.

2.3 动态化学势函数

在KMC模型中,液体的蒸发主要由液体的化学势和系统的内能两部分决定[18].基于本文之前的假设,三维纳米流体液膜在蒸发过程保持恒温状态,其内部温度不会因为蒸发散热而改变,所以系统的内能在蒸发进行过程中保持恒定,因此在蒸发过程中液体的蒸发主要由系统的化学势决定.二维模型中封闭纳米流体液膜在化学势的处理上将其看作定值[11,14,16,20,22],所以沉积结构单一.本文所采用的化学势函数中耦合了溶剂蒸发率,使之成为了动态化学势,并分别为模型中的每一层液膜定义了不同的动态化学势,使之更贴近于液膜真实蒸发情况.动态化学势函数为[21]

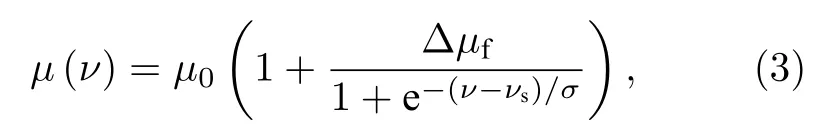
其中ν是溶剂蒸发率,νs是溶剂的临界蒸发率,μ0是系统的初始化学势,Δμf是化学势锐度,表示化学势突变的剧烈程度,变化幅度为初始化学势的相应倍数,σ是无量纲常数,本文取σ=0.01.由(3)式可知,化学势函数中间会发生一次突变,产生前后两个不同的化学势值,因此模拟前后会有两个不同的蒸发速率.本文将此动态化学势应用到三维模型中来预测纳米流体液膜自然蒸发形成的双尺度沉积结构.

2.4 模型验证

2.4.1 液膜各层蒸发状态

图3中的模型参数为: ∅=16%,kBT=0.20,μ0=—3.65,N=30,Δμf=0.15,νs=55%,σ=0.01,其表示的是纳米流体液膜在200—1000蒙特卡罗步数(MCS)时各层的蒸发状态,∅ 为纳米粒子浓度.图3(a)—(e)是顶层液膜,图3(f)—(j)是中间层液膜,图3(k)—(o)是底层液膜.如图所示,灰色区域为纯组分液体,黑色区域为纳米粒子,白色区域为蒸汽.在封闭边界的三维纳米流体液膜蒸发时,首先会随机在顶层蒸发成核,但并不是顶层完全蒸发干燥后才进行下面各层的蒸发,而是先蒸发形成孔洞,然后孔洞区域向四周和下方扩大,直到各层蒸发率达到临界蒸发率时各层的化学势分别发生突变,液膜内的液体迅速蒸发,纳米粒子则在基板层沉积,图3(c)和图3(d)便是顶层液膜化学势突变后液体迅速蒸发的结果.在蒸发过程中,上层的纳米粒子会随着液体的蒸发而下移,下层的纳米粒子则会随着上层的两相接触线的扩大而后退.随着上层流体的蒸发,纳米粒子会在下一层接触空气的两相接触线处聚集.因为每一层都有纳米粒子,所以沉积结构中三相线这部分为重合结构,重合的多少和纳米粒子的浓度有关.在图3(e)、图3(j)与图3(o)中可以看出,最上层和中间层的沉积附着在底层沉积结构上,形成最终的沉积结构,因此,本文后面的模拟结果均直接采用底层沉积结构表示.

图3 三维纳米流体液膜各层蒸发图Fig.3.Evaporation diagram of each layer of 3D nanofluid thin-film.

2.4.2 模拟与实验对比

图4是纳米流体液膜蒸发的实验与模拟对比图.图4(a)是厚度为80 nm的聚苯乙烯(polystyrene)液膜在硅基板上的干燥去湿实验过程[31],图4(b)是纳米粒子浓度 ∅=12%的纳米流体液膜蒸发干燥模拟过程,其中kBT=0.20,μ0=3.775,N=30,Δμf=0.15,νs=95%,σ=0.01.对比图4(a)与图4(b)可知模拟与实验过程一致,结果吻合良好,由此验证了本文模型的可靠性.

3 结果与讨论

3.1 双尺度结构模拟

图5(a)和图5(b)分别为采用动态化学势得到的双尺度细胞网络状沉积结构模拟结果和实验结果[21]的对比.图5(a)显示了使用动态化学势后液膜蒸发沉积的模拟结果,其中kBT=0.20,μ0=3.75,N=30,Δμf=0.15,νs=55%,σ=0.01,∅=12%,图5(b)是尺寸为2 nm的金纳米粒子与辛硫醇组成的浓度为1 mg/mL的纳米流体液膜干燥后5 μm2大小的原子显微镜(TM-AFM)图,模拟结果和实验结果之间的对应性很强.由图5(b)可知,图中的大尺度细胞网络结构占主导地位,而小尺度的沉积结构则出现在大尺度细胞网络之间.模拟开始时,在整个薄膜的随机位置发生慢热成核,薄膜中的孔随后逐渐生长形成大尺度细胞网络结构.然而,随着溶剂的蒸发率ν接近临界蒸发率νs,化学势μ会出现跳跃式增加,这时蒸发系统不稳定,会在极短的时间内在液膜剩下的液体区域中形成许多小孔,然后迅速干燥直至完全沉积,形成小尺度网状甚至是点状沉积结构,与大尺度细胞网络结构一起构成双尺度沉积结构.

图4 实验结果与模拟结果对比 (a)实验结果[31]; (b)模拟结果Fig.4.Comparison between experimental and simulation results: (a)Experimental results[31]; (b)simulation results.

图5 双尺度细胞网络结构模拟结果与实验结果对比(a)模拟结果; (b)实验结果[21]Fig.5.Comparison of simulation and experimental of dualscale cellular network structure: (a)Simulation result;(b)experimental result[21].

图6 双尺度纳米粒子环状结构模拟结果与实验结果对比 (a)模拟结果; (b)实验结果[21]Fig.6.Comparison of simulation and experimental of dualscale nano-rings structure: (a)Simulation result; (b)experimental result[21].

图6(a)和图6(b)分别是双尺度纳米粒子沉积环结构的模拟结果与实验结果[21]的对比.其中图6(a)模拟参数如下: kBT=0.22,μ0=3.60,N=30,Δμf=0.15,νs=0.09,σ=0.01,∅=15%; 图6(b)是大尺度纳米粒子沉积环结构与小尺度沉积结构共存的1 μm2TM-AFM图像,图像由尺寸为2 nm的金纳米粒子与辛硫醇组成的浓度为1 mg/mL的纳米流体液膜干燥后所得.对比图6(a)和图6(b)可以发现,模拟结果与实验结果吻合良好.从实验与模拟图中可以看出存在两种不同类型的沉积结构,这表明蒸发过程中存在两种不同的干燥模式,即化学势突变前的缓慢干燥模式与化学势突变后的迅速干燥模式.利用加入模型中的动态化学势可以成功地模拟这两种干燥模式.

3.2 化学势锐度对沉积结构的影响

图7是在不同化学势锐度下蒸发结束后三维纳米流体液膜的沉积结构,其中 ∅=12%,μ0=—3.75,kBT=0.20,N=30,νs=55%,σ=0.01.图7(a)—(f)的化学势锐度 Δμf分别为 0,0.050,0.100,0.125,0.150,0.200.在蒸发过程中溶剂蒸发率达到临界蒸发率之后,化学势会发生突变,突变后的化学势大小是由化学势的锐度大小决定的,化学势的锐度越大,化学势突变之后和原来的差别就越大,而前后化学势的差别大小决定了双尺度沉积结构的差别状况.从图7(a)—(c)中可以看出,在相同初始化学势时,化学势锐度在一定范围内会对突变之后的沉积结构产生影响.当化学势锐度为零时,化学势不会发生突变,沉积结构与使用恒定化学势时出现的单尺度沉积结构相同; 当化学势锐度较小时,大尺度网状沉积结构与密集的小尺度网状沉积结构共存; 随着化学势锐度的增大,大尺度沉积结构保持不变,而密集的小尺度网状结构进一步变小,变为点状沉积结构.从图7(d)—(f)中可以看出,当化学势锐度超过一定值时,化学势锐度对沉积结构的影响会逐渐变小,最终双尺度沉积结构保持不变.

图7 不同化学势锐度下封闭纳米流体液膜的沉积结构图 (a)Δμf=0; (b)Δμf=0.050; (c)Δμf=0.100; (d)Δμf=0.125; (e)Δμf=0.150; (f)Δμf=0.200Fig.7.Sedimentary pattern of nanofluid thin-film at different chemical potential sharpness: (a)Δμf=0; (b)Δμf=0.050; (c)Δμf=0.100; (d)Δμf=0.125; (e)Δμf=0.150; (f)Δμf=0.200.

3.3 流体临界蒸发率对沉积结构的影响

图8是在不同流体临界蒸发率下蒸发结束后三维纳米流体液膜的沉积结构,其中 ∅=12%,μ0=—3.75,kBT=0.20,N=30,Δμf=0.150,σ=0.01.图8(a)—(f)的流体临界蒸发率νs分别为1%,10%,30%,55%,80%,100%.在其他参数不变时,临界蒸发率主要决定两种沉积结构的面积占比.如图8(a)所示,当流体临界蒸发率较小时,化学势在蒸发初期就发生突变,突变后的化学势绝对值较大,导致液体迅速蒸发,纳米粒子会直接沉积在基板上形成线条状或点状沉积结构,所以图8(a)全是小尺度沉积结构.图8(b)、图8(c)与图8(d)分别是化学势在蒸发前期、中期与后期发生突变的结果,其中大尺度沉积结构逐渐增多,小尺度沉积结构则逐渐减少.由图8(e)与图8(f)可知,当临界蒸发率很大时,纳米粒子在化学势突变前有足够的时间随着三相线的移动而聚集在不同三相接触线的汇聚处,并沉积在基板上形成与采用恒定化学势时获得的单尺度网状沉积相同的结构.

图8 不同临界蒸发率下封闭纳米流体液膜的沉积结构图 (a)νs=1%; (b)νs=10%; (c)νs=30%; (d)νs=55%; (e)νs=80%;(f)νs=100%Fig.8.Sedimentary pattern of nanofluid thin-film at different critical evaporation rates: (a)νs=1%; (b)νs=10%; (c)νs=30%;(d)νs=55%; (e)νs=80%; (f)νs=100%.

4 结 论

1)在二维KMC模型的基础上建立了三维KMC模型,并加入了耦合溶剂蒸发率的动态化学势,成功模拟出了双尺度细胞网络沉积结构和双尺度纳米粒子环状沉积结构,模拟结果与实验研究的结果吻合良好.

2)化学势锐度是决定双尺度沉积结构的主要参数,锐度为零时,沉积结构表现为单尺度分布;随着化学势锐度的增加,沉积结构向双尺度分布演变.

3)流体临界蒸发率决定了双尺度沉积结构中两种不同沉积结构的面积占比,随着流体临界蒸发率的增大,小尺度沉积结构的占比逐渐减少,大尺度沉积结构的占比逐渐增加,直至全部变为大尺度沉积结构.