组合轮径差对地铁车辆动力学性能的影响*

(1.华东交通大学机电与车辆工程学院 江西南昌 330013； 2.西南交通大学牵引动力国家重点实验室 四川成都 610031)

由于车轮加工制造水平和精度的限制以及实际运行中轮轨摩擦磨耗的影响，铁道车辆各车轮的轮径不可避免地会存在一定程度的差异。而存在轮径差的轮对在运行过程中，为了保持左右车轮滚动圆半径相等，就会不可避免地向轮径较小的一侧产生横向移动，从而产生轮对横移，偏离轨道中心线，改变轮轨接触几何关系，进而会对车辆运行的稳定性和安全性等产生一定的影响[1-2]。此外，对于铁道车辆动力车辆，轮径差还容易引起由同一台牵引逆变器供电的并联电机的负荷分布不均，导致个别电机严重过载，从而使得动车产生空转或滑行现象[1-3]。

鉴于轮径差对铁道车辆的重要影响，相关专家对其开展了大量研究。池茂儒等[1]根据轮径差的大小将轮径差对车辆系统稳定性的影响划分为易稳定区、欠稳定区和亚稳定区，并分析了不同稳定区域内磨耗功率与动力学性能规律。池茂儒等[2]还研究了轮径差对安全性的影响趋势，并对比了转向架前后轮对同相轮径差与反相轮径差的影响程度。李润华等[4]对高速列车转向架中存在的初始轮径差进行了动力学仿真，并依据仿真结果研究了初始轮径差的限度制定标准。谷学思[5]分析了轮径差对高速动车组曲线通过性能的影响。李艳等人[6]针对实际运营线路中的某动车组,定期对车轮外形和轮径进行测量,研究分析踏面磨耗和轮径差变化对车辆运动稳定性和运行平稳性的影响趋势。

张志超等[7]基于正交试验方法基本思想，分析了六轴电力机车各轴之间的轮径差对曲线通过的影响。姚治锋和王勇[8]研究了轮对等值同相轮径差和等值反相轮径差对车辆临界速度的影响。韩鹏等人[9]对某高速线路服役动车组轮对型面进行跟踪测试,分析了磨耗型踏面与轮径差对滚动半径差函数形状与位置变化以及对动力学性能的影响规律。王晨等人[10]分析了不同轮径差值对地铁车辆磨耗的影响。

黄照伟等[11]分析了轮径差对轮对等效锥度的影响及对直线运行稳定性、运行平稳性和曲线通过性能的影响。刘思莹等[12]建立了机车动力学仿真模型和轮轨接触三维弹塑性有限元模型，分析了同轴轮径差对机车运行性能的影响。魏静和罗赟[13]研究了不同分布形式轮径差对某C0-C0三轴径向转向架机车曲线通过性能的影响。马卫华等[14]建立了某八轴重载机车牵引C80型运煤专用敞车列车模型，分析了机车在惰行和电制动工况下，轮径差对轮轨相互作用的影响。张云飞和李军[15]分析了不同轮径差形式对轨道客车在山区小半径曲线通过性能的影响。陈嵘等人[16]分析了高速车辆存在不同类型和幅值轮径差时通过道岔的稳定性、安全性和平稳性。

以上研究主要集中在对同一轴或同一转向架各轴左右两侧车轮存在轮径差时对机车性能的影响，而关于多种轮径差组合时对机车车辆动力学性能的研究还较少。而地铁车辆由于运行环境特殊，曲线半径普遍较小，且运行频繁，因此地铁车辆轮对很可能同时存在多种轮径差即组合轮径差，因此非常有必要对多种轮径差同时存在时对地铁车辆动力学性能的影响进行研究。

基于此，本文作者以某地铁车辆为分析对象，采用SIMPACK软件建立该地铁车辆的动力学模型，分析多种轮径差组合情况对地铁车辆稳定性、平稳性、安全性以及磨耗功率等方面的影响。

1 轮径差形式

1.1 轮径差形式

在理想情况下，转向架的4个车轮的轮径应该完全相等，但实际中由于各种因素的影响总是存在一定误差，在地铁车辆的实际运营过程中，轮径差的表现可由图1所示的4种典型形式组合得到。图1(a)中转向架前轮对有轮径差而后轮对无轮径差；图1(b)中转向架后轮对有轮径差而前轮对无轮径差；图1(c)中转向架前后轮对都有轮径差且同向；图1(d)中转向架前后轮对都有轮径差且反向。

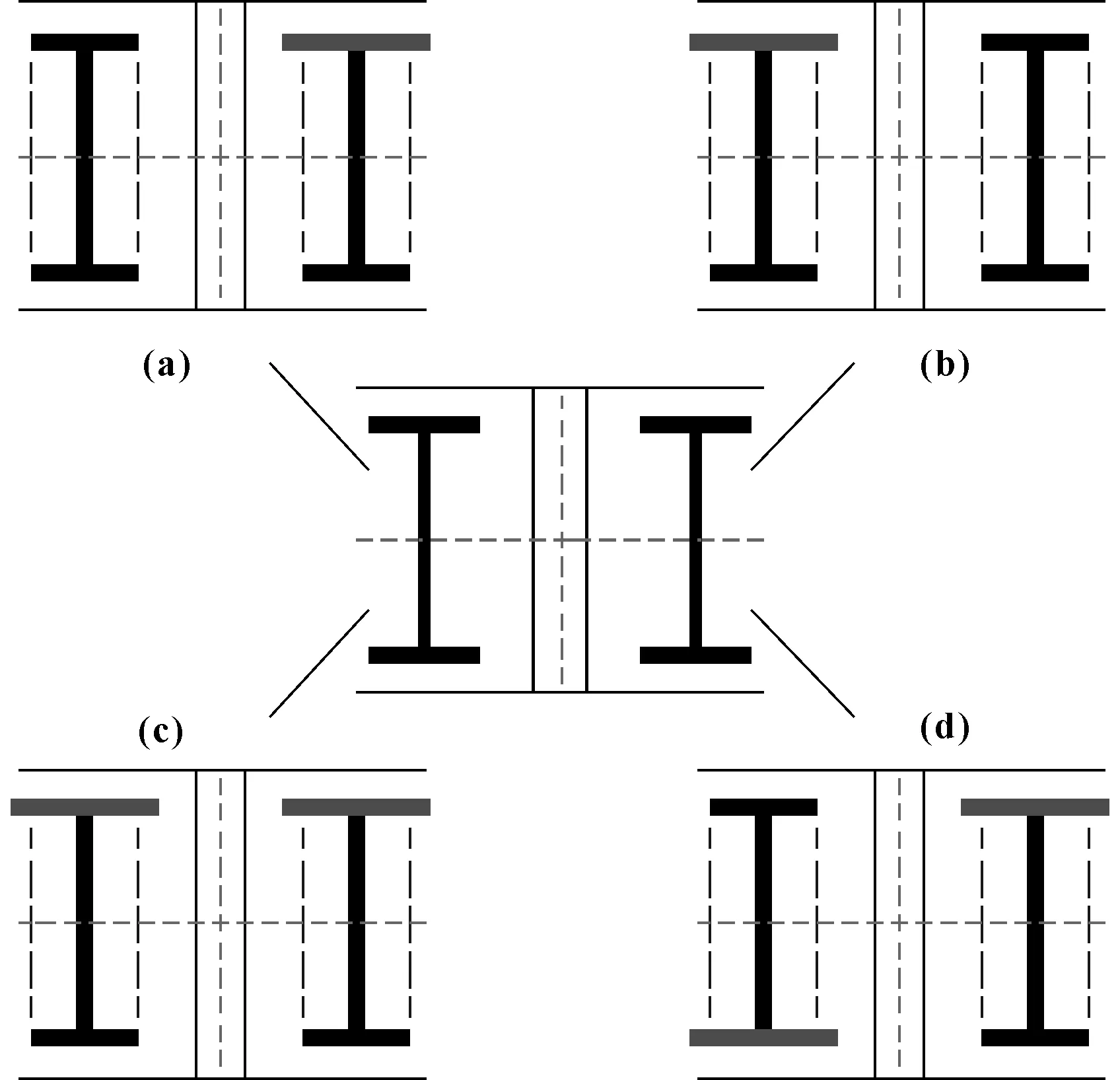
图1 轮径差形式Fig 1 Type of wheel radius difference

1.2 轮径差理论分析

以图1(a)为例进行分析，该转向架前轮对左轮的轮径大于其他车轮的轮径(其他车轮的轮径都为标准值且相等)，由于车轮与车轴采用过盈配合安装，所以具有相同的角速度，因此，轮径大的车轮线速度就会大于轮径小的车轮线速度。所以在运动过程中，前轮对左侧车轮拖拽右侧车轮向前运动，左侧车轮相对钢轨产生向前的蠕滑力，右侧车轮相对钢轨产生向后的蠕滑力，左右车轮受到的蠕滑力使轮对发生顺时针摇头运动，从而引起轮对向右侧横移[1]。

轮对的摇头和横移通过悬挂系统使构架也发生顺时针方向的摇头和横移运动，构架的摇头和横移又通过悬挂系统作用到转向架的二位轮对(即后轮对)，使后轮对也产生摇头和横移。但后轮对无轮径差，所以在运动过程中，后轮对右侧车轮滚动圆直径将大于左侧车轮滚动圆直径，根据前轮对的运动和受力分析可知，在此后运动过程中，后轮对的摇头角和横向位移将会减小，但并不会平衡于轨道中心线处。其他几种轮径差形式的分析方法与上述相类似，不再赘述[8]。

由上述分析可知，轮径差会改变轮对的对中平衡位置，进而改变轮轨接触关系，最终影响车辆系统的稳定性和安全性。而如果地铁车辆同时存在多种形式的轮径差组合，其受力必然会更加复杂，地铁车辆的运动也必将变得更加复杂，因此非常有必要对转向架同时存在多种轮径差组合时的动力学性能进行研究和分析。

2 动力学分析模型

2.1 地铁车辆动力学模型

以某地铁车辆为研究对象，基于多体系统动力学理论，采用SIMPACK动力学软件建立其动力学模型并进行多种轮径差组合工况下的动力学分析。该地铁车辆系统主要由车体、构架、轮对、驱动单元、牵引拉杆等质量体和弹簧、阻尼元件构成。该地铁车辆一系采用转臂式轴箱定位方式，并有轴箱顶置钢弹簧和一系垂向液压减振器，二系悬挂为空气弹簧、二系垂向液压减振器和一套横向减振器，二系还设有高度控制阀、差压阀以及非线性横向止档和Z字型牵引拉杆等。车辆模型的主要技术参数：轴距2 200 mm，轨距1 435 mm，车轮直径840 mm，采用LM型踏面，钢轨采用标准60 kg钢轨，最大运行速度80 km/h。其结构如图2所示。

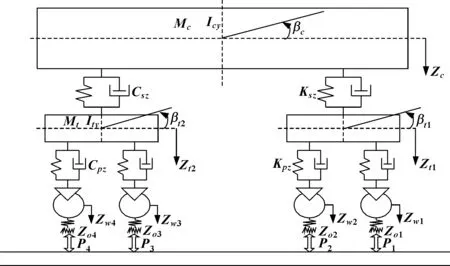
图2 地铁车辆结构示意图Fig 2 Metro vehicle structure schematic

该地铁车辆系统包括1个车体、2个构架、4个轮对、8个轴箱共15个刚体，车体、构架、轮对各取6个自由度，即伸缩、横移、浮沉、侧滚、点头、摇头；轴箱取1个绕轮对旋转的自由度，即点头自由度，整个车辆系统共50个自由度，独立自由度42个，垂向、横向运动耦合在一起。地铁车辆自由度如表1所示。

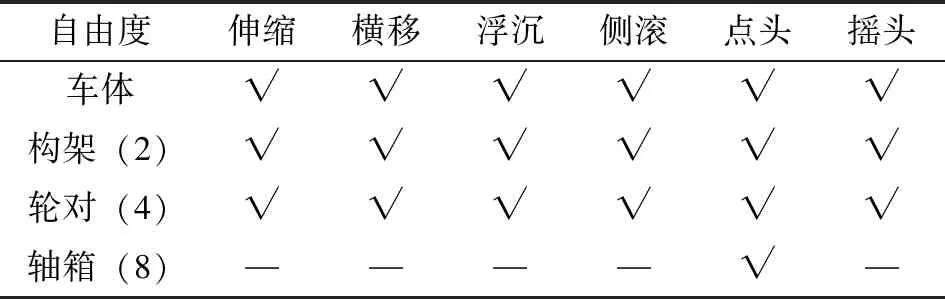
表1 地铁车辆自由度Table 1 Freedom of metro vehicle system

针对地铁车辆的多刚体系统，可列出各刚体运动微分方程的矩阵形式如下:

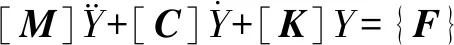
(1)

式中：[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；Y为广义位移；{F}为广义载荷。

在建模过程中考虑轮轨接触几何关系为非线性单点接触，轮轨间的蠕滑力由Kalker简化蠕滑理论(FASTSIM)进行计算，横向减振器、横向止挡等悬挂元件考虑为非线性力元。综合考虑以上因素，在SIMPACK软件中建立的地铁车辆非线性动力学模型如图3所示。

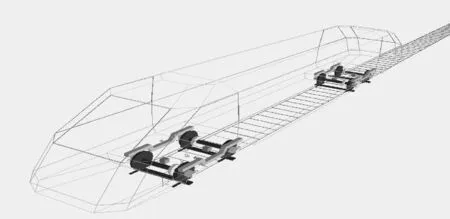
图3 地铁车辆非线性动力学模型Fig 3 Nonlinear dynamic model of metro vehicle

2.2 组合轮径差设置

文中计算模型轮径差定义为车轮与标准车轮在距轮对内侧70 mm处半径的差值。轮径差设置时遵循同一车轴左右轮径差为1～3 mm，同一个转向架前后两轴轮径差为3 mm，同一辆车轮径差为6 mm的原则。各轮直径设置如图4所示，各轮对初始轮径分别为846、843、843、840 mm，随后，1、3位轮对左轮和2、4位轮对右轮分部按图4所示数值变化(即同轴左右轮径差在变大)，每次轮径改变量为1 mm。

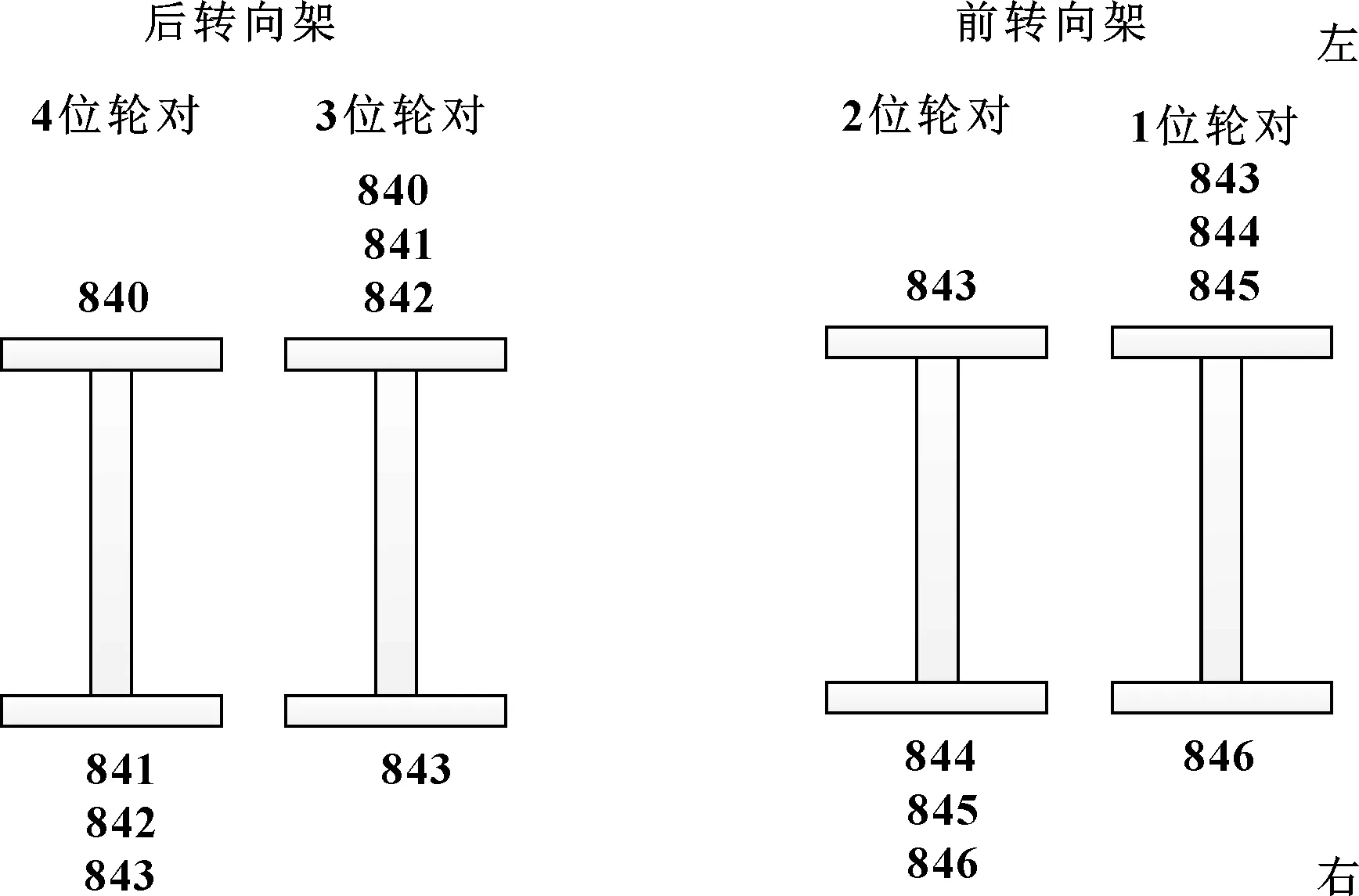
图4 地铁车辆组合轮径差设置Fig 4 Combination wheel radius difference setting of metro vehicle

3 轮径差对临界速度的影响

蛇行运动稳定性是车辆系统本身的固有属性[17]，地铁车辆在某一速度下运行稳定与否的评判依据是蛇行运动稳定性临界速度，简称临界速度。计算临界速度时，给定一段有限长的轨道谱激扰，让地铁车辆运行在不平顺轨道上并激发其振动，然后，让地铁车辆运行在理想光滑轨道上，观察轮对的横向振动能否衰减到平衡位置，来判断地铁车辆系统是否出现蛇行失稳。如在某一车速下轮对的振动不再收敛到平衡位置，则这时的车速值即为地铁车辆的实际临界速度。

计算结果如表2所示，可知，初始轮径差状态下地铁的临界速度为222 km/h，随着轮径差的增大，地铁车辆的临界速度逐渐减小，当同轴轮径差为3 mm时，临界速度仅为153 km/h，但是各轮径差下的临界速度仍然高于地铁车辆常规最大运营速度80 km/h，并且有较大的安全裕量。

表2 不同轮径差下的临界速度Table 2 Critical speed under different wheel radius difference

4 轮径差对平稳性的影响

地铁车辆的平稳性反映了旅客的乘坐舒适度，是衡量地铁车辆运行品质的重要依据。文中利用地铁车辆非线性动力学模型计算地铁车辆轮径差组合状态下的平稳性。计算平稳性时，车辆运行速度选为20～100 km/h，线路为直线轨道，轨道激励为美国五级谱，采用GB 5599-85标准进行评价。

地铁车辆平稳性计算结果如图5和图6所示。从图5可知，地铁车辆的横向平稳性随轮径差的增大而增大，当轮径差为0和1 mm时，在20～100 km/h运行速度范围内，车辆横向平稳性值均在GB 5599-85标准的“优”级限度值2.5以内；当轮径差为2 mm时，速度为80 km/h时，横向平稳性则很接近GB 5599-85标准的“优”级限度值2.5，平稳性恶化；当轮径差为3 mm时，速度为80 km/h时，横向平稳性则已经超过GB 5599-85标准的“优”级限度值2.5，平稳性进一步恶化。可见，在文中轮径差组合工况下，轮径差对地铁车辆的横向平稳性影响较大。从图6可知，轮径差变化对地铁车辆垂向平稳性影响不明显。

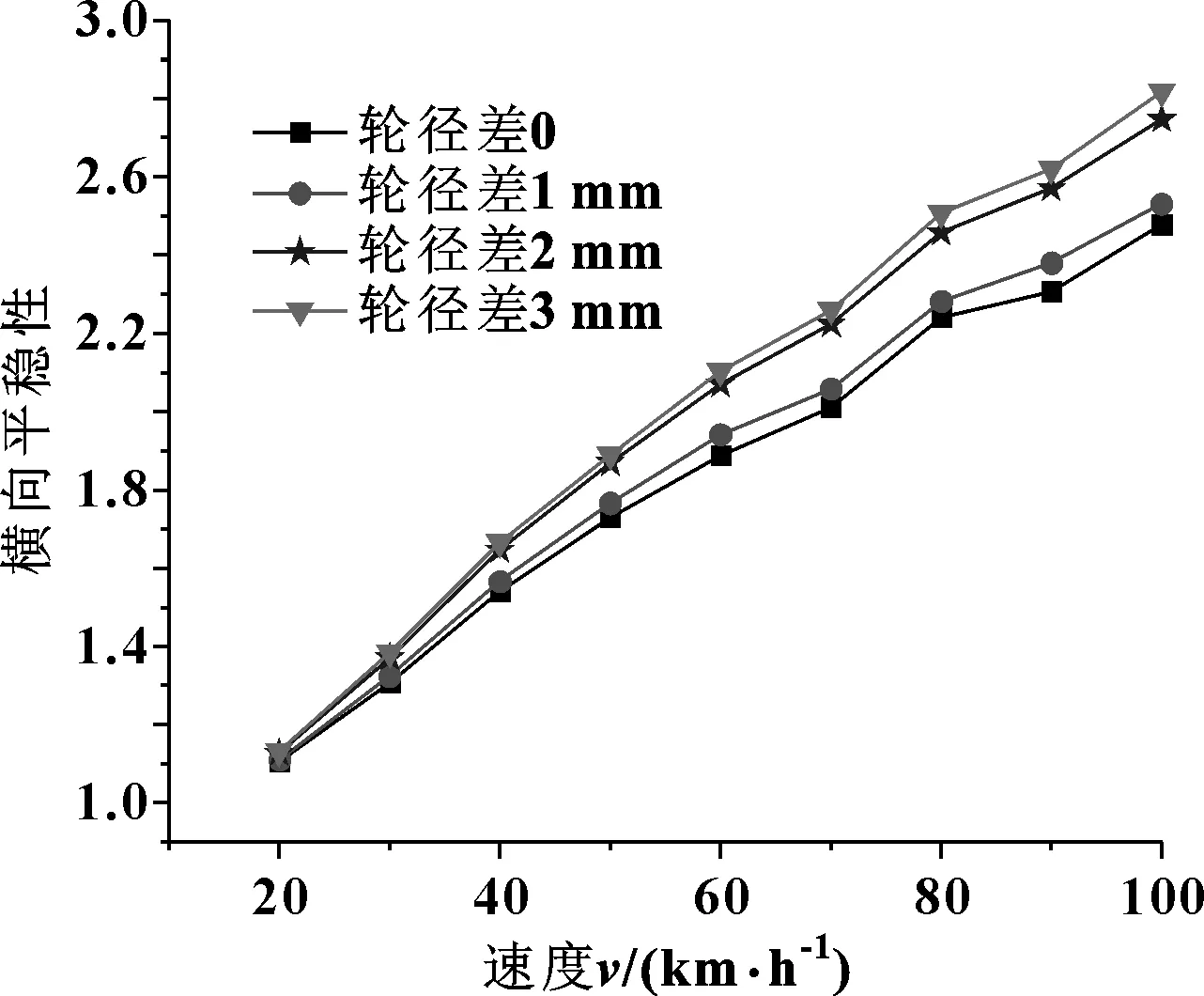
图5 不同轮径差时的横向平稳性Fig 5 Lateral Sperling value under different wheel radius difference

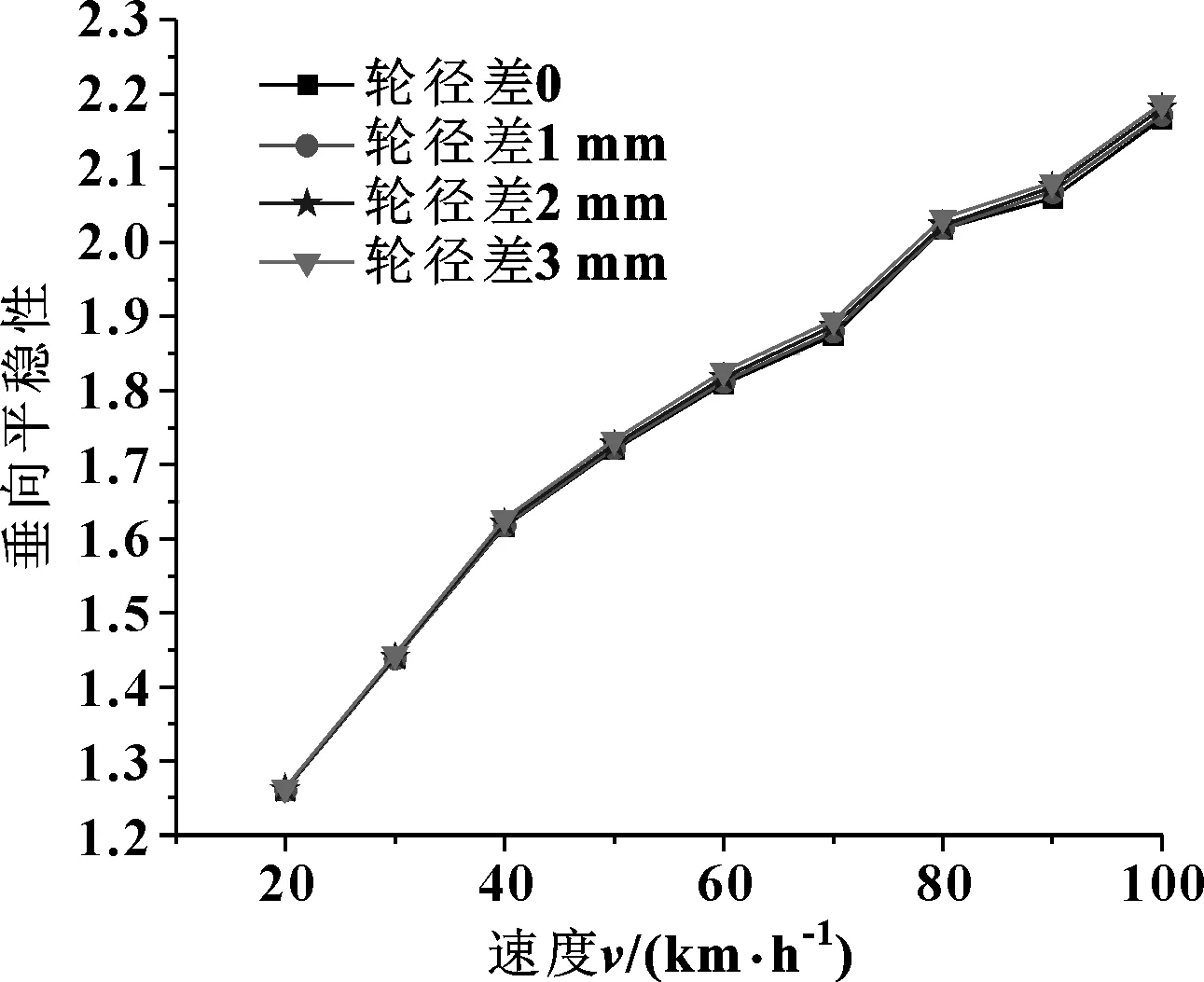
图6 不同轮径差时的垂向平稳性Fig 6 Vertical Sperling value under different wheel radius difference

5 轮径差对运行安全的影响

利用地铁车辆非线性动力学模型分析地铁车辆不同轮径差状态下的曲线通过性能。计算时采用美国五级谱轨道激励，曲线线路设置及速度如表3所示。采用GB 5599-85标准的轮轴横向力、轮轨垂向力、脱轨系数和轮重减载率这4个指标来评定车辆运行的安全性。

表3 曲线线路设置及运行速度Table 3 Curve line setting and running speed

5.1 横向力和垂向力

轮轴横向力和轮轨垂向力直接关系到列车曲线通过的安全性，是地铁车辆安全性的重要评价指标。轮径差组合工况下地铁车辆轮轴横向力和轮轨垂向力计算结果如图7和图8所示。可以看出，随着轮径差增大，轮轴横向力和轮轨垂向力变化不大，说明轮径差组合工况下轮径差对地铁车辆的横向力影响较小。

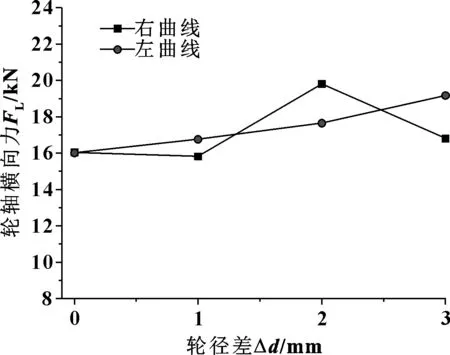
图7 不同轮径差时的轮轴横向力Fig 7 Lateral force of wheelset with different wheel radius difference

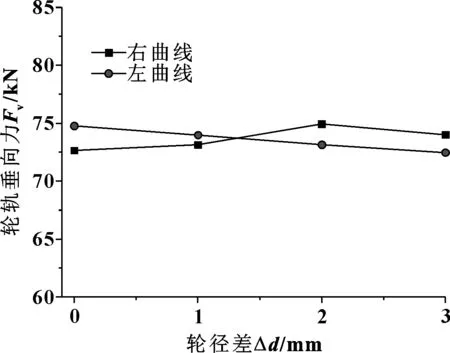
图8 不同轮径差时的轮轨垂向力Fig 8 Vertical force of wheel rail with different wheel radius difference

5.2 脱轨系数和轮重减载率

轮径差组合工况下地铁车辆脱轨系数计算结果如图9所示。可知，通过右曲线时，脱轨系数随着轮径差增大而略微增大；通过左曲线时，脱轨系数随着轮径差增大而略微减小；但脱轨系数指标都远小于GB 5599-85标准规定的限度值1.0，且有较大安全裕量。造成通过左、右曲线时脱轨系数影响差异的原因可能是文中组合轮径差中前后转向架、前后轮对及左右车轮都存在轮径差，因此在通过不同方向的曲线时，轮对横移量的不同造成了轮轴横向力影响规律的差异。

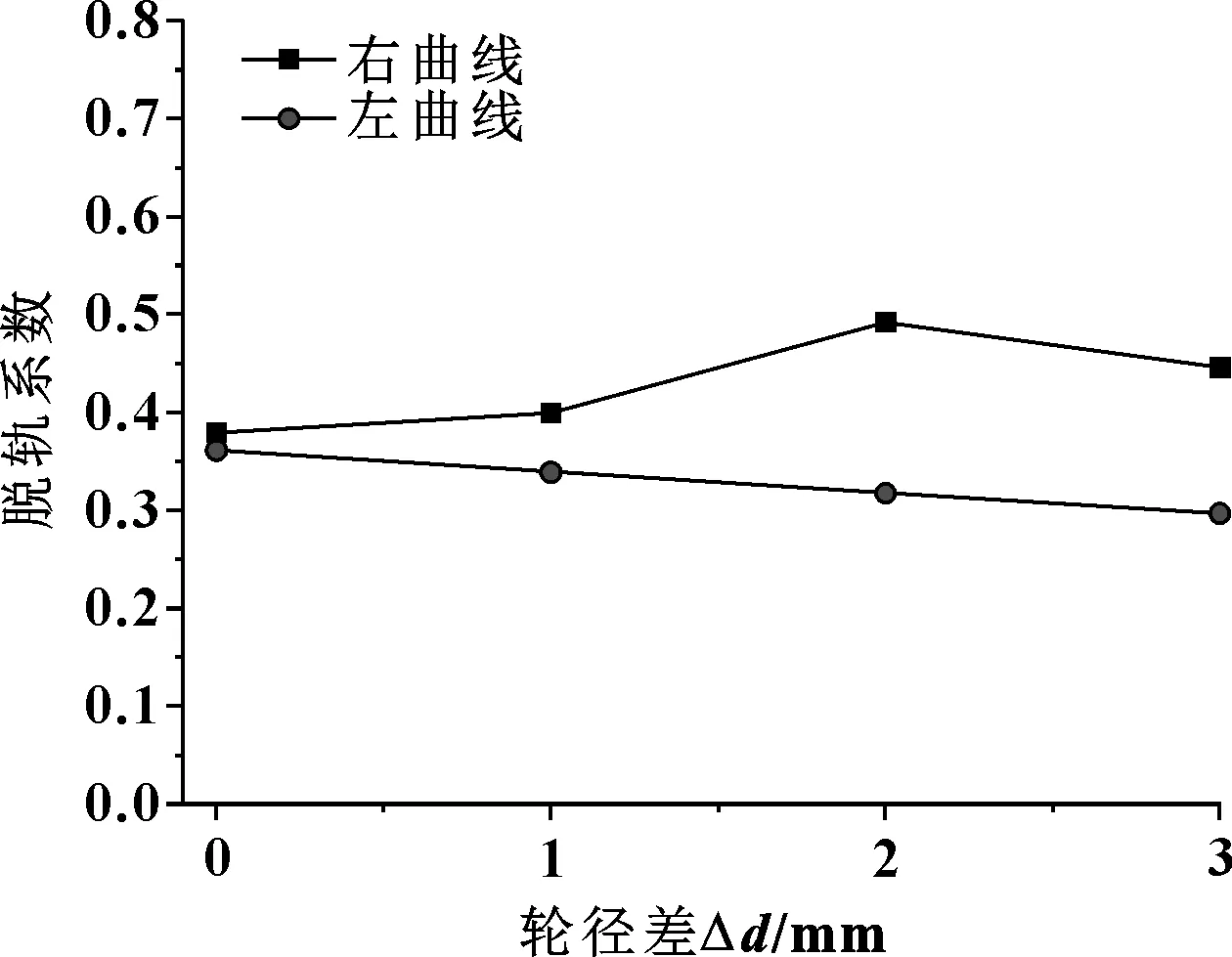
图9 不同轮径差时的脱轨系数Fig 9 Derailment coefficient under different wheel radius difference

轮径差组合工况下地铁车辆轮重减载率计算结果如图10所示，可以看出，轮重减载率受轮径差影响非常微小。

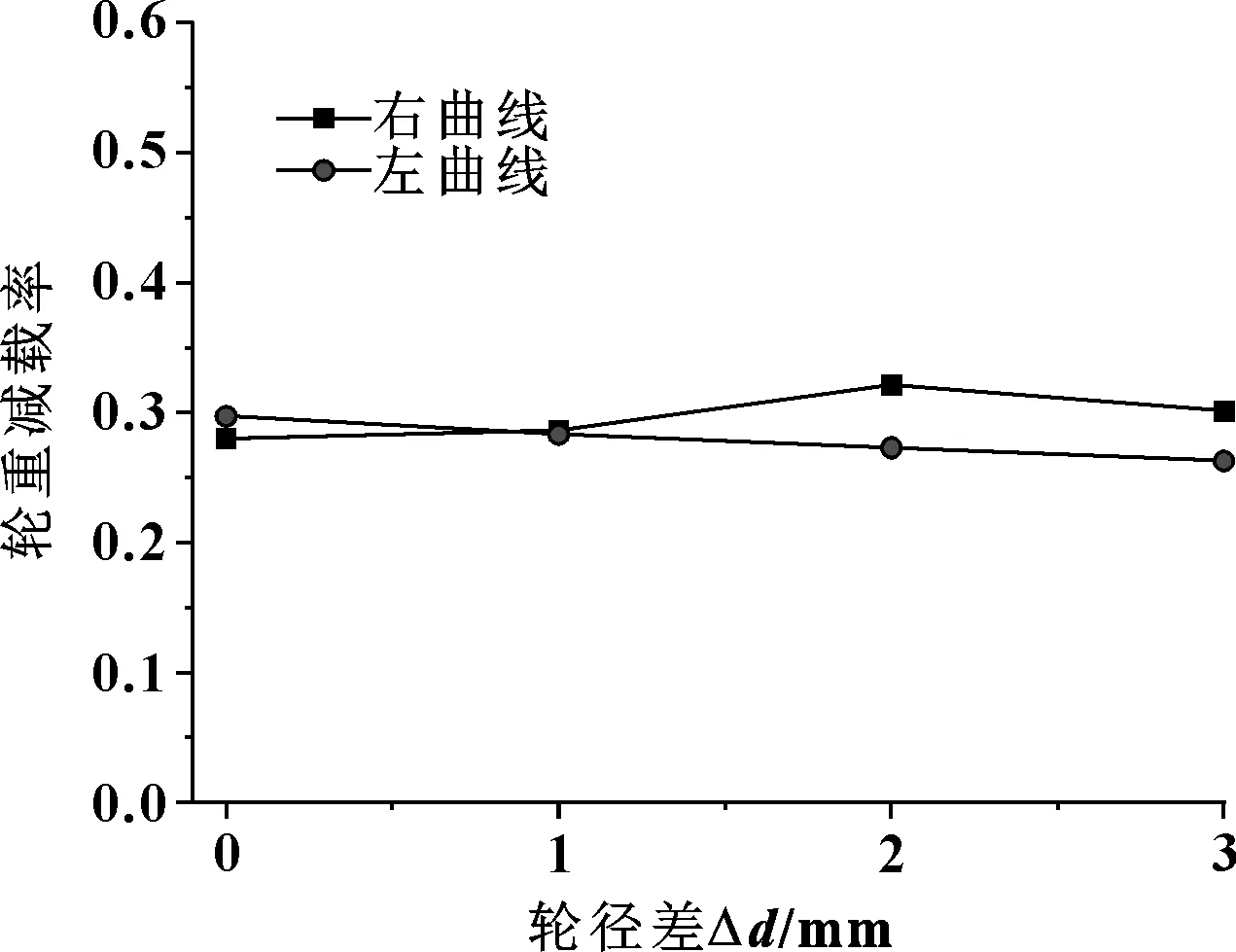
图10 不同轮径差时的轮重减载率Fig 10 Wheel unloading rate under different wheel radius difference

6 轮径差对磨耗功率的影响

轮径差组合工况下地铁车辆的磨耗功率计算结果如图11所示。

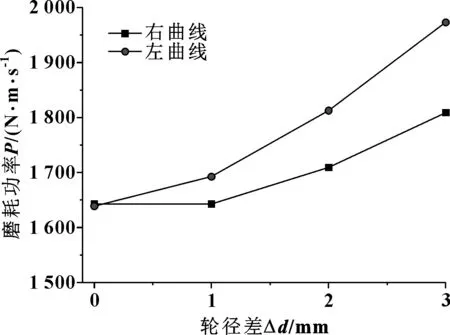
图11 不同轮径差时的磨耗功率Fig 11 Wear power under different wheel radius difference

由图11可知，磨耗功率随着轮径差增大而显著增大，说明轮径差对磨耗功率的影响较大，并且通过左曲线时的磨耗功率大于通过右曲线时的磨耗功率。当轮径差为0时，通过左、右曲线时磨耗功率差异为0.214%；当轮径差为1 mm时，差异为2.95%；当轮径差为2 mm时，差异为5.69%；当轮径差为3 mm时，差异为8.33%；但是总体增长趋势一致。通过左、右曲线时磨耗功率影响差异的原因可能是在组合轮径差中前后转向架、前后轮对及左右车轮都存在轮径差，因此在通过不同方向的曲线时，造成各轮对横移量差异较大，因此产生了磨耗功率变化的差异。

7 结论

(1)在轮径差组合工况下，轮径差的增大会使地铁车辆的临界速度有较大幅度降低，会使地铁车辆的横向平稳性和磨耗功率明显增大。

(2)在轮径差组合工况下，轮径差对地铁车辆的垂向平稳性、轮轴横向力、轮轨垂向力、脱轨系数和轮重减载率影响较小。

(3)通过左、右曲线时，轮径差对磨耗功率的增幅的影响存在差异，但是增长规律一致。