轴耦合道路模拟试验关键控制因素研究

陈禹，周德泉，刘建文，王新伟

（广州汽车集团股份有限公司汽车工程研究院，广东 广州 511434）

前言

道路模拟试验由于具有周期短、重复性好、不受天气影响、可长时间不间断试验等特点，在汽车研发领域已得到广泛运用。美、欧及日本等汽车工业强国在该领域的研究较为领先，国内也先后有田力军[1]、胡毓冬、周鋐[2][3]等人针对其系统结构及控制原理进行了深入研究。目前，对道路模拟领域的研究主要侧重于迭代控制策略、与试验场或用户关联及其与仿真分析的结合应用等方面，而针对其结果准确性的影响因素方面则少有涉及。

在道路模拟试验过程中，台架设备、控制系统和车辆组成复杂的非线性系统，试验结果受台架状态、软件参数、车辆状态及环境等方面影响。本文基于6 自由度轴耦合道路模拟试验系统（二十四通道），对道路模拟试验过程进行梳理，针对其中影响试验结果的关键因素展开研究。

1 道路模拟过程分析

道路模拟试验主要步骤包括：①道路载荷谱采集；②数据处理和编辑；③求解传递函数；④驱动谱迭代，获得驱动信号；⑤实施台架耐久。

1.1 道路载荷谱采集

道路载荷谱采集的目的是获取目标信号，采集通道包括控制通道和监控通道。控制通道用于台架迭代控制，一般为六分力、轴头加速度、悬架位移等；监控通道用于迭代结果辅助分析和判断，通常为塔座、质心加速度及底盘应变等。

1.2 数据处理

道路载荷谱采集获得的数据经去除异常幅值、除毛刺及去漂移等处理后，一般可得到至少5 组数据样本。道路模拟试验通常从中选择一组，经滤波、去均值、重采样等处理后作为目标信号。数据处理技术有系统理论和成熟软件的支持，而数据样本选取直接决定道路模拟目标信号，显得尤为重要。

1.3 求解传递函数及驱动谱迭代

通过白噪声激励进行系统识别，所得的频响函数矩阵即为系统传递函数H(jω)。对于该系统，输入和输出存在如下关系：

其中，X(jω)、Y(jω)分别为系统输入X(t)、输出Y(t)的傅里叶变换。根据RPC 理论，系统初始驱动信号由下式求得：

其中，X0(jω)为初始驱动信号X0(t)的傅里叶变换， Yd(jω)为目标信号Yd(t)的傅里叶变换，H-1(jω)为传递函数H(jω)的逆矩阵，g 为增益系数。

后续驱动信号求解公式为：

式中，Xi(jω)、Xi+1(jω)分别为第i 步、第i+1 步驱动信号的傅里叶变换，ΔX(jω)为驱动信号修正量，由Xi+1(jω)的傅里叶逆变换可求得下一步驱动的时域信号。迭代的一般流程如图1。

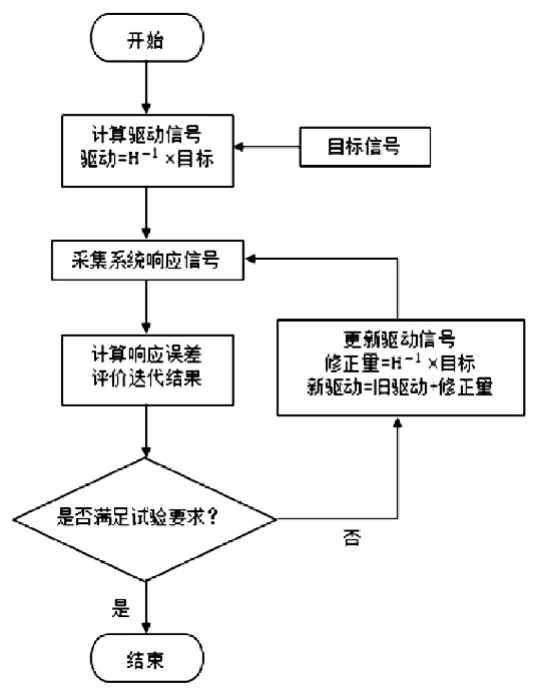
图1 迭代流程

传递函数求解以成熟的自动化控制理论为背景，结合台架设备特性，易形成固化的方法和流程；迭代过程由于非线性因素较多，对试验结果影响较大。

1.4 台架耐久

台架耐久是通过驱动信号重复以播放实现车辆耐久考核，过程中需要对减振器及底盘衬套进行充分冷却，并按时对车辆和设备进行点检。

基于上述分析，总结如下：

（1）目标信号作为道路模拟试验的输入条件和复现目标，选择合理与否非常重要；

（2）迭代结果直接决定道路模拟准确性，该过程中影响因素较多，主要包含车辆、台架系统以及环境（减振器、衬套冷却）等方面。

2 要素分析

综上，影响道路模拟试验的关键因素在于：①目标信号确定（样本选取）；②迭代控制参数，包括带宽、增益及迭代结果评价等；③车辆状态，如配重、减振器/衬套温度等。

2.1 目标信号确定

确定目标信号即选取存活率为50%的数据样本，按经验若有5 个样本，则有95%的概率使50%存活率的样本误差限度在5%以内，通常采用Rossow 方法[4]。

2.1.1 Rossow 方法原理

当子样较小时，无论抽样母体为何种分布，均可用以下方法来确定个体所对应的母体存活率估计量。

首先将所有样本进行排序，即：

则对应第i 个观测值Xi 的母体存活率P 为：

其中i 为样本排序号，n 为样本总数。

2.1.2 样本选取

载荷谱数据包含多个通道，因此不可能用式（4）和式（5）直接求算，需对各样本进行损伤向量模计算并归一化。以某车型载荷谱数据为例，首先对控制通道进行相对损伤计算，5个样本的计算结果见表1。

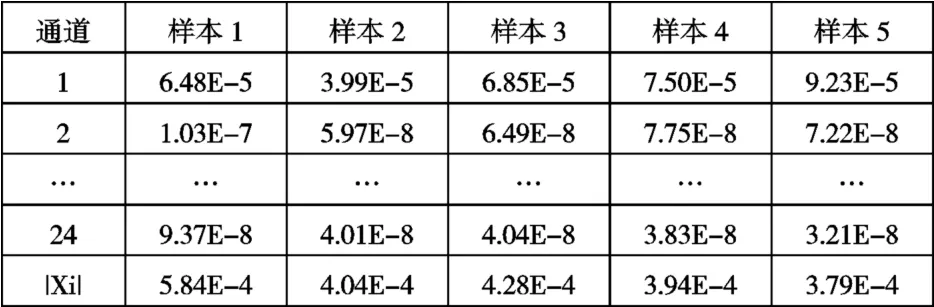
表1 样本损伤向量

以任一样本（如样本3）为基准将表1 结果归一化，结果见表2。

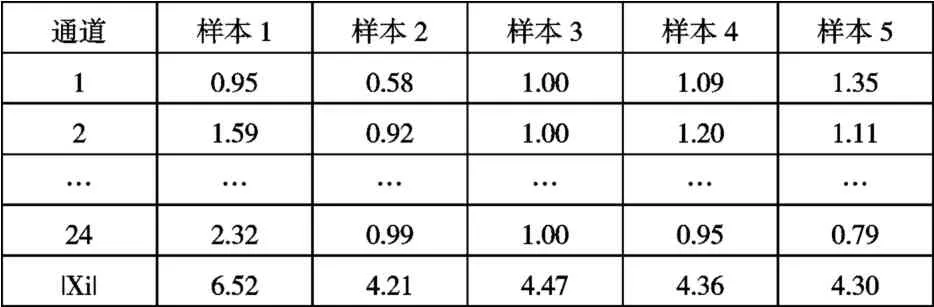
表2 归一化结果

根据式（4）和式（5）可得，样本4 即存活率为50%的样本。

2.2 迭代过程控制

2.2.1 控制带宽

根据频率分析结果，道路模拟迭代控制频率通常为0.6～50Hz，如图2 所示。

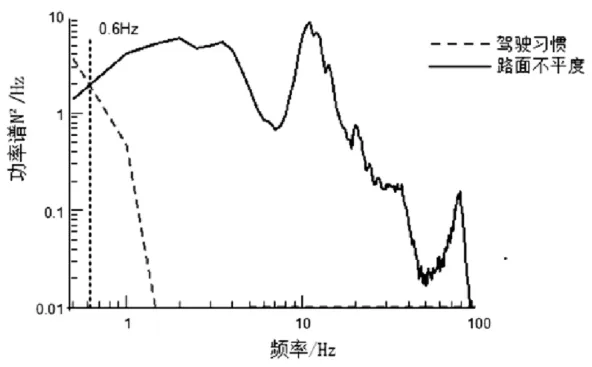
图2 道路载荷谱频率分析

为研究控制带宽对迭代的影响，针对某路面分别以0.6～50Hz、1～50Hz、2～50Hz、1～30Hz 等4 个频段进行迭代，直至所有控制通道RMS Error≤10%。迭代结果对比见图3。

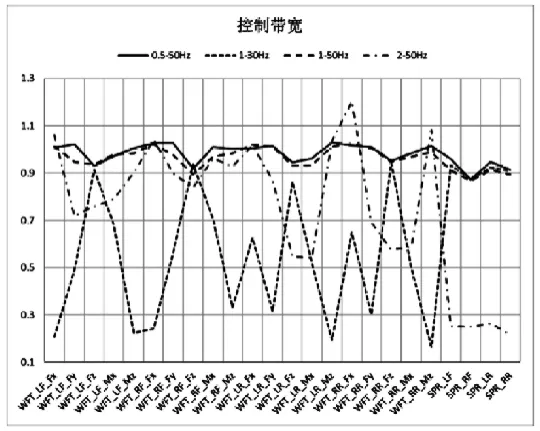
图3 控制带宽对迭代的影响

上图说明：

①以0.6～50Hz 和1～50Hz 迭代，均能获得理想效果，但前者存在响应超出目标的风险；

②以1～30Hz 迭代，高频成分损失较多，导致与轴头关联的载荷减小，但对车身响应无影响；

③以2～50Hz 迭代，车身姿态变化受较大影响，底盘响应无显著影响。

2.2.2 增益系数

针对某路面以1～50Hz 为带宽，取大、小两组增益进行迭代，直至所有控制通道RMS Error≤10%，对比Fx、Fy 及Fz 收敛曲线，结果见表3。

不难看出，较大的增益使收敛加快，提高迭代效率，但收敛曲线稳定性变差。尤其对于Fy，大增益使其发散风险更高。

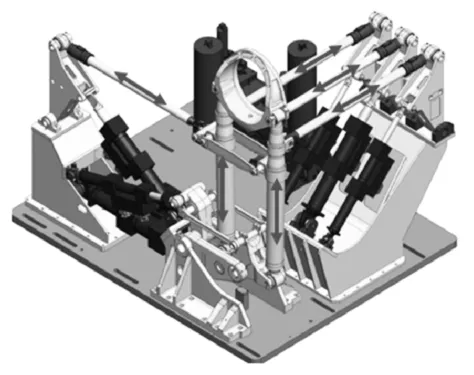
图4 二十四通道台架结构

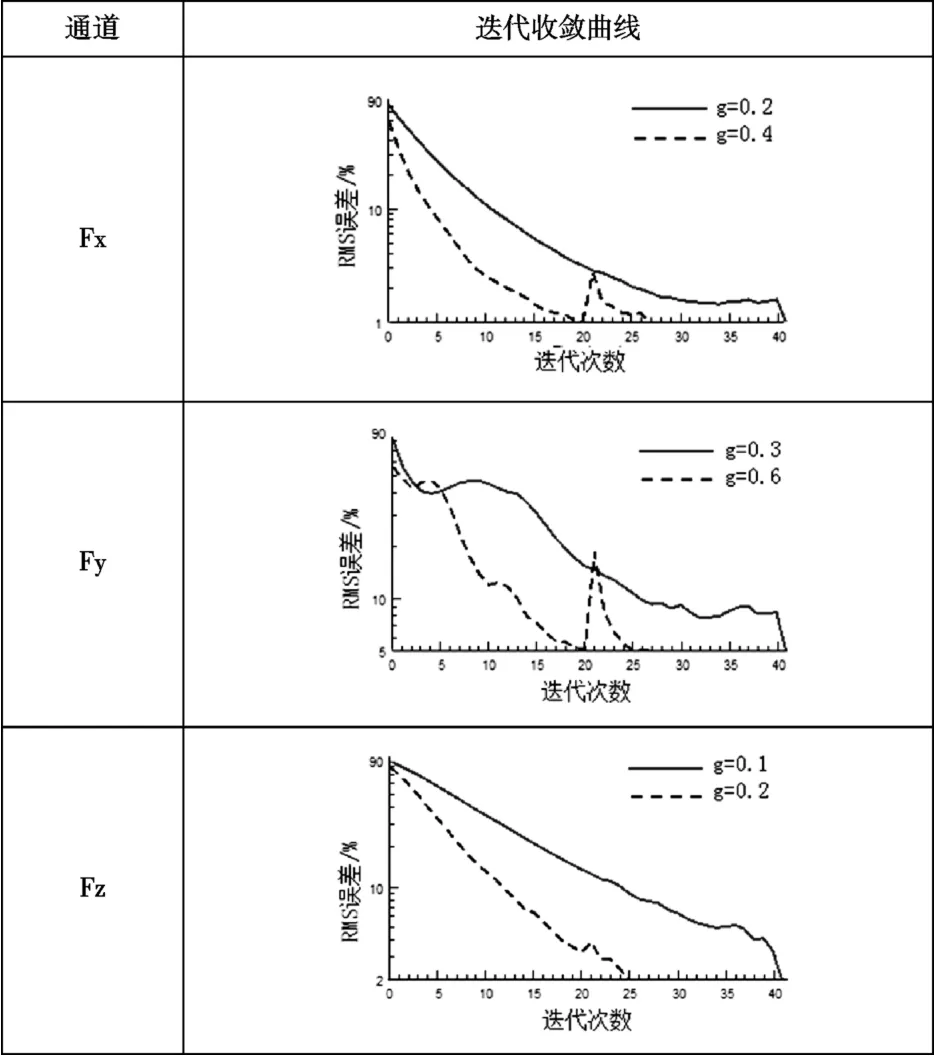
表3 不同增益系数收敛曲线

结合二十四通道台架结构特征，其纵向相对独立，而侧向和垂向互相干扰，如图4。现针对Fy 和Fz 进行大小增益控制下的收敛曲线对比，结果见表4。

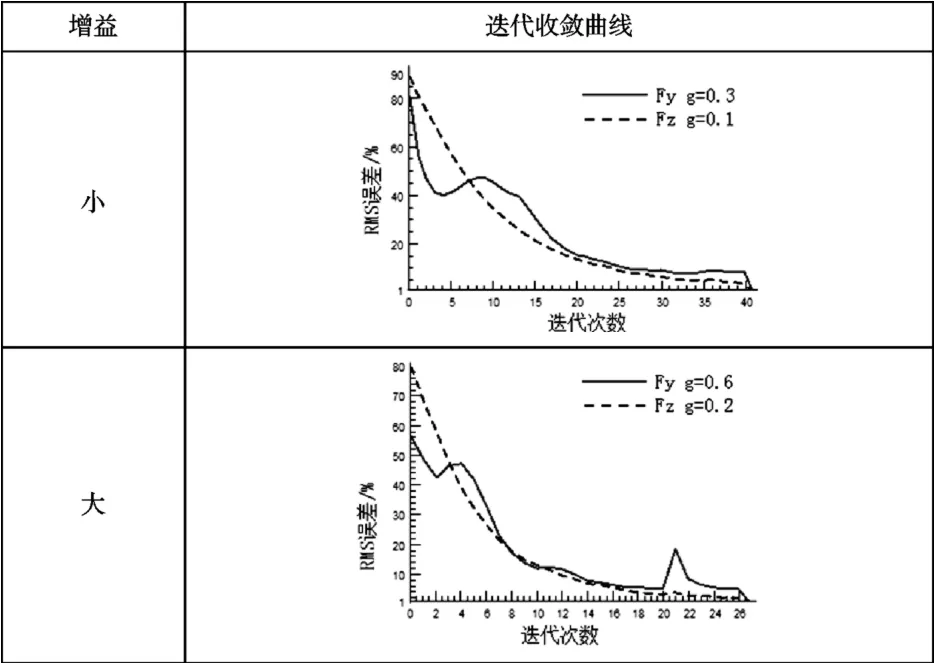
表4 不同增益系数下Fy、Fz 收敛曲线

可见Fz 增益变化对Fy 影响明显，其增益设置过大，易导致Fy 发散失控，应在开始时设置较小增益值，待Fy 趋于收敛后视情况调整各通道增益以提高迭代速度。

2.2.3 迭代结果评价

图5 试验场特征路面分类

如图5，试验场特征路面一般包含宽频随机型、特定频率型和瞬态冲击型3 种。对于前两种，结合RMS Error（均方根误差）、Response Max（最大值误差）和Response Min（最小值误差）三个指标，一般都易于实现较高的迭代精度。

考虑冲击型路面的迭代相对复杂，现以石块路和坑洼路两种类型路面的迭代结果进行对比，结果见表5。

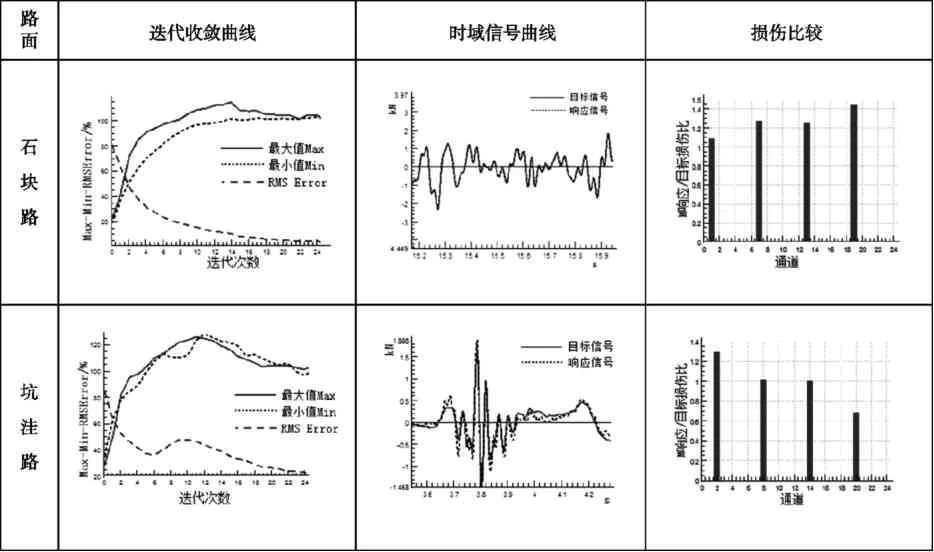
表5 不同路面迭代结果对比

坑洼路RMS Error 降至20%后趋于平缓，最大值、最小值吻合度均已接近100%。因此，对于冲击路面迭代结果的评价应侧重于最大值、最小值的复现度。

2.3 车辆配载

车辆配载对迭代响应有着直接影响，为实现最大化验证效果，选取满载、半载、空载三种状态进行研究，对比3 种载荷下的响应，结果见图6。

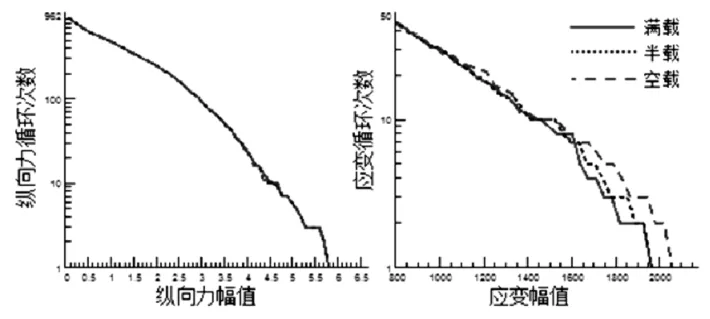
图6 不同载荷的雨流结果

图6 说明配载变化对六分力响应基本无影响，但车身运动(起伏、俯仰、侧倾等)随配载减小而变大。对比三种载荷状态下响应与目标的损伤比，六分力信号均可实现对目标的良好复现，但悬架位移损伤随配载减小而增大，空载状态下损伤比最大达1.7 倍，如图7 所示。因此，随着载荷减小，车身会产生额外运动，导致车身姿态偏差，并进一步导致车身相关零件的受力情况差异。

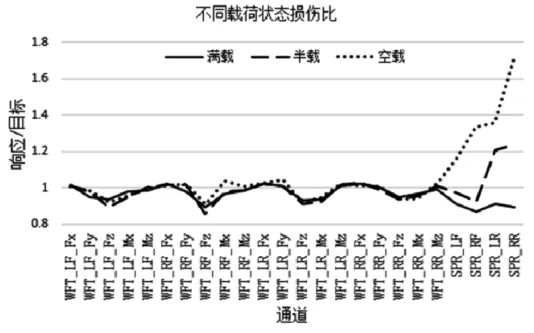
图7 不同载荷损伤分析结果

2.4 减振器温度

为研究减振器温度对车辆载荷的影响，以同样的驱动信号，分别在减振器为室温(26℃)和高温(90℃)时播放，对响应信号进行雨流分析，如下图。

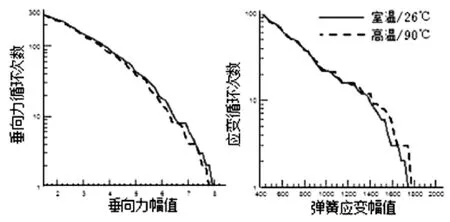
图8 不同温度的雨流结果

可见减震器温度升高后，阻尼力减小，悬架位移量增加，车身姿态变化更明显。同时，六分力损伤随减振器温度升高而减小，如图9 所示。响应与目标出现偏差，迭代控制受到影响。

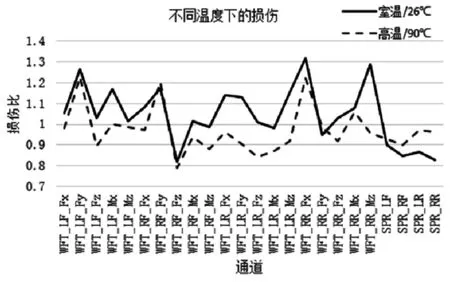
图9 不同减振器温度的损伤分析

此外，减振器温度升高导致悬架位移损伤增大，车身运动更明显，姿态控制更加困难。综上，减震器温度变化导致底盘和车身响应改变，迭代时为保证迭代效果和效率，应控制减震器温度处于合理范围，不发生明显变化。在耐久过程中也应注重减震器温度控制，以避免持续运动过程中温度上升，车辆受力与实际道路差异，导致道路模拟试验结果出现偏差。

3 总结

本文基于6 自由度轴耦合道路模拟试验系统，对道路模拟试验过程进行梳理，并针对试验过程中关键的影响因素展开研究，获得以下结论：

（1）控制带宽方面，与轴头响应强关联的零部件对上限频率较为敏感，而车身姿态相关零部件对于下限频率较敏感，迭代时应根据不同路面视情况选择合适的区间。

（2）侧向对于垂向的增益值变化非常敏感，迭代开始时应设置较小的垂向增益值，避免侧向发散。

（3）迭代结果应结合RMS 误差、最大值和最小值三大指标进行综合评价；对于冲击型特征路面，侧重于评估最大值和最小值的复现度。

（4）配重主要影响车身受力及姿态变化，而减震器温度变化则对底盘结构和车身运动均有影响，在道路模拟过程中应注重对其进行合理的温度控制。