基于线性插值法的年径流总量控制率与设计降雨量快速估算
刘 慧,孙 波,曾凡勇,谢水波
(1.南华大学建筑学院,湖南 衡阳 421001;2.南华大学土木工程学院,湖南 衡阳 421001)
年径流总量管控率与设计降水量是规划设计者编制海绵城市专项规划时必备的基础数据之一,查询相关规范与资料可直接获得各城市5%步长的年径流总量管控率与设计降水量,但除此之外更为精细的数据不仅少有文献记载,且重新计算的难度较大。我国海绵城市建设至今尚处于试点阶段,各单位也同样处在不断学习和探索时期,如何快捷、准确地求得某座城市5%步长以下的年径流总量管控率与设计降水量以用于海绵城市专项规划编制,是规划设计者所面临的难点。目前虽有不少学者做过相关科研探索,如史红波等[1- 4],但较少从本研究的切入点进行研究。因此,本研究就如何快速且较准确地计算出城市5%步长以下年径流总量管控率与设计降水量展开深入探索。
1 计算方法
1.1 统计法
《海绵城市建设技术指南——低影响开发雨水系统构建(试行)》(以下简称《指南》)在其附录2中阐述了设计降水量与年径流总量管控率的具体推算方法[5- 6]如图1所示,将本市近30年以上日值降水数据由小至大排列并删除小于及等于2mm的降水量,计算小于其中某一个设计降雨量的降水总量(小于此设计降水量的雨量值按照其实际值累加得出降水总量,而大于此降水量的则以此降雨量为最大上限累加出降水总量,二者相加得到的总和)在其总降水量中的占比,此占比即为年径流总量管控率[7- 9]。各省在编制《海绵城市建设技术导则(试行)》(以下简称《导则》)时,根据降水数据以5%为步长计算了各城市年径流总量管控率15%,20%,25%,…,90%,95%对应的设计降水量,用以指导当地海绵城市建设与专项规划修编。

图1 《指南》统计法
1.2 存在的问题
实践中,5%步长年径流总量管控率与设计降水量并不能完全满足海绵城市专项规划编制及相关科研工作的需求[10- 15]。以萍乡市莲花县年径流总量管控率75%、80%对应的设计降水量分别为22.5、26.7mm为例,若对某地块进行现状年径流总量管控率评估求得地块可控制的降水量为25mm,则无法通过查询江西省《导则》确定其对应的年径流总量管控率。只有应用《指南》中的统计方法再次计算设计降水量25mm对应的年径流总量管控率,然而这对于绝大多数规划设计者及普通学者而言存在一定难度。
1.2.1城市近30年日值降雨数据不易获取
国家气象信息中心网有《中国地面气候资料日值数据集(V3.0)》提供,其中包含1951年以来我国699个基本、基准气象站所有的日值气象资料,如气压气温、降雨量、雨水蒸发量、风向风速等数据,但仅限拥有省、部级以上相关领域科研项目的教育科研实名用户下载,并且699个气象站也仅包含中国一部分城市的气象数据。个人实名及单位实名用户可获得《中国地面累年值日值数据集(1981—2010年)》,但此数据集中的30年降雨数据为累年平均日值数据无法用于计算与统计。
1.2.2统计近30年日值降雨数据工作量大
获取降雨数据后需对数据进行整理计算,然而一座城市近30年的日值降水数据高达上万条,即使在EXCEL的帮助下也需要耗费相当多的时间才能得出各设计降水量对应的年径流总量管控率。在目前我国规划设计院大多比较注重投入与产出比的大背景下,根据万余条降水数据重新推求5%步长以下的年径流总量管控率与设计降水量其可实施性不强,且易出现为提高工作效率降低工作量而依照设计降水量数值区间对年径流总量管控率进行主观粗略赋值的现象。
因此,探索一种快速、简便、准确率高且无需重新统计本市近30年日值降雨数据的方法推求5%步长以下的年径流总量管控率与设计降水量对于海绵城市专项规划的深化及相关科研工作的推动具有一定的积极作用。
2 线性插值法探讨
2.1 线性插值法简介
为了探索函数的扰动规律,常常需要将不在表中的函数值求出,由此,通过已知的函数表制作一个不仅可以反映原函数F(X)特性,还便于推算的简化函数P(X),用P(X)替代F(X)并使P(Xi)=F(Xi)对i=1,2,3,…,n成立,如图2所示,其中P(X)就是人们制作的插值函数,此过程也被称作线性插值法。线性插值法即一种已知直线中两个端点的量用于计算两个端点之间某个未知量的函数方法,因可保证在节点上的插值准确率为100%且比抛物线插值等其他插值方法更为简便,所以在天文学、图形学、数学等领域被广泛采用。线性插值法常被用于代替原函数,也常用于推算符合函数规律的表格中没有列举的数值。
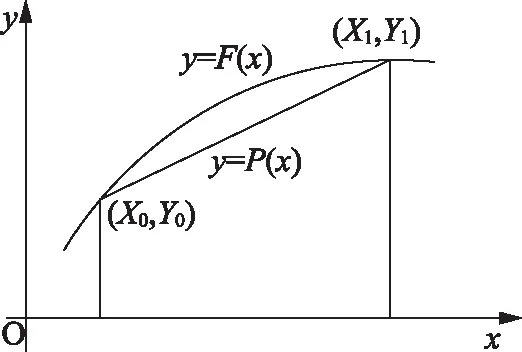
图2 线性插值法
假设图2中(X0,Y0)及(X1,Y1)两点为已知量,需要求出两点之间在直线上的某个未知量(X,Y),其线性插值法的直线方程可表达为:
(1)
式中,X0,X1,Y0,Y1—已知量;X—X0与X1之间任意的插值;Y—Y0与Y1之间任意的插值。
2.2 线性插值法估算案例
以萍乡市莲花县设计降水量与年径流总量管控率为研究对象,应用线性插值法推求其5%步长以下年径流总量管控率与设计降水量。根据江西省《导则》附录10.1获得萍乡市莲花县5%步长的年径流总量管控率与设计降水量取值表,见表1。
根据图2及式(1),可得到5%步长以下的年径流总量管控率推算公式:
(2)
式中,Y0—上一级的年径流总量管控率;Y1—下一级的年径流总量管控率;Y—待推算的实际年径流总量管控率;;X0—上一级的设计降水量;X1—下一级的设计降水量,X—容积法计算得出的实际设计降水量。
以萍乡市莲花县某地块实际可控制的降水量为25mm为例,由表1可知其上一级年径流总量管控率为75%,下一级年径流总量管控率为80%;其上一级的设计降水量为22.5mm,下一级的设计降水量为26.7mm。由此,将式(2)写为:5%步长以下的年径流总量管控率=75%+(25-22.5)×(80%-75%)/(26.7-22.5)。

表1 莲花县5%步长年径流总量管控率与设计降水量取值表(1987—2016年)
同时,可借助EXCEL动态计算功能实现5%步长以下的年径流总量管控率快速推算,见表2,在表格中的B3输入“=B2+(C3-C2)×(B4-B2)/(C4-C2)”键入回车后即可迅速获得结果。

表2 年径流总量管控率的快速估算
在特定情况下,若已知某个年径流总量管控率需要求出对应的设计降水量则可将式(2)逆推,得到其在EXCEL中的表达式“=(B3-B2)×(C4-C2)/(B4-B2)+C2”。将表达式输入表格中的C3后键入回车即可迅速求出结果,见表3。同理可计算出5%步长以下所有步长年径流总量管控率与设计降水量数据,篇幅所限仅给出1%步长的部分成果,见表4。若需要0.5%或更小的步长可应用上述方法求得。
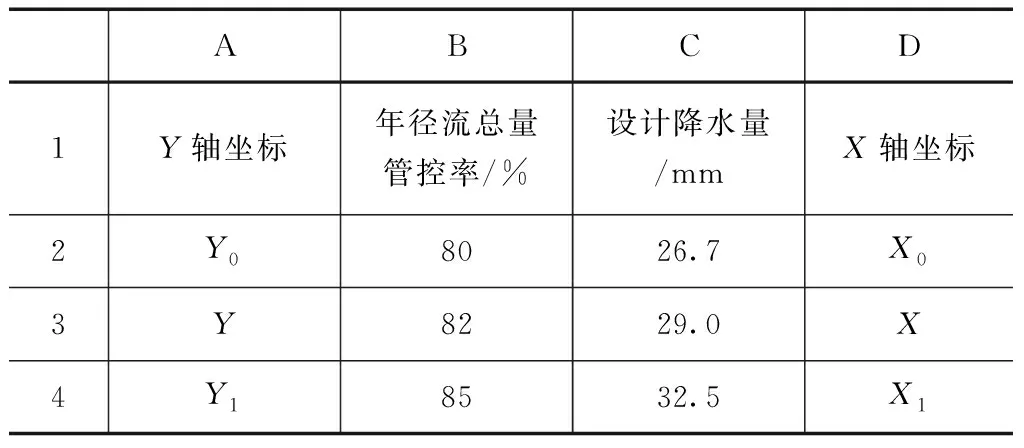
表3 设计降水量的快速估算

表4 莲花县1%步长年径流总量管控率与设计降水量估算表
2.3 误差分析
为验证线性插值法的可行性,需对线性插值法计算出的估算值与实际值做误差分析。因此,按照计算方法根据萍乡市莲花县1987—2016年10958条逐日降雨数据统计得出当地的实际年径流总量管控率与设计降水量,并将实际值与线性插值法的估算值进行误差分析,如图3所示。
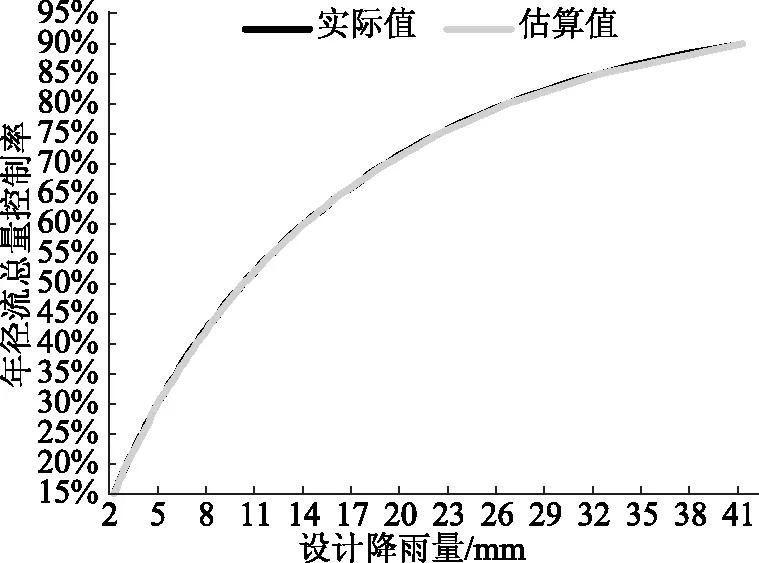
图3 年径流总量管控率误差分析
年径流总量管控率15%~40%区间中,设计降水量4.3mm对应的年径流总量管控率估算值与实际值偏差最大,分别为26%与26.52%,差值0.52%;年径流总量管控率40%~65%区间中,设计降水量7.7mm对应的年径流总量管控率估算值与实际值偏差最大,分别为41%与41.38%,差值0.38%;年径流总量管控率65%~90%区间中,设计降水量37.8mm对应的年径流总量管控率估算值与实际值偏差最大,分别为88%与88.37%,差值0.37%;综上所述,线性插值法估算萍乡市莲花县1%步长年径流总量管控率与设计降水量的最大误差值为0.52%,平均误差值为0.16%,区间中最小误差值为0%。误差分析结果表明线性插值法的估算准确率高。
3 结语
本研究基于线性插值法对莲花县年径流总量管控率与设计降水量进行了快速估算。虽然线性插值法具有着一定程度的局限性,但同时也具有快速、简便、不需要获取本市近30年日值降雨数据等优点,并且线性插值法的快速估算是以《导则》给出的准确设计降水量与年径流总量管控率为数值区间,在区间中对未知量进行的函数估算,因此其估算结果可保证较高的准确率。借助线性插值法可大大地避免规划设计者在编制海绵城市专项规划时需要重新统计万余条降雨数据的工作量,且能缓解部分学者从事相关科研工作时无法获得降雨数据的困境,该方法具有着较好的可推广性。

