磁流体球形机器人运动特性研究
赵 欣,司广志,刘新华
ZHAO Xin, SI Guang-zhi, LIU Xin-hua
(中国矿业大学 机电工程学院,徐州 221000)
0 引言
磁流体是一种形态和性能受外加磁场约束和控制的固液二相功能材料,其正常状态下为无磁性的牛顿流体,在外加磁场时,才表现出磁性;球形机器人研究比较广泛,但受到内部驱动结构的限制,控制不够精确,运动不够灵活,难以微型化。磁控机器人是指依靠磁力或磁矩控制驱动运动的机器人。常用的驱动磁场主要有:旋转场、振荡场和场梯度等[1]。由于磁控的特殊性和工作环境要求,目前的对于磁控机器人的研究,较多地集中在微型机器人方面。微型磁控机器人具有体积小、响应快、能耗低、性能可靠等特点,正成为国际研究的热点并被迅速应用到各个领域。把磁流体和软体机器人结合,将磁流体在外部磁场作用下受到的电磁力作为动力源,通过改变外部磁场的大小和方向来控制其运动。
努埃瓦格拉纳达军事大学的Hernando Leon-Rodriguez等人模仿阿米巴虫的运动机制,运用全皮肤运动机制设计了一个磁流体软体机器人[2,3]。第一个球形机器人是1996年的芬兰的Halme等人利用单论滚动改变配重位置进而改变球形机器人重心[4],产生器驱动力矩,驱动球型机器人滚动。德国马普智能系统研究所的团队[5,6]研制了一种毫米尺度的磁控软体机器人,内嵌具有磁性的钕铁硼微颗粒。磁流体和球形机器人结合,磁流体通过外部磁场受到的电磁力作为动力源,通过改变外部磁场的方向和大小来控制其运动。其微型化、运动灵活的特点,可用于人体内疾病诊断和药物运输,磁流体机器人具有重大的研究意义。
1 磁流体球形机器人运动模型
磁流体球形机器人运动简化模型如图1所示,球形机器人表面与地面为纯滚动接触,整个机器人由球壳、内部的磁流体以及球壳与磁流体之间的轻质填充物组成。在梯度磁场作用下,磁流体受到磁力作用;同时,球形机器人与地面接触处,受到摩擦力作用,两个力形成驱动力矩,随着磁力的不断增大,驱动力矩不断增大,当大于球形机器人的滚动阻力矩时,球形机器人开始滚动。
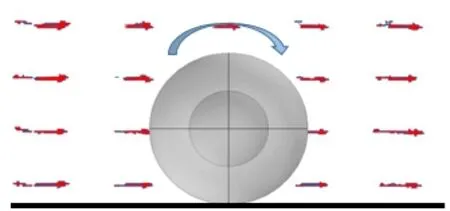
图1 磁流体球形机器人运动简化模型
对磁流体球形机器人进行受力分析(如图2所示),其中,磁流体球形机器人受到的重力G,滚动摩擦系数为δ,半径为R,在梯度磁场下,磁流体受到的磁力为FT,球壳表面与地面接触处不是点接触,应是一部分面积接触。将接触处的作用力简化可得到一力和一力偶,即静摩擦力F和滚动摩擦力偶矩FNδ;随着电流增大,磁场增强,转动力偶矩FTR逐步增大,滚动摩擦力偶矩FNδ也相应增大,当达到极限值FNδMAX,若转动力偶矩FTR继续增大一点,磁流体球形机器人开始滚动,则:
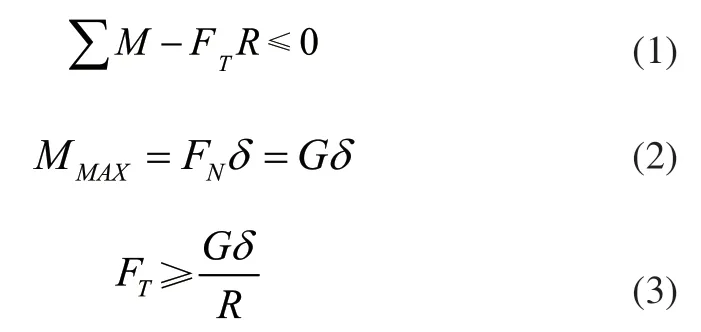
磁流体球形机器人的静摩擦因数为fs,当磁力FT大于静摩擦力的最大值,则:

所以,磁流体球形机器人保持滚动运动磁力FT需满足的条件为:


图2 磁流体球形机器人受力简图
其中,u0为真空磁导率,n为粒子个数,X是粒子磁化率,V是磁流体体积,H是外加磁场强度[8]。因此:
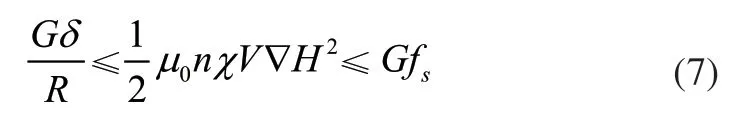
磁流体球形机器人的质心加速度为a,被包裹的磁流体质量为m1,半径为r,球壳质量为m2,半径为R,运用质心运动定律则:

磁流体球形机器人在滚动过程中,只有摩擦力F对质心才有力矩作用,故:

其中,I1=2/5m1R2是磁流体球形机器人对质心的中心轴的转动惯量,I2=2/3 m2r2是球壳对质心的中心轴的转动惯量,β是磁流体球形机器人的角加速度。
由于磁流体球形机器人在地面上无滑动地滚动,所以:

由式(7)~式(10)四个公式得:
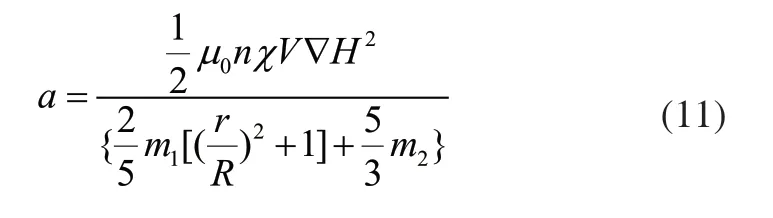
2 均匀梯度磁场仿真分析
COMSOL Multiphysics是一款有限元多物理场分析软件,通过这个软件建立梯度线圈模型,设置位置、电流、磁流体体积等变量,分析不同变量下磁流体在均匀梯度磁场下受力情况,为磁流体球形机器人加速度特性研究奠定基础。
2.1 均匀梯度磁场仿真分析
如图3所示,将两个线圈平行放置,两个线圈的水平距离L是线圈半径R的√3倍,在两个线圈分别通入大小相等方向相反的电流即可产生均匀的梯度磁场。图4是在COMSOL Multiphysics中建立的模型。

图3 梯度线圈
图4 梯度线圈模型
线圈为均匀多匝线圈,匝数为2000,线圈导线电导率为6e7[S/m],线圈导线截面积为1e-6[m2]。图5是线圈通入电流后磁通密度模和磁场的一个分布情况。红色的箭头是磁场线的一个变化情况。图5反映了磁通密度模在梯度线圈轴向的一个分布情况。图6中的两个峰值位置对应两个梯度线圈的位置,两条红线中间区域是梯度线圈产生的均匀梯度磁场。
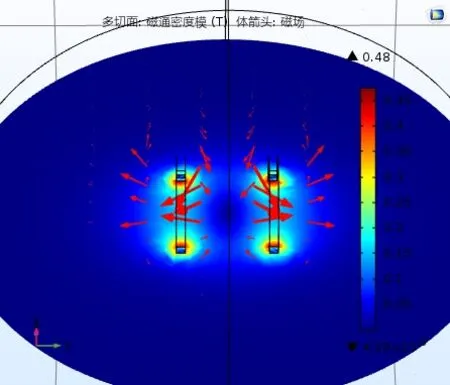
图5 梯度磁场仿真过程图
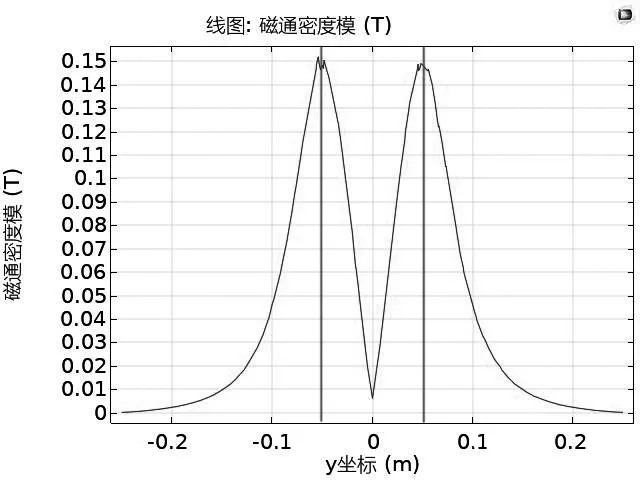
图6 梯度磁场分布图
2.2 磁流体在均匀梯度磁场下的受力仿真分析
在COMSOL Multiphysics中生产我们需要的均匀梯度磁场后,我们需要将磁流体放入均匀梯度磁场中,通过改变变量位置、电流、磁流体体积得到磁流体在均匀梯度磁场下的受力情况,为磁流体球形机器人的控制奠定基础。
2.2.1 磁流体磁化性能分析
磁流体是一种超磁性材料,磁性材料都具有一定的磁滞现象,测试时随磁场的变化,使得磁感应强度发生变化,通过实验测得60组磁场强度H(A/m)和磁感应强度B(T)的数值,并绘制出磁流体的磁化曲线。图7是通过实验后绘制出的磁流体的B-H曲线图。
如图7所示,随着磁场强度H(A/m)的不断增大,磁感应强度B(T)也呈现增加趋势,但增加的速度会随着磁场强度H(A/m)的不断增大而逐渐减小直至到达磁流体的饱和磁化强度。有了磁流体的B-H曲线,才能计算出磁流体在均匀梯度磁场下的具体受力情况。
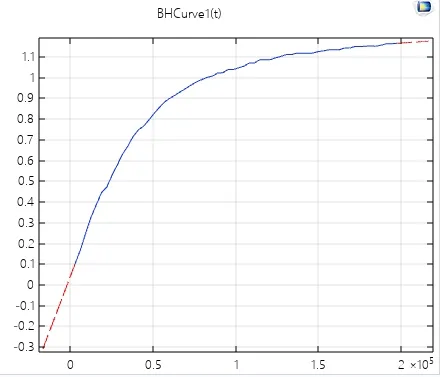
图7 磁流体磁化曲线图
2.2.2 磁流体COMSOL Multiphysics受力仿真分析
如图8所示,将磁流体设置成球体放置在梯度线圈中间,设定磁流体的具体材料参数,将上述磁流体的B-H曲线作为材料属性导入,其磁场模、磁通密度模、normB、normH均来自次u流体的B-H曲线,物理场选择磁场,在磁场物理场下为磁流体添加安培定律,并在安培定律的磁场选项中选择B-H曲线;同在磁场物理场下,为磁流体添加计算力选项,当变量位置、电流、磁流体体积变化时,计算磁流体受到的电磁力。图9是仿真过程中的效果图。

图8 磁流体受力分析模型

图9 磁流体受力分析过程图
如图10所示,把磁流体的位置设置为0.02m,半径设置为0.005m,电流取值范围为1~45A,间隔为5A。可以看到在一定的电流大小范围内,磁流体受到的磁场力随着电流的增大不断增大,但其增长速度随着电流的增大先增大后变小,这是受其本身材料性质的影响而导致的结果。
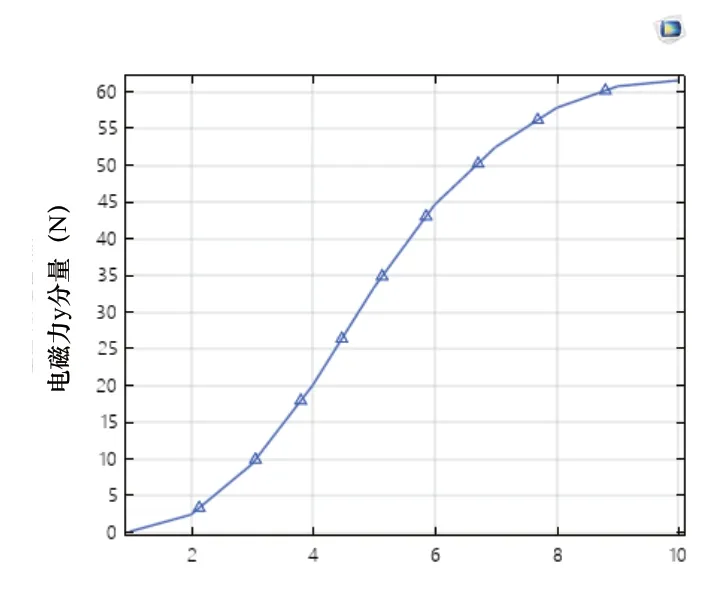
图10 电磁力FT随线圈电流变化图
2.3 磁流体球形机器人加速度仿真分析
2.3.1 磁流体在磁场中的位置变化对加速度的影响
如图11所示,线圈圈数取20匝,电流为1A,磁流体的位置从0.02m处逐渐移动至0.03m处,磁流体受到的电磁力呈上升趋势。
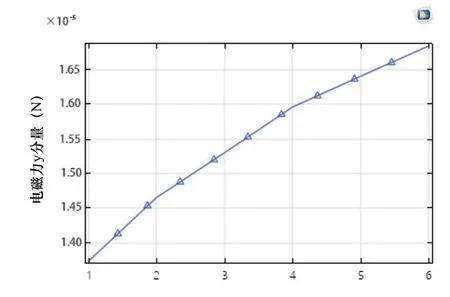
图11 电磁力FT与位置变化关系图
在ADAMS中建立如图12所示的磁流体球形机器人运动模型,磁流体球固定在球壳内部,并分别赋予它们相应的材料;地面设置为硬质地面,球壳与地面建立solid-solid类型的接触力;地面的静摩擦系数为0.3,动摩擦系数为0.1[9~11]。磁流体球形机器人运动模型的具体参数为:球壳的半径为0.0075m,密度为1.1kg/m3,磁流体的半径为0.005m,密度为1370kg/m3。
根据图11中位置变化而产生的电磁力FT变化的数据,运用step函数,在0~3s时段内,间隔为0.5s,分别设定电磁力FT为1.281e-5N,1.37e-5N,1.47e-5N,1.53e-5N,1.60e-5N,1.64e-5N,1.69e-5N。

图12 磁流体球形机器人运动模型
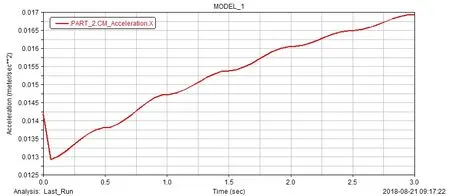
图13 加速度与位置变化关系图
如图13所示,图中展示了加速度随时间的变化,在时间区间0~3s内,随着电磁力FT的逐渐增大,磁流体球形机器人的加速度a呈现一个上升趋势。可以看出,均匀梯度磁场下的磁流体球形机器人的加速度与线圈的距离呈正比关系,根据这一规律,在磁流体球形机器人运动过程中,可通过改变电流的大小来保持其速度的稳定性、可控性。
2.3.2 线圈电流变化对加速度的影响
由于磁流体球形机器人滚动所需要的力并不大,所以我们着重研究电流较小时的电磁力变化。如图14所示,电流取值范围为0.1~1A,间隔为0.1A,位置为0.02m。可以看到,在电流取值较小时,随着电流的增大,电磁力FT呈现一个指数型上升趋势。
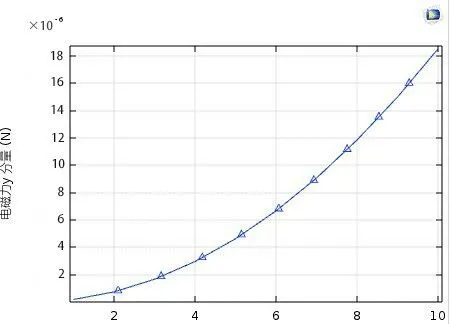
图14 电磁力FT与线圈电流变化关系图
同样将图14中的数据代入ADAMS中,如图15所示,磁流体球形机器人在电流变化引起的电磁力FT的作用下,其加速度、速度、位移呈现一个指数型增长;这对通过改变电流的大小来保持其速度的稳定性、可控性具有参考意义。

图15 加速度与线圈电流变化关系图
2.3.3 磁流体体积变化对加速度的影响
如图16所示,当磁流体在梯度磁场的中的位置和电流不变时,改变磁流体的体积,随着体积的逐渐增大,磁流体受到的电磁力FT呈指数型增加。同样,随着磁流体体积的增加,磁流体球形机器人受到的滚动阻力矩也会呈现指数型增加,其加速度的变化取决于电磁力FT和滚动阻力矩两个变量,哪一个变量增加的速度快。

图16 电磁力FT与磁流体体积变化关系图
将磁流体体积从0.001m增加到0.005m,这一过程中的电磁力FT和体积变化量作为ADAMS的两个设计变量,经过参数化建模后,进行优化仿真。

图17 加速度与磁流体体积变化关系图
在两个设计变量的作用下,磁流体球形机器人的加速度变化如图17所示,加速度增加速率在减小并逐渐趋于平缓,随着磁流体体积的增加,先是电磁力FT起主导作用,进一步,由于体积增加而引起的滚动阻力矩对加速度的影响逐步增大,根据这一规律,可合理分配磁流体在磁流体球形机器人中的体积占比。
3 结论
磁流体球形机器人在均匀梯度磁场中的位置变化、线圈的电流大小变化以及磁流体体积的变化对磁流体球形机器人的加速度都有不同程度的影响。磁流体球形机器人在逐渐靠近一侧线圈运动过程中,加速度呈线性增大;线圈电流逐渐增加的过程中,加速度呈指数型增大;磁流体体积在一定的范围内增大过程中,受电磁力和滚动阻力矩两个变量的影响,加速度呈增大趋势,但其增大速率不断减小。
研究以上三个变量对磁流体球形机器人加速度的影响,为磁流体机器人的控制提供了理论参考。

