非金属原子边缘修饰InSe纳米带的磁电子学特性及应变调控*

李野华 范志强 张振华

(柔性电子材料基因工程湖南省重点实验室, 长沙理工大学物理与电子科学学院, 长沙 410114)

利用基于密度泛函理论的第一性原理计算方法, 研究了Se边用H饱和、In边用各种非金属元素X(X=H, B, N, P, F 和 Cl)端接的锯齿型 InSe 纳米带 (H-ZN(7)-X)的几何结构、磁电子特性及应变效应.计算的形成能和Forcite退火模拟表明H-ZN(7)-X具有稳定的几何结构.F和Cl端接时, 纳米带具有和H端接时类似的磁金属性质.N端接时, 纳米带磁性最强.但B和P端接使得纳米带边缘的磁性完全消失.特别是, 我们发现外加的机械应变可以增强H-ZN(7)-N磁稳定性, 并且有效地调节费米能级处的自旋极化率(SP), 能在0—92%之间变化, 这意味着可设计机械开关来控制低偏压下的自旋输运.应变调制机制与应变诱导的键长变化导致不成对的电子的重新分布或消失有关.N-ZN(7)-N的磁性主要来源于In, Se及N原子的p轨道, 这对于研发非过渡金属磁性材料有重要意义.

1 引 言

自从石墨烯被发现以来, 低维纳米材料的电子及磁性问题被广泛研究[1−8].一般说来, 本征 2维(2D)材料很少具有磁性, 而相应的纳米带由于存在边缘态, 可能具有磁性, 如石墨烯纳米带[9], 硅烯纳米带[10]及MoS2纳米带[11]等.但这些边磁往往不稳定, 特别在较高温度下, 其磁性可能消失.所以, 为了进一步调整纳米带的磁性, 研究者们提出了诸多有效的方法[9−15].其中, 边缘修饰法被认为是一种重要的方法.例如Zhang等[16]报道, 当锯齿型石墨烯纳米带(ZGNRs)边缘用-OH进行边缘端接时, 由于纳米两边的自旋相互影响, ZGNRs表现出自旋半导体性质, 但把ZGNRs的上下边缘分别用羟基和-SO2(或-NO2)基团进行端接时, 形成一种非对称的纳米带结构, 使得ZGNRs由最初的自旋半导体转变为半金属性[17].锯齿型MoS2纳米带是铁磁金属, 但通过边缘H端接后, 它的磁性态被大幅度地增强, 可以比ZGNRs的磁性强很远.边缘O原子端接使得P原子和O原子的pz轨道发生成键作用, 导致锯齿型磷烯纳米带(ZPNRs)表现为磁性基态[18].因此, 寻找合适的边缘修饰以改善纳米结构的磁性是非常必要的.

作为2D材料家族的新成员, 单层InSe最近已被成功制备[19].多层InSe的载流子迁移率在室温和液氦温度下分别超过 103和 104cm2·V–1·s–1[20].有趣的是, 多层InSe的有效质量周期性地决于其层厚度[21].二维InSe表现出比磷烯更高的环境稳定性, 并且在室温下拥有比过渡金属二硫化物更高的载流子迁移率[22].此外, 原子层厚度的InSe具有极强的光敏反应和较快响应时间[19], 这使其成为光电应用的重要候选者.最近, 密度泛函(DFT)计算表明锯齿型InSe纳米带具有本征较强(约0.5—0.7 µB/单胞)的 FM 基态磁性, 并且磁性仅分布在纳米带的其中一个边缘[23].同时, Yao等[24]研究表明, 锯齿边缘InSe纳米带的I-V特性曲线表现了较强的负微分电阻效应和自旋极化现象.此外, 通过掺杂可以有效地调节锯齿型InSe纳米带的磁性, 其中p型掺杂可以使它变成“富含”In原子边缘出现自旋极化的半金属[25].

本文研究了Se边用H饱和、In边用各种非金属元素X(X= H, B, N, P, F 和 Cl)端接的锯齿型InSe纳米带(H-ZN(7)-X)的几何结构、磁电子特性及应变效应.结果表明, H, F 和 Cl原子端接后, 纳米带具有类似的磁金属性质.N原子边缘饱和可以增强纳米带的磁矩、自旋极化率以及磁稳定性, 而B和P原子端接则使纳米带的磁性消失.同时还发现, 外部施加的机械应变可以增强磁稳定性并且有效地调节纳米带在费米能级处的自旋极化率 (SP), 最小几乎为零, 最高可达 92%.这意味着可设计一致机械开关来控制低偏压下的自旋输运.

2 计算方法

对于我们设计的所有结构, 在 Atomistix ToolKit (ATK)[26,27]中实现基于 DFT 的第一性原理方法的几何优化和电子、磁性质计算, 这种方法得到广泛应用[28−32].为求解Kohn-Sham方程,选择 Perdew-Burke- Ernzerhof (PBE) 泛函或自旋广义梯度近似(SGGA)作为计算非磁性态或磁性态的交换相关泛函.采用Troullier-Martins模守恒赝势表示原子核和原子轨道的线性组合, 来扩展电子的价态.考虑到原子的电极化效应, 所有原子均采用双 z加极化 (DZP)基组.k点采样在x,y和z方向上分别为 1 × 1 × 100, 其中z是周期方向, 截断能设置为 150 Ry (1 Ry= 13.606 eV).对于所研究的模型, 沿着一维长度方向施加周期性边界条件, 在另外两个方向使用20Å的真空层来消除模型与其“像”之间的相互作用, 所有的计算都在几何模型被优化直到每个原子的残余力在0.01 eV/Å以下后进行.为了简单起见, 在电子结构的所有计算中将费米能级EF设置为零.

3 计算结果与分析

3.1 结构及稳定性

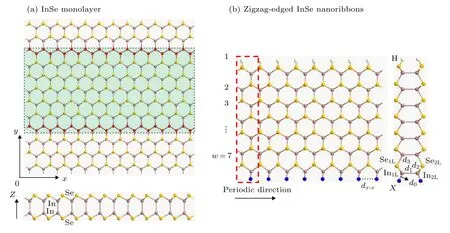
图1 (a) InSe单层的顶视图(上图)和侧视图(下图).沿着X方向裁剪InSe单层可以得到锯齿型InSe纳米带, 图中淡绿色填充区域表示; (b) H-ZN(7)-X的顶视图(左图)和侧视图(右图).红色的虚线框表示计算的单胞Fig.1.(a) Top and side views of monolayer InSe.Tailoring monolayer InSe along X-axis direction to achieve zigzag InSe nanoribbons, denoted by a pale green filled area; (b) top and side views of H-ZN(7)-X.The red dotted box represents a unit cell.

图1(a)给出单层InSe的原子结构, 它有四个原子层, 层内通过Se-In-In-Se方式成键结合.它的晶格常数约为1Å.当沿着x轴的晶格方向裁剪2D InSe单层时, 可以得到一种锯齿型边缘类型纳米带, 并由图1(a)中的淡绿色填充区域表示.按照以前的惯例, 锯齿型纳米带的宽度定义为宽带方向锯齿形 In-Se 原子链的数量n.这里, 以n= 7 为代表, 锯齿型纳米带如图1(b)所示, 红色虚线框表示锯齿型纳米带的一个单胞.我们的研究表明, H饱和的锯齿型InSe纳米带的磁性只出现在In边缘(下边缘), 所以, 在本文中仅仅考虑把下边缘用其他不同的非金属原子X(X= B, N, P, S, F,Cl)替换H原子而进行化学修饰, 上边缘保持用H饱和, 以考察不同的非金属原子对磁性的调控,相对应的纳米带记为H-ZN(7)-X.另外, 把下边缘Se(In)和相邻的In(Se)原子分别表示为SeiL(IniL)(i= 1,2), 相应的键长分别为d1,d2,d3, 其 中In1L与X原子以及X原子之间的键长表示为d0和dX–X, 如图1(b)所示.

为了检验几何结构优化后在能量上相对本征纳米带的稳定性, 计算其形成能, 定义为[33]:EFE=(ETR–EBR–nHEH–nXEX)/L0, 式中ETR和EBR分别是纳米带H-ZN(7)-X和裸边纳米带一个单胞的总能量,EX(EH)和nX(nH)分别是一个孤立的X(H)原子的能量和一个单胞中端接的X(H)原子数量,L0是单胞在纳米带方向上的晶格常数.根据定义, 具有负的形成能表明相应的结构在能量上是稳定地, 并且在实验中也许可以存在.形成能越低,结构越稳定.可以清楚得看到, 所有边缘端接的HZN(7)-X的形成能EFE都是较低的负值, 这表明这些边缘功能化的结构在能量上是稳定的, 因为它们在形成H-ZN(7)-X时是一个放热过程.我们知道,H原子边缘端接是维持纳米带结构稳定的常用方法, 而我们发现纳米带用其他原子X(= B, N, P,F, Cl)端接的情况有着明显比H原子端接更低的形成能, 尤其明显的是N原子端接的情况.

为了检测所研究模型的热力学稳定性, 我们进行了Forcite退火的模拟计算.在整个过程中, 使用4个退火循环过程.每个退火循环的中点处的初始温度设定为300 K, 温度最大值则设定为500或 600 K.以 1 ps的动态时间步长运行 8 ps后, 作为代表的几条纳米带的几何结构如图2所示, 在纳米带模拟 8 ps后, 可以看到 H-ZN(7)-B 在 500 K时出现小变形, 而其他纳米带则在600 K时才出现较小的形变, 但都没有观察到边缘重建现象, 这表明非金属原子边缘端接的H-ZN(7)-X热稳定性较高.同时, 可以见到N原子和P原子各自形成强劲的非极性共价键(见图2(b)和图2(e)).

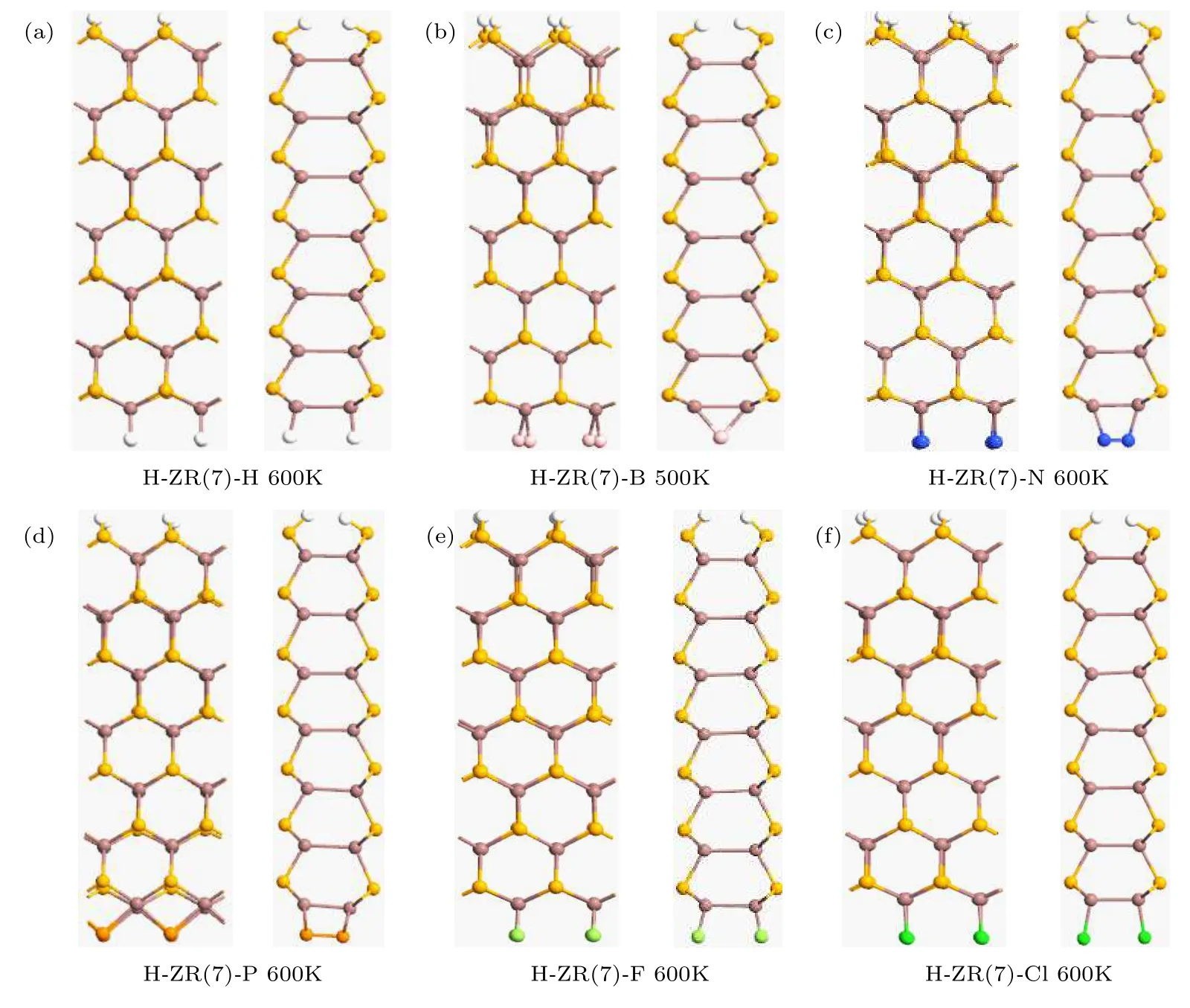
图2 使用 BOMD 模拟检测 H-ZN(7)-X 的热稳定性.在 8 ps 模拟后, 对于 H-ZN(7)-H, H-ZN(7)-N, H-ZN(7)-F, H-ZN(7)-P 和 HZN(7)-Cl, 在600 K时出现小变形, 对于H-ZN(7)-B在500 K处出现小变形, 但是没有观察到边缘重构Fig.2.BOMD simulations for examining thermal stability of the H-ZN(7)-X.The small deformations occur at 500 K for H-ZN(7)-B and 600 K for other ribbons after 8 ps of simulation, but no edge reconstruction is observed.

3.2 无磁态电子结构

图3(a)—图3(f)给出了H-ZN(7)-X在自旋非极化条件下即无磁(NM)态时能带结构(BS)、态密度(DOS)及投影态密度(PDOS).这里的PDOS为分别投影在纳米带最外边缘的Se(与H原子成键)和In(与X原子成键)原子以及X原子上的DOS.以表明它们各自对整体电子结构的贡献.很显然, H-ZN(7)-X在不同原子端接情况下始终保持金属特征, 只是穿过费米能级的两条能带a1及a2的形状发生了变化.从 PDOS来看, 对于 HZN(7)-F和H-ZN(7)-Cl, 边缘In对其强金属性有重要贡献.而对于H-ZN(7)-N, 端接原子N对强金属性有重要贡献, 这说明边缘X原子的端接对其电子性质有明显的影响.另外, 从图3(g)来看, 子能带a2均是由纳米带的下边缘原子所贡献, 但对于子能带a1, 除了H-ZN(7)-B之外, 都是由纳米带的上边缘原子所贡献, 类似于H-ZN(7)-H的情况.在H-ZN(7)-B纳米带中, 上下边缘都对子能带a1有部分贡献, 尤其是其下边缘 B 原子.另外, 与纳米带H-ZN(7)-H相比, H-ZN(7)-B的费米能级上方出现许多新能带, 甚至还有除子能带a1和a2之外的第三条子能带穿过费米能级(见图3(d)).从其PDOS来分析可以发现, 这些较为集中出现的能带主要是下边缘的B原子所贡献.这充分说明, 由于B原子的端接作用, H-ZN(7)-B的电子结构发生较大的变化.另外还发现, 对于子能带a2,H-ZN(7)-H, H-ZN(7)-N, H-ZN(7)-F 及 H-ZN(7)-Cl在G点的带首都在费米能级上, 而H-ZN(7)-B和H-ZN(7)-P在G点的带首相对于EF明显上移了许多.特别是, H-ZN(7)-N子能带a2在Z点的带尾发生了明显移动, 并与子能带a1在Z点重叠.

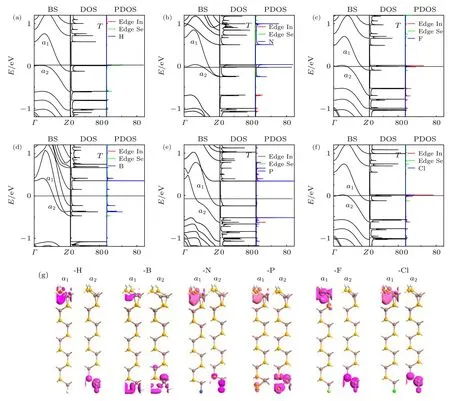
图3 (a)−(f) 分别为 H-ZN(7)-H, H-ZN(7)-B, H-ZN(7)-N, H-ZN(7)-P, H-ZN(7)-F, 和 H-ZN(7)-Cl在 NM (无磁) 态下的的能带结构(BS)、态密度(DOS)和最外边缘Se (In)原子的投影态密度(PDOS); (g)费米能级附近能带a1 (a2)相对应的部分电荷密度分布.等值面设置为 0.05|e|Å–3.Fig.3.(a)−(f) Correspond to the band structure (BS), density of the state (DOS), and projected density of the state (PDOS) of HZN(7)-H, H-ZN(7)-B, H-ZN(7)-N, H-ZN(7)-P, H-ZN(7)-F, and H-ZN(7)-Cl, respectively; (g) the partial charge density distribution corresponds to subbands a1 (a2) labeled in figures (a)−(f), respectively.The isosurface value is set as 0.05|e|Å–3.

3.3 磁结构和磁电特性

接下来, 计算纳米带在自旋极化下的磁性质,分别考虑铁磁(FM)和反铁磁(AFM)两种磁耦合, 以发现能量上优化的磁耦合态.初始的FM状态被设置为所有原子的自旋指向相同的方向, 而初始AFM状态则被设置为三个不同的磁构型, 即把两个相对边缘、在相同的边缘两个相邻原子或两个相邻的单胞边缘原子的自旋设置为反平行的.然而, 计算结果表明, 对各种初始自旋设置, 最终磁序总是收敛到FM态, 这表明非金属原子边缘端接的锯齿形纳米带具有本征的FM态磁序.为了确定纳米带的磁基态, 下面计算磁化能, 其定义为EM=(ENM–EFM)(以 meV/单胞为单位), 其中ENM和EFM分别是自旋非极化无磁性态下和FM状态下的能量, 结果如表1 和表2 所示.可以看到, H-ZN(7)-B和H-ZN(7)-P的EM为0, 这说明它们没有磁性.其他纳米带的EM都是正值, 尤其是H-ZN(7)-N,高达 78.32 meV/单胞, 表明它有很好的磁性稳定性.

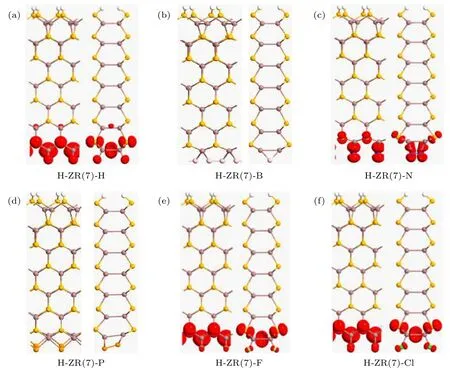
图4 自旋极化电荷密度等值面图, 等值面取为 ± 0.005|e|/Å3 (a) H-ZN(7)-H; (b) H-ZN(7)-B; (c) H-ZN(7)-N; (d) H-ZN(7)-P;(e) H-ZN(7)-F; (f) H-ZN(7)-ClFig.4.The isosurface plots for the spin polarized density.The isosurface value is 0.005|e|/Å3:(a) H-ZN(7)-H; (b) H-ZN(7)-B; (c) HZN(7)-N; (d) H-ZN(7)-P; (e) H-ZN(7)-F; (f) H-ZN(7)-Cl.

为了呈现磁性的空间分布, 计算了自旋极化电荷密度:即 a-自旋 (红色)和 b-自旋(蓝色)态的电荷密度差 (∇r=ra–rb), 如图4(a)—图4(f)所示.很明显 H-ZN(7)-B和 H-ZN(7)-P是无磁的,进一步验证了上文中它们的磁化能EM为0的结果.而 H-ZN(7)-F, H-ZN(7)-Cl及 H-ZN(7)-N 的上边缘没有磁性, 磁性集中在下边缘, 与H-ZN(7)-H情况相同.同时, 我们也计算了各种纳米带的磁矩, 发现 H-ZN(7)-N 的磁矩是最大的, 约 0.632 µB/单胞, 其他磁性纳米带的磁矩约为0.44—0.47 µB/单胞.此外, 它们的磁分布是不同的, H-ZN(7)-H,H-ZN(7)-F与H-ZN(7)-Cl的磁矩主要是由下边缘的In原子所贡献.而对于H-ZN(7)-N, 它的边缘N原子磁矩为0.52 µB, 是其边缘磁性的主要来源.怎样理解不同边修饰时, 磁性的产生或消失？当用H端接ZN(7)两边时, 在几何优化后它的上边缘的悬挂键被完全饱和但下边缘的悬挂键尚未完全消除, 所以仅仅它的下边缘存在磁性.众所周知,边磁对边缘结构非常敏感, 在 H-ZN(7)-F, HZN(7)-Cl及 H-ZN(7)-N 模型中, F, Cl, N 端接时,下边缘结构基本与H端接类似(见图4), 所以下边缘保持磁性.而在H-ZN(7)-B和H-ZN(7)-P模型中, B及P端接时, 下边缘结构与H端接相比, 变形较大, 键长及键角有明显的不一样, 使得边缘原子的磁耦合改变, 原子内非成对电子(unpaired electrons)不复存在, 从而导致下边缘磁性消失.这充分反映“结构-特性”的依赖关系.

图5(a)—图5(d)所示为自旋极化的能带结构(BS)、态密度(DOS)和原子投影态密度(atom-PDOS), 其中atom-PDOS是指DOS分别投影到在纳米带下边缘的In/Se原子以及X原子上的DOS, 可以表明它们各自对整体电子结构的贡献.可以看出, H, F 和 Cl原子端接时, 纳米带磁性能带具有类似的结构, 由下边缘原子所贡献的子能带a2发生了自旋分裂, 这是因为下边缘引入了磁性, 多子及少子占据的能带不同, 而子能带a1是自旋简并的, 由于上边缘没有磁性.这些与图3(g)和图4(a)、图4(c)、图4(e)、图4(f)的情况相符合.另外, 从PDOS来看, 它们的SeL和InL所贡献的态密度都是高度自旋分裂的, 这与表1所得出的结论相 对 应, 即 H-ZN(7)-H, H-ZN(7)-F 与 H-ZN(7)-Cl的总磁矩主要是由下边缘的In原子, 尤其是Se 原子所贡献.有趣的是, 对于 H-ZN(7)-N, 与无磁态相比, 其子能带a2发生了高度自旋分裂, 即它的a-自旋能带(a2(a))大幅度地向下移动, 而b-自旋能 (a2(b))带则向上升.H-ZN(7)-N这种巨大的自旋分裂(能量偏移)现象与它具有较强的磁性(大磁矩)有关, 如表2 所列.另外, 从 H-ZN(7)-N的atom-PDOS来看, 边缘的N原子在费米能级附近是自旋极化总态密度的主要贡献者.这说明N原子在很大程度上影响了它的磁电子学性质.

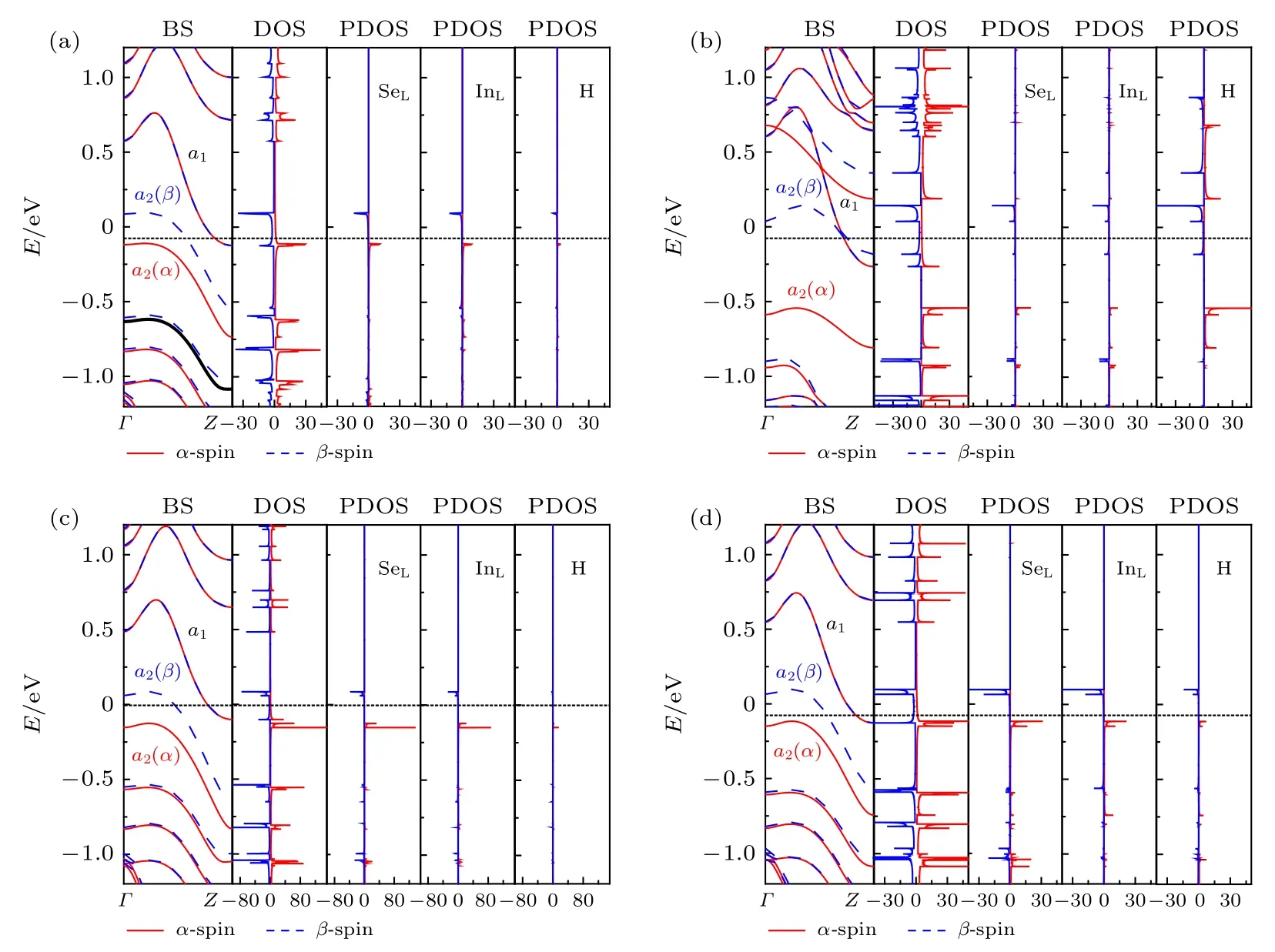
图5 (a)−(d)分别为 H-ZN(7)-H, H-ZN(7)-N, H-ZN(7)-F 和 H-ZN(7)-Cl在 FM 态下的的能带结 (BS)态密度 (DOS)和投影态密度(PDOS)Fig.5.(a)−(d) Correspond to the band structure (BS), density of the state (DOS), and projected density of the state (PDOS) of HZN(7)-H, H-ZN(7)-N, H-ZN(7)-F and H-ZN(7)-Cl in the FM state.

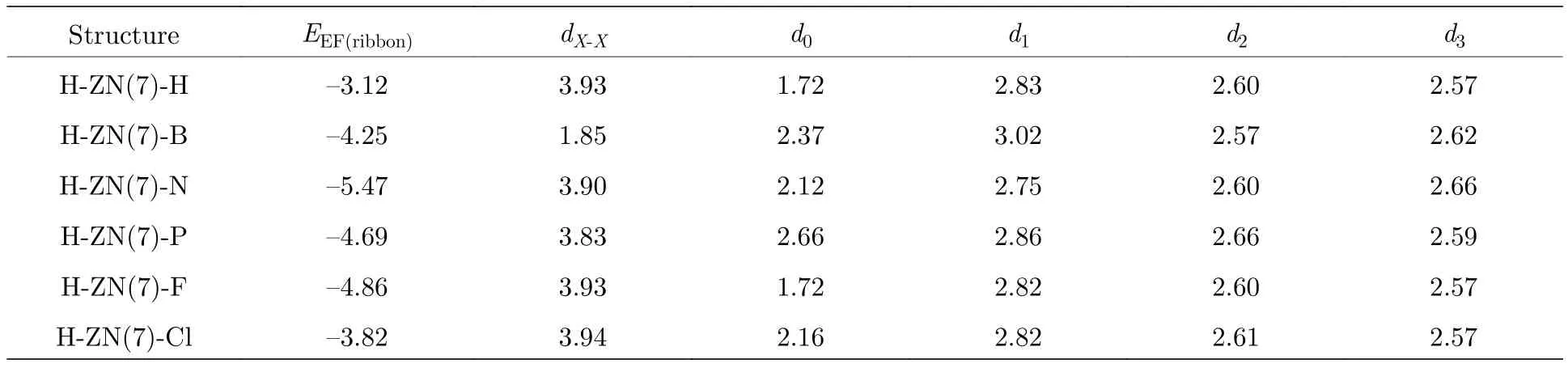
表1 H-ZN(7)-X 的形成能 (EFE) (单位:eV/原子)和键长或两相关原子间的空间位置 (单位:Å)Table 1.The formation energy (EFE) (unit:eV/atom) of H-ZN (7)-X and the bond length or space position between the two related atoms (unit:Å).

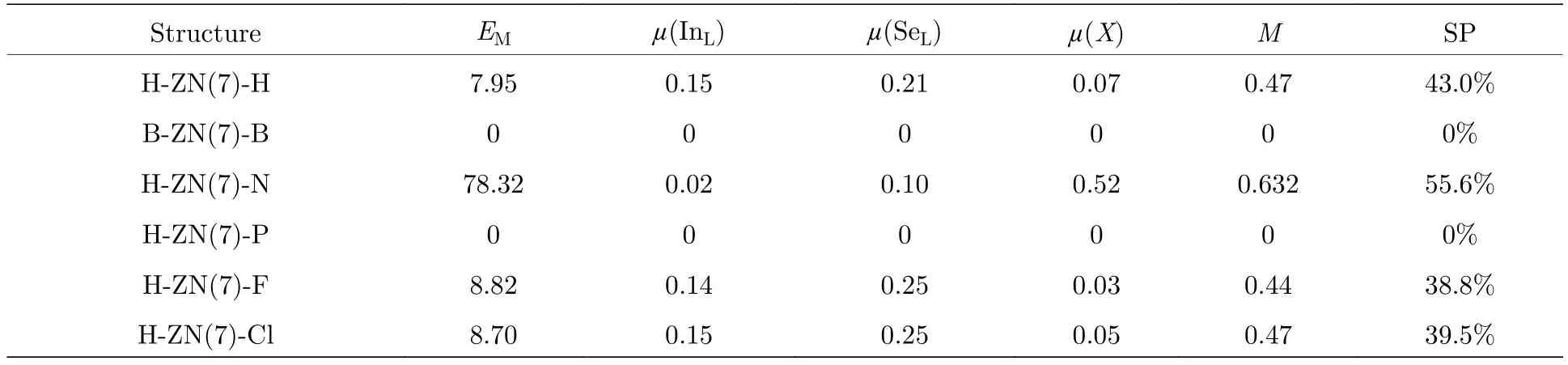
表2 H-ZN(7)-X 在铁磁态 (FM)的结构参数.M, µ(InL), µ(SeL), µ(X)分别为总磁矩和下边缘 In, Se 和 X 的磁矩 (单位:µB/单胞).EM和SP分别是磁化能(单位:meV/单胞)与费米能级处的自旋极化率Table 2.The structural parameters of H-ZN(7)-X in the FM state.M represents the net magnetic moment of unit cell,µ(InL), µ(SeL) and µ(X) represent the net magnetic moment of lower (L) edge In, Se and X atoms, respectively(unit:µB/unit cell).EM represent the magnetized energy (unit:meV/unit cell) and SP is the spin polarization efficiency at the Fermi level.

另外, 自旋极化率是研究磁金属材料磁输运性能的一个重要物理量.所以, 我们也计算了费米能级处的自旋极化效率, 定义为100%, 其中Db和Da分别是 b-自旋和 a-自旋状态的费米能级处的DOS.零值表示不发生自旋极化, 负值表示反向自旋极化发生.可以发现, 不同非金属原子X对纳米带在费米能级附近的自旋极化率 SP具有明显的调节作用, 使得其值从39.5%变化到55.6%, 其中H-ZN(7)-N的SP最高(55.6%), 如表2 所列.

3.4 应变效应

通过应变效应来调节材料的电磁特性是纳米电子学研究中常用方式之一.这里以N原子端接的H-ZN(7)-N为例, 探索磁电子特性的机械应变调控效应.考虑沿其锯齿方向施加的单轴应变e,其定义为e= (L–L0)/L, 其中L0和L分别是平衡态和应变下纳米带方向上的晶格常数.为了说明在不同应变下磁性的变化, 计算了费米能级处的自旋极化率SP, 其定义如上文所述.这里只计算拉伸应变的影响, 因为它易于在实验上实现.计算结果如图6(a)所示.可以看到, SP的变化对应变较为敏 感.当 应 变e≤ 12% 时, SP 值维持在大约52%—60%的范围内, 变化曲线较为平缓, 无明显突变.然而当e= 14%, SP 急剧上升至最大值约92%, 然后在e= 16%时又几乎直线下降到仅约3%, 接着在e= 18% 时下降到几乎为 0 (约 0.4%).这意味着可设计机械开关来控制低偏压下的自旋输运.值得指出的是, 自旋极化率SP在拉伸应变e超过20% 以后开始转为小的负值, 这说明反向自旋极化发生.

为了检验所施加的拉伸应变是否引起了塑性形变, 计算纳米带的应变能, 其定义为EM= (Es–Eus), 其中Es和Eus分别是一个单胞在有应变和无应变时的能量, 计算结果如图6(a)红色曲线所示.很明显, 应变能随应变增加而平滑增加, 基本上是二次抛物线的形式, 即满足 DE=ke2, 这表明施加的应变仅发生在弹性范围内, 因此是完全可逆的过程.另外, H-ZN(7)-N一个单胞中的磁矩(M)和磁化能(EM)与应变的关系如图6(b)所示.很显然,在e= 14%之前, 总磁矩随着应变的增加而略微减小, 但在e> 14% 以后, 总磁矩呈现上升趋势,磁性增强.N原子的磁矩与总磁矩几乎同步变化,这说明不管是否施加应变, N原子始终是总磁矩的主要贡献者.同时还可以看到, 磁化能EM的变化与总磁矩也几乎同步, 即在较高的机械应变下, 磁稳定性增加, 这是因为一般说来体系较高的总磁矩对应较高的磁稳定性.

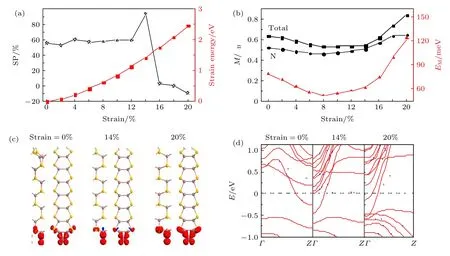
图6 (a)拉伸总能和费米能级处自旋极化率随拉伸形变的变化; (b)磁矩及磁化能随拉伸形变的变化; (c), (d)几个典型形变0%, 14%, 20% 下的自旋极化电荷密度和能带变化.等值面被设为 ± 0.005|e|/Å3Fig.6.(a) The evolution of spin polarization efficiency (SP) at the Fermi level and the strain energy versus strain; (b) the magnetic moment (M) and magnetized energy(EM) in one unit cell versus strain; (c) the spin polarized density and (d) the band structure at several typical strains.The isosurface value is set as 0.005|e|Å–3.

为了直观地呈现不同应变下磁性的变化(未成对的电子再分布), 我们计算了几个典型应变时的自旋极化电荷密度, 如图6(c)所示.显然, 在不同应变下, 自旋极化电荷密度主要分布在N原子上,并与图6(b)中N原子的磁矩以及总磁矩计算情况一致, 如在e= 20% 时, 纳米带下边缘有最强的磁性.相应的能带结构与应变的关系如图6(d)所示.明显地, 纳米带在不同应变下一直保持磁金属性质, 但费米能级附近的b-自旋子带及其他邻近的子带随应变发生明显的移动, 以致改变费米能级上的 DOS, 最终导致 SP 的变化.特别是, 对于e=20%, 费米能级上的a-自旋态具有比b-自旋态稍微较高的DOS, 导致此处出现小的负SP, 即小的反向自旋极化.

一般来说, 应变效应调节电子特性和磁性的机制非常复杂.它包含了键长和键角的不规则变化,进而改变了轨道重叠、成键强弱和电荷分布等情况.其中键长的改变对磁性起着至关重要的作用,因为它可以通过成键类型的竞争来导致未配对电子重新分布.当键长增长时, 将减少(增加)共价键(离子键)成分, 但键长缩短时恰恰相反.前者增加未配对电子而提高磁性.如图7(a)所示, 可以看到, 键长d0,d1及d2变化非常缓慢.有趣的是,dN-N随着应变的增加几乎是直线上升的, 在e= 20%时, 大幅增加到 4.69 Å.所以, N—N 键长明显变长将导致离子键成分增加, 即未配对电子数目增加,磁性增强.这一点可从e= 20%时的自旋极化电荷密度图清楚看出(图6(c)).图7(c)和图7(d)所示为在应变效应下, 所有原子(T)和N原子的p轨道的PDOS的变化情况.作为比较, 没有应变的情况也图示于 7(b).可以看到 p轨道的PDOS对应变十分敏感, 特别是在费米能级附近.例如, 在e= 14% 时, 所有原子 (T)和 N 原子的p轨道在费米能级处的b-自旋态密度非常高(见图7(c))、且相对权重显著增大, 导致高度不对称的DOS, 即费米能级处有较高的SP(见图6(a)).当e= 20%时, 所有原子(T)和N原子的p轨道在费米能级处出现的两种自旋的态密度都较小(见图7(d))、并导致小的 SP(见图6(a)).所以, 锯齿型InSe纳米带的磁性主要来源于原子的p轨道且具有应变的灵活可调性.

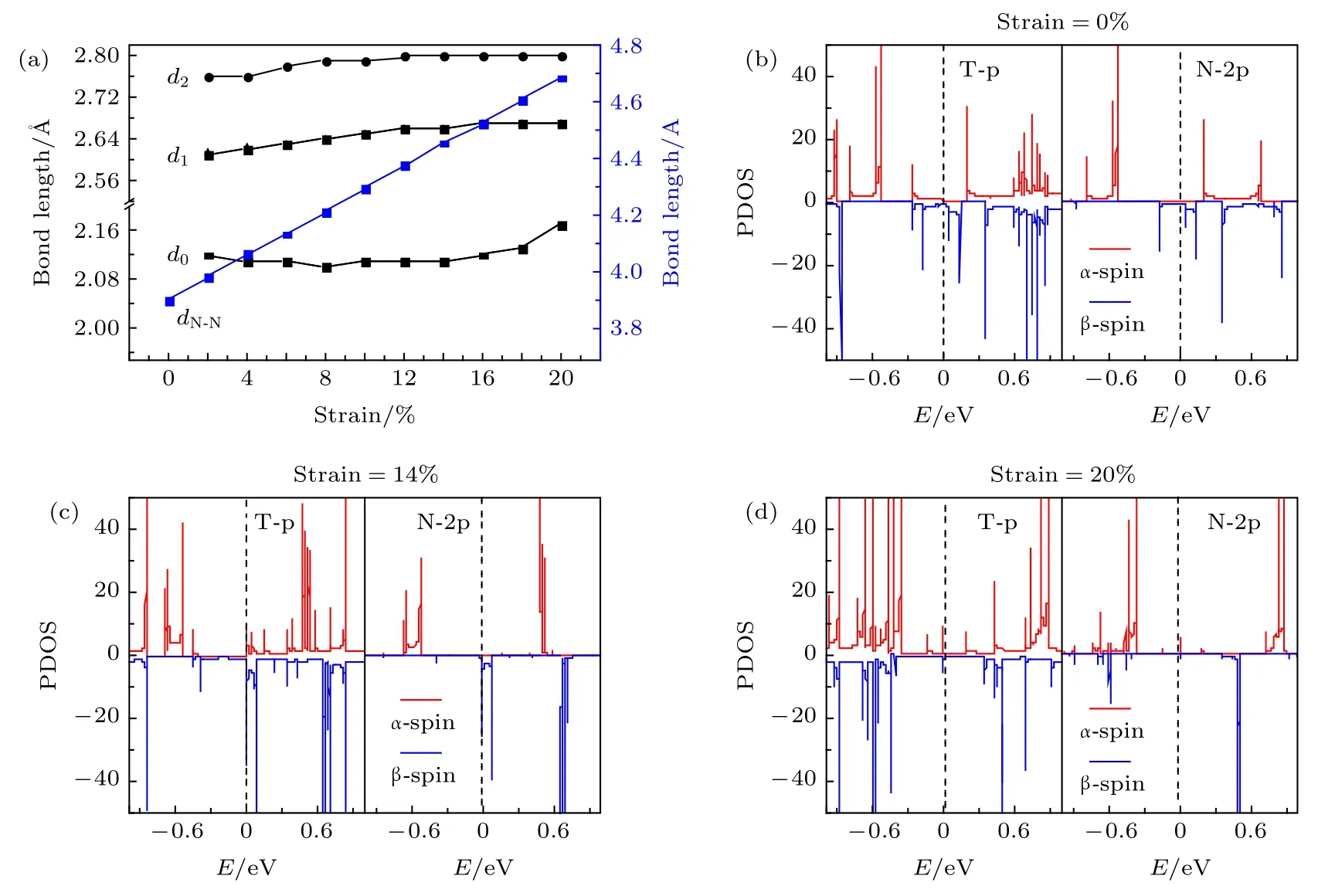
图7 (a)边缘键长随拉伸形变的变化; (b)−(d)几个典型形变 0%, 14%, 20% 下的 p 轨道的态密度 (DOS) T-p 和投影态密度(PDOS)Fig.7.(a) the bond length versus strain; (b)−(d) the p-orbital PDOS of In atoms at the lower edge (InL) and adjacent Se atoms(SeL) upon the the effect changes with strain at e= 0%, 5%, and 16%, respectively.

4 结 论

利用基于密度泛函理论的第一性原理计算方法, 研究锯齿型InSe纳米带边缘修饰, 即在Se边用H饱和及在In边用各种非金属元素X(X= H,B, N, P, F 和 Cl)端接的几何结构、磁电子特性及应变效应.计算的形成能和Forcite退火模拟表明功能化纳米带具有稳定的几何结构.在自旋非极化条件下即 NM 态时, H-ZN(7)-H, H-ZN(7)-F, HZN(7)-Cl和 H-ZN(7)-N金属性强于 H-ZN(7)-B及 H-ZN(7)-P.自旋极化计算表明:F 和 Cl端接时, 纳米带具有和H端接时类似的铁磁基态的磁金属性质.N 端接时, 纳米带磁性最强.但 B 和P端接使得纳米带边缘的磁性完全消失.特别是,我们发现外加的机械应变可以增强H-ZN(7)-N磁稳定性, 并且有效地调节费米能级处的自旋极化率(SP), 能在0—92% 之间变化, 这意味着可设计机械开关来控制低偏压下的自旋输运.应变调制机制与应变诱导的键长变化导致不成对的电子的重新分布或消失有关.这些纳米带的磁性主要来源于原子的p轨道, 这对于开发非过渡金属磁性材料有重要意义.