数学中考规律题的探究
仇阿会 赵临龙

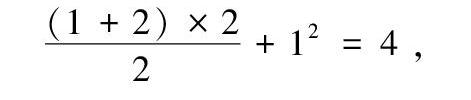
摘 要:近几年,中考试卷中出现规律题,此类题主要考察学生的思维能力和对数形结合的理解.本文通过对三道不同类型题的研究,给出寻找规律的一般解题思路。
关键词:中考;规律;研究
中图分类号:O175 文献标识码:A
通过观察近几年的中考题,发现规律题出现的概率越来越高。本文针对数式规律、几何规律、点的坐标规律等类型题型,进行解法研究。
1 探究数式规律题
数式规律题通常是给定一些数字、代数式、等式等,对其进行猜想所蕴含的规律。
解题一般思路是:先写出数式的结构,从前几项探索规律,通过归纳猜想,以及推理,给出其规律。
例1 请观察下列等式的规律:
11×3=121-13,13×5=1213-15,15×7=1215-17,17×9=1217-19,…则第nn1个怎么表示。 (2015湖南郴州改编) [1]
分析:观察题目所给的四个式子,发现等式左边分子是1,分母是两个数相乘,但第二个数总是比第一个数多2;等式右边都是12的两个相邻数的倒数的差,且是左边第一个分母的倒数减第二个分母的倒数。
解:11×3=11×(1+2)=121-11+2,13×5=13×(3+2)=1213-1(3+2),
15×7=15×(5+2)=1215-15+2,17×9=17×(7+2)=1217-17+2。
猜想第n个为:1n×(n+2)=121n-1n+2。
可以证明结论:
121n-1n+2=n+2-n2n×(n+2)=1n×(n+2)。
2 探究几何规律题
例2 图1都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有4个小圆圈,第 ②个图形中一共有10个小圆圈,第 ③个图形中一共有19个小圆圈,…,按此规律排列下去,第⑦个图形中小圆圈的个数是多少?第 n个图形呢?(2016重庆改编)[1]
分析:观察发现,图形由两部分组成:上部为三角形,下部分为正方形。于是可以通过做和,找规律。
解:第一个图形的小圆圈个数为4,其图形面积有关系:
(1+2)×22+12=4,
第二个图形的小圆圈个数为10,其图形面积有关系:
(1+3)×32+22=10,
第三个图形的小圆圈个数为19,其图形面积有关系:
(1+4)×42+32=19,
第四个图形的小圆圈个数为31,其图形面积有关系:
(1+5)×52+42=31。
………
即圖形的三角形和正方形边数依次增加数量1来递增面积。通过猜想,给出第n 个图形的小圆圈个数为:(1+(n+1))·(n+1)2+n2=(n+2)·(n+1)2+n2。
于是,第七个图形的小圆圈个数为(7+2)(7+1)2+72=85。
3 探究点的坐标规律题
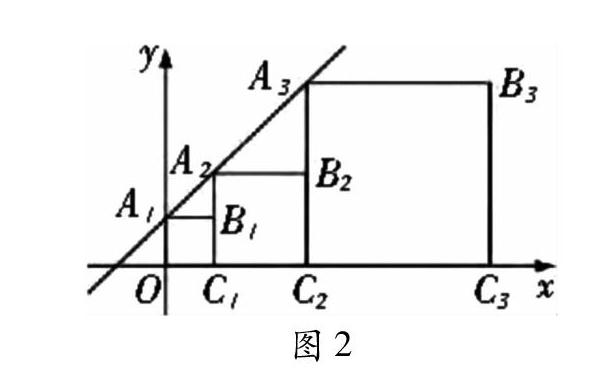
例3 如图2。正方形A1B1C1O, A2B2C2C1,A3B3C3C2,…,按如图2的方式放置。点A1, A2, A3, …和点C1, C2, C3, …,分别在直线y=x+1和x轴上,则点B6的坐标是? (2014孝感考题)[2]
分析:由图2知,点Bi(i=1,2,…)的坐标关系:横坐标值为前一点坐标的纵坐标值(由直线y=x+1得),纵坐标值为前一点坐标的纵坐标值。
解:因为直线y=x+1,当x=0时,y=1,则A1的坐标是(0,1);由于A1B1=1,点B1的坐标为(1,1),A2的坐标是(1,2);点B2的坐标为(3,2),A3的纵坐标是(3,4);点B3的坐标为(7,4),点A4的坐标为(7,8);点B4的坐标为(15,8),A5的纵坐标是(15,16);…。
此时,由点Ai(i=1,2,…)的坐标A1 0,1),A2(1,2),A3(3,4),A4(7,8),A5(15,16),得到:An(2n-1-1,2n-1)。于是Bn((2n-1-1)+( 2n-1+1),2n-1),即Bn(2n-1,2n-1)。
所以点B6的坐标为(26-1,25),即B6(63,32)。
4 小结
规律题看似复杂,但只要认真观察,找到方法,将会一击即中,不管哪种规律题,若能掌握方法,则可灵活解答。
参考文献:
[1]周春华.5年中考3年模拟中考数学 [M].安徽师范大学出版社,2017.
[2]生世忠.初中数学规律题的解题思想与方法例析[J].数学教学通讯,2014(34):62-64.

