结构动力响应数值计算方法对比分析

李涵

摘要：中心差分法、纽马克法、威尔逊-法是结构动力学中常用的三种方法，为了系统的比較其优缺性，本文针对一个双自由度的体系，首先根据已知条件计算出振动微分方程，运用Matlab计算出可求出12个步长内相应的位移值，即精确解。然后分别运用中心差分法，纽马克法，威尔逊-法求出其近似解;最后通过三种方法的近似解与精确解相对比，进而分析出三种计算方法的优缺性，为结构动力计算提供依据。

关键词：动力计算、中心差分法、纽马克法、威尔逊-法

1、动力体系概况

2、精确解推导

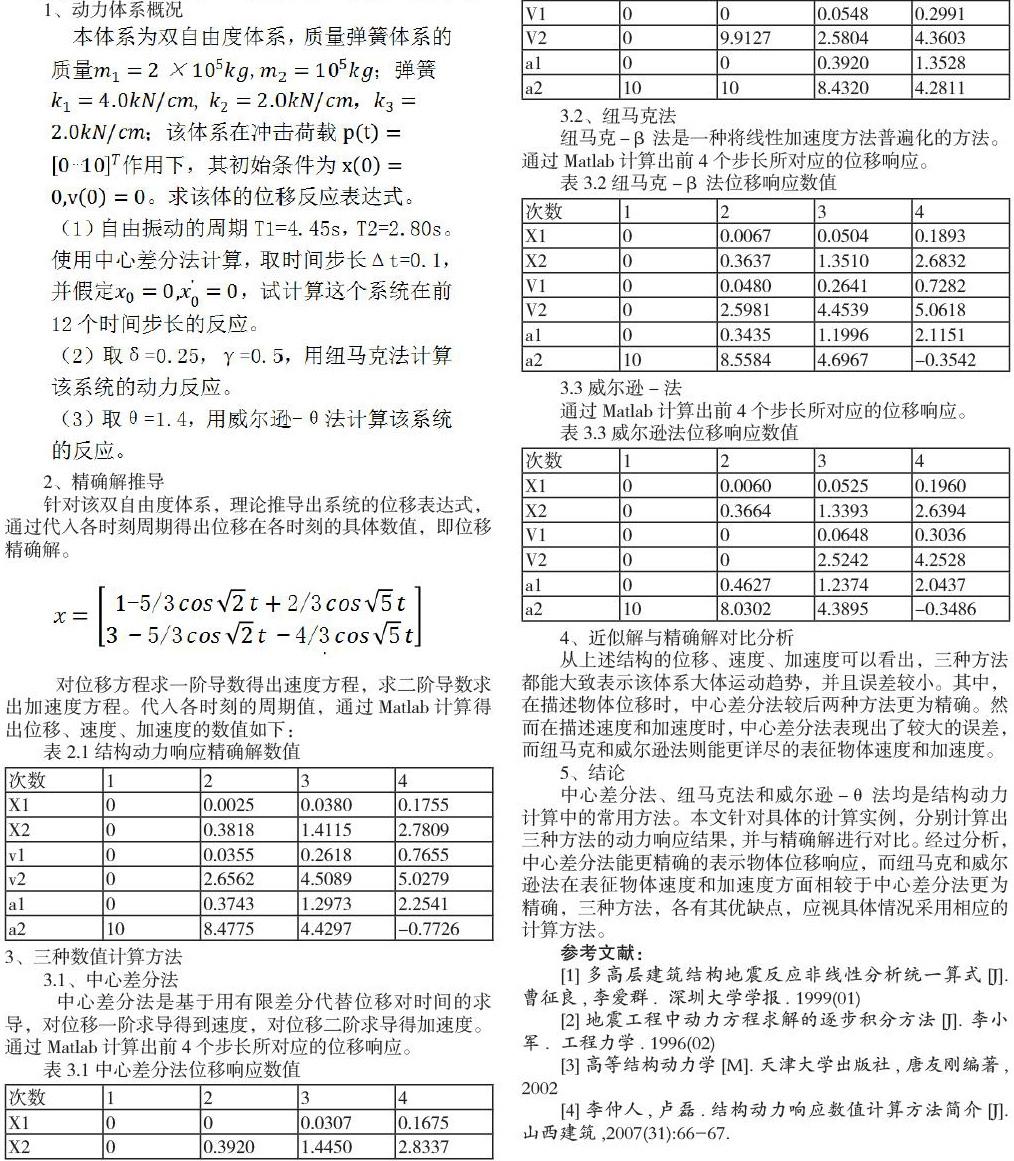
针对该双自由度体系，理论推导出系统的位移表达式，通过代入各时刻周期得出位移在各时刻的具体数值，即位移精确解。

对位移方程求一阶导数得出速度方程，求二阶导数求出加速度方程。代入各时刻的周期值，通过Matlab计算得出位移、速度、加速度的数值如下：

3、三种数值计算方法

3.1、中心差分法

中心差分法是基于用有限差分代替位移对时间的求导，对位移一阶求导得到速度，对位移二阶求导得加速度。通过Matlab计算出前4个步长所对应的位移响应。

3.2、纽马克法

纽马克-β法是一种将线性加速度方法普遍化的方法。通过Matlab计算出前4个步长所对应的位移响应。

3.3威尔逊-法

通过Matlab计算出前4个步长所对应的位移响应。

4、近似解与精确解对比分析

从上述结构的位移、速度、加速度可以看出，三种方法都能大致表示该体系大体运动趋势，并且误差较小。其中，在描述物体位移时，中心差分法较后两种方法更为精确。然而在描述速度和加速度时，中心差分法表现出了较大的误差，而纽马克和威尔逊法则能更详尽的表征物体速度和加速度。

5、结论

中心差分法、纽马克法和威尔逊-θ法均是结构动力计算中的常用方法。本文针对具体的计算实例，分别计算出三种方法的动力响应结果，并与精确解进行对比。经过分析，中心差分法能更精确的表示物体位移响应，而纽马克和威尔逊法在表征物体速度和加速度方面相较于中心差分法更为精确，三种方法，各有其优缺点，应视具体情况采用相应的计算方法。

参考文献：

[1]多高层建筑结构地震反应非线性分析统一算式[J]. 曹征良，李爱群.  深圳大学学报. 1999（01）

[2]地震工程中动力方程求解的逐步积分方法[J]. 李小军.  工程力学. 1996（02）

[3]高等结构动力学[M]. 天津大学出版社 ， 唐友刚编著， 2002

[4]李仲人，卢磊.结构动力响应数值计算方法简介[J].山西建筑，2007（31）：66-67.