基于遗传算法的钢水“脱氧合金化”成本优化研究

苏庆 周泓机 邹立志

摘 要：随着钢铁行业中高附加值钢种产量的不断提高，在保证钢铁质量的同时尽可能减少成本尤为重要。本文基于低碳钢HRB400B的历史数据记录，构建BP神经网络-脱氧合金化预测模型。根据16种合金原料的元素含量和单价，建立“脱氧合金化”总成本最优化模型，并采用遗传算法进行求解。结果显示，相同成本的不同方案中，各合金原料的用量可能存在较大差别，故应根据炼钢厂的实际情况确定合理的合金配料方案。

关键词：多元回归;BP神经网络;遗传算法;目标约束模型

中图分类号：TF769文献标识码：A文章编号：1003-5168（2019）16-0032-03

Abstract： With the continuous improvement of the output of high value-added steel in the iron and steel industry， it is particularly important to reduce the cost of steel while ensuring the quality as much as possible. Based on the historical data of HRB400B of low carbon steel， a BP neural network-deoxidization alloying prediction model was constructed in this paper. According to the element content and unit price of 16 kinds of alloy raw materials， the total cost optimization model of "deoxidization alloying" was established and solved by genetic algorithm. The results show that there may be great difference in the amount of alloy raw materials in different schemes with the same cost， so the reasonable alloy proportioning scheme should be determined according to the actual situation of the steelmaking plant.

Keywords： multiple regression;BP neural network;genetic algorithm; goal constraint model

随着对现代钢材质量要求的提高，对冶炼过程中加入合金的数量和种类要求也越来越精准。在炼钢产业中，合金收得率是炼钢设备工艺和技术操作的一个重要指标，即脱氧合金化过程中被钢水吸收的合金元素的重量与加入该元素总重量之比。C、Mn元素是钢材中两种最主要的元素。本文基于HRB400B低碳钢的炼钢历史数据、合金料成分说明及主要合金元素含量的国家标准，对现有的脱氧合金工艺进行优化分析，在满足合金元素含量要求的前提下，确定最佳的合金配料方案，以尽可能控制生产成本。

1 影响C、Mn收得率的主要因素

设钢水净重为M（kg），炉内钢水元素占比为a（%），合金加入总量为Mp（kg），合金中元素成分占比为b（%），合金元素收得率为[δ]（%），可得到合金加入后的元素成分占比为c（%）的表达式：

（1）

由于低合金钢合金元素含量低，合金加入量少，合金用量对钢液总质量的影响可以忽略。合金加入量的近似计算式为：

（2）

则合金历史收得率的近似表达式为：

（3）

1.1 C元素历史收得率的主要影响因素

将C元素历史收得率[δ]作为多元函数的函数值，所有影响因素作为多元变量[x1，x2，x3，…，xn]，[η1，η2，η3，…，ηn]分别是以上多元变量的影响因子，则多元方程为：

（5）

转炉终点温度、转炉终点以及硅钙碳脱氧剂等42个因子作为自变量xn，合金历史所得率作为因变量[δm]，利用MATLAB进行自动回归多次后，得到每个影响因素变量对应权重因子η的值。碳元素历史收得率影响因素的权重因子如表1所示。

C历史收得率的主要影响因素是转炉终点及连铸正样。为了验证线性相关性，计算相关系数R2=0.985 1，系數接近1，相关性较好。残差分析回归拟合出的所有点与实际数据的误差在0.4%左右，回归效果好。

1.2 Mn元素历史收得率的主要影响因素

Mn元素历史收得率的主要影响因素的分析方法与C元素相似。利用MATLAB自动回归多次后，得到每个影响因素变量对应的权重因子。相关系数R2=0.985 1，相关性好。进行残差分析后，回归拟合出的所有点与实际数据的误差在0.3%左右，结果较理想。Mn历史收得率影响因素的权重因子如表2所示。

2 C、Mn元素收得率的数学预测模型

BP神经网络，即反向传播神经网络，具有自学习、自组织和强鲁棒性的优点，能满足实际生产要求[1-3]。采用含有一个隐层的三层多输入单输出的BP网络建立预测模型。通过样本数据的训练，不断修正网络权值与阈值，使误差函数沿负梯度方向下降，逼近期望输出。

2.1 C元素收得率预测模型

2.1.1 输入输出层设计。该模型由每组数据的各项影响因素作为输入，以元素收得率作为输出，输入层的节点数为20，输出层的节点为1。

2.1.2 隐层设计。有一个隐层的神经网络，只要隐层节点足够多，就可以以任意精度逼近一个非线性函数。在选取隐层神经元的个数时，参照以下经验公式：

（6）

其中，e为输入层神经元个数;f为输出层神经元的个数;g为[4，10]之间的常数。根据上式计算出神经元的个数为9～15。取隐层神经元个数为9，利用MATLAB设计程序得到网络结构如图1所示。预测模型设定完参数后，开始训练。

2.1.3 结果。网络训练完成后，只需要将各项指标输入网络即可得到预测数据。预测值与实际值的R相关性如图2所示。从图2可知，预测值与实际值的吻合度较高，故BP神经网络的预测能力较好。

2.2 Mn元素收得率预测模型及结果

Mn元素收得率预测模型及训练步骤和C元素收得率的预测完全相同。网络训练完成后将各项指标输入网络得到预测数据，由BP神经网络R相关性分析可知：Mn元素收得率的预测值与实际值的变化规律相同，预测模型较准确。

3 基于遗传算法的钢水脱氧合金化成本优化模型

遗传算法是一种全局寻优算法，能从多个点构成的群体开始搜索，且不易陷入局部最优点。若用穷举法求解多约束非线性规划问题，算法空间较大;采用遗传算法，在满足标准的前提下，结合BP神经网络收得率预测模型对脱氧合金化成本进行优化，提高经济效益，并做到物尽其用。

3.1 决策变量

设合金化元素为i，需要合金化的元素为C和Mn，所以i=1，2，调整C和Mn含量的合金原料种类为[G1]种，[jmax=16]，每种合金的加入量[α1，α2，…，αj]是決策变量。

（7）

其中，决策变量非负。决策变量的两个自变量构成了二维欧几里得空间，二维空间中任一点对应一组合金添加方案，即[αii=1，2]。

3.2 目标函数

在保证达到钢种成分要求范围时，经济地进行转炉脱氧合金化操作，使钢水脱氧合金化成本最低，即

（8）

式中，[Z]为钢水脱氧合金化总成本;[kt]为第t种合金原料的价格。

3.3 约束条件

本题以低碳钢种，钢号为HRB400B的合金元素含量标准进行约束。

3.3.1 对C、Mn元素含量的约束。设[Pti]是第t种合金原料中元素[ii=1，2]的含量，[δi]为元素[i]的收得率，[αj]是合金原料j的加入量，M是钢水净重，则：

（9）

其中，[Li]、[Hi]分别为元素[i]含量内控区间的下限值和上限值。分式中分子表示元素[i]的重量，分母表示钢水的重量。

3.3.2 非负条件。加入钢水的16种合金原料的质量取值不可能为负值，只存在加和不加两种情况，所以：

（10）

3.4 合金优化计算数学模型求解

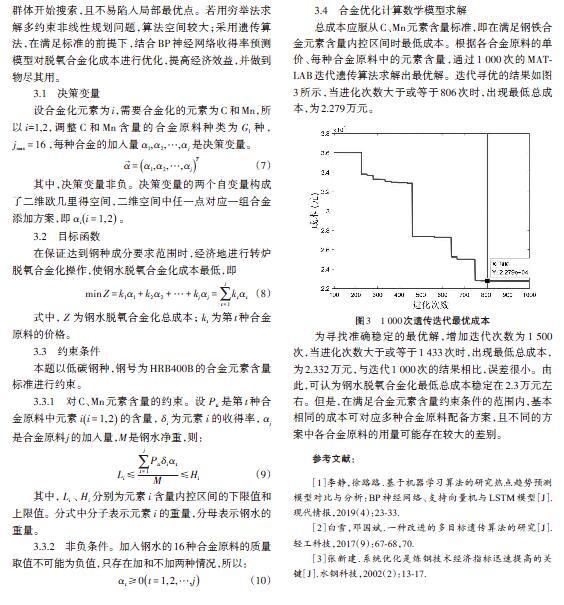
总成本应服从C、Mn元素含量标准，即在满足钢铁合金元素含量内控区间时最低成本。根据各合金原料的单价、每种合金原料中的元素含量，通过1 000次的MATLAB迭代遗传算法求解出最优解。迭代寻优的结果如图3所示，当进化次数大于或等于806次时，出现最低总成本，为2.279万元。

为寻找准确稳定的最优解，增加迭代次数为1 500次，当进化次数大于或等于1 433次时，出现最低总成本，为2.332万元，与迭代1 000次的结果相比，误差很小。由此，可认为钢水脱氧合金化最低总成本稳定在2.3万元左右。但是，在满足合金元素含量约束条件的范围内，基本相同的成本可对应多种合金原料配备方案，且不同的方案中各合金原料的用量可能存在较大的差别。

参考文献：

[1]李静，徐路路.基于机器学习算法的研究热点趋势预测模型对比与分析：BP神经网络、支持向量机与LSTM模型[J].现代情报，2019（4）：23-33.

[2]白雪，邓国斌.一种改进的多目标遗传算法的研究[J].轻工科技，2017（9）：67-68，70.

[3]张新建.系统优化是炼钢技术经济指标迅速提高的关键[J].水钢科技，2002（2）：13-17.