多电极血液流速仪励磁系统优化研究

赵宇洋 万东瑜 姚健 吴学礼

摘 要：为了实现对人体血液流量测量及流速分布的监测，基于多电极电磁测量设计了血液流速仪，通过测量皮肤表面的感应电动势，实现对动、静脉血液流速的测量。首先，模仿人体肢体结构，包括皮肤、脂肪、骨骼、肌肉、动脉和静脉的尺寸和相对位置，建立COMSOL仿真模型。然后，以赫姆霍兹线圈、C型铁芯线圈为基础，仿真研究了多种励磁结构和励磁方式在肢体测量截面处激励的电磁感应强度分布，提出了励磁线圈的优化设计方案，最后，对不同结构、不同激励方式的励磁系统进行了优化对比。结果表明，两对正交布置并且采用同向激励电流的赫姆霍兹线圈磁场呈中心对称，磁场强度和均匀性均优于其他励磁系统，能够有效增强感应电动势数值，更适用于非轴对称流的多电极电磁测量。研究结果验证了励磁系统优化方案的可行性，以及其均匀性对于提高速度重构精度的积极作用。

关键词：多相流动;区域权函数;励磁系统;多电极电磁;血液流速仪

中图分类号：TP391.9 文献标志码：A

文章编号：1008-1542（2019）04-0333-11

电磁流量计广泛应用于工业领域，如电力、石油化工、材料加工等，其工作原理为运动的导电液体受到磁场作用产生洛伦兹力，电荷受力聚集在边界处形成电动势，通过测量感应电动势便可计算流体的速度和流量。随着对电磁流量计的深入研究，其测量精度不断提高，类型多种多样，应用范围越来越广。CUSHING[1]改善信号传输受到的零点漂移影响，增强了流量信号传输效率。为了在信号测量时防止静电的干扰，AMARE[2]设计了两种新型电极。之后，张小章[3]、徐立军等[4]、王国强等[5]对电磁流量计流体速度场的重构作了深入研究。梁强等[6]设计了一套流速较低流体的测量方案。牛滨等[7]则在电磁信号提取与滤波方面进行了研究和实践。

研究结果和实际应用表明，两电极电磁流量计在测量轴对称流动时的精度较高，然而在实际测量中，流体的非轴对称性广泛存在且会导致严重的电磁测量系统误差。对此有研究人员提出用多电极方法来提高不对称流的测量精度。由于磁场强度和磁通密度的分布影响被测流体洛伦兹力的大小和方向，相同数目、相同布置方式的多电极传感器在不同励磁系统激励下测得的感应电动势不同，特别是当被测流体为非轴对称流动时磁场参数尤其重要。

本文采用非侵入式多电极电磁方法测量人体血管内方向互逆的动、静脉血流速度，励磁系统产生测量界面处所需的均匀磁场，安置在肢体表面的多电极拾取动、静脉感应电动势，通过区域权函数和速度重构方法可以实现对血液流动速度剖面的测量。笔者不仅发展了该方法的理论基础，而且通过有限元建模仿真和实流试验进行了验证。结果表明，多电极电磁血液流速仪在对心血管疾病的预测研究中具有重要意义并且可行[8]。医生可以通过实时监测患者在医院期间动、静脉血流的变化来确定术后的健康状况[9]，并及时采取相应措施。

1 模型构建和模拟方法

医学研究表明，血流速度测量是一种与人体器官或组织中氧气和营养物质的测量直接相关的方法，血压能反映出人体肢体的压力水平，但并不能提供关于输送到器官或组织的血液数量的定量信息。测量血流速度在循环系统和心脑血管疾病的研究中具有重要意义。如测量单个血管的血流速度可检测动脉是否狭窄——动脉狭窄导致组织血流减少，血流减少会产生各种病症[10]。

人体的血管大致可以分为动脉、静脉和毛细血管等几类，人体的血液黏度较高，为水黏度的4倍～5倍。动脉的功能是把心脏的血液输送到全身各处，静脉的功能是把全身各处的血液送回心脏，毛细血管连通最小动脉和最小静脉，是血液与组织细胞之间进行物质交换的场所。其中动脉的血管壁最厚，弹性大，管腔较小，血流速度最快，位于肢体较深的部位。静脉血管壁薄，弹性小，血流速度慢，位于肢体较浅部位。表1显示成人动脉（如主动脉、颈动脉、肱动脉、股动脉和腘动脉）的直径和峰值血流速度的典型值[11]。本文提出的电磁血流速度测量方法旨在测量上肢肱动脉和普通腓肠肌等外周动脉的血流速度。

由于人体血管分布特性及动、静脉逆向流动的特点，本文研究的血液流动对象为典型的非轴对称流体，当被测流体呈非轴对称时，流动情况复杂，速度剖面不规则。为保证多电极测量血液逆向流动的速度分布，励磁系统的优化对于多电极电磁测量尤其重要。本文提出了线圈优化方案和励磁参数优化，目的在于最大化边界电压测量的系数或最小化重建的速度场估计中的不确定性。结果表明，通过优化线圈磁場发生结构和激励电流的相位，有利于电磁测量获得准确的速度场估计值。

选用COMSOL Multiphysics多物理场仿真软件中的电磁模块展开研究，主要针对铁芯式线圈和无芯式线圈的励磁结构进行优化：一类为带有导磁铁芯的C型铁芯线圈;另一类为无芯式赫姆霍兹线圈。理论分析表明，线圈间隙过大时会产生明显的磁漏现象，空气间隙越大，磁漏越明显，电干扰越严重，所以为了减小磁漏、获得分布均匀且强度较高的磁场，在励磁结构设计时选用C型铁芯构成，既减小气隙又增加磁场均匀性。赫姆霍兹线圈是由英国物理学家赫尔曼·冯·赫姆霍兹发明的，由2个完全相同的圆形线圈组成，在2个线圈中通入相位和数值相同的电流，就会在2个圆形赫姆霍兹线圈的轴向平面处产生均匀磁场[12]。本文针对人体上肢动、静脉血液流速的测量进行研究，动、静脉血液的逆向流动、其他毛细血管和组织液的流动干扰，以及个体差异导致的上肢动、静脉血管的位置差异，都会影响测量进度[13]。为提高测量方法的精度和通用性，优化励磁系统、提高磁场强度和均匀度的研究十分有必要[14]。针对C型铁芯线圈和赫姆霍兹线圈进行结构优化和励磁参数优化，测量截面处产生磁场的均匀性和对称性，为以后的实验研究选择合适的励磁线圈和工作方式。

赫姆霍兹线圈是由2个彼此平行且连通的共轴圆形线圈组成，两线圈中的电流相位一致、大小相同时，在轴向平面处激励产生均匀磁场，而且产生的磁感应强度数值与线圈电流成正比[15]。此时所产生的总磁场为

C型铁芯线圈由导电铁芯和铁芯上的励磁线圈组成，其中线圈中的导线匝数、励磁电流的数值是影响磁感应大小的主要参数。文中通过实验验证了其在气隙处产生的磁场为均匀磁场，磁通量是由中心向外扩散的，即均匀磁场位于气隙的中心处范围内[16]。此时气隙处的磁场为

由于人体生物特征的个体差异性，手臂内的动、静脉血管位置存在差别，采用多电极电磁测量方法，通过区域权函数反映不同区域的流动对不同电极间感应电动势贡献大小，利用速度重构算法，可以有效避免流动位置差异对测量精度的影响。该方案中区域权函数是与传感器结构有关的无量纲量，当电极数目与分布方式确定时，系统测量精度仅由磁场强度和磁场均匀性决定。研究表明，对于多电极电磁测量，磁场分布的均匀性越好，非流动因素引入的测量误差越小。所以通过优化励磁线圈结构和激励方式来增加磁场的对称性与均匀性：首先研究C型铁芯线圈与无芯式赫姆霍兹线圈的励磁特点;其次，为了增加测量截面处的磁感应强度，增加线圈数量，组成2对赫姆霍兹线圈（HZ2线圈）与4对赫姆霍兹线圈（HZ4线圈）的励磁结构，并采用不同激励方式，图1为4种励磁系统的结构示意图。

如图1所示，为了使模型更加符合人体手臂，根据国际人体手臂标准参数，模拟肢体的几何圆柱体设置为半径30 mm，内层圆设置为半径27 mm以模拟肌肉层，之间设置为皮肤脂肪层。动脉血管半径设置为5 mm，模拟动脉血流方向为垂直纸面向外，速度设置为0.6 m/s，骨骼组织半径为8 mm，静脉血管设置为半径为5 mm的圆，里面通垂直纸面向内的血液，速度为0.2 m/s。剩余部分设置成肌肉与毛细血管组织。

针对不同结构的励磁系统和励磁方式进行研究，表2为励磁系统的符号含义。

2 励磁系统优化对比

为了对比文中不同结构、不同激励方式下励磁系统产生的磁场强度与均匀性，统一将线圈激励电流大小设置为2 A，线圈匝数为5 000 匝，求解域设置安培定律与电流守恒，设置完边界条件后分别模拟不同线圈所产生的磁场并进行比较，如图2所示。图中C型铁芯线圈电流方向沿y轴向上，为了产生方向相同的磁场，将赫姆霍兹线圈激励电流设置为同向的2 A电流。

启动仿真并进行后处理。C型铁芯线圈和无芯式赫姆霍兹线圈在测量截面处激励产生的磁场如图3所示。

通过分析，图3中两种结构的励磁系统在被测管道横截面处感应磁场的平均数值相对误差小于5%，均匀性也较好。此外，两线圈均在y轴方向上出现感应磁场极小值，在x轴方向处有感应磁场极大值，量化计算表明磁场值的波动比较小，管道内磁场关于y轴对称，所以在整个测量截面可以视作近似均匀的磁场。对比表明，C型铁芯线圈产生的磁场要比赫姆霍兹线圈磁场强9.3%左右，赫姆霍兹线圈在同样激励条件下磁场均匀性更好。

分析表明，C型铁芯线圈和赫姆霍兹线圈在测量横截面处的磁场呈现轴对称性，如果被测对象的动、静脉血液流动主要沿y轴方向发生偏移时会产生较大的测量误差，所以考虑对称增加赫姆霍兹线圈的对数以提高磁场的对称性与均匀性，励磁系统结构如图4所示。

针对两对赫姆霍兹线圈正交布置的励磁结构，沿yz平面对称的两线圈C4-1和C4-4以正向2 A电流激励（记作HZ2-P线圈），沿xz平面对称的C4-1与C4-3线圈以反向电流激励（HZ2-N线圈），根据相同条件设置求解域和边界条件，励磁系统仿真结果如图5所示。

根据图5可知，HZ2线圈产生的磁场呈中心对称，对称性比C型铁芯线圈和赫姆霍兹线圈的轴对称要好。而在均匀度上，HZ2-P线圈得到两条交叉的电磁下降区域，HZ2-N线圈则是相对产生的磁场在圆心处下降很快。磁场强度则是HZ2-N线圈比HZ2-P线圈强20.47%左右。

最后将励磁系统的线圈数量增加到4对。4对赫姆霍兹线圈沿xy平面45°均匀分布，

观察磁场强度和对称性是否有较大改善，励磁系统结构如图6所示。

HZ4线圈也分为2种情况。第1种情况是两相邻线圈为1组，同组2个线圈同向电流激励，相邻两组线圈反向电流激励，即C8-1～C8-2 与C8-5～C8-6设定为2 A的电流，C8-3～C8-4 与C8-3～C8-4设定为-2 A的电流，得到的励磁系统命名为HZ4-P线圈。第2种情况是相邻线圈的激励电流两两反向，即C8-1设定为正向2 A的电流激励，C8-2线圈以-2 A电流激励，C8-3再以2 A电流激励，以此类推得到的励磁系统命名为HZ4-N线圈。根据相同条件设置求解域和边界条件，励磁系统仿真结果如图7所示。

根據图7可知，HZ4线圈产生的磁场对称性也属于中心对称，HZ4-P线圈与HZ4-N线圈产生了中间八角形的磁场下降区域。所以HZ4线圈通入电流方向的情况对磁场强度影响不大，但电流方向会影响感应磁场的方向，所以在磁场方向上两种情况还是会有较大的不同。

为量化比较6种磁场的均匀程度，通过测量管道内圆心划出8条半径线，每条半径上等距截取5个点，半径间夹角45°，总共截取40个点分别测量磁场的大小，如图8所示。

以HZ2-N线圈产生的磁场为例，列举在被测管道内截取的40个点的位置上磁场强度的值，如表3所示。表3纵列为选取的半径与3点钟方向的半径之间的夹角度数，行向是由被测管道的圆心向管壁所选取的5个点，构成5×8的表格，总共40个点的磁场强度。

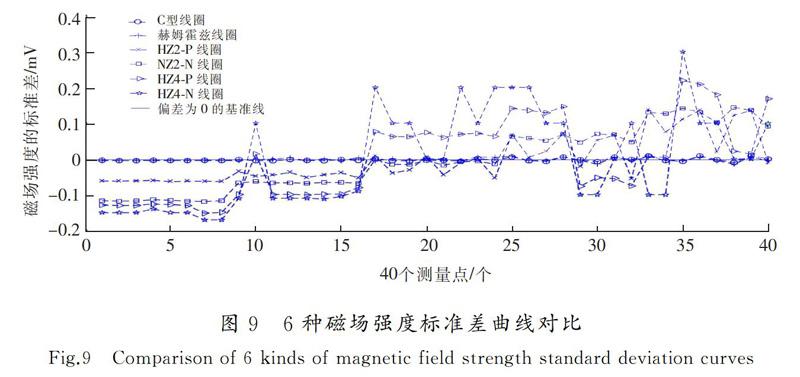
为了更加直观地比较6种励磁系统产生磁场的均匀度，使用MATLAB软件将6种磁场分别在40个点的位置得到了40个磁场强度后可以求出磁场的平均值，再将40个点的磁场强度分别减去平均值得到标准差，将40个标准差连接的曲线与标准差为0的基准线相比较，如图9所示。

根据图9可知，C型铁芯线圈与赫姆霍兹线圈的磁场波动程度最小。而HZ2线圈在半径6 mm的内圆里磁场较弱，因此在平均值以下。在半径为6～30 mm时磁场数值则在平均值上下波动，因为手臂血管分布在手臂半径8～27 mm左右，所以对测量结果不会产生太大影响。HZ4线圈因为产生磁场的线圈过多，导致磁场方向与强度分布复杂，所以曲线波动很大，会影响血流的测量。

当在这两种感应磁场中设置被测流体为动、静脉的血液流动时（动脉血0.6 m/s，静脉血-0.2 m/s）产生如图10所示的感应电压分布。

根据图10可知，随着磁场的增强，感应电压的强度也随之增大，而二者均匀度相差不多，所以感应电压的分布基本一致。

然后对HZ2线圈的两种情况设置相同的动、静脉的血流时（动脉血0.6 m/s，静脉血-0.2 m/s）产生如图11所示的感应电压分布。

根据图11可知，感应电压较之前的两种情况增强了15%，但由于HZ2-P线圈的磁场相较于赫姆霍兹线圈的情况变得更为复杂，所以得到的电场也发生了偏转，而偏转严重会给测量后的16点电压反推血液流速带来一定干扰，HZ2-N线圈则由于自身良好的对称性并没有偏转。

对HZ4线圈的两种情况设置相同的动、静脉的血流时（动脉血0.6 m/s，静脉血-0.2 m/s）产生如图12的感应电压分布。

根据图12可知，电场随磁场得到了进一步增强，但由于内部磁场方向变得更为复杂，所以对应电场偏转更为严重，而偏转严重会给测量后的16点电压反推血液流速带来一定干扰。

3 多电极区域权函数测量机理

多电极电磁流速仪的优点在于可以从被测管道的绝缘管壁处在不同的角度或者不同位置来测量被测管道绝缘壁上的感应电动势，得到了被测流体在被测管道不同位置感应电动势信息，就能够精确测得复杂流体的情况。被测管壁上布置的电极数目越多，得到的感应电动势的值越详尽，因为重构算法需要组成方阵，对应地就要将被测管道横截面的区域划分得更详细，从而重构出的管道流速信息就更为精确。根据研究，当电极数目≥16时，由一般的非轴对称流得到的速度误差估计不大于0.3%，属于系统误差范围，其对流速测量的影响可以忽略不计。虽然电极数目越多速度重构的精度越高，但是电极数目增加到一定数量时，会带来巨大的技术难度，而且随着电极数目的增多，加工费用会呈现几何级的增大，还会使测量系统的信噪比增大、感应电压信号的收集难度增大等，所以需要在测量精度足够的前提下，考虑方案的可行性、信号的收集处理难度、经济效益等，并增加电极数目。在Shercliff权函数的理论基础上[17]，针对测量截面不同位置流体的平均流速，本文采用了區域权函数算法。

综上所述，对比了电极数目和区域划分方式对被测流体速度重构的影响，采用16电极的多电极电磁血液流速仪进行仿真[18]。如图13所示为多电极电磁流量计示意图。

本小节介绍了多电极电磁流量计的流体流速测量机理，着重描述了基于Shercliff权函数推导得到的区域权函数[21]，对于区域权函数总结得出以下几点：

1） 工业生产与生活中被测流体的情况多为复杂流体，所以在被测量管道的横截面中不同的区域内对每个电极求得的权函数大小会各不相同;

2）传统电磁流量计因其技术的局限只能测量被测量流体为轴对称流的流动;

3）多电极电磁流量计对被测流体的测量相对广泛，即结合权函数理论可以测量被测流体非轴对称流动，并经过速度重构算法得到各区域平均速度。

综上所述，多电极电磁流量计可获得多相流平均液体速度，是非侵入式测量多相流的有效工具，适合各种管道和容器使用和各种多相流测量领域。依据区域权函数理论可以针对各区域的速度计算得到各区域对电极对的贡献，减少了对被测流体的条件要求，为后面人体肢体血液流速的测量提供了理论基础。

4 仿真实验结果

为了更加直观地比较6种励磁系统的均匀性对血液测量的影响，根据区域权函数理论先计算16电极传感器针对动、静脉血液测量的权函数数值，再用被测管道周边的16个电极测得16个感应电压的数据，用均匀磁场测得感应电压为标准值，将6种励磁系统测得的感应电压与之对比，7种磁场所得的16个电压数据如图14所示。

根据式（6）可以求出当磁场均匀时，得到的16点电压是一条接近正弦的曲线。如图14可以看出，HZ4-P线圈和HZ4-N线圈因为电磁铁繁多，所以造成了测量管道内磁场复杂，导致测得的16点电压偏离正弦波波形，而且电压最大值与最小值之差保持稳定。C型铁芯线圈、赫姆霍兹线圈、HZ2-P线圈、HZ2-N线圈都构成了比较接近正弦波曲线的波形且电压最大值与最小值相差明显，同时最接近于计算得到的数据。

最后将仿真模型动、静脉血液流动分别设置为血液流速的正常平均值0.6 m/s和-0.2 m/s，仿真得到肢体表面16电极处的感应电动势，再根据区域权函数值，使用速度重构MATLAB算法对人体肢体血管模型仿真进行计算，得到如图15所示的血流速度重构图。

模拟对比了6种情况下励磁系统所产生的磁场。在MATLAB中，使用16电极来测量由线圈产生的磁场激励得到的感应边界电压。使用基于权函数的计算方法和针对求逆矩阵方法，基于测量的边界电压重建速度场。其中将HZ2线圈和HZ4线圈的位置设置为固定位置，并且对相同的线圈数量采用不同的电流方向来产生不同的磁场。结果表明，通过对非对称流动仅使用1个或2个最佳磁场，可以获得准确的速度场估计。C型铁芯线圈和赫姆霍兹线圈产生了比较强的轴对称磁场，而HZ2线圈产生的磁场呈中心对称，HZ2-P线圈得到两条交叉的电磁下降区域。HZ2-N线圈产生的磁场在圆心处数值下降得很快。HZ2-N线圈的磁场强度比HZ2-P线圈强20.47%左右，但所测血管分布在中心区域以外，对仿真结果影响不大。 HZ4线圈产生了最为均匀的磁场，但磁场内部流动最为复杂，其16点电压与计算结果的对比和血液速度重构与实际有较大误差，不适合应用于血液测量。综上所述，HZ2-N线圈与其他励磁系统相比，具有均匀性更好、产生的磁场呈中心对称、磁场强度更强、测量得到的16点电压更接近理论值等优点，更适合作为多电极血液流速仪的励磁系统。

5 结 语

1）针对血液测量中被测对象的个体差异性进行COMSOL Multiphysics仿真研究，结果表明16电极均匀布置的多电极电磁流量计能够有效测量肢体中各个位置的平均流速，避免血管位置和尺寸不同引入的测量误差。

2）采用MATLAB软件，通过提取COMSOL仿真模型的数据比较了6种不同结构、不同激励方式的励磁系统所产生磁场的均匀度及对称性，根据速度分布重构结果，提出了血液测量励磁系统应采用两对赫姆霍兹线圈正交布置，并采用反向电流激励方式。

3）本文未对有关多电极电磁血液流速测量的各相平均流速求取算法进行研究，今后将对此进行进一步的探索。

参考文献/References：

[1] CUSHING V. Electromagnetic flowmeter for insulating liquids[C]// 19th IEEE Instrumentation & Measurement Technology Conference. Anchorage： [s.n.]， 2002：103-108.

[2]  AMARE T. Design of an electromagnetic flowmeter for insulating liquids[J]. Measurement Science & Technology， 1999， 10（8）：755-758.

[3]  张小章. 基于流动电磁测量理论的流场重建[J].计量学报，1998，19（1）：39-43.

ZHANG Xiaozhang. Flow pattern reconstruction based on the theory of electromagnetic flow measurement[J]. ACTA Metrologica Sinica， 1998，19（1）：39-43.

[4]  徐立军， 王亚， 董峰， 等. 基于多电极电磁流量计的流速场重建[J]. 自然科学进展， 2002， 12（5）： 524-528.

[5]  王國强， 吕波， 张小章. 非对称流动对电磁流量计输出的影响[J]. 计量技术， 2003（10）： 3-5.

[6]  梁强， 张宏建. 基于流型的文丘里管二相流量测量方法[J]. 化学工程， 2008， 36（7）： 20-23.

LIANG Qiang， ZHANG Hongjian. Measurement of two-phase flow rate with Venturi tube based on flow pattern[J]. Chemical Engineering， 2008， 36（7）： 20-23.

[7]  牛滨，陈松景，庞兵，等. 窄带滤波微流量电磁流量计的相关技术[J]. 哈尔滨工业大学学报， 2009，41（5）： 148-151.

NIU Bin， CHEN Songjing， PANG Bing， et al. Related technologies of narrowband filter low-velocity flow electromagnetic flowmeter[J]. Journal of Harbin Institute of Technology， 2009， 41（5）： 148-151.

[8]  唐飞， 王晓浩， 王东生. 热扩散法测量血液流速[J]. 仪器仪表学报， 2008， 29（5）： 978-981.

TANG Fei， WANG Xiaohao， WANG Dongsheng. Blood flow rate measurements using thermal diffusion[J]. Chinese Journal of Scientific Instrument， 2008， 29（5）： 978-981.

[9]  石丽英， 王友云. 血流速度绝对值的几种超声多普勒测量方法[J]. 北京生物医学工程， 1993， 12（1）： 19-24.

[10] 吴运平， 陈立波， 董家明. 现代血流测量方法[J]. 现代物理知识. 2004， 16（6）： 19-21.

[11] 李坤成， 杜祥颖. 应用磁共振进行血流测量的现状[J]. 中国医学影像技术， 1997， 13（5）： 463-468.

[12]  LEEUNGCULATION T， LUCAS G P. Measurement of velocity profiles in multiphase flow using a multi-electrode electromagnetic flow meter[J]. Flow Measurement and Instrumentation， 2013， 31： 86-95.

[13] YANG Y，WANG D，NIU P，et al. Measurement of vertical gas-liquid two-phase flow by electromagnetic flowmeter and image processing based on the phase-isolation[J].Experimental Thermal and Fluid Science，2019，101：87-100.

[14] SHERCLIFF J A. The Theory of Electromagnetic Flow-Measurement[M]. Cambridge： Cambridge University Press，1962.

[15]  PARALIEV M， GOUGH C， IVKOVIC S， et al. Eddy current focusing solenoid[J]. Nuclear Instruments and Methods in Physics Research A， 2011，637（1）： 12-17.

[16]  匡沙沙. 電磁流量计的基本原理及其特点[J]. 企业导报， 2010（11）： 284.

[17] ZHAO Y Y， LUCAS G， LEEUNGCULSATION T. Measurement and control systems for an imaging electro-magnetic flow meter[J]. ISA Transactions， 2014，53（2）： 423-432.

[18] HORNERB B， MESCH F， TRACHTLE A. A multi-sensor induction flowmeter reducing errors due to non-axisymmetric flow profiles[J]. Measurement Science Technology， 1996， 7（3）： 354-360.

[19] WANG J Z， TIAN G Y， LUCAS G P. Relationship between velocity profile and distribution of induced potential for an electromagnetic flow meter[J]. Flow Measurement and Instrumentation， 2007，18（2）： 99-105.

[20] 赵宇洋，姚健，万东瑜，等.多电极电磁流量计肢体血液流速分布测量研究[J].河北科技大学学报，2019，40（1）：60-66.

ZHAO Yuyang，YAO Jian，WAN Dongyu， et al. Measurement mechanism study of limb blood vessel velocity profile based on multi-electrode electromagnetic flow meter[J]. Journal of Hebei University of Science and Technology， 2019，40（1）：60-66.

[21] TARANTOLA A . Inverse Problem Theory and Methods for Model Parameter Estimation[M]. Auckland：Society for Industrial and Applied Mathematics， 2004.