基于成像测井的裂缝智能识别新方法

李冰涛,王志章,孔垂显,蒋庆平,王伟方,雷祥辉

(1.中国石油大学(北京),北京100000;2.中国石油新疆油田分公司勘探开发研究院,新疆克拉玛依834000)

0 引 言

裂缝是岩石中由于构造变形或物理成岩作用形成的面状不连续体[1]。在所有测井资料中,成像测井资料是最直接有效的裂缝识别资料。传统的裂缝识别基于人机交互的手工拾取,费时费力,因此,近年来成像测井裂缝自动识别一直是比较热门的课题,其中重要的一步就是图像分割,然而目前常用的图像分割算法均不够精确。为了得到最准确的图像分割结果,本文采用了图像分割算法,Google DeepLabv3+[2],对新疆油田车471井区成像测井数据,进行了裂缝的识别,并用改进的霍夫变换实现了裂缝产状的自动提取。

1 研究现状

成像测井资料地质现象定性描述方面的研究较多[3-8],但这类研究对地质现象的识别目前主要是依靠人工解释识别,效率低下。而成像测井资料的地质现象自动识别方面研究较少。杨绪海等[9]提出有效提取条纹背景噪声的算法模型,实现了岩石裂缝特征的自动识别;薛国新等[10]提出一种基于多数投票规则的裂缝计算机自动识别方法;陆敬安等[11]提出用霍夫变换来自动识别成像测井中的裂缝;李茂兵等[12]将裂缝分3种进行识别,即斜交缝利用霍夫变换来识别,垂直缝和水平缝利用轮廓跟踪和提取的方法来识别;王敏[13]提出基于小波多尺度分析和去噪的剩余曲线变化率进行裂缝识别,赖富强[14]提出改进的霍夫变换自动识别裂缝;张晓峰等[15]提出利用垂向的和横向的小波变换组合识别裂缝;张程恩等[16]提出基于蚁群聚类算法的成像测井裂缝识别;张群会等[17]通过免疫规则建立了一个基于元胞自动机模型的成像测井裂缝自动识别模型;刘英明等[18]年提出成像测井图像呈正弦地质构造自动拾取方法,刘文斌等[19]利用分水岭算法对成像测井裂缝进行图像分割,然后利用霍夫变换拾取裂缝参数。

上述方法要么没有提取出裂缝区域,仅通过统计特征确定裂缝的存在;要么利用图像分割提取出裂缝区域但不够准确,对下一步的参数提取造成影响。本文利用目前最先进的基于深度学习的DeepLabv3+卷积神经网络结构,对裂缝区域进行了准确提取,并采用霍夫变换对裂缝参数进行提取。

2 研究方法

2.1 语义分割

电成像测井裂缝自动识别一直是比较热门的课题,其中重要的一步就是图像分割。

常规图像分类的深度卷积神经网络,以图像作为输入,通过卷积、激活函数、池化和全连接层的运算,输出一个包含每个类别标签的概率的特征向量,代表图像类别。

与图像分类不同,语义分割对图像中的每一个像素作出分类。然而,常规卷积神经网络并不适用于密集预测的任务。首先,这些模型包含许多用于减小输入特征的空间维度的层,最终产生缺乏清晰细节的高度抽象的特征向量。其次,全连接层在计算过程中具有固定的输入规模和松散的空间信息。

因此,目前图像分割模型一般采用编码器解码器结构(见图1)。第1部分将信息编码为压缩向量来代表输入,第2部分解码器的作用是将这个信号重建为期望的输出。

2.2 Google DeepLabv3+

DeepLab是Google公司于2015年提出的语义分割模型,其第4个版本DeepLabV3+于2018年提出并在3月13日开源,在Pascal VOC 2012和Cityscapes上取得了极好的效果。

DeepLabv3+借鉴了PSPNet[20]中的空间金字塔池化模型(SPP),和基于全卷积神经网络的编码解码器模型[21-22]。DeepLabV3+进一步利用Xception模块[23],将深度可分卷积结构(depthwise separable convolution)用到带孔空间金字塔池化(ASPP)模块和解码模块中,得到更快速有效的编码解码网络(见图2)。由此不仅可以利用ASPP多样的感受视野有效提取图像多尺度的上下文信息,并且在新的解码器模块中加入了编码器中低层次网络的特征,以重构精确的图像物体边界。

DeepLabv3+使用了其前一代模型DeepLabv3作为编码器,其使用ASPP来提取不同尺度的卷积特征,而后在解码器模块中首先将编码特征采用因子4进行双线性上采样,然后连接从主干网络所输出的对应的具有相同空间分辨率的low-level特征,连接后采用3×3的卷积核和因子4的双线性上采样来改善特征。

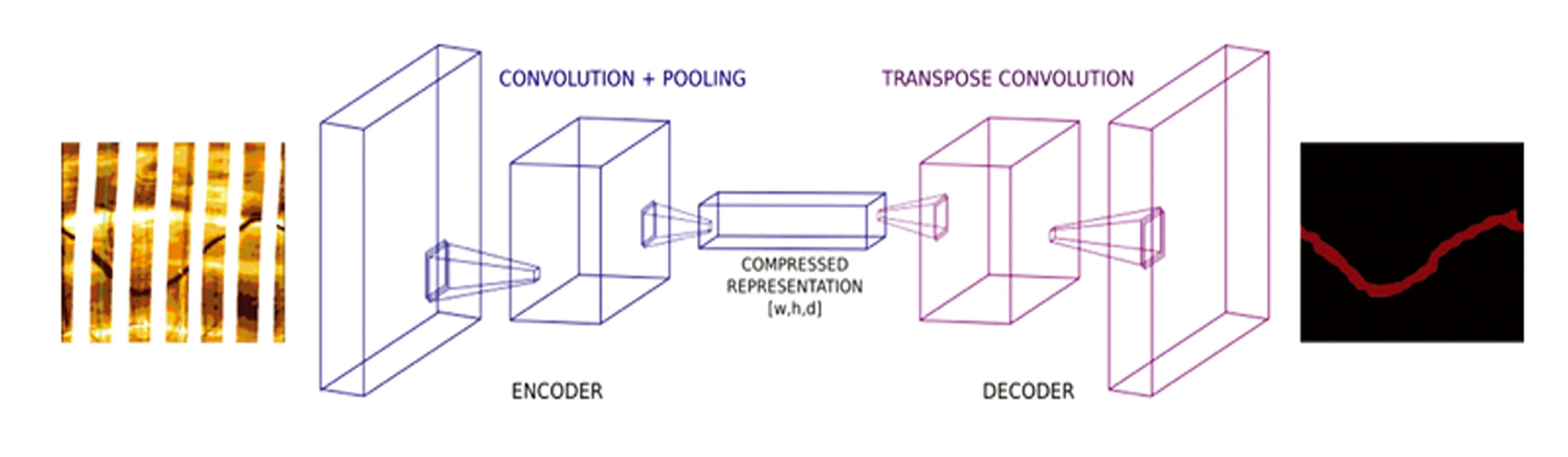
图1 用于图像语义分割的编码器解码器结构

图2 编码解码网络

图3 DeepLabv3+整体架构(Chen et al.2018)

2.3 霍夫变换提取正弦曲线

霍夫变换[24]最初用来检测直线,后来拓展到可以识别和检测图像空间的任意解析曲线。霍夫变换的原理是将特定图形上的点变换到一组参数空间上,根据参数空间点的累计结果找到一个极大值对应的解,那么这个解就对应着要寻找的几何形状的参数。

由于正弦曲线y=Asin (ωx-φ)+y0中共有4个参数,其参数空间为4维,对应的霍夫变换计算量过于庞大,因此本文参考了邹长春等[25]改进的霍夫变换快速检测方法:首先,由于成像测井裂缝正弦曲线周期始终为图像宽度,可确定参数ω。之后,再利用正弦曲线上半周期距离的2个点的中点的纵坐标为其基线的位置这个性质,利用与霍夫变换类似的多数投票机制,确定基线的位置,从而确定参数y(见图4)。

图4 确定正弦曲线基线位置y0的示意图

如此,正弦曲线仅余2个参数待确定,此时再利用霍夫变换,求取振幅A和初相位φ。仅由A和φ建立霍夫变换参数空间,计算量大大减小。

3 实验结果及讨论

3.1 数据集

利用labelme开源工具,对新疆车47井区的成像测井图像进行裂缝区域的标定,得到300张标注过的图片,尺寸为286×278。之后选取240张图片,输入DeepLavbv3+模型进行训练,剩余60张作为测试数据。

3.2 评价指标

图像分割中通常使用许多标准来衡量算法的精度,通常是像素精度及IoU的变种,在众多度量标准中,由于MIoU简洁、代表性强,文中采用均交并比作为评价标准[26]。

均交并比(Mean Intersection over Union MIoU):语义分割的标准度量。计算2个集合的交集和并集之比,在语义分割的问题中,这2个集合为真实值和预测值。这个比例可变形为正真数比上真正、假负、假正(并集)之和。在每个类上计算IoU,之后平均。

(1)

式中,假设共有k+1个类(从L0到Lk,其中包含个空类或背景);pij表示本属于类i但被预测为类j的像素数量。即,pii表示真正数,而pij,pji则分别为假正和假负。

3.3 DeepLabv3+提取裂缝

本文的Deeplabv3+模型使用TernsorFlow在Python3.6上搭建。同时使用指标MIoU进行性能评估。模型采用5个样本的小批量进行训练,以模型收敛更加稳定。学习率从0.0001开始,并在整个培训过程中自动调整。训练过程见图5。最终模型在测试集上的MIoU达到83.2%,与Google用DeepLabv3+在Pascal VOC 2012数据集上得到目前所有模型最高84.56%的均交并比[2]相比,可认为是一个较为理想的结果。

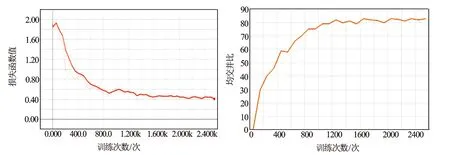
图5 损失函数值和均交并比随训练次数的变化曲线

图6 DeepLabv3+模型预测结果(左侧为成像测井原图,右侧为预测结果,红色为分割出的裂缝区域)

保存测试集中MIoU最高的训练模型对测试集成像测井图像进行语义分割,其结果见图6。图6左侧为成像测井原图,右侧为预测结果,红色为分割出的裂缝区域。与简单的图像二值化,以及流行的的图像分割方法如分水岭算法[27]、Chan-Vese算法[28-30]、Random walker算法[31]和Morphological Snakes算法[32]相比,该模型可更准确地预测裂缝所造成的正弦曲线形状的真实分布,即使不同极板之间图像数据的空白部分,依然可以预测出连续裂缝区域,得到更加准确的图像分割结果。此外,训练出的模型相比传统图像分割也能够准确忽略掉图像中非裂缝黑色像素的噪音影响,相比传统图像分割,该模型具有更强的鲁棒性。更准确的预测结果和排除噪音的影响,可以为下一步的霍夫变换减少计算量,并使其结果更加准确。

3.4 霍夫变换提取裂缝参数

利用霍夫变换求出裂缝的正弦曲线表达式之后,根据正弦曲线与裂缝的对应关系,裂缝倾向为正弦曲线y=Asin (ωx-φ)+y0中初相位φ对应的角度,可以通过下式获得其余裂缝参数

(2)

式中,H为裂缝的高度;A为振幅;mHeight为图像的像素高度;Dtop-bottom是成像图对应的深度区间(文中为1 m);α为裂缝倾角;D为井眼直径。对预测结果进行霍夫变换,提取的正弦曲线见图8,其参数见表1。表1中序号对应图8中序号。

图7 不同图像分割算法效果对比图

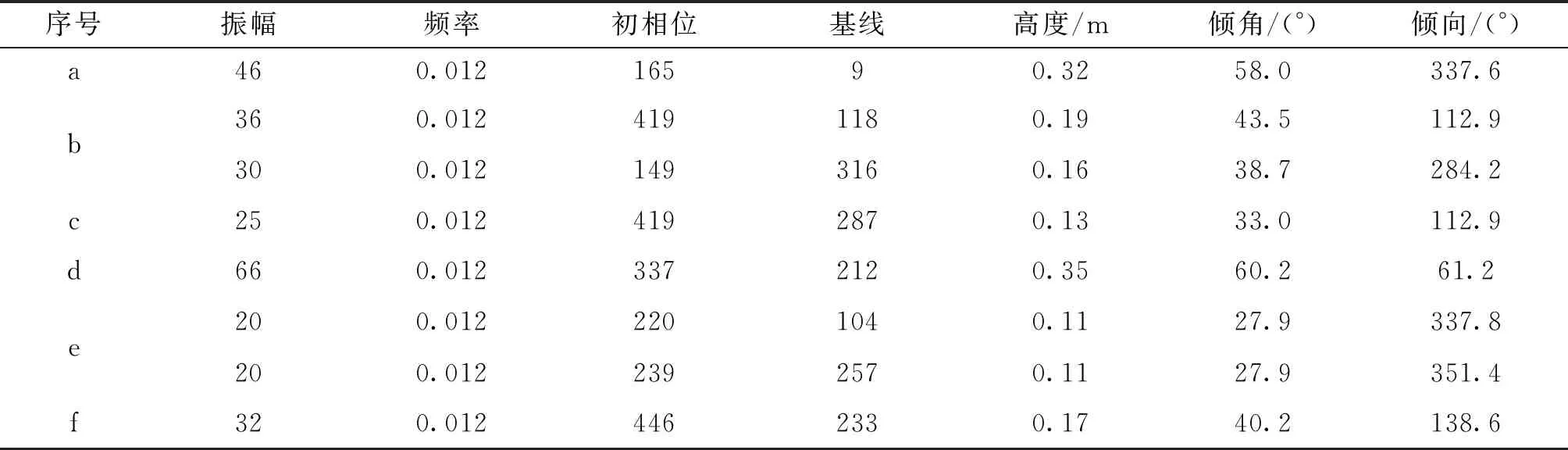
序号振幅频率初相位基线高度/m倾角/(°)倾向/(°)a460.01216590.3258.0337.6b360.0124191180.1943.5112.9300.0121493160.1638.7284.2c250.0124192870.1333.0112.9d660.0123372120.3560.261.2e200.0122201040.1127.9337.8200.0122392570.1127.9351.4f320.0124462330.1740.2138.6

4 结 论

利用DeepLabv3+模型进行成像测井裂缝的智能提取方法,相比传统图像分割方法,能够准确地对裂缝区域的像素进行分割;而且模型训练好之后对新的图像进行预测操作简便,速度快,降低人力成本;此外,能够为之后的霍夫变换减少噪音影响,从而加速霍夫变换计算速度,并使其提取的参数更加准确。